以核心概念為“源” 讓生命自然成長

作者簡介：劉俊岐（1982—），本科學歷，中學一級教師，從事初中數學教學與研究工作.

[摘 要] 數學核心概念是數學概念的主體與核心，它是一般數學概念的生長點和延伸點，正確理解核心概念有利于學生知識體系的建構和數學學習能力的提升. 教學中，教師要重視數學核心概念的整體性、生長性、思維性，為學生創設一個具有明確指向性的問題環境，引導學生經歷概念形成、發展及應用的過程，讓學生深刻理解概念的同時，實現知識、方法、經驗和思維的自然生長，體驗生命成長.

[關鍵詞] 數學核心概念;自然生長;生命成長

生長型核心概念教學的內涵

在數學概念體系中，有些概念處于核心地位，其他概念或是在其基礎上生成的，或是與之有著密切的聯系，我們常常將具有以上特征的概念稱為核心概念. 例如我們熟悉的平行四邊形，在平行四邊形概念的基礎上演變出了矩形、菱形、正方形等，構成了平行四邊形知識結構體系.

在生長型核心概念教學中，教師不應局限于單一概念的教學，應重視概念之間的內在聯系，引導學生經歷概念形成、發展和應用的過程，讓學生深刻地理解概念的內涵與外延，建構概念組織網絡和知識結構，以此通過知識與思維的再生長，助力學生自主學習能力和思維能力的提升.

生長型核心概念教學的特征

1. 整體性

數學知識不是孤立存在的，數學概念作為建構知識體系的核心，與其他概念有著密切的聯系. 核心概念是一般概念的“源”，教學中應以“源”為抓手，引導學生從上位概念、本位概念、下位概念等多視角來理解概念，通過有效地反思回顧、拓展延伸形成以核心概念為主線的知識結構體系、思維體系，以此培養學生整體意識，提升學生的學習遷移能力.

2. 生長性

許多數學概念是在核心概念的基礎上生成的，核心概念具有顯著的生長性、根基性. 在核心概念教學中，教師要打破“講概念+做練習”的教學局面，應重視呈現概念背景，引導學生經歷概念形成過程，揭示不同概念間的內在聯系，以此促進數學概念的自然生長，讓學生學會思考、學會聯想，切實提升學生自主學習的能力.

3. 思維性

數學概念具有高度的抽象性、概括性，為了讓學生全面深刻地理解概念，需要引導學生經歷觀察、分析、抽象、概括等思維活動. 基于此，在實際教學中，教師要認真研究教學內容，將內容問題化，讓學生在問題的引領下積極思考，誘發高階思維活動，提升思維品質.

生長型核心概念教學的教學

實踐

筆者在教學“函數（第1課時）”時，引導學生經歷概念形成、發展、應用等過程，讓學生在自主探究中充分理解概念的內涵與外延、關聯與邏輯. 活動設計如下：

1. 創設情境，引入概念

問題1：生活中有許多“變化和不變”的量，你能列舉一些嗎？

教學說明 問題1是一個開放性問題，為學生營造了一個開放的、自由的學習氛圍. 在問題的引領下，學生積極思考，通過尋找變量和不變量，初步感知研究變量之間關系的必要性，激發學生的學習動機.

問題2：竹筍在其生長期以每天20 cm的速度生長，一根高為15 cm的竹筍，經x天后，其高度是多少呢？

（1）根據題意，完成表1.

[x/天 1 2 3 4 5 … y/cm ][表1]

（2）以上過程，哪個量是變量？哪個量是不變量？

（3）x，y之間存在什么關系？你能用含x的式子來表示y嗎？

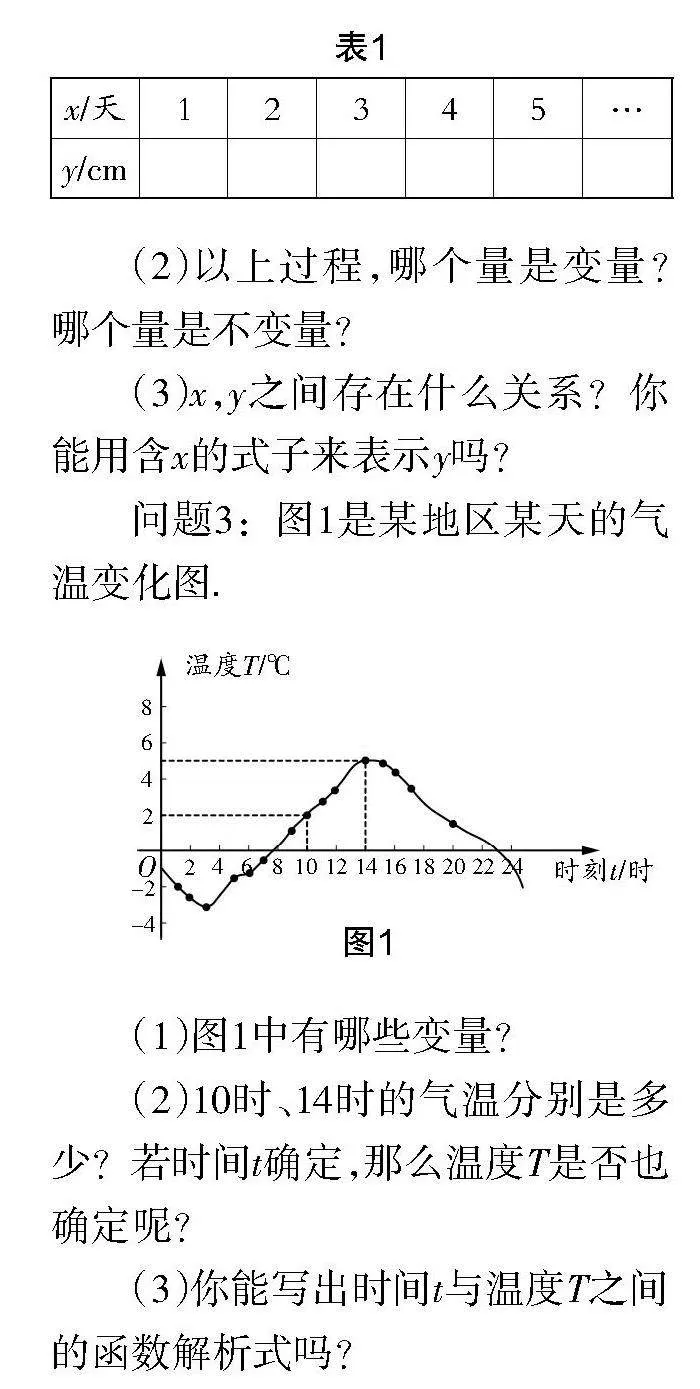
問題3：圖1是某地區某天的氣溫變化圖.

（1）圖1中有哪些變量？

（2）10時、14時的氣溫分別是多少？若時間t確定，那么溫度T是否也確定呢？

（3）你能寫出時間t與溫度T之間的函數解析式嗎？

教學說明 以上問題是圍繞“函數”這一核心概念設計的，旨在借助生活實例讓學生進一步感知“變與不變”的量，繼而為函數概念的生成做鋪墊. 在此環節，教師從學生認知規律出發，精心設計問題，讓學生在思考辨析中初步建立函數概念的表象. 同時，在不同問題中，教師給出了不同的呈現方法，如問題1和問題3中的表格，問題2中的圖象，及相應的函數解析式，讓學生初步感知函數的幾種表示方法.

2. 活動探究，生成概念

問題4：回顧以上3個問題，思考如下問題，

（1）以上3個問題分別有幾個變量？各是什么？

（2）當其中一個變量取確定的值時，另外一個變量有幾個確定的值與之對應？

（3）y與x，T與t之間有何共同點？

在解決以上問題的過程中，教師先讓學生獨立思考，然后進行組內交流，接下來在教師的帶領下進行抽象概括，提煉問題的共同屬性. 在下定義時，教師先是鼓勵學生為函數下定義，然后給出教材中的定義讓學生對比分析，以此幫助學生理解和掌握函數的概念.

教學說明 教師通過創設問題串引導學生回顧以上問題，讓學生通過經歷觀察、思考、分析、比較、概括等活動提煉問題的共同屬性，幫助學生理解概念的本質，提高學生數學抽象、數學建模等素養.

3. 課堂練習，理解概念

問題5：判斷下列說法是否正確？給出你的理由.

（1）在圓的周長公式C=2πr中，C是r的函數.

（2）若y2=x，則y是x的函數.

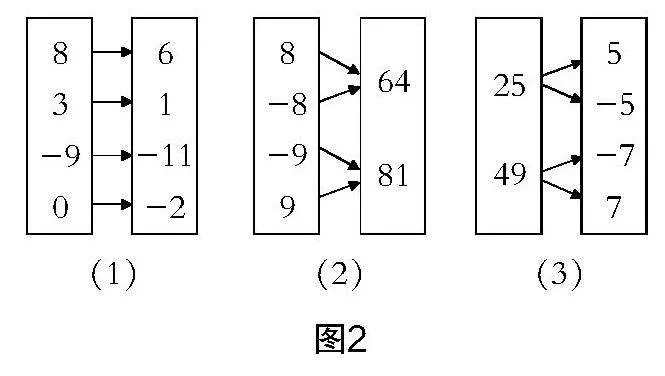
問題6：如圖2所示，若用x表示（1）（2）（3）中左邊的數，y表示（1）（2）（3）中右邊的數，y是否為x的函數？

教學說明 思考辨析是深化概念理解的重要手段，是培養學生思維能力的重要途徑. 在實際教學中，教師可以設計一些正、反例引導學生進行概念辨析，以此讓學生抓住概念的本質，明晰概念的內涵與外延，培養思維的縝密性.

問題7：你能列舉一些生活中存在的函數關系的例子嗎？

教學說明 教師引導學生回歸生活，體會數學與生活的聯系，培養學生數學應用意識. 教學中，教師立足于函數學習的整體視域，通過設計綜合性、開放性、實踐性的問題引發學生深度思考，加深學生對函數本質的理解.

4. 反思總結，形成體系

問題8：結合以下問題談談你的心得體會.

（1）函數的定義是什么？它有哪幾種表示方法？

（2）在研究函數概念時，我們經歷了哪些過程？

（3）通過本課的學習，你有哪些收獲？還想知道什么呢？

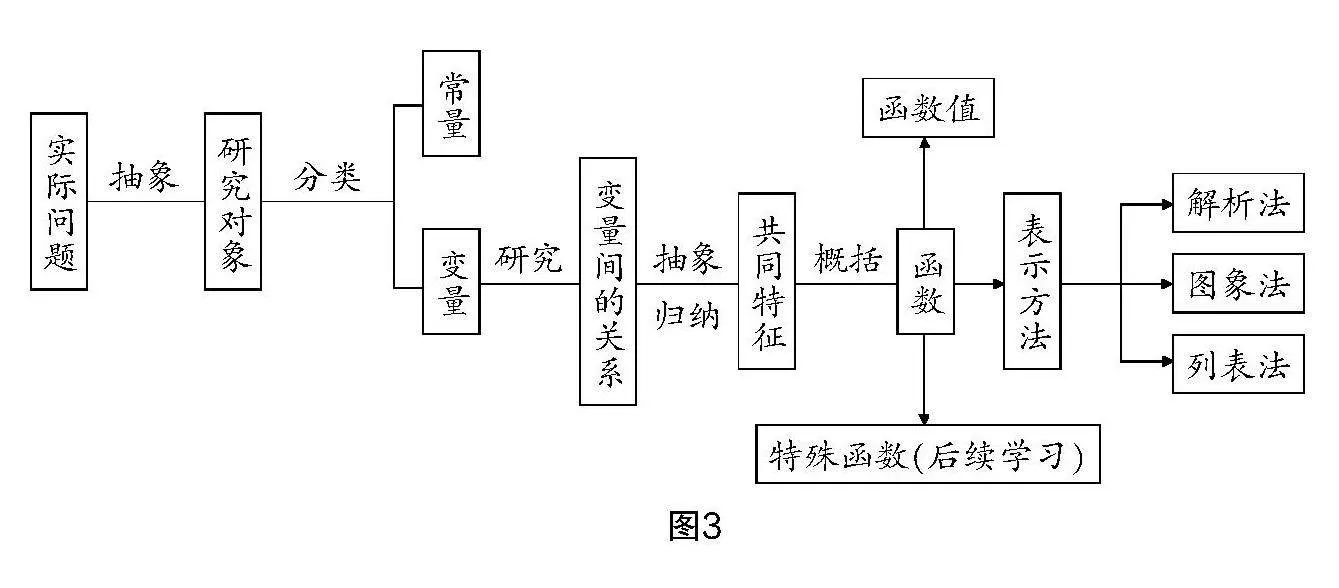
在此環節，通過學生自主反思和生生、師生互動交流，給出如圖3所示的知識框架圖.

教學說明 課堂小結是建構學生知識體系的重要途徑. 教學中，教師要預留充足的時間讓學生回顧與梳理概念的形成過程，讓學生明確概念“從何而來”“要到哪去”，以此幫助學生厘清概念的來龍去脈，讓學生從整體上掌握概念.

總之，在數學概念教學中，教師要改變傳統的講授式概念教學模式，善于站在整體和發展的角度設計有效的問題情境，讓學生養成從基本概念出發思考和解決問題的習慣，實現知識和思維的自然生長、必然生長.