探索知識關(guān)

作者簡介：夏戀（1981—），本科學(xué)歷，中小學(xué)一級教師，從事初中數(shù)學(xué)教學(xué)與研究工作.

[摘 要] “三角形相似成立的條件”與“全等三角形的判定定理”有一定的關(guān)聯(lián)，實踐探究建議從全等出發(fā)，開展定理探索，設(shè)計豐富的實踐活動，引導(dǎo)學(xué)生思考，拓展學(xué)生思維. 文章從知識關(guān)聯(lián)的角度對“探索三角形相似的條件”進行教學(xué)設(shè)計.

[關(guān)鍵詞] 相似三角形;知識關(guān)聯(lián);條件;定理

“探索三角形相似的條件”是蘇教版九年級下冊重要的內(nèi)容，是幾何“空間與圖形”范疇的知識探究. 從整個知識內(nèi)容來看，是對全等三角形知識拓展與發(fā)展，指導(dǎo)學(xué)生掌握三角形相似成立的條件，形成數(shù)學(xué)的思維方式和思想方法是教學(xué)的重點.

基于上述分析，實際教學(xué)中要理清三點：一是從知識的衍生與發(fā)展角度來探索相似成立的條件;二是從條件定理探索的過程思考教學(xué)設(shè)計;三是從應(yīng)用強化角度思考學(xué)生思維能力的提升. 下面結(jié)合教學(xué)核心進行深入探討.

知識關(guān)聯(lián)探討，全等衍生相似

教材將“探索三角形相似的條件”安排在“全等三角形”之后，學(xué)生在學(xué)習(xí)本章節(jié)知識內(nèi)容時已經(jīng)掌握了三角形全等的判定定理，并積累了圖形的性質(zhì)和判定的探究經(jīng)驗. 對于“X5hu0qLvt5wEFBTdKBylxQ==三角形相似的條件”的探索，需要把握兩點：一是知識的關(guān)聯(lián)性，二是知識鏈的完整性. 即注重知識關(guān)聯(lián)，構(gòu)建完整的知識鏈，從全等中衍生相似定理.

從教材內(nèi)容設(shè)計來看，全等三角形與相似三角形之間存在一定的聯(lián)系，可將三角形相似視為全等三角形的“弱化”，即從三角形全等判定定理中衍生三角形相似成立的條件，從而讓新知的生成有理有據(jù)，邏輯關(guān)聯(lián)性強.

教學(xué)推進中需要讓學(xué)生回顧全等知識，思考兩方面問題：

一是三角形全等判定定理有哪些？

二是如何將三角形全等判定定理進行弱化？弱化后是否可以判定三角形相似？

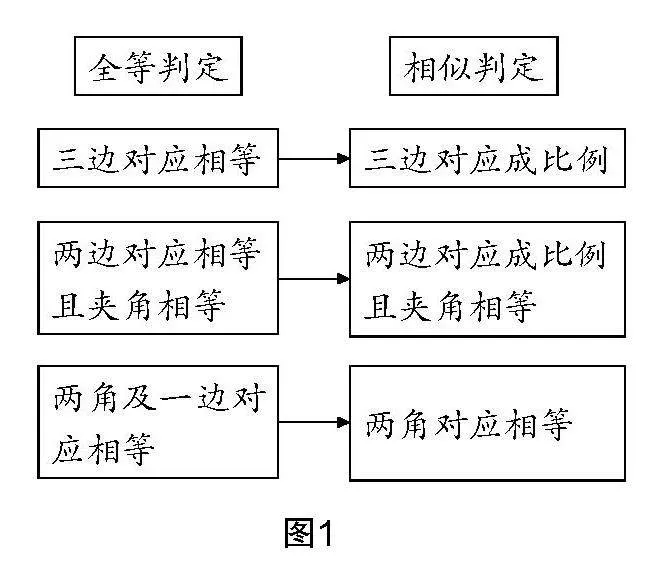
對于三角形全等的四個判定定理：SAS、ASA、AAS、SSS，從兩大視角進行弱化引導(dǎo)：一除去其中的一組對應(yīng)邊相等;二是將其中的對應(yīng)邊相等，弱化為對應(yīng)邊成比例，如圖1所示的弱化對應(yīng)關(guān)系.

基于上述知識關(guān)聯(lián)性、整體性開展的教學(xué)衍生推進，可以構(gòu)建三角形相似成立的條件，實現(xiàn)“全等判定”向“相似判定”的轉(zhuǎn)化.

經(jīng)歷探究過程，定理自然生成

“探索三角形相似的條件”章節(jié)內(nèi)容本質(zhì)上是探究三角形相似的判定定理，屬于定理教學(xué). 下面以三角形相似成立的條件“兩邊對應(yīng)成比例及夾角相等”為例，開展教學(xué)設(shè)計，構(gòu)建教學(xué)活動.

1. 情景引入，啟發(fā)思考

學(xué)生已經(jīng)掌握了三角形全等的判定定理，教學(xué)中弱化定理SAS來引出三角形相似成立的條件.

如圖2所示，在△ABC和△A1B1C1中，已知AB=A1B1，AC=A1C1，∠A=∠A1，兩三角形是什么關(guān)系？請說明所用的判定定理.

在△ABC中點D和E分別是AB和AC的中點，則△ADE與△ABC有怎樣的關(guān)系？請說明理由.

思考：若要使△ADE演變?yōu)椤鰽1B1C1，需要經(jīng)過怎樣的變化？

教學(xué)中從三角形全等的判定定理“SAS”入手，引導(dǎo)學(xué)生關(guān)注圖形“縮放”后形成的相似關(guān)系. 同時“A”型相似圖形的“疊放特點”有利于學(xué)生把握“對應(yīng)邊成比例”這一性質(zhì). 教學(xué)中注意對條件的羅列對應(yīng)，直觀呈現(xiàn)邊的比例關(guān)系，可引導(dǎo)學(xué)生填寫下表.

2. 活動體驗，相似思考

活動一：請同學(xué)們準備一張三角形紙片，思考怎樣剪可以獲得一個與已知三角形紙片相似的三角形紙片，小組討論，共享方案.

活動二：按照如下方案來裁剪三角形.

方案1：在已知的三角形上畫一條邊的平行線，沿著平行線截得三角形，再在紙片上畫出與截得三角形全等的三角形，并剪下來.

方案2：先畫一個與已知三角形中某角相等的角，再分別將該角的兩邊放大或縮小2倍，再將其剪下來.

方案3：如圖3所示，先取三角形三邊的中點，然后按圖連接中點，再將中點三角形剪下來.

設(shè)問：思考三種方案所獲得的三角形與原三角形是否相似？三種方案可以得到怎樣的幾何關(guān)系？

方案1：沿平行線裁剪→兩邊對應(yīng)成比例

方案2：角的兩邊縮放→兩邊對應(yīng)成比例

方案3：連接中點→兩邊對應(yīng)成比例

活動三：在如圖4所示的兩個三角形中，已知∠A=∠A′，對應(yīng)線段關(guān)系如圖，是否可以判定兩個三角形相似？

設(shè)問：請分別計算和的比值，可以得出怎樣的結(jié)論？

3. 辨析說理，定理生成

該環(huán)節(jié)需要引導(dǎo)學(xué)生總結(jié)三角形相似成立的條件，生成定理. 同時引導(dǎo)學(xué)生開展辨析，探究定理的正確性.

辨析思考——以如圖4所示兩個三角形為例

設(shè)問1：若將條件“∠A=∠A1”去掉，兩個三角形是否依然相似？

設(shè)問2：若將條件“∠A=∠A1”替換為“∠B=∠B1”或“∠C=∠C1”，兩個三角形是否還相似？

定理生成——以如圖5所示兩個三角形為例

根據(jù)活動探究，引導(dǎo)學(xué)生陳述兩個三角形相似成立的關(guān)系.

條件：在△ABC和△A′B′C′中，已知∠A=∠A′，=.

結(jié)論：△ABC∽△A′B′C′.

文字語言描述：兩邊對應(yīng)成比例及夾角相等的兩三角形相似.

應(yīng)用遷移體驗，能力強化提升

三角形相似成立的條件在解題中有著廣泛的應(yīng)用，教學(xué)中要開放探索、開放思維，讓學(xué)生在應(yīng)用遷移，思考探索中獲得能力的提升. 問題設(shè)計建議由原型問題進行變式，由易到難，逐步深入，既注重定理強化，又有利于學(xué)生的思維拓展.

總之，“探索三角形相似的條件”的教學(xué)探究要基于內(nèi)容的知識關(guān)聯(lián)和整體性來開展，從三角形全等出發(fā)，探索三角形相似條件;讓學(xué)生經(jīng)歷探究過程，深刻理解定理本質(zhì);合理設(shè)計應(yīng)用問題，以提升學(xué)生的思維能力為重點. 整個教學(xué)環(huán)節(jié)，讓學(xué)生的思想自由發(fā)揮，知識內(nèi)化吸收.