非連續免疫對一類丙型肝炎SICR模型的影響

收稿日期：2023-10-26

基金項目：皖南醫學院科學研究項目（WK202117）

作者簡介：李迅（1991-），男，安徽滁州人，講師，研究方向為微分方程動力系統.E-mail：1123676642@qq.com.

文章編號：2095-6991（2024）04-0006-07

摘要：研究了一類右端不連續的丙肝SICR微分模型，利用微分包含理論和構造Lyapunov函數，證明了模型地方病平衡點和無病平衡點的存在唯一性，通過計算得到了模型的基本再生數R0，分析證明了各平衡點在有限時間內的全局漸近穩定性.文末借助MATLAB數值仿真驗證了理論的準確性.

關鍵詞：右端不連續；微分包含；Filippov解；全局漸近穩定

中圖分類號：O175""" 文獻標志碼：A

Effect of Discontinuous Immunizationon a Class of Hepatitis C SICR Models

LI Xun1， HUANG Jian2， TAO Long3

（1. Nanjing Vocational Health College， Jiangsu Union Technical Institute， Nanjing 210038， China;

2. Public Foundation College， Wannan Medical College， Wuhu 241000， Anhui， China）

Abstract：A class of right end discontinuous SICR differential models for hepatitis C were studied. By using differential inclusion theory and constructing Lyapunov functions， the existence and uniqueness of local and disease-free equilibrium points in the model were proved. The basic reproduction number R0 of the model was calculated， and the global asymptotic stability of each equilibrium point in finite time was analyzed and proved. Finally， the accuracy of the theory was verified by MATLAB numerical simulation.

Key words：right-hand discontinuity; differential inclusion; Filippov solution; global asymptotic stability

丙型肝炎是一種由丙型肝炎病毒（HCV）感染所引起的病毒性肝炎，它是當前誘發肝硬化和肝癌的重要原因.建立數學艙室模型是研究傳染病的主要手段之一.早在1927年，KERMACK和MEKENDRICK開創性地提出了SIR微分模型［1］，為后續的數學傳染病學研究奠定了堅實的基礎. Yuan等［2］提出了一類具有急性和慢性感染階段且人群數量呈指數變化的模型，分析了無病平衡點和有病平衡點的全局穩定性；ELBASHA E H［3］提出一類HCV感染傳播的確定性模型，研究發現抗病毒治療對模型的穩定性具有重要影響；MARTCHEVAM等［4］研究了具有慢性感染階段和可變人群規模的丙型肝炎流行病學模型，研究結果表明：各平衡點的局部平衡是不穩定的，并且可能會發生持續振蕩；STOCKS T等［5］構建了一種PWID人群HCV傳播的多層動態傳播模型，研究表明DAA治療可以有效降低注射吸毒者的丙肝感染風險.CUI J等［6］提出了一類具有急慢性丙型肝炎的流行病學模型，研究發現急性丙型肝炎患者可以自行清除病毒并進入康復類別，而慢性丙型肝炎患者不能自動清除病毒；康玉嬌等［7］在CUI J等［6］的研究基礎上，提出了具有隨機干擾的丙型肝炎模型，研究發現隨機擾動的強度和噪聲的強度具有正相關，且當噪聲足夠大時疾病將會滅絕.

然而以上關于丙肝的研究都是連續依賴于感染者的數量，在某種病毒傳染的初期，感染者的數量較少，人們往往意識不到該病毒的危害性.因此，初期感染的患者往往得不到及時治療甚至沒有治療.而隨著一段時間的傳染，越來越多的易感者被感染疾病，人們意識到問題的嚴重性后就會加大對疾病的治療力度，這勢必會造成病人的數量發生巨減，從而形成一個明顯的治療跳躍.因此，丙肝病毒傳播的過程相對于感染者的數量應是不連續的變化過程.為更加精確地研究丙肝傳染病，有必要將非連續免疫策略引入到丙肝的治療中.

1" 模型的建立

依據文獻［6-7］，建立如下的微分方程動力模型：

dSdt=A－βSI－βSC－aS，

dIdt=βSI+βSC－（a+γ）I－HI，

dCdt=pγI－（a+μ）C，

dRdt=（1－p）γI－aR+HI，（1）

其中：H（I）是非連續治療函數，模型式（1）中各變量和各參數的含義如表1所列，模型中所有的參數都是正的.

記模型的初值為S（0）≥0，I（0）≥0，C（0）≥0，R（0）≥0，模型的種群再生數為

R0=βA（a+μ）+βApγa（a+γ）（a+μ）.

為保證模型不失右端不連續的一般性，提出假設1.

假設1" H（I）=φ（I）·I，φ：R+→R+分段連續且單調不減，即H（I）=φ（I）·I僅有可數個不連續點.

由于模型（1）中關于dS（t）/dt和dR（t）/dt的方程右端是不連續的，故連續微分方程的解理論不適用于模型（1）.

本文考慮采用Filippov解［8］.Filippov解適用于不連續微分方程

dx/dt=f（t，x），（2）

其中，右端函數f（t，x）是關于t和x（t）可測且局部有界的，即f∈L

loc（R×Rn，Rn）.

定義1［9］" 對于集值映射F（t，x）=Kf（t，x）∩δgt;0∩μN=0co （f（t，xδ＼N）），K是加在f上的算子，F（t，x）是由f（t，x）構成的集合.若f（t，x）在一點處連續，則F（t，x）構成單點集合；若f（t，x）在一點處不連續，則F（t，x）構成一凸閉包集合.

由定義1可知，式（2）的解是存在于凸閉包F（t，x）中的函數，即dx/dt∈F（t，x），t∈［0，T）.

由Filippov解的定義可知，右端不連續微分模型的解是絕對連續的向量值函數.即若（S（t），I（t），C（t），R（t））是式（1）的Filippov解，則（S（t），I（t），C（t），R（t））在［0，T）上絕對連續，且滿足

dSdt=A－βSI－βSC－aS，

dIdt=βSI+βSC－（a+γ）I－co［H（I）］，

dCdt=pγI－（a+μ）C，

dRdt=（1－p）γI－aR+co［H（I）］，（3）

其中，co［H（I）］=［H（I－），H（I+）］，H（I－）和H（I+）表示函數H（I）在I處的左極限和右極限.若H（I）在I間斷，則co［H（I）］是存在內點的非空凸閉包；若H（I）在I處連續，則co［H（I）］是一個單點集，且co［H（I）］=H（I）.由可測性選擇定理可知［8］，存在可測函數m（t）∈co［H（I）］，使得對幾乎所有的t∈［0，T）滿足

dSdt=A－βSI－βSC－aS，

dIdt=βSI+βSC－（a+γ）I－m（t），

dCdt=pγI－（a+μ）C，

dRdt=（1－p）γI－aR+m（t）.（4）

2" 平衡點的存在唯一性

下面將證明式（1）地方病平衡點和無病平衡點的存在唯一性.

將模型（1）的方程相加，可得

d（S+I+C+R）dt=

A－aS－aI－（a+μ）C－aR，

即dNdt≤A－aN，其中N=S+I+C+R.

若Ngt;Aa，則limt→+

dNdtlt;0，從而有

N（t）lt;

maxAa，S（0）+I（0）+C（0）+R（0）;

若N≤Aa，則limt→+

dNdt≥0，從而有limt→+

dNdt=Aa，故N（t）≤Aa.

綜上所述，本文的正向不變集為

（S（t），I（t），C（t），R（t））∈R4+：

S+I+C+R≤

maxAa，S（0）+I（0）+C（0）+R（0）.

若假設1成立，則式（3）變為

dSdt=A－βSI－βSC－aS，

dIdt=βSI+βSC－（a+γ）I－co［φ（I）］I，

dCdt=pγI－（a+μ）C，

dRdt=（1－p）γI－aR+co［φ（I）］I.（5）

為得到式（5）的平衡點，需求解下面的微分包含系統：

0=A－βSI－βSC－aS，0∈βSI+βSC－（a+γ）I－co［φ（I）］I，0=pγI－（a+μ）C，0∈（1－p）γI－aR+co［φ（I）］I，（6）

其中co［φ（I）］=［φ（I－），φ（I+）］.

顯然，無病平衡點E0=Aa，0，0，0總是存在的.對于有病平衡點，可先設（S*，I*，C*，R*）是式（5）的有病平衡點，則有

0=A－βS*I*－βS*C*－aS*，0∈βS*I*+βS*C*－

（a+γ）I*－co［φ（I*）］I*，0=pγI*－（a+μ）C*，0∈（1－p）γI*－aR*+co［φ（I*）］I*.（7）

顯然，若（S*，I*，C*，R*）是式（5）的平衡點，則ξ*∈co［φ（I*）］I*，使得ξ*=βS*I*+βS*C*－（a+γ）I*∈co［φ（I*）］I*，其中ξ*是唯一的.即存在η*=ξ*/I*∈co［φ（I*）］，使得式（7）成立.

聯立式（6）中的微分方程，可得

Aβ（a+μ）+Aββ（a+μ+pγ）I+a（a+μ）－

（a+γ）∈co［φ（I）］.（8）

令

g（I）=

Aβ（a+μ）+Aββ（a+μ+pγ）I+a（a+μ）－（a+γ），（9）

很顯然，g（I）是關于I的單調遞減函數.

引理1" 若R0gt;1，則微分包含式（8）存在唯一的正解I∧，且滿足

I∧≤

Aβ+Aβ（a+μ）－a（a+μ）（a+γ）β（a+γ）（a+μ+pγ）.

證明" 首先，證明解的存在性.由于R0gt;1，0lt;p，γlt;1，則

Aβ1－pγ+（R0－1）a（a+μ）（a+γ）β（a+γ）（a+μ+pγ）gt;0，

且g（0）gt;φ（0）gt;0.

由于g（I）是單調遞減函數，故g（I）≤0的充分必要條件是

I≥

Aβ+Aβ（a+μ）－a（a+μ）（a+γ）β（a+γ）（a+μ+pγ），

因而{I：g（I）≥φ（I+），Igt;0}是有界集.令I∧=sup{I：g（I）≥φ（I+），Igt;0}，則有g（I∧）=g（I∧－）≥φ（I∧－），且

0lt;I∧≤

Aβ+Aβ（a+μ）－a（a+μ）（a+γ）β（a+γ）（a+μ+pγ）.

下面證明g（I∧）∈［φ（I∧－），φ（I∧－）］.采用反證法，假定g（I∧）gt;φ（I∧+）=limI→I∧+φ（I），由假設1可知，τgt;0，使得g（I∧+τ）≥φ（I∧+τ）=φ［（I∧+τ）+］，這與I∧的定義矛盾，故g（I∧）∈［φ（I∧－），φ（I∧－）］，即I∧是微分包含式（8）的正解，存在性得證.

接下來證明解的唯一性.假設I1*，I2*是微分包含式（8）的兩個正解，且I1*≠I2*，由式（7）可知，存在η1∈co［φ（I1）］和η2∈co［φ（I2*）］，使得

η1*=

Aβ（a+μ）+Aββ（a+μ+pγ）I*1+a（a+μ）－（a+γ），

η2*=

Aβ（a+μ）+Aββ（a+μ+pγ）I*2+a（a+μ）－（a+γ）.（10）

由假設1可知，φ是非單調遞減的函數，因此函數f=φ（I1）－φ（I2）I1－I2*=η1－η2I1－I2*≥0，將式（10）中的兩式相減可得

η1*－η2*=－β［Aβ（a+μ）+Aβ］

（a+μ+pγ）（I*1－I*2）/

［β（a+μ+pγ）I*1+a（a+μ）］·

［β（a+μ+pγ）I*2+a（a+μ）］.（11）

將式（11）兩邊同時除以I*1－I*2，可得

η1*－η2*I*1－I*2=

－β［Aβ（a+μ）+Aβ］（a+μ+pγ）/

［β（a+μ+pγ）I*1+a（a+μ）］·

［β（a+μ+pγ）I*2+a（a+μ）］.

左邊=f=η1*－η2*I*1－I*2≥0，

右邊=－β［Aβ（a+μ）+Aβ］（a+μ+pγ）/［β（a+μ+pγ）I*1+a（a+μ）］［β（a+μ+pγ）I*2+a（a+μ）］lt;0.

可以發現，左邊≠右邊，這與式（11）等式相等矛盾，故假設不成立，微分包含式（8）有唯一正解，引理得證.

3" 全局漸近穩定

本節將證明模型式（1）各平衡點的全局漸近穩定性，證明之前先給出假設2.

假設2" 若R0gt;1，則φ（I）在I*處有一個跳躍間斷點，其中I*是式（8）所確定的唯一正解，且η=βS*+βS*C*I*－（a+γ）∈（φ－（I），φ+（I））.

根據假設2可定義θ：=min{φ+（I）－η*，η*－φ－（I）}，則必有θgt;0.

定理1" 若假設1和假設2成立，則式（1）滿足初值S（0）≥0，I（0）≥0， C（0）≥0，R（0）≥0的所有解全局穩定于有病平衡點E*=（S*，I*，C*，R*），且在有限時間內趨于穩定，即當

t≥t*=

4a（a+μ）2V1（x（0），y（0），z（0），w（0））4aε（a+μ）2－（a+μ）εβ+εβpγ2θ2

時，有（S（t），I（t），C（t），R（t））=（S*，I*，C*，R*），其中

V1（x（0），y（0），z（0），w（0））=

12［（S（0）－S*）+（I（0）－I*）+

（C（0）－C*）+（R（0）－R*）］2+

ε∫I（0）－I*0φ（I*+ρ）－η*I*+ρdρ.

證明" 令x（t）=S（t）－S*，y（t）=I（t）－I*，z（t）=C（t）－C*，w（t）=R（t）－R*.由式（4）可知，存在可測函數η（t）∈co［φ（I*+y）］，η*∈co［φ（I*）］，則式（5）變為

dxdt=－βx+S*y－βxI*－

βx+S*z－βxC*－ax，dydt=βx（y+I*）+βx（z+C*）－

（η（t）－η*）（y+I*），dzdt=pγy－（a+μ）z，dwdt=（1－p）γy－aw+

η（t）（y+I*）－η*I*.（12）

構造Lyapunov函數

V1（x（t），y（t），z（t），w（t））=

12［x（t）+y（t）+z（t）+w（t）］2+

ε∫y0φ（I*+ρ）－η*I*+ρdρ，

其中，ε是一個確定的正常數，后面將給出其取值范圍.顯然V1（x（t），y（t），z（t），w（t））是關于（x（t），y（t），z（t），w（t））的正則函數.當（x（t），y（t），z（t），w（t））≠0時，V1（x（t），y（t），z（t），w（t））gt;0，當且僅當V1（0，0，0，0）=0；當x（t）→+

或y（t）→+

或z（t）→+

時或w（t）→+

時，V1（x（t），y（t），z（t），w（t））→+

.

對V1（x（t），y（t），z（t），w（t））求關于t的導數，可得

dV1dt=（x+y+z+w）（x′+y′+z′+w′）+

εη（t）－η*y+I*y′=（x+y+z+w）·

［－ax－ay－（a+μ）z－aw］+

εη（t）－η*y+I*［βx（y+I*）+βx（z+C*）－

（η（t）－η*）（y+I*）］≤

－ax2+εβ（η（t）－η*）x+

εβpγa+μ（η（t）－η*）x－ε（η（t）－η*）2=

－ax－（a+μ）εβ+εβpγ2a（a+μ）（η（t）－η*）2－

4aε（a+μ）2－（a+μ）εβ+εβpγ24a（a+μ）2＼5

（η（t）－η*）2，

令4aε（a+μ）2－（a+μ）εβ+εβpγ24a（a+μ）2gt;0，則0lt;εlt;4a（a+μ）2（a+μ）β+βpγ2，從而有dV1dt≤0.

由假設2可知，當（x（t），y（t），z（t），w（t））≠0時，有（η（t）－η*）2gt;θ2，故對于任意的t∈{t：（x（t），y（t），z（t），w（t）））≠（0，0，0，0）}，有

dV1dt≤

－4aε（a+μ）2－（a+μ）εβ+εβpγ24a（a+μ）2θ2.（13）

對式（13）兩邊從0到t進行積分，有

0≤V1（x（t），y（t），z（t），w（t））≤

V1（x（0），y（0），z（0），w（0））－

4aε（a+μ）2－（a+μ）εβ+εβpγ24a（a+μ）2θ2t，

這意味著V1（x，y，z，w）在t=t*時到達0，這里

t*=

4a（a+μ）2V1（x（0），y（0），z（0），w（0））4aε（a+μ）2－（a+μ）εβ+εβpγ2θ2.

由文獻［10］可知，當

tgt;t*時，對任意的t都有（x（t），y（t），z（t），w（t））=0，故有（S－S*，I－I*，C－C*，R－R*）=（0，0，0，0），即當tgt;t*時，有（S（t），I（t），C（t），R（t））=（S*，I*，C*，R*），定理1得證.

接下來證明式（5）無病平衡點的全局漸近穩定性.由于假設1不符合在零點右端不連續的假定，故提出假設3.

假設3" H（I）：（0，+

）→（0，+

）是單調遞增且至多存在有限個間斷點的函數，I=0是函數H（I）的間斷點，且H（0）=0.

定理2" 若模型式（5）滿足假設3，當R0lt;1時，它的解都將在有限時間內全局漸近穩定于無病平衡點E0=（S0，0，0，0），即當tgt;t*時，（S（t），I（t），C（t），R（t））=Aa，0，0，0，且V2（x（0），I（0），C（0），C（0））=12（S（0）－S*）2+aI（0）.

證明" 令x（t）=S（t）－S0，則式（5）變為

dxdt=－βx+S0I－" βx+S0C－ax，

dIdt=βx+S0I+βx+S0C－

（a+γ）I－H（I），

dCdt=pγI－（a+μ）C，

dRdt=（1－p）γI－aR+H（I），（14）

構造Lyapunov函數

V2（x（t），I（t），C（t），R（t））=

12［x（t）+I（t）+C（t）+R（t）］2+aI（t）.

顯然，V2（x（t），I（t），C（t），R（t））是正則函數.當（x（t），I（t），C（t），R（t））≠0時，V2（x（t），I（t），C（t），R（t））gt;0，當且僅當V2（0，0，0，0）=0.

對V2（x（t），I（t），C（t），R（t））求導數，可得

dV2（x（t），I（t），C（t），R（t））dt=

（x+I+C+R）（x′+I′+C′+R′）+aI′≤

（x+I+C+R）（－ax－aI－aC－aR）+

aβx+AaI+βx+AaC－（a+γ）I－H（I）≤

－axI－axC+aβxI+aβxC+βAI+

βAC－a（a+γ）I－aH（I）=

－a（1－β）xI－a（1－β）xC+

βA（a+μ）+βApγ－a（a+γ）（a+μ）a+μI－

aH（I）≤－a（1－β）xI－a（1－β）xC－

（1－R0）aa+γI－aH（I）.

由于R0lt;1，0≤β≤1，則

dV2（x（t），I（t），C（t），R（t））dt≤－aη（t）.

由假設3可知η（t）≥H（0+），故有

dV2（x（t），I1（t），I2（t））dt≤－aH（0+），

對兩邊做從0到t的積分，可得

0≤V2（x（t），I（t），C（t），R（t））≤V2（x（0），I（0），C（0），R（0））－aH（0+）t.

當

tgt;t*=V2（x（0），I（0），C（0），R（0））aH（0+）

時，由文獻［11］可知，有V2（x（t），I（t），C（t），R（t））=0.即當tgt;t*時，

（x（t），I（t），C（t），R（t））=（0，0，0，0），故有（S－S0，I（t），C（t），R（t））=（0，0，0，0），即（S（t），I（t），C（t），R（t））=（S0，0，0，0），定理2得證.

4" MATLAB數值仿真

本節將運用MATLAB軟件仿真模擬驗證結論的正確性．

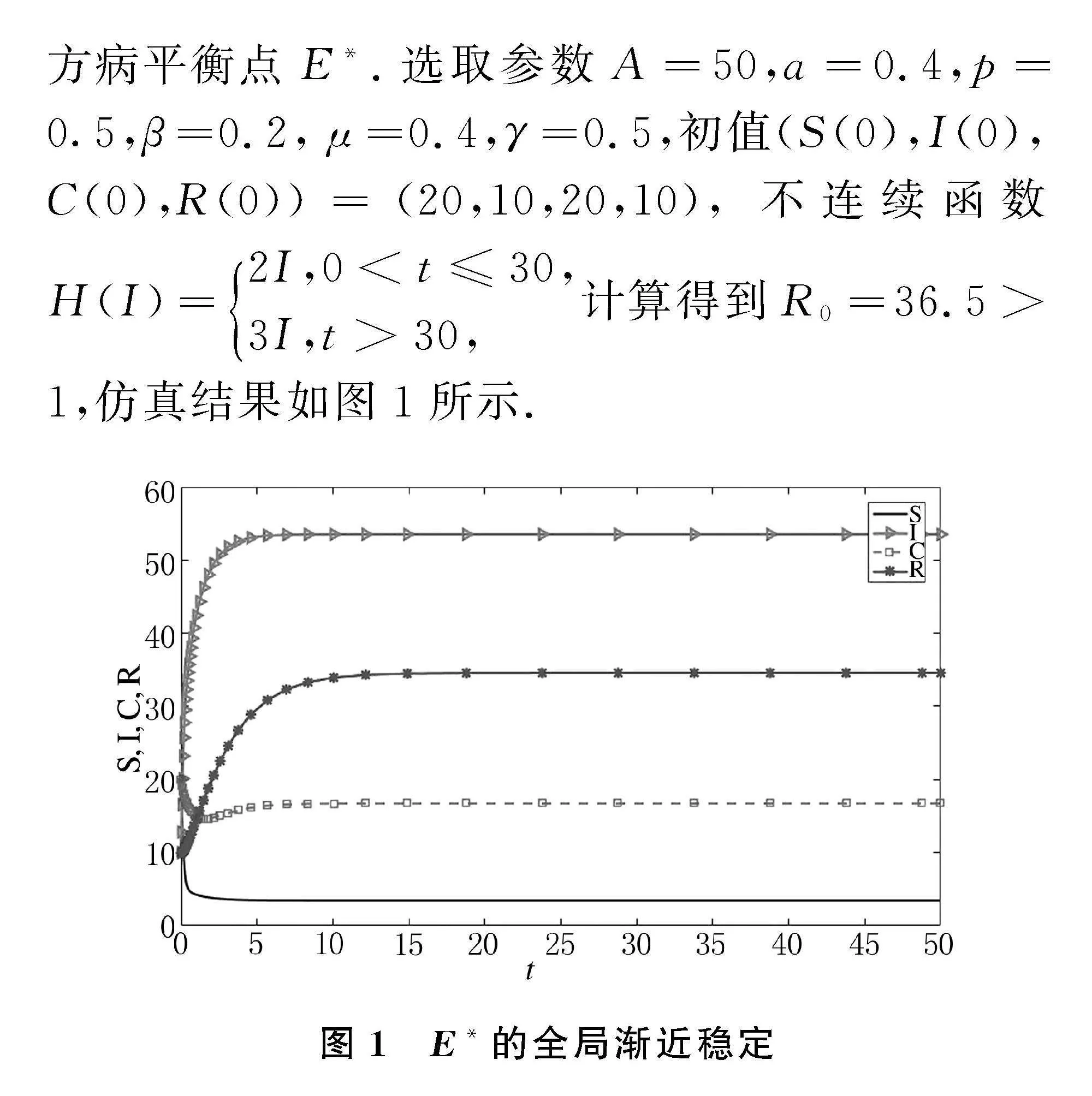
4.1" 地方病平衡點的數值仿真

根據假設1和定理1可知，當R0gt;1時，模型式（5）的解都將在有限時間內全局漸近穩定于地方病平衡點E*.選取參數A=50，a=0.4，p=0.5，β=0.2， μ=0.4，γ=0.5，初值（S（0），I（0），C（0），R（0））=（20，10，20，10），不連續函數H（I）=2I，0lt;t≤30，3I，tgt;30，計算得到R0=36.5gt;1，仿真結果如圖1所示.

4.2" 無病平衡點的數值仿真

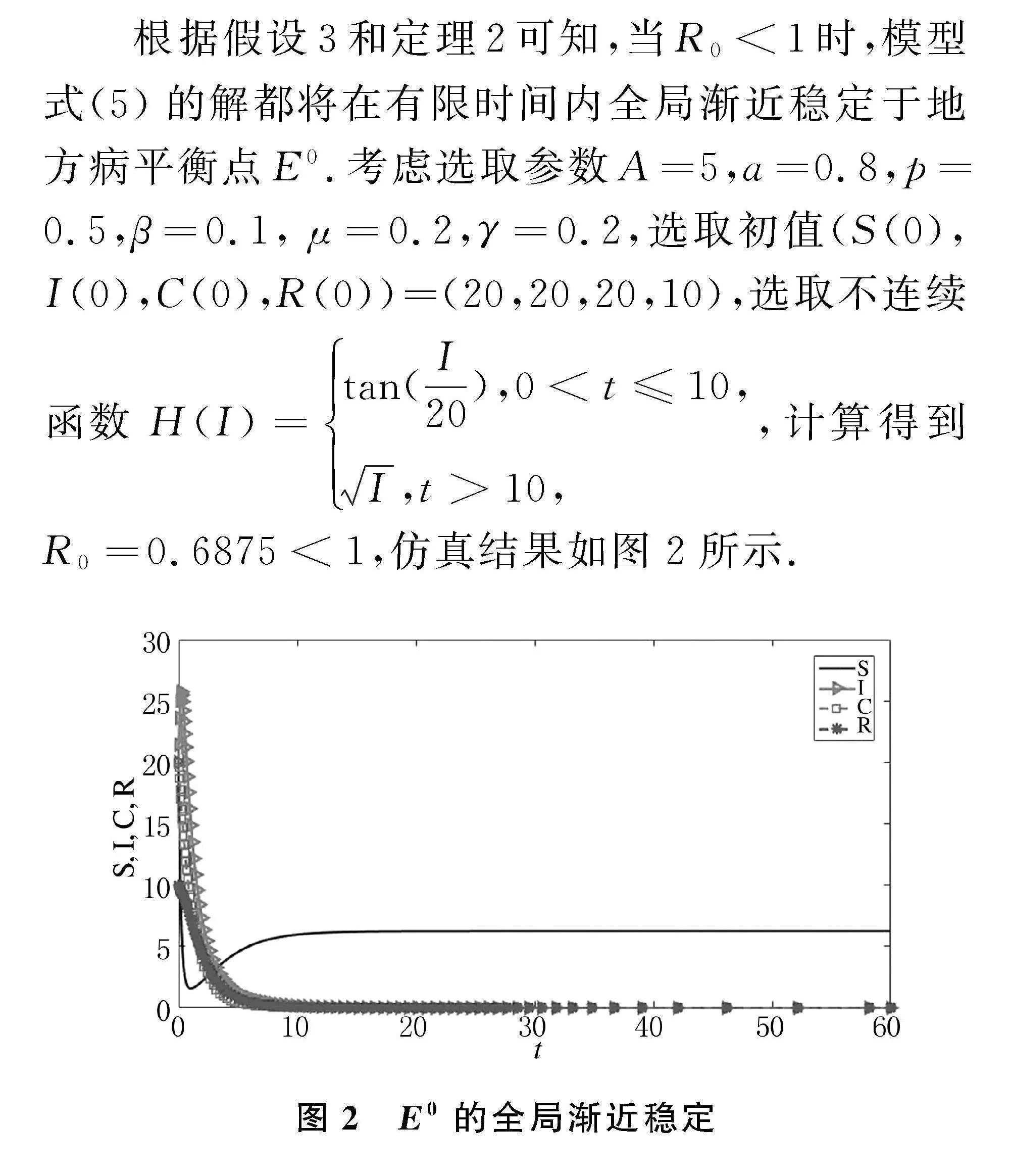
根據假設3和定理2可知，當R0lt;1時，模型式（5）的解都將在有限時間內全局漸近穩定于地方病平衡點E0.考慮選取參數A=5，a=0.8，p=0.5，β=0.1， μ=0.2，γ=0.2，選取初值（S（0），I（0），C（0），R（0））=（20，20，20，10），選取不連續函數H（I）=tan（I20），0lt;t≤10，I，tgt;10，，計算得到R0=0.6875lt;1，仿真結果如圖2所示.

圖2" E0的全局漸近穩定

5" 結語

為了分析非連續治療策略對丙型肝炎傳染病模型的影響，通過引入右端不連續治療函數H（I），研究了模型各平衡點的存在唯一性.通過研究得到如下結論.

（1）當 R0 gt;1時，在有限時間內，模型的所有Filippov解全局漸近穩定于有病平衡點E*；當 R0lt;1時，在有限時間內，模型的所有Filippov解全局漸近穩定于無病平衡點E0.

（2）“有限時間內被治愈”具有重要的現實意義，因為患者總是想知道自己的疾病能否被治愈、何時被治愈.利用MATLAB軟件對此不連續模型進行了數值仿真，驗證了定理1和定理2的正確性.

（3）基于上述研究，還可將非連續免疫策略應用到更多領域中，如神經網絡系統和捕食系統［11-12］，以期獲得更符合現實規律的結論.

參考文獻：

［1］ KERMACK W O，MEKENDRICK A G.Coutributions to the mathematical theory of epidemics［J］.Bu-lleition of Mathematical Biology，1991，53（1-3）：33-51.

［2］ YUAN Junli ，YANG Zuodong.Global dynamics of an SEI model with acute and chronic stages［J］.Journal of Computational and Applied Mathematics，2007，213（2）：465-476.

［3］ ELBASHA E H.Model for hepatitis C virus transmissions［J］.Mathematical Biosciences and Engineering：MBE，2013，10（4）：1045-1065.

［4］ MARTCHEVA M，CASTILLO-CHAVEZ C.Diseases with Chronic Stage in a Population with Varying Size［J］.Mathematical Biosciences，2003，182（1）：1-25.

［5］ STOCKS T，MARTIN L J，KUHLMANN-BERENZON S，et al.Dynamic Modeling of Hepatitis C Transmission Among People Who Inject Drug［J］.Epidemics，2020，30：100378.

［6］ CUI Jingan，ZHAO Shifang，GUO Songbai，et al.Global Dynamics of an Epidemiological Model with Acute and Chronic HCV Infections［J］.J Applied Mathematics Letters，2020，103：106203.

［7］ 康玉嬌，張太雷，馬怡婷.一類隨機SICR丙肝模型的動力學分析［J］.哈爾濱理工大學學報，2023，28（3）：129-139.

［8］ FILIPPOV A F.Dfferential Equations with Disconti-nuous Right-hand Sides［M］.Boston：Kluwer Academic，1988：10-35.

［9］ 黃立宏，郭振遠，王佳伏.右端不連續微分方程理論與應用［M］.北京：科學出版社，2011：28-29.

［10］ FORTI M，GRAZZINI M，NISTRI P，et al.Genera-lized Lyapunov approach for convergence of neural networks with discontinuous or non-Lipschitz activations［J］.Physica D：nonlinear phenomena，2006，214（1）：88-89.

［11］ 王小娥，藺小林，李建全.具有Holling Ⅳ型功能反應捕食系統的狀態反饋控制［J］.應用數學和力學，2020，41（12）：1369-1380.

［12］ 李葛.幾類不連續神經網絡模型的動力學研究［D］.長沙：湖南大學，2019.

［責任編輯：趙慧霞］