固定配平飛行器多約束再入制導(dǎo)方法研究

王楷,郭金雷,郝蓮英,施振興,劉益吉

(上海機電工程研究所,上海 201109)

具有機動能力的再入飛行器具有提升突防效能、提高命中精度的優(yōu)勢,因而成為飛行器再入技術(shù)的重要研究方向。在各種再入機動飛行器設(shè)計中,最簡單經(jīng)濟的方案之一就是采用一維滾動控制的固定配平飛行器[1]。

固定配平飛行器是利用飛行器外形不對稱或質(zhì)心偏移產(chǎn)生不可控的配平攻角,通過滾轉(zhuǎn)單通道控制改變配平升力的方向,實現(xiàn)再入機動飛行。但這種單通道控制特性給制導(dǎo)帶來了很大困難,缺少合適的制導(dǎo)方法是制約這種不對稱再入體多約束條件下落點精確控制的主要瓶頸。

目前國內(nèi)外針對這類飛行器含約束條件下實現(xiàn)精確打擊的制導(dǎo)律研究文獻較少,這種外形的應(yīng)用也多集中在航天器返回等終端約束要求不高的情況。傳統(tǒng)的彈道-升力式返回航天器再入過程以縱向多約束制導(dǎo)為主,側(cè)向采用速度傾側(cè)角正負切換的方式控制橫程偏差,但這種方法在顧及飛行器姿控穩(wěn)定性和可實現(xiàn)性條件下難以獲得較高的落點精度。美國MK500機動彈頭則采用程序飛行方式,以犧牲精度換取機動能力[2]。Gracey等[3]針對固定配平攻角飛行器的特點提出了滾轉(zhuǎn)制導(dǎo)律,有效實現(xiàn)了固定配平飛行器的精確制導(dǎo)并解決了多余升力消耗問題,但是難以在制導(dǎo)律中處理各項約束條件。文獻[4]在滾轉(zhuǎn)制導(dǎo)律基礎(chǔ)上通過引入具有一定運動規(guī)律的虛擬目標作為引導(dǎo),實現(xiàn)了在不改變制導(dǎo)律形式情況下對落角的有效控制,但這與滿足再入過程的多約束條件還有一定距離。

針對固定配平攻角飛行器多約束條件下再入精確制導(dǎo)問題,本文提出將軌跡優(yōu)化和滾轉(zhuǎn)制導(dǎo)律相結(jié)合,利用高斯偽譜法收斂速度快、精度高的特點實現(xiàn)標準軌跡的快速優(yōu)化,滿足多約束條件,然后采用滾轉(zhuǎn)制導(dǎo)律+虛擬目標的方式實現(xiàn)對標準軌跡的跟蹤,解決精確制導(dǎo)問題。

1 固定配平飛行器再入制導(dǎo)問題

1.1 固定配平飛行器模型

固定配平飛行器具有以下特點:

1) 俯仰、偏航通道通過配置適當靜穩(wěn)定度實現(xiàn)自穩(wěn)定,不施加控制;

2) 穩(wěn)定飛行條件下,飛行器攻角為固定配平攻角α=α*,側(cè)滑角為β=0;

3) 僅通過滾動控制改變γV實現(xiàn)機動飛行即可實現(xiàn)對彈道的控制。

假設(shè)地球模型為均勻球體,固定配平飛行器再入制導(dǎo)模型為

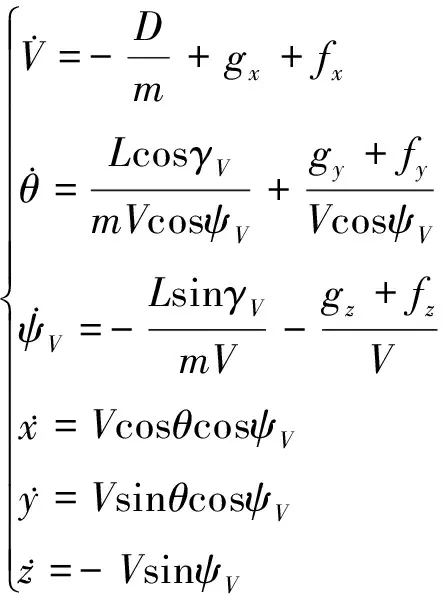
(1)

式中,各狀態(tài)變量為[V,θ,ψV,x,y,z]T,各元素依次為飛行器速度、彈道傾角、彈道偏角和飛行器在再入系下的位置坐標;控制量為速度傾側(cè)角γV;D,L分別為彈體所受阻力和升力;(gx,gy,gz)T為引力加速度在彈道系下的投影;(fx,fy,fz)T為地球自轉(zhuǎn)引起的慣性加速度和哥式加速度在彈道系的投影。

1.2 再入制導(dǎo)約束條件

作為對地打擊武器的再入機動飛行器,再入制導(dǎo)問題需要考慮以下幾類約束:

1) 過程約束

從結(jié)構(gòu)安全和熱防護角度出發(fā),再入飛行器通常對動壓和過載的上限提出要求,即

(2)

2) 終端約束

為了保證精度,應(yīng)滿足嚴格的落點位置約束。以再入系中的坐標來描述,期望落點的位置可以根據(jù)目標射程推算。

x(tf)=xf,y(tf)=yf,z(tf)=zf

(3)

為了保證攻擊效果、提高突防能力,通常對終端落角和落速提出要求,終端時刻自由,即

V(tf)≥Vf,θ(tf)≤θf

(4)

式中,落角約束應(yīng)以當?shù)貜椀纼A角為準,為了簡便可以根據(jù)目標射程,針對地球曲率造成的傾角偏差值對落角約束指標進行修正。

3) 初始狀態(tài)約束

初始狀態(tài)固定為指定的再入條件

(5)

1.3 固定配平飛行器再入制導(dǎo)面臨的困難

1) 制導(dǎo)指令的實現(xiàn)

經(jīng)典的制導(dǎo)設(shè)計方法通常將三維制導(dǎo)問題分解為縱、側(cè)向2個平面的二維制導(dǎo)問題,分別設(shè)計制導(dǎo)律,進而會得到縱向和側(cè)向2個方向的過載指令。采用STT或BTT控制的飛行器可以分別按直角坐標和極坐標方式實現(xiàn)2個方向的過載指令。然而固定配平攻角飛行器由于升力大小不可控,只能控制升力方向,無法同時滿足上述2個維度制導(dǎo)指令。

2) 過剩升力的消耗

由于飛行器配平攻角不可控,無法實現(xiàn)零升力彈道,在升力過剩時需要有適當?shù)闹茖?dǎo)律來消耗多余的升力[5]。

3) 再入過程的多約束條件

再入過程需要滿足的終端約束、過程約束和控制約束條件是再入制導(dǎo)的典型問題,進一步增大了固定配平飛行器制導(dǎo)律的設(shè)計難度。

因此實現(xiàn)固定配平飛行器多約束條件下精確打擊,就要求制導(dǎo)律同時解決上述3個問題。本文認為,多約束問題可以通過軌跡優(yōu)化有效解決,而前2個問題則在軌跡跟蹤時予以解決。

2 基于高斯偽譜法的標準軌跡優(yōu)化

2.1 再入制導(dǎo)問題

取狀態(tài)變量x(t)=[V,θ,ψV,x,y,z]T,控制變量為u(t)=γV。為了提高突防效果,選取落速最大為性能指標

minJ=-V(tf)

(6)

為了使高斯偽譜法解算方便,可對動力學方程進行無量綱化處理。

固定配平飛行器再入軌跡優(yōu)化[6]可歸納為:滿足微分方程約束(1)和1.2節(jié)所述各終端約束、過程約束的Mayer型最優(yōu)控制問題

(7)

2.2 高斯偽譜法求解

高斯偽譜法是將狀態(tài)變量和控制變量在一系列LG點上離散,并以離散點為節(jié)點構(gòu)造Lagrange插值多項式來逼近狀態(tài)變量和控制變量,從而將連續(xù)的最優(yōu)控制問題轉(zhuǎn)化為具有一系列代數(shù)約束的有限維非線性規(guī)劃(NLP)問題。

按照高斯偽譜法求解的常規(guī)步驟[7],最優(yōu)控制問題(7)可離散為在N個LG點τk(k=1,2,…,N)和1個初始點τ0=-1共N+1個離散節(jié)點上,尋求狀態(tài)變量X(τk)、控制量U(τk)和終端時刻tf,使性能指標(8)最小,并滿足動力學方程約束(9)、邊界條件約束(10)和過程約束(11)的非線性優(yōu)化問題。

式中,D∈RN×(N+1)為微分近似矩陣。

本文采用成熟的序列二次規(guī)劃(SQP)方法求解標準軌跡優(yōu)化的NLP問題。

3 標準軌跡的跟蹤

3.1 固定配平飛行器的標準軌跡跟蹤問題

對于固定配平飛行器,經(jīng)典的標準軌跡跟蹤方法以和約束指標直接相關(guān)的縱向制導(dǎo)為主,例如采用如(12)式所示的跟蹤制導(dǎo)律

(12)

這種制導(dǎo)律傾側(cè)角指令是開關(guān)式的不連續(xù)信號,在接近目標時傾側(cè)角正負切換的頻率變高。這種快速的滾動與頻繁的方向切換不僅對飛行穩(wěn)定性不利,也對控制系統(tǒng)提出了過高的要求。在滾轉(zhuǎn)速度受限情況下會造成較大的落點偏差。因此這種方法僅適用于精度要求不高的場合。

為了實現(xiàn)對標準軌跡的有效跟蹤,并獲得較高的制導(dǎo)精度,本文采用針對固定配平飛行器設(shè)計的滾轉(zhuǎn)制導(dǎo)方法,通過設(shè)置虛擬目標實現(xiàn)對標準軌跡的跟蹤。

3.2 滾轉(zhuǎn)制導(dǎo)律

如圖1所示,O為飛行器質(zhì)點,T為目標質(zhì)點,Oxyz為彈道坐標系。定義飛行器速度矢量V和彈目視線構(gòu)成的平面為誤差平面,同時定義速度矢量與彈目視線的夾角為誤差角η(0°≤η≤180°)。為方便描述,定義誤差系Ox′y′z′,其中Ox′與速度矢量重合,Oy′軸在誤差平面內(nèi),指向彈目視線一側(cè)。記誤差平面和彈道坐標系Oxy平面的夾角為ξ,順著Ox方向看,Oy順時針轉(zhuǎn)動到Oy′時為正;飛行器配平升力L與彈道坐標系Oxy平面的夾角即為傾側(cè)角γV。根據(jù)定義,ξ和γV均在Oyz平面內(nèi)。

圖1 滾轉(zhuǎn)制導(dǎo)示意圖

進而可得到三自由度相對運動方程組如(13)式所示,其中前2個方程描述了誤差平面內(nèi)的相對運動關(guān)系,第三個方程描述了誤差平面的旋轉(zhuǎn)。

(13)

式中

(14)

滾轉(zhuǎn)制導(dǎo)律的思想是使誤差平面內(nèi)的彈目距離r和誤差角η收斂到0,而誤差平面的旋轉(zhuǎn)角度ξ不影響r和η的收斂,因此可以不施加控制。

在誤差平面內(nèi)建立滾轉(zhuǎn)制導(dǎo)律的制導(dǎo)方程為

(15)

式中,K為制導(dǎo)系數(shù),取值應(yīng)滿足K>1。有關(guān)證明可參考文獻[5]。進而可得到滾轉(zhuǎn)制導(dǎo)律的制導(dǎo)指令表達式為

(16)

式中

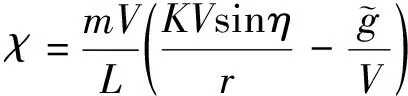
(17)

3.3 基于虛擬目標的標準軌跡跟蹤

令虛擬目標沿優(yōu)化得到的標準軌跡運動,飛行器按照滾轉(zhuǎn)制導(dǎo)律對其進行跟蹤。虛擬目標取為標準軌跡上飛行器前方縱程相距ΔS處,即任意時刻可根據(jù)飛行器當前縱程S和ΔS在標準軌跡上插值得到其位置坐標。

當虛擬目標與真實目標(標準軌跡落點)重合后不再繼續(xù)運動,之后再入飛行末段退化為簡單的打擊固定目標的滾轉(zhuǎn)制導(dǎo)。

3.4 制導(dǎo)方法穩(wěn)定性

在不考慮目標運動時,可以證明[5],在等式(15)的約束下(對應(yīng)飛行器升力L對誤差角η的控制能力不小于自由運動對誤差角的影響),當K>1時,可有效控制誤差角η趨于0。

當飛行器接近虛擬目標時,彈目視線距離r較小,(15)式不成立,此時飛行器因機動能力不足導(dǎo)致制導(dǎo)律不收斂,并最終產(chǎn)生制導(dǎo)方法誤差。為了減小該影響,保證較高制導(dǎo)精度,應(yīng)在虛擬目標設(shè)置時,避免ΔS過小觸發(fā)上述條件;另一方面在末段虛擬目標與標準軌跡落點重合后,可通過設(shè)計合理的制導(dǎo)系數(shù)與飛行速度,減小進入不收斂的時間。

考慮虛擬目標速度情況下,制導(dǎo)律穩(wěn)定性分析可參考文獻[4],經(jīng)證明有上文類似結(jié)論,即在飛行器機動能力足夠抵消誤差影響時,誤差角可收斂至0,并實現(xiàn)飛行器與虛擬目標呈尾追狀態(tài)。

本文采用滾轉(zhuǎn)制導(dǎo)律跟蹤虛擬目標時,假設(shè)虛擬目標每一時刻都是靜止的,因此制導(dǎo)律中未顯式包含虛擬目標的速度項,這使得在標準軌跡上插值確定虛擬目標位置時,避免了獲取其速度的額外處理,該方法在不影響制導(dǎo)律穩(wěn)定性基礎(chǔ)上,有利于工程實現(xiàn)[8]。當虛擬目標與標準軌跡落點重合后問題完全轉(zhuǎn)化為滾轉(zhuǎn)制導(dǎo)律穩(wěn)定性問題。

4 仿真驗證與調(diào)參分析

以下通過三自由度仿真對本文提出的制導(dǎo)方法進行仿真驗證。

假設(shè)飛行器姿態(tài)保持配平攻角α=5°,配平側(cè)滑角β=0°。初始條件和約束指標見表1。

表1 初始條件和約束指標

4.1 標準軌跡優(yōu)化

取節(jié)點個數(shù)N=25進行高斯偽譜法軌跡優(yōu)化,優(yōu)化結(jié)果如圖2所示。

圖2 標準軌跡彈道曲線

1) 優(yōu)化所得的標準軌跡主要指標為落速1 154 m/s,落角-72.7°,軸向最大過載30.6g,法向最大過載33.4g,最大動壓2.15 MPa,均能滿足約束條件。

2) 飛行器通過平緩變化的傾側(cè)角指令實現(xiàn)了縱向平面彈道在約30 km高度處的拉起減速及低空段的高拋彈道,滿足了過程約束和終端約束要求,傾側(cè)角指令變化速度不超過15°/s。

3) 傾側(cè)角曲線顯示優(yōu)化后的標準軌跡仍是通過正反2個方向的滾轉(zhuǎn)實現(xiàn)多余升力的消耗,但優(yōu)化后的滾轉(zhuǎn)指令遠比傳統(tǒng)方法更容易跟蹤實現(xiàn)。

4.2 軌跡跟蹤

采用“虛擬目標+滾轉(zhuǎn)制導(dǎo)律”的方法對以上優(yōu)化所得的標準軌跡進行跟蹤。取滾轉(zhuǎn)制導(dǎo)律制導(dǎo)系數(shù)為K=1.4,虛擬目標位于飛行器前方縱程相距ΔS=49 km的標準軌跡上。部分仿真結(jié)果如圖3所示。

圖3 三維彈道曲線

根據(jù)仿真結(jié)果可得以下結(jié)論:

1) 使用滾轉(zhuǎn)制導(dǎo)律可以比較有效地實現(xiàn)對標稱軌跡的跟蹤,在滾轉(zhuǎn)限速條件下,實際彈道主要指標為落速1 236.5 m/s,落角-59.6°,軸向最大過載31.5g,法向最大過載33.3g,最大動壓2.18 MPa,各指標參數(shù)與標稱軌跡接近。實際彈道落點偏差為29 m,這對于機動能力有限的固定配平攻角再入飛行器來說是合理的。

2) 使用滾轉(zhuǎn)制導(dǎo)律雖然可以使各指標參數(shù)與標準軌跡接近,但仍存在一定偏差,難以實現(xiàn)實際彈道對標稱軌跡的精確跟蹤。這是因為固定配平攻角飛行器升力機動控制能力有限,采用的滾轉(zhuǎn)制導(dǎo)律具有如下特點:在機動能力不足時產(chǎn)生跟蹤誤差,在機動能力過剩時以螺旋接近方式消耗多余升力。再入過程中滾轉(zhuǎn)制導(dǎo)律的上述制導(dǎo)效果將體現(xiàn)在實際彈道中,進而必然和標準軌跡產(chǎn)生差異。尤其是在飛行末段,虛擬目標和實際目標重合后,跟蹤標準軌跡問題已退化為打擊固定目標的滾轉(zhuǎn)制導(dǎo),彈道明顯體現(xiàn)出滾轉(zhuǎn)制導(dǎo)律的特點,與標準軌跡無關(guān)。此時飛行器已經(jīng)過動壓和過載峰值點,因此這種退化一般不影響過程約束的滿足情況,但彈道傾角會由于螺旋接近方式出現(xiàn)小幅振蕩(見圖4)。

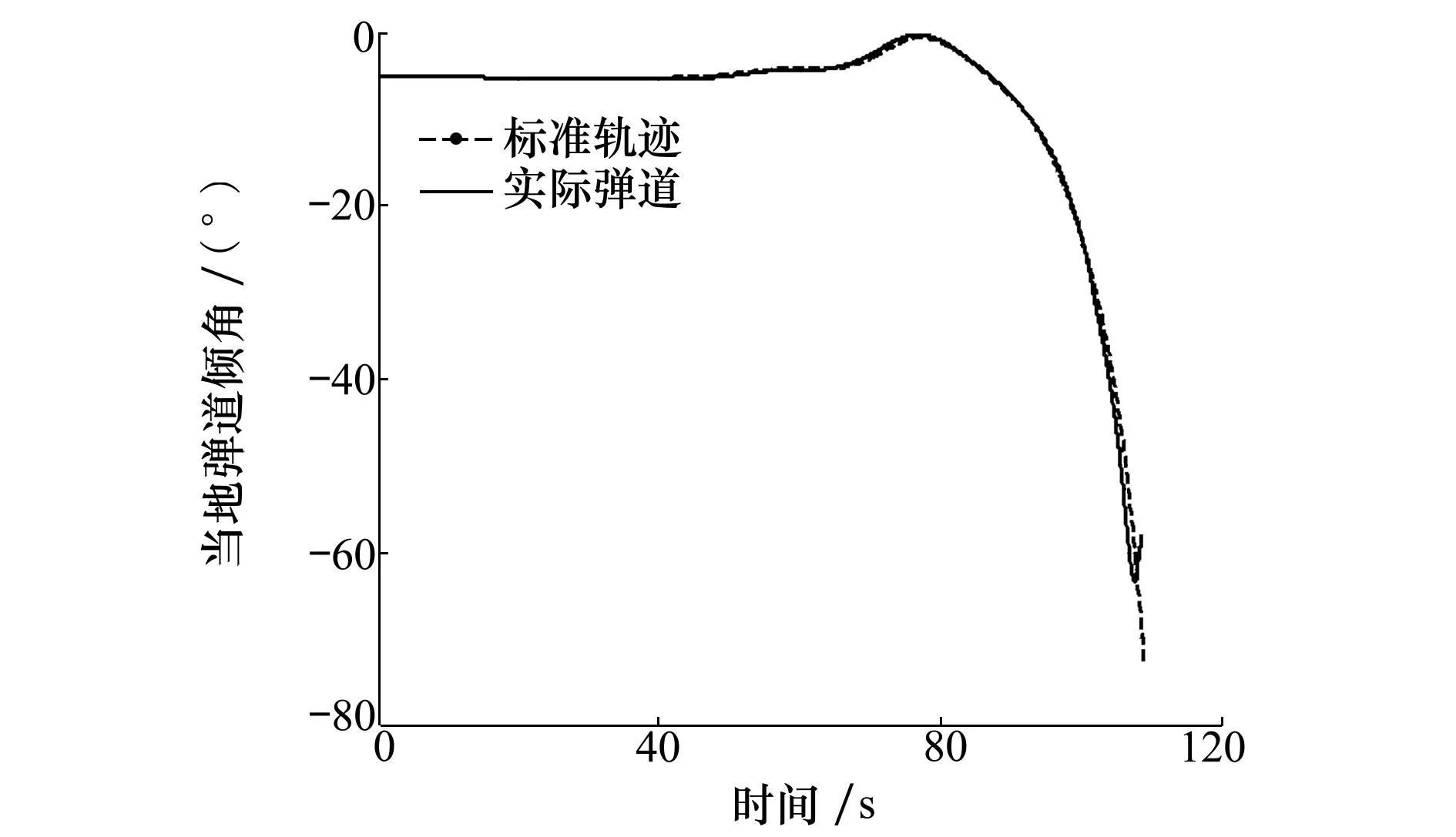
圖4 當?shù)貜椀纼A角變化曲線

3) 考慮到滾轉(zhuǎn)制導(dǎo)律對標準軌跡的上述跟蹤誤差,以及參數(shù)拉偏條件下的制導(dǎo)偏差,軌跡優(yōu)化時設(shè)置的約束指標應(yīng)該比給定的約束條件更加嚴格,以預(yù)留足夠的裕度。

在軌跡跟蹤時,虛擬目標位置ΔS、制導(dǎo)系數(shù)K和滾轉(zhuǎn)角速度限幅大小均會對落點精度和約束指標產(chǎn)生顯著影響,大量仿真顯示,制導(dǎo)參數(shù)影響有以下規(guī)律:

1) 在正常跟蹤情況下,過載、動壓約束基本與標準軌跡一致,制導(dǎo)參數(shù)變化影響較小(1%以內(nèi))。

2) 虛擬目標位置ΔS的設(shè)置是實現(xiàn)軌跡跟蹤最關(guān)鍵的參數(shù),對落點偏差和落速(落角)都有顯著影響。不同ΔS條件下仿真結(jié)果統(tǒng)計如表2。

表2 ΔS取值對主要指標的影響

可見,在一定范圍內(nèi),ΔS取值越大,落點精度提高,同時落速減小,反之亦然。超出該范圍后,繼續(xù)增大ΔS并不能繼續(xù)提高精度,而落速仍會快速降低,這是由滾轉(zhuǎn)速度受限情況下滾轉(zhuǎn)制導(dǎo)律自身的方法誤差造成的。同樣,ΔS取值過小并不能繼續(xù)提高落速,而精度則會快速下降,這是由過程約束和標準軌跡限制造成的。因此應(yīng)綜合考慮精度和落速的要求選擇適當?shù)摩值。

3) 制導(dǎo)系數(shù)K的影響與滾轉(zhuǎn)制導(dǎo)律影響規(guī)律一致。即隨著K增大,最大滾轉(zhuǎn)角速度增大,落點精度在一定范圍內(nèi)有所提高,受限于滾轉(zhuǎn)制導(dǎo)律方法誤差,繼續(xù)增大K落點精度不會繼續(xù)提高。因此K的取值可根據(jù)滾轉(zhuǎn)制導(dǎo)律本身的要求進行設(shè)計。

4) ΔS的最優(yōu)取值與制導(dǎo)系數(shù)K大小有關(guān)。仿真顯示,在精度、落速、落角指標接近情況下,若K=1.4,ΔS=49 km,而K=1.6時ΔS應(yīng)取35 km,K=1.8時ΔS應(yīng)取19 km。因此制導(dǎo)律設(shè)計時應(yīng)首先針對滾轉(zhuǎn)制導(dǎo)律確定適當?shù)腒值,在此基礎(chǔ)上優(yōu)化調(diào)整ΔS。

5) 與滾轉(zhuǎn)制導(dǎo)律影響規(guī)律一致,滾轉(zhuǎn)角速度增大有助于提高落點精度。但滾轉(zhuǎn)速度過快會使姿態(tài)運動的穩(wěn)定性變差,并且滾轉(zhuǎn)控制系統(tǒng)難以實現(xiàn),因此應(yīng)根據(jù)飛行器姿控能力對滾轉(zhuǎn)速度進行適當限幅。

6) ΔS的取值也可以根據(jù)需要設(shè)計成時變參數(shù),在不同的飛行階段,或者不同飛行狀態(tài)下,利用ΔS的變化,兼顧落速、精度等不同指標的要求。

5 結(jié) 論

本文采用“高斯偽譜法軌跡優(yōu)化+滾轉(zhuǎn)制導(dǎo)律跟蹤標準軌跡”的方法,解決了固定配平攻角飛行器多約束條件下再入精確制導(dǎo)問題。仿真結(jié)果顯示,該方法可有效解決再入過程的各項終端約束、過程約束問題,并獲得滿意的落點精度。同時該方法除了依靠軌跡優(yōu)化滿足約束條件外,采用滾轉(zhuǎn)制導(dǎo)律跟蹤標準軌跡時,虛擬目標的設(shè)置也會對最終的精度和落速產(chǎn)生影響。根據(jù)仿真分析總結(jié),該制導(dǎo)方法在設(shè)計和參數(shù)設(shè)置時,有以下規(guī)律:

1) 因固定配平攻角飛行器升力機動控制能力有限,實際跟蹤彈道會與軌跡優(yōu)化所得標準軌跡存在跟蹤偏差,采用高斯偽譜法進行軌跡優(yōu)化時,設(shè)置的約束指標應(yīng)該比給定的約束條件更加嚴格,以預(yù)留足夠的裕度。

2) 制導(dǎo)律設(shè)計時應(yīng)首先確定適當?shù)闹茖?dǎo)系數(shù)K值,K的影響與滾轉(zhuǎn)制導(dǎo)律影響規(guī)律一致,可根據(jù)滾轉(zhuǎn)制導(dǎo)律本身的要求進行設(shè)計。在滿足滾轉(zhuǎn)制導(dǎo)律穩(wěn)定性前提下,K增大,落點精度在一定范圍內(nèi)有所提高,但繼續(xù)增大K落點精度不會繼續(xù)提高,同時考慮到工程實際中最大滾轉(zhuǎn)角速度的限制,K的取值不宜過大,必要時根據(jù)飛行器姿控能力對滾轉(zhuǎn)速度進行適當限幅。

3)K值確定后,可在此基礎(chǔ)上確定虛擬目標位置ΔS。在一定范圍內(nèi),ΔS取值越大,落點精度提高,同時落速減小,反之亦然。超出該范圍后,繼續(xù)增大ΔS并不能繼續(xù)提高精度,而落速仍會快速降低。同樣,ΔS取值過小并不能繼續(xù)提高落速,而精度則會快速下降。因此需根據(jù)實際情況,綜合考慮精度和落速的要求,通過仿真等手段對ΔS取值進行參數(shù)優(yōu)選。更精細的設(shè)計中,可將ΔS取為時變參數(shù),在不同的飛行階段利用ΔS的變化,更好地兼顧各項約束指標。

4) ΔS的最優(yōu)取值與制導(dǎo)系數(shù)K大小有關(guān),若K有調(diào)整,虛擬目標位置ΔS也應(yīng)相應(yīng)優(yōu)化。K越大,在實現(xiàn)相近的指標時,ΔS應(yīng)設(shè)置得越小。