基于認知不確定可靠性的產品功能優化算法研究

鐘維宇,戴儼炯,蔡敢為,柳林燕

(1. 空軍航空維修技術學院 航空電子設備維修學院,湖南 長沙 410129;2. 廣西大學 機械工程學院,廣西 南寧 530004; 3. 南京理工大學 機械工程學院,江蘇 南京 210094)

0 引言

隨著智能制造飛速發展,產品功能趨向多樣化、復雜化和專業化,產品設計過程以系統可靠性、功能性、確定性為設計基準,大力倡導模塊化、系列化、通用化設計理念,以實現產品多功能及專業性全覆蓋。

可靠性作為產品的重要設計屬性之一,在不確定因素下產品可靠性的高低直接決定了產品能否高品質、無故障地工作運行。影響可靠度評估的不確定因素太多,且涉及的問題較多。方永鋒等[1]將可靠性指標轉化為隨機可靠性指標,得到區間參數串聯、并聯的表決系統可靠度計算方法;歐陽惠卿等[2]將串-并聯系統和優化后并-串聯系統的可靠性進行了推導計算。但以上研究對于不確定可靠度理論與分析方法尚存在不足。

產品設計的方案階段,以產品的功能分析為主,進行產品的總功能、子功能分解,功能優化設計過程中存在多個復雜的、相互沖突的優化目標,故傳統的方法在處理時受到很大的約束。因此,建立不確定可靠性產品功能算法模型,對多個優化目標進行分析求解,尋找最佳的目標方案組合,以實現產品方案設計與功能優化設計并行[3]。

1 認知不確定可靠性方法

產品功能優化分析中不確定可靠性主要分為兩類:隨機不確定性、認知不確定性。認知不確定可靠性即通過概率理論反映產品功能優化過程中認知不確定性的主觀因素及客觀因素。

認知不確定方法將產品總功能、子功能、細分功能等分別轉化為認知集合,形成由可信度和似真度組成的認知不確定概率區間。

認知集合定義為影響產品功能的一切不確定性因素的集合,其子元素兩兩互斥通常用Λ表示。

(1)

式中:u1為認知集合Λ的子元素;n是子元素個數,i=1,2,3,…,n。

設計者對不同功能子集進行分析闡述,確保認知不確定性的真實、可靠、牢固。此過程等同于對認知集合進行積分運算,又稱為基本可信度分配,需滿足以下公式:

(2)

式中:m為基本可信度分配函數;x為認知集合所對應的2Λ的任意子集;m(x)為事件x的可信概率。

基本可信度分配反映了命題x為真實的信任程度。目前,針對基本可信度分配函數,常用的構型有貝葉斯型構型、概率型構型及輔助型構型,任何子集在區間范圍內,可信度概率位于[0,1]區間內。

產品不同功能需求來源及實現方式不同,處理不確定信息的多元化程度,合成認知集合中命題的總信任程度至關重要。目前,常見的合成法則有Dempster、Yager、Inagaki等[4-6]。

認知集合Λ中子集G,對于可信度和似真度可以采用區間集合[B(G),P(G)],兩個指標集合組成Λ的信任程度:

(3)

(4)

式中:B(G)是子集命題G中的命題x完全包含于認知集合G基本可信度之和;P(G)是子集命題G中的命題x與子集命題G交集不為空的基本可信度之和。當P(G)與B(G)所形成的區間敞口越大,說明信息的不確定性加大。真實的可靠度一定介于可信度和似真度之間,B(G)和P(G)滿足以下公式:

(5)

Bel(G1∪G2)≥B(G1)+Bel(G2)-B(G1∩G2)

(6)

P(G1∩G2)≤P(G1)+P(G2)-P(G1∩G2)

(7)

2 認知不確定可靠性算法模型

基于認知不確定可靠性產品功能設計優化是一個繁復和龐大的計算過程,在給定設計輸入不確定性的情況下,設計者無法判別功能需求不確定性等因素,根據不同需求認知不確定性基本可信度,考慮實際產品設計過程中時效性,低值不確定性功能的問題可以選擇近似替代初始模型并通過樣本策略構建高效的模型[3,5]。

綜合考慮多種不確定因素條件下選定目標可靠度,尋找最優不確定設計變量的表達式:

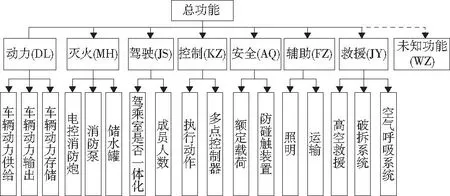
F={g:g(Xi)

(8)

(存在:vart、x;最小邊界minf(t,x);

s.t. Prob(Gj(t,x)≥0)≥1-Φ(-βj);

tb≤t≤tp;j=1,2,…,p

式中:g0為目標產品可靠性失效值;Xi為相互獨立的不確定性變量識別集合;F為失效域;x是不確定功能變量,即認知集合所對應的2Λ的任意子集。

認知不確定可靠性模型采取區間集合[B,P],集合中左邊界(下限)為B和右邊界(上限)為P,β是約束目標參考可靠度;t=[t1,t2…,tn]T是產品設計變量向量;tb表示其下限值,tp表示其上限值。

概率約束是計算極限狀態函數在隨機變量輸入積分區域gi(x)<0的概率。考慮到極限狀態函數與聯合概率密度函數求解的復雜性,工程計算一般采用空間轉換再積分的方法進行簡化。首先,設均值和方差分別為ux和σx,通過標準化轉換后的現有空間成為u空間,則有

(9)

相應的u空間可靠性積分公式展示為

(10)

(11)

相應得出u空間中獨立變量的聯合概率密度函數可表示為

(12)

采用功能度量法進行逆可靠性分析,可靠度指標法的目標函數及約束相互對偶,功能度量法的數學模型可表示為:

(13)

為了找到可靠性指標β的逆可靠性分析來找到功能度量法,通過分析其靈敏性,通過獲取設計靈敏度,定義如下:

(14)

從而可得u*對設計變量的靈敏度用微分式子來表達如下:

(15)

(16)

(17)

在X空間的功能評估變換矩陣T和Hessian矩陣H,如式(18)所示;X空間中功能的靈敏度以矩陣形式表示,如式(19)所示。可以獲得在u空間中功能靈敏度相對于設計變量的靈敏度,從而優化獲取最優解組合。

(18)

(19)

上述認知不確定可靠性數學模型作為真實系統行為決策的近似表達,不確定性功能數據來源于現實需求、理論假設和經驗相關性。該方法將不確定性功能變量轉換成概率變量,構建等效的概率可靠性設計優化模型,每個不確定變量在其平均值附近分配概率分布,然后通過數學模型將此不確定性傳播到輸出,通過計算機迭代求解,使用數值技術來產生數學模型的近似解。上述模型僅限于求解連續方程的離散近似解,執行最優解篩選Λ={uS},S為優選功能[7]。

3 認知不確定可靠性算法計算流程

根據認知可靠性模型,構建認知可靠性計算程序,其計算步驟程序既嚴謹又可調節,需根據實際產品的復雜程度和真實需求,對相關計算步驟進行適當裁剪[8-9],如圖1所示。

圖1 認知不確定可靠性計算流程

步驟一:總體功能分析

產品總體功能分析主要包含總體系統定義及產品功能原理初步分析,轉變為認知集合。總體系統定義為產品功能信息梳理、歸納及定義,包括產品的主要功能、產品的構成等。根據總體功能分析的結果,梳理出各功能對應的確定性要求。每個功能對應的需求可能是一對一或一對多。

步驟二:子功能概率化及可信度分配

產品子功能概率化包括功能原理細化及關鍵特征,轉變為識別集合。功能原理細化采用圖表分析法,繪制產品功能框圖,明確完成子功能的各組件可能的方案。針對識別集合中不確定因素進行變量化處理,采用Dempster合成法則,形成可信度分配。若可信度分配中可信度與似真度敞口過大,代表信息不確定性過強,返回總體功能分析層,進行優化完善;若可信度分配中可信度與似真度敞口合適,代表信息不確定性合適。

步驟三:最優不確定設計變量

選擇初始樣本點,將認知集合信任度中[B,P]、可靠性失效值分別作為可靠性失效方程邊界及約束。可靠性失效值明確主要功能喪失時各相關的功能性能參數邊界值,在分析時應當注明使用約束參數的取值。可靠性失效值一般通過查詢產品相關領域產品設計或驗收規范,結合產品設計功能需求,在適當加嚴后得到產品失效值分析方法;接下來,輸入認知不確定可靠性計算最優解模型,進行函數空間變化,變換后形成聯合概率模型,便于提前進行相應功能調整。

步驟四:迭代計算獲取優選功能組合

采用功能度量法,獲取極限狀態函數,分析設計靈敏度,計算出可靠性指標,滿足收斂標準,即可獲得優選功能組合,以確保此過程中方法的準確性。

4 算例

本文以舉高消防車為例進行產品功能優化分析。舉高消防車功能復雜、作業模式及作戰效率要求高。應解決產品在設計初期遇到的不確定因素干擾,從而提升產品可靠性。

4.1 舉高消防車總體功能分解

總功能分解是多種技術系統的綜合分析,設計者初期應直觀地分辨產品具體功能、區分不同功能種類,從而形成完整的技術方案。舉高消防車功能需求主要包含性能、環境、可靠性等方面,舉高消防車總功能具體按動力、滅火、駕駛、控制、安全、輔助、救援及未知功能(可擴展)來描述[10],如圖2所示。

圖2 舉高消防車總功能分解圖

將舉高消防車總功能定義為認知集合Λ,動力功能(DL)包含車輛動力供給u1、車輛動力輸出u2,依次類推,則認知集合Λ={u1,u2,u3,…,u18}。

4.2 舉高消防車子功能概率化及可信度分配

舉高消防車認知集合中子元素u1,u2,u3,…,u18(即不同功能)來源于N個不同的信息源頭,包含同類產品技術水平、技術數據、技術方案、試驗數據等,這些信息中有確定性、不確定性、真實、虛假等類別。以舉高消防車滅火功能為例進行子功能分解如表1所示。

表1 舉高消防車滅火功能(MH)子功能

滅火功能(MH)模塊子集分別為u4、u5、u6,u4中包含以下幾種子功能:水B1、泡沫滅火劑B2、干粉滅火劑B3、鹵代烷滅火劑B4及其他未知信息B5,故其識別集合為{B1,B2,B3,B4,B5}。同理,可以得出u5、u6的識別集合。

識別集合中子元素之間矛盾較小,采用Dempster合成法則,根據式(2)得到識別集合基本可信度分配m(u4)、m(u5)、m(u6)。

根據式(3)、式(4),選用標準正態分布進行隨機變量化,形成認知集合基本可信度分配m(MH)。在已知可信度分配的基礎上,對于采用可信度和似真度組成的區間[B(G),P(G)]產生可信度和似真度如表2所示,信息不確定性敞口區間為[0.136 4,0.591 9]。

表2 舉高消防車功能可信度及似真度區間

根據不同功能模塊的可信度和似真度、設計經驗數據及企業參數來源,最終確定Λ的信任程度為0.263 2。

4.3 舉高消防車認知可靠性優選功能組合

以認知不確定可靠性計算流程(圖1)為基礎,確定最優不確定變量設計(即初始樣本點)方案,可靠性失效值分別作為可靠性失效方程邊界及約束,結合聯合概率函數及極限狀態函數,進行函數空間變化,采用功能度量法,分析設計靈敏度,計算出可靠性指標,滿足收斂標準,即可獲得優選功能組合。

計算過程中采用SQL Server數據庫系統,滿足大量計算數據處理、數據庫管理模塊及企業級數據開發要求,系統開發主要采用Visual Studio(VS)。優選功能組合計算流程代碼如圖3所示。

圖3 優選功能組合計算流程代碼

根據客戶對產品功能、性能的要求可以進行舉高消防車優選功能重組。比如根據客戶對駕駛室的乘員人數要求,改變駕駛室的人員參數,且系統各功能之間具有關聯性、系列化、互換性[8-10]。功能度量法收斂策略如圖4所示,獲得城市主戰消防車最優功能模塊劃分結果如表3所示。舉高消防車優選功能分為A-D 4種組合,不同組合對應相應的靈敏度數值,A組合的靈敏度值最小,故優先選擇A組合進行優化設計。

表3 舉高消防車優選功能組合

圖4 功能度量法收斂策略

5 結語

本文構建基于認知不確定可靠性產品功能優化算法流程,根據總體功能分析、子功能概率化、可信度分配、最優不確定設計變量及迭代計算獲取優選功能組合等步驟,計算出可靠性指標,針對目標多組解決方案,求解出指定概率滿足一組約束的最優解。舉高消防車的研發是一個具體而復雜的過程,其中包含確定性功能需求、不確定性功能需求及未知功能需求。基于認知不確定可靠性優化模型,以舉高消防車為例,進行需求分析及功能分解,建立認知集合,代入認知不確定可靠性算法流程,獲取滿足設計需求最優功能解,對增強企業新產品開發能力及核心競爭力、提高產品設計可靠性、避免大量冗余工作具有重要的意義。