Stewart并聯機構運動Jacobian矩陣表達形式的多樣性

尤晶晶,葉鵬達,徐帥,王澍聲,黃寧寧,李成剛

(1. 南京林業大學 機械電子工程學院,江蘇 南京 210037; 2. 常州大學 機械與軌道交通學院,江蘇 常州 213164;3. 南京航空航天大學 機電學院,江蘇 南京 210016)

0 引言

與串聯機構相比,并聯機構具有更緊湊的結構、更高的剛度、更快的響應、更小的累積誤差等優勢[1],在多維傳感器[2-3]等領域應用前景廣闊。在所有的6自由度并聯機構中,目前應用最廣的是Stewart并聯機構[4-5]。它主要由1個動平臺、1個靜平臺以及連接2個平臺的6條SPS(S為球面副,P為移動副)支鏈構成。研究發現,Stewart并聯機構的很多性能指標,如奇異性、靈活性、各向同性、剛度、可操作度等,都與機構的Jacobian矩陣有關[6]。Jacobian矩陣包括運動Jacobian矩陣和力Jacobian矩陣,它們之間滿足對偶性的關系。因此,推導并分析Stewart并聯機構的運動Jacobian矩陣有著重要的理論意義和實際價值。

從檢索到的文獻資料來看,并聯機構運動Jacobian矩陣的表達形式五花八門[6-11],且各形式在機構學上的解釋以及它們之間的數學關聯尚不明確。這影響了機構性能的機理分析和機構拓撲的優化。為解決上述問題,本文從動平臺速度的物理定義和數學表達出發,挖掘了Stewart并聯機構運動Jacobian矩陣的內涵,推導并梳理了3類Jacobian矩陣的解析表達式,繼而剖析了不同形式Jacobian矩陣之間以及它們行列式之間的映射關系。最后,通過數值算例驗證了本文結果的正確性,并基于推導出的運動Jacobian矩陣繪制了Stewart并聯機構的位置奇異曲面和姿態奇異曲面。

1 轉動速度采用不同的表達方式

Stewart并聯機構的機構簡圖如圖1所示。

圖1 Stewart并聯機構的機構簡圖

分別在靜平臺和動平臺上固連笛卡兒坐標系O-xyz和P-x′y′z′。初始狀態下,兩坐標系的3個坐標軸分別平行。動平臺的自由度為6,包括3維平動和3維轉動。其中,3維轉動的速度可以用歐拉角及其導數來描述,也可以用角速度矢量來描述。

1.1 歐拉角方式

1)基于歐拉角的旋轉矩陣

首先,P-x′y′z′繞z′軸轉動進動角Ψ(逆時針方向為正),得到第1次轉動之后的坐標系P-x″y″z′。兩坐標系之間的旋轉矩陣為

(1a)

接著,P-x″y″z′繞x″軸轉動章動角θ,得到第2次轉動之后的坐標系P-x″y?z″。它與第1次轉動之后坐標系之間的旋轉矩陣為

(1b)

最后,P-x″y?z″繞z″軸轉動自轉角φ,得到第3次轉動之后的坐標系P-x?y″″z″。它與第2次轉動之后坐標系之間的旋轉矩陣為

(1c)

執行關于3個繞體軸的子旋轉矩陣式(1a)、式(1b)、式(1c)的右乘運算,得到合成的旋轉矩陣:

(2)

2)Jacobian矩陣的推導

Stewart并聯機構的幾何約束方程[12]為

(3)

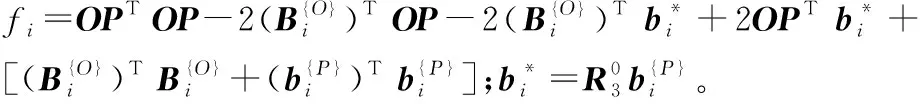
式(3)的等號兩邊同時對時間求一階導數,整理后可得線性方程組

(4)

當li≠0,(i=1～6)時,矩陣Jl是可逆的。此時,式(4)可改寫為

(5)

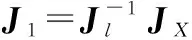
1.2 角速度矢量方式

運用環路方程法[4],列出支鏈速率的解析式:

(6)

式中:si表示第i條支鏈的方向矢量[4];ω表示動平臺的角速度矢量。

將式(6)整理成矩陣形式:

(7)

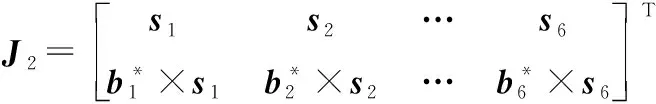
1.3 第1、2類形式Jacobian矩陣之間的映射

根據角速度加法公式,可得坐標系P-x?y″″z″相對于P-x′y′z′的轉動速度:

(8)

(9)

綜合式(5)、式(7)和式(9),整理可得第1、2類形式Jacobian矩陣之間的映射關系:

J1=J2T1,2

(10)

也就是說,通過映射矩陣T1,2可以將第1、2類形式的Jacobian矩陣關聯起來。

2 平動速度選取不同的基點

理論上,動平臺三維平動的速度基點可以任意選擇。常用的基點主要有2個:1)動平臺的質心(一般也是動坐標系的原點)[4];2)動平臺上與靜坐標系原點重合的點[13]。第1節在建立平動速度時就是選取的前者,故本節僅討論后者的情況。

2.1 Jacobian矩陣的推導

將動平臺上與靜坐標系原點重合的點標記為點O′。同樣,運用環路方程法,列出支鏈速率的解析表達式:

(11)

式中vO′表示O′點的線速度矢量。

將式(11)整理成矩陣形式:

(12)

2.2 第2、3類形式Jacobian矩陣之間的映射

根據速度基點法,可建立O′和P兩點速度之間的關系式:

(13)

(14)

綜合式(7)、式(12)和式(14),整理可得第2、3類形式Jacobian矩陣之間的映射關系:

J3=J2T3,2

(15)

可見,通過映射矩陣T3,2可以將第2、3類形式的Jacobian矩陣關聯起來。

2.3 第1、3類形式Jacobian矩陣之間的映射

綜合式(10)、式(15),整理可得第1、3類形式Jacobian矩陣之間的映射關系:

J3=J1T3,1

(16)

式中T3,1=T1,2-1T3,2將第1、3類形式的Jacobian矩陣關聯起來。注意:本文不考慮歐拉角奇異點的情況,即默認矩陣T1,2是可逆的。

3 映射矩陣的算例驗證

本節對Stewart并聯機構在一般位姿下3類形式的運動Jacobian矩陣及其映射矩陣進行算例驗證。并聯機構尺寸參數的選取如表1所示。

表1 Stewart并聯機構的尺寸參數 單位:mm

不失一般性地,隨機選擇動平臺在其工作空間內的一個位姿:OP=(82,158,68)Tmm,Ψ=1.2 rad,θ=2.5 rad,φ=1.7 rad。根據式(3),此時,6條支鏈的長度(單位:mm)依次為298.541、141.327、181.274、322.265、388.781、277.387。對應的3類形式的Jacobian矩陣以及3個映射運算分別如式(17a)—式(17f)所示。結果顯示:1)3個Jacobian矩陣的前3列元素完全相同;2)3個Jacobian矩陣之間的關聯和本文的推導結論完全一致。

(17a)

(17b)

(17c)

(17d)

(17e)

(17f)

4 奇異位形

當并聯機構的Jacobian矩陣的行列式等于0時,動平臺所處的位形稱為“奇異位形”[14]。本節研究3類形式Jacobian矩陣的行列式之間的關聯。

運用矩陣行列式的乘法定理和分塊矩陣的行列式性質,分別處理式(10)、式(15),整理可得:

|J1|=|J2||T1,2|=|J2||A|=-sθ×|J2|

(18)

|J3|=|J2||T3,2|=|J2|

(19)

由于本文不考慮歐拉角奇異點的情況,即sθ不等于0,故由式(18)、式(19)可知:3類形式Jacobian矩陣的行列式等于0的情況是完全等效的。因此,可以通過求解任意一類形式的Jacobian矩陣行列式來判別并聯機構是否處于奇異位形。圖2(a)、圖2(b)分別為作為算例的Stewart并聯機構的位置奇異曲面和姿態奇異曲面。在進行機構的軌跡規劃時,應避開奇異曲面中的全部坐標點。

圖2 Stewart并聯機構的奇異曲面

5 結語

1)用歐拉角及其導數描述動平臺的轉動速度,并選取動坐標系的原點為平動速度基點,可推導出第1類形式的運動Jacobian矩陣。

2)用角速度矢量描述動平臺的轉動速度,并選取動坐標系的原點為平動速度基點,可推導出第2類形式的運動Jacobian矩陣。

3)用角速度矢量描述動平臺的轉動速度,并選取動平臺上與靜坐標系原點重合的點為平動速度基點,可推導出第3類形式的運動Jacobian矩陣。

4)所推導出的3類形式運動Jacobian矩陣的前3列元素完全相同。

5)根據角速度加法公式以及線速度基點法,可建立3類形式運動Jacobian矩陣之間的映射,它們均呈現線性變換的關系。數值算例驗證了上述映射矩陣的正確性。

6)根據矩陣行列式的乘法定理和分塊矩陣的運算規則,可推導出3類形式Jacobian矩陣行列式之間的關系。在不考慮歐拉角奇異點的前提下,它們所對應的機構奇異位形是完全一致的。

7)上述結論為并聯機構的型綜合、型優化提供了理論指導。下一步工作是推導3類形式Jacobian矩陣的特征值、奇異值、條件數之間的關系,以建立并完善6自由度并聯機構的動力學性能指標。