基于RBF神經網絡的柔性機械手反演控制

李正強,劉益軍,賴建防,呂偉宏

(1. 佛山三水供電局,廣東 佛山 528199; 2. 寧波天弘電力器具有限公司,浙江 寧波 315722)

0 引言

近年來機械手的快速發展和應用,推動著整個工業化發展的高效化和智能化[1]。柔性機械手具有速度快、耗能低、接觸面積小等優點,在機器人領域、海洋工程、航空航天領域受到越來越多的重視[2]。

反演控制(backstepping)方法,又稱反步法、回推法或者后推法,形成于1990年初,在此后得到迅速發展并在非線性控制設計取得了很大的成功[3]。反演控制的思想是通過輸入使系統的特性達到李雅普諾夫意義上的穩定,兩者推導上有相似之處,但是思想上還是不一樣的。文獻[4]在拉格朗日動力學基礎上,依據反演控制策略設計滑模控制律,仿真結果表明,所提出的控制方法能夠實現機械手系統快速穩定。為了改善和提高多自由度機械手移動精準度和控制效果,文獻[5]提出了基于自適應滑模的多自由度機械手反演智能控制方法,該方法結合智能感應可以對機械手的期望運動進行軌跡規劃,自適應控制律結合滑模控制方法可以對擾動信號進行補償,進而實現機械手控制系統的穩定。文獻[6]針對在機械手關節位置跟蹤中傳統滑模控制器存在控制輸入抖振和模型受限等問題,提出一種基于新型非線性干擾觀測器的機械手自適應反演滑模控制(SMC)算法。首先,設計干擾觀測器對系統干擾進行觀測和估計,并且在后續滑模控制器設計時進行估計補償;其次,提出自適應反演控制律可以進一步改善機械手控制系統的跟蹤性能。文獻[7]針對不確定機械手系統的軌跡跟蹤控制問題, 提出了一種基于干擾觀測器的機械手收縮反步控制算法。采用非線性觀測器對機械手系統的模型不確定項和未知外部干擾部分進行觀測,將上述提出的控制方法應用于機械手, 通過滑模控制方法和反步法的對比仿真, 證明其有效性。為解決平臺與安裝機器人機械手之間的擾動、非線性、非完整約束和動態耦合問題,文獻[8]介紹了一種基于反步法的自適應滑模控制器,該控制算法依賴于采用反步法來提高全局極限漸近穩定性和應用滑模控制來獲得對不確定性的高響應和不變性,仿真結果證明了其有效性和魯棒性。

系統模型參數變化、建模不確定性以及建模誤差往往會對控制器設計帶來不可忽略的挑戰。文獻[9]提出基于FDO的非線性滑模控制方法, 與此同時,不需要提前知道不確定性的大小,使用自適應方法估計并在后續控制器設計中進行了補償。該方法與其他的非線性SMC相比,系統的控制精度和魯棒性更高。文獻[10]針對多關節機械手在建模過程中存在建模誤差及建模過程中不確定性等問題,提出將神經網絡干擾觀測器思想引入滑模控制器設計中,在無需提前知道不確定性干擾的上界先驗知識,設計神經網絡觀測器對不確定性干擾進行逼近,通過李雅普諾夫進行了穩定性證明,通過MATLAB仿真結果表明該控制算法能夠有效地提高機械手跟蹤控制精度。為了降低機械手運動時存在軌跡偏差,文獻[11]設計了6自由度機械手模型并對末端執行器進行運動軌跡規劃,利用RBF神經網絡訓練離散點,實驗結果表明軌跡優化合理,對機械手生產應用有一定的指導意義。文獻[12]針對欠驅動柔性機械手系統動力學方程難以準確建立、系統性能降低的問題, 通過自適應神經網絡在線對機械手關節進行切換控制,數字仿真驗證了所提出控制策略的有效性。

基于以上文獻分析,本文針對柔性機械手被控對象模型復雜及具有強非線性等情況,提出了一種將RBF神經網絡思想引入反演控制器設計中。設計RBF神經網絡逼近被控對象中模型未知函數,可以對未知函數進行有效地觀測和估計,從而進一步提高柔性機械手控制系統的魯棒性和控制精度。

1 問題描述

1.1 柔性機械手動力學模型

針對機械手系統模型比較復雜的問題,通過合理假設,柔性機械手動態方程可以改寫成

(1)

式中:柔性力臂和電機的轉動角度分別為q1(q1∈Rn)和q2(q2∈Rn);I表示力臂的轉動慣量;K表示力臂的剛度;u表示控制輸入;J為轉動慣量;M為力臂的質量;L為力臂質心到關節點長度。

(2)

1.2 動力學模型變換

為了實現柔性機械手的反演控制,將式(2)進一步改寫成

(3)

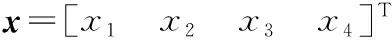
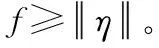
1.3 徑向基函數(RBF)神經網絡

徑向基函數結構簡單、訓練簡潔、學習收斂速度快、能夠逼近任意非線性函數,克服局部極小值問題[13]。

對于在Ω∈R上的未知非線性函數g(x),可利用RBF神經網絡逼近,表示為

g(x)=WTθ(x)+ε

(4)

式中:x∈Ω∈R是輸入向量;W∈Rl是最優權重向量;l>1;ε是固有逼近誤差,滿足|ε|≤εm,其中εm>0為神經網絡逼近誤差的上界;θ(x)=[θ1(x),θ2(x),…,θl(x)]T為平滑向量。徑向基函數一般選擇高斯函數,表達式為

(5)

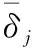
2 反演控制器設計

2.1 基本反演控制器的設計

定義位置誤差e1=x1-x1d, 位置指令x1d=yd。

(6)

定義

e2=x2-x2d

(7)

式中x2d為虛擬控制量。

設計虛擬控制量x2d:

(8)

式中k1>0。

由式(6)和式(8)可得:

(9)

選擇Lyapunov函數如下:

(10)

對V1進行求導可得

(11)

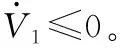
由式(7)可得

(12)

定義

e3=x3-x3d

取虛擬控制量x3d為

(13)

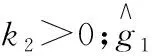
由式(8)可得

(14)

由式(12)和式(13)可得

(15)

設計Lyapunov函數如下:

(16)

對V2進行求導可得

(17)

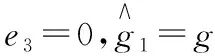
定義

(18)

由式(13)—式(16)可得

(19)

(20)

式中:

(21)

(22)

定義e4=x4-x4d,虛擬控制量x4d設計為

(23)

式中k3>0。

將式(20)—式(23)代入式(18)可得

(24)

選擇Lyapunov函數如下:

(25)

對V3求導可得

(26)

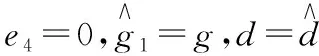
將控制輸入信號引入可得

(27)

則

(28)

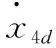
(29)

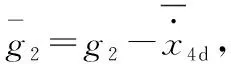
(30)

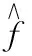
控制律設計為

(31)

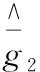
將式(31)代入式(30),可得

(32)

選擇Lyapunov函數如下:

(33)

則

(34)

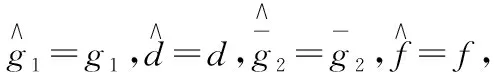
2.2 RBF神經網絡反演控制器設計

(35)

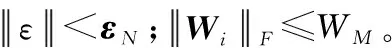
定義

(36)

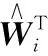
定義

(37)

(38)

選擇Lyapunov函數如下:

(39)

式中:

設計RBF神經網絡自適應律為

(40)

證明:

由式(34)和式(39)可得:

(41)

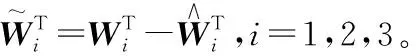
(42)

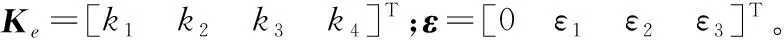
引入自適應律式(40),可得

(43)

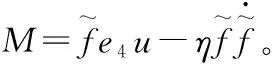
為了保證M≤0,不妨設計自適應律為

(44)

將式(44)代入M,為保證M≤0,需滿足如下3種情況:

1)當e4u>0,M=0;

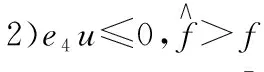
根據Schwarz不等式,有

由于

當滿足如下方程

(45)

式(43)可進一步改寫為

(46)

(47)

(48)

(49)

3 數字仿真分析

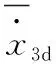
bi=8;網絡的初始權值為0。

在神經網絡自適應控制律式(40)中,選取n=0.01,

J=0.216。

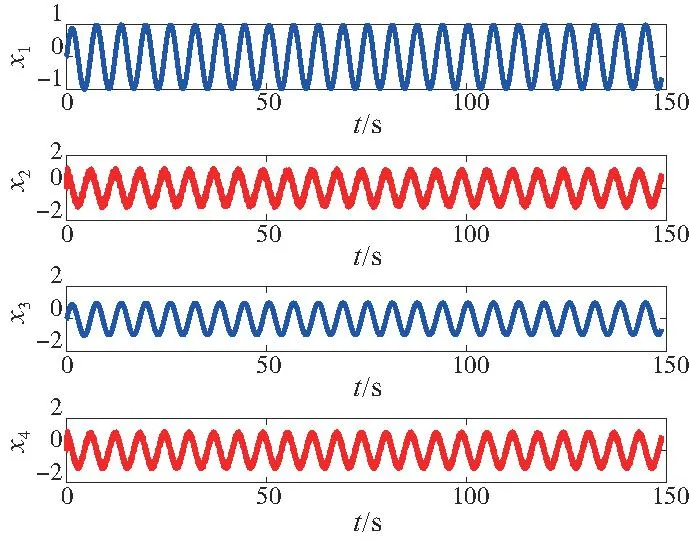
圖1 系統狀態量變化

圖1表示系統的4個狀態變化量x1,x2,x3,x4。圖2為位置跟蹤圖,實線表示給定的指令,虛線代表位置的跟蹤。由圖1和圖2可以看出,系統狀態量穩定且可以很好地跟蹤到給定的指令位置。圖3仿真結果可以看出系統的控制輸入穩定在一定范圍內。由圖4仿真結果不難看出,RBF神經網絡對未知的非線性函數具有很好的逼近效果。

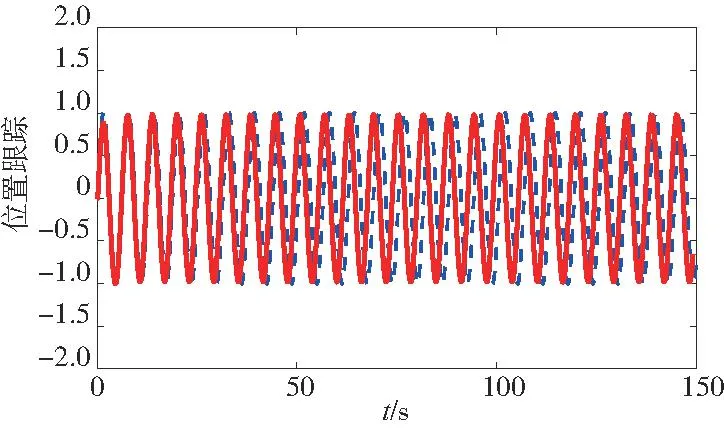
圖2 位置跟蹤圖

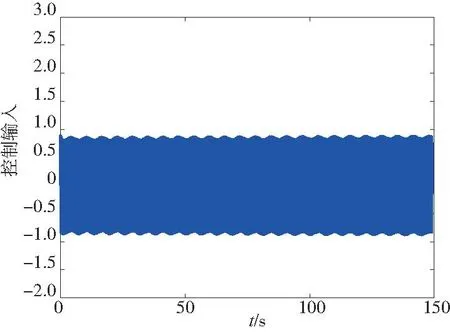
圖3 控制輸入響應曲線

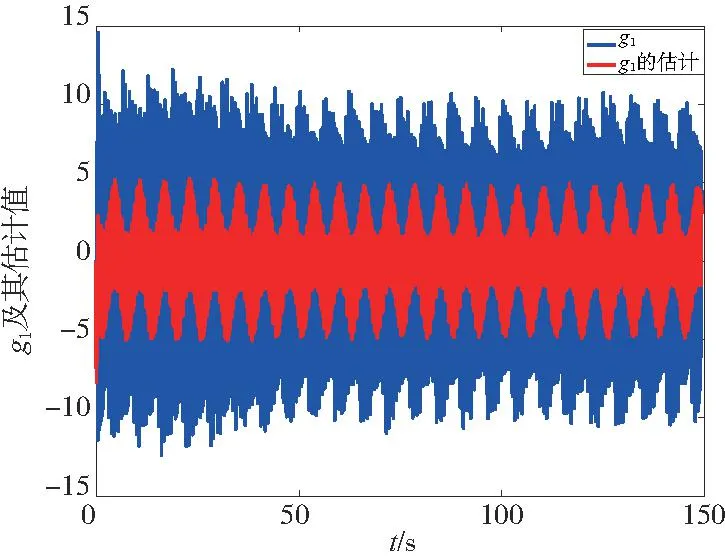
圖4 非線性函數g1及其估計值

4 結語

本文針對被控對象柔性機械手模型復雜及具有強非線性等情況,提出了一種將RBF神經網絡思想引入反演控制器設計中。主要研究內容如下:

1)基于反演控制理論,將原復雜的高階非線性系統分解成低階簡單系統,極大簡化了控制器直接設計的難度;

2)針對被控對象模型中存在的未知非線性函數,設計RBF神經網絡能夠對未知的非線性函數進行很好的逼近,可以有效地提高控制器的性能和魯棒性。

本文選擇合適的仿真參數確保了控制輸入在一定合理范圍,但在實際工程中,控制器輸入往往會存在飽和情況,而在本文控制輸入飽和特性并未考慮進去,在未來的研究中會進一步考慮控制輸入飽和特性,以提高機械手控制系統的魯棒性。