基于數據驅動的大氣壓射頻放電等離子體數值模擬研究1)

王緒成 李文凱 艾 飛 劉志兵 張遠濤

(山東大學電氣工程學院,濟南 250014)

引言

近年來,大氣壓非平衡等離子體的研究得到人們廣泛的關注[1-4],特別是大氣壓下的容性耦合射頻放電由于其結構相對簡單,耦合功率密度高,能產生大體積均勻等離子體等優勢,成為了目前國際上放電等離子體領域的熱點研究之一[5-7].一直以來,射頻放電等離子體在等離子體刻蝕、鍍膜和生物醫學等方面得到了廣泛的應用[8-10].大量的實驗和計算研究表明大氣射頻放電可以工作在不同的放電模式下,即α 模式和γ 模式[11-13].在α 模式下,大氣壓射頻放電可以產生均勻的大體積等離子體,但當輸入功率增加時,這種均勻的等離子體很容易出現氣體加熱效應,并呈現徑向集聚,導致射頻放電從α 模式過渡到γ 模式[14-15].因此需要深入研究抑制大氣壓射頻放電模式轉換的方法,一般說來降低放電間隙至微等離子體尺度與提高放電頻率至甚高頻范圍是常用的抑制手段,引入脈沖調制也是近年發展起來的有效方法[16-17].

數值模擬作為揭示放電等離子體物理特性的一種有效方法,已被證明是探究大氣壓射頻放電中各種物理和化學特性的有效工具,目前常用的等離子體數值模擬方法包括粒子(PIC-MCC)模擬與流體模擬[18-19].粒子模型在整個模擬過程中追蹤了放電空間內所有的宏粒子位置與速度的變化以及電場的變化,可以詳盡地描述等離子體放電過程中的動理學特征.流體模型通過數值求解帶電粒子的連續性方程、動量方程和能量方程,并耦合泊松方程對放電的發展進行模擬.但是在大氣壓下,當放電空間尺度非常小(比如微等離子體),時間尺度變化非常快(比如ns 脈沖放電)時,流體模擬無法準確地描述等離子體的動理學特性.但是粒子模擬對于大氣壓高密度等離子體以及密度范圍變化較大的放電過程的計算耗時極大.總的來說,流體模型并不適于微間隙條件下的等離子體建模研究,而粒子模型則在苛刻的時間步長與空間步長條件限制下需要極大的計算耗時[19],因此引入一種新的計算模式來提高數值模擬的效率與效果是非常必要的.

近年來,由于等離子體研究和應用領域中數據科學和技術的進步,數據驅動的等離子體科學和技術正在迅速發展[20].數據驅動的科學被稱為發現的第四范式,數據驅動的發展使通過人工智能實現完全自動化的科學發現成為可能[21].在數據驅動技術中,人工神經網絡已經成為實現具有非線性特征的輸入-輸出映射系統建模的強大手段[22-25].人工神經網絡學習復雜映射的固有能力,以及相對容易訓練的特性,可能使其非常適合基于非線性模型的等離子體建模工作.此外,神經網絡可以從訓練數據中學習等離子體系統的性質,進而給出反映等離子體特性的數據,實現從輸入數據到輸出數據的映射,而無需事先了解等離子體性質背后的物理方程[26].

一般來說,人工神經網絡由輸入層、隱藏層和輸出層組成,當隱藏層的個數超過兩個時,可以將該神經網絡稱為深度神經網絡(deep neural network,DNN).目前,DNN 已成功地被應用于各種等離子體過程.我們曾基于機器學習方法構造了一個DNN 來探究大氣壓介質阻擋放電的電流電壓特性、電場強度和帶電粒子密度等宏觀與微觀放電特性[27],該研究表明DNN 是研究大氣壓等離子體特性的有力工具.Pan 等[28]將DNN 引入到等離子體催化動力學建模中,他們使用DNN 代替動力學模擬,有效地預測了不同約化場下目標產物的密度.此外,Nazari 等[29]開發了一個神經網絡來評估介質阻擋放電反應器中CO2的轉化率和能源效率.計算結果表明,神經網絡在評估等離子體輔助CO2轉化性能方面具有極大的潛力.可以這樣講,基于數據驅動技術的DNN 算法不僅可以自動提取訓練數據的特征,而且在滿足精度要求的前提下具有很高的計算效率,這為低溫等離子體數值模擬提供了一種很有潛力的方法.

因此,本研究以DNN 在大氣壓射頻放電中的計算為例,討論數據驅動方法在低溫等離子體模擬中的應用.相較于我們之前研究的大氣壓介質阻擋放電[27],大氣壓射頻放電由于放電頻率較高,帶電粒子一般被束縛在放電空間內,所以放電電流及帶電粒子密度在一個周期內變化比較平緩.在本研究中,我們基于數據的特點,構建了一個具有多層隱藏層的通用DNN 結構,并利用該DNN 模型代替流體模型和粒子模型,實現對于大氣壓射頻放電等離子體的各種動理學特征的準確高效計算.

本文的主要內容如下: 第1 節簡單描述了用于提供訓練數據的流體模型和粒子模型,并構造了一個適用于預測大氣壓射頻放電特性的通用型DNN算法;在第2 節中通過將DNN 模型的預測結果與傳統的流體模型及粒子模型的計算結果進行比較,證明了DNN 模型的高效性和準確性,同時使用該DNN 模型對大氣壓射頻等離子體的各種特性進行了高效的分析研究;最后,第3 節給出了本工作的總結和展望.

1.1.1 流體模型

在大氣壓下,帶電粒子的平均自由程非常短,粒子之間的碰撞也非常頻繁.在射頻放電的研究中,流體模型通常用連續方程和擴散漂移近似方程來描述各種粒子的產生、消失與輸運,使用泊松方程計算放電空間中的電場強度,基于麥克斯韋分布的假設,通過求解電子能量平衡方程來獲得電子溫度.因此,描述大氣壓射頻放電的主要控制方程如下[30-31]

1 計算方法描述

1.1 物理模型

式中,下標i表示粒子i,N,Γ和S分別表示粒子數密度、粒子通量和粒子源項,μ和D分別為粒子遷移率和擴散系數.qi表示粒子i的電荷量(例如電子的電荷量為-1).ε0和E分別為真空介電常數和電場.,e,me,mg,kel,kB,Te和Tg分別表示電子平均能量、基本電荷、電子質量、背景氣體分子質量、背景分子與電子之量間的動量傳遞頻率、玻爾茲曼常數、電子溫度和氣體溫度.具體的流體模擬方法的示意圖如圖1 所示.只是需要注意的是,大氣壓下極其頻繁的粒子碰撞嚴重限制了流體模擬中空間網格和時間步長的選擇.

圖1 流體模擬方法Fig.1 Scheme of the fluid simulation

1.1.2 粒子模型

對于大氣壓射頻放電,特別是在微間隙中,電子能量分布函數(EEDF)并不一定滿足Maxwell 分布,另外在大氣壓射頻放電從α 模式轉化到γ 模式過程中,等離子體的動理學行為有時也較為顯著,這樣,粒子模擬就成為必需的數值模擬方法.

在粒子模型中,為了避免數值不穩定導致的模擬發散,必須選擇合理的時間步長和空間步長,即Δx≤λD,ωpΔt≤2 和Δx/Δt≤vt,其中λD是等離子體德拜長度,ωp是等離子體振蕩頻率,vt是電子熱速度[32].在粒子模擬的過程中為了保證準確地計算粒子運動軌跡,要求運動方程的積分時間步長必須足夠小,需要成百數千個的粒子網格,而時間步長往往被限制在10-14～ 10-12s 之間.另一方面,空間分辨率的選擇是準確描述等離子體動理學特征的關鍵,每個網格內需要超過100 個宏粒子以消除蒙特卡羅過程的隨機誤差[33].在粒子模擬的具體實現中,隱式格式可以在保持計算精度的同時盡可能地允許更大的時間步長和空間步長,從而可以大幅提升計算效率[34].一般說來,粒子模擬循環過程如下: (1)計算帶電粒子密度;(2)計算電勢和電場;(3)計算作用在粒子上的力;(4)推進粒子;(5)在邊界上添加或移除粒子;(6)執行碰撞過程.如圖2 所示.

圖2 粒子模擬方法Fig.2 Scheme of the PIC-MCC simulation

可以說,描述低溫等離子體的粒子模型與流體模型的主要物理方程是相對明確的,可以通過不同的數值方法求解這些物理方程,比如根據需要選擇使用有限元、有限差分及邊界元等數值方法來實現;即使使用相同的數值方法,所采用的具體算法也可以是不同的,如求解漂移擴算近似的SCG 算法與ISG 算法等.因此,粒子模擬與流體模擬的數值實現方式通常是比較多樣性的.

1.2 數據驅動模型

基于對大氣壓射頻放電的理解,特別是對其動理學特性的深入分析,本文構建了一個具有4 層隱藏層的DNN,如圖3 所示.該DNN 是一個基于TensorFlow平臺開發的具有GPU 加速的全連接多層反向傳播神經網絡,由輸入層、隱藏層和輸出層3 層結構組成,每個隱藏層內有30 個神經元.該DNN 網絡結構是經過隱藏層層數、神經元個數以及激活函數的各種組合試驗而得到的.一般來說,增加隱藏層層數可以增加網絡的表示能力和學習能力,每一層隱藏層都可以學習到數據的不同抽象特征,這些特征逐層組合可以形成更高級和復雜的特征表示.增加神經元個數能夠增加每個隱藏層的表示能力,提供更多的自由度,使網絡能夠學習到更復雜的函數映射.但隨著DNN 隱藏層層數和神經元數量的增加,網絡的參數量和計算復雜性也會隨之上升,導致訓練時間增加.本文所構建的DNN 是通過反向傳播算法來更新網絡參數的,而深層網絡在反向傳播過程中可能面臨梯度消失或梯度爆炸的問題,這可能導致訓練過程變得困難.特別是在訓練數據有限的情況下,DNN 可能會過度依賴訓練數據中的噪聲或不重要的特征,導致過擬合問題的出現.在對DNN 結構的不斷調整中發現,在探究一維射頻放電特征時,增加隱藏層的層數和神經元的個數都會導致訓練時間的明顯提升.與增加神經元個數相比,增加隱藏層的層數更能明顯提高訓練準確度,但是當隱藏層層數過多時,提升效果將不再明顯.

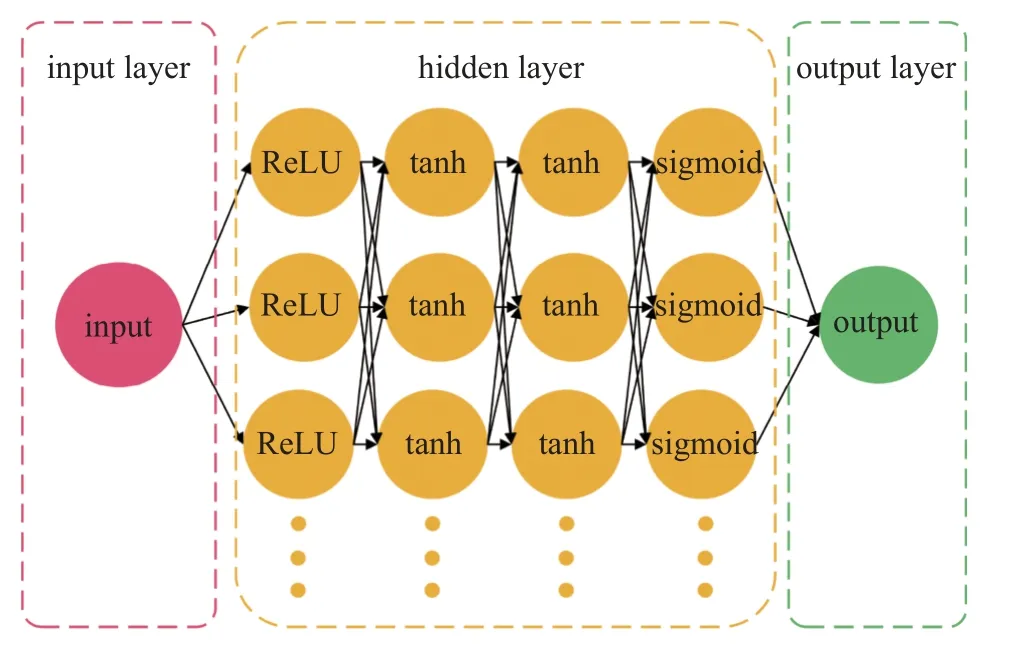
圖3 基于大氣壓射頻放電特性構建的DNN 示意圖Fig.3 Schematic of DNN constructed based on the characteristics of atmospheric RF discharges

進一步說,由于DNN 處理的對象是數據,因此DNN 的隱藏層層數、神經元個數及激活函數等參數是由數據的特點決定的.比如有的數據變化比較劇烈(數據梯度大),而有的數據變化比較平緩,這就需要對隱藏層的層數與神經元的個數進行調整,使模型訓練時間及預測精度之間達到某種平衡.一般說來,低溫等離子體數據的特點是由相應放電的物理性質來決定的,比如本文研究的射頻放電,其電流電壓的變化是連續的、比較平緩的,而另一種常用的大氣壓脈沖放電的電流則是近乎突變的、非常劇烈的.顯然這兩種放電所產生的電流數據具有不同的特點,因此需要對DNN 結構做出相應的調整.本文研究大氣壓射頻放電的DNN 中將隱藏層層數設置為4 層,每層的神經元數目設置為30 個,4 個隱藏層中依次采用ReLU 函數、tanh 函數、tanh 函數和sigmoid 函數作為激活函數.首先,ReLU 函數能夠高效地映射放電特性的突變;其次,采用兩個tanh 函數能夠實現對放電特性的進一步擬合,達到較好的預測精度;最后,使用sigmoid 函數對預測曲線進行平滑處理[35].該DNN 的輸入參數為放電條件(如電壓幅值、驅動頻率和放電間隙等),輸出為大氣壓射頻放電的各種物理量,例如電場強度、產物粒子密度和電子溫度等.

實際上,具有J層神經網絡的DNN 的輸入輸出關系映射可以表示為

式中,Yout和Xin分別表示DNN 輸出層的輸出和輸入層的輸入;和Yj分別表示第j層神經元的前饋傳遞函數及其輸入;θ=｛W,b｝為DNN 訓練過程中需要被優化的參數,W和b分別為權重和偏置;σ為激活函數.DNN 通過權重W、偏置b以及激活函數σ將每層神經網絡相互連接,DNN 的訓練就是通過不斷地優化θ=｛W,b｝,逐步逼近DNN 的輸入-輸出映射關系,從而使得DNN 的輸出結果接近于訓練集中的給定值.可以說,DNN 通過建立輸入輸出特征量之間的映射關系,將數值模擬中控制方程的求解轉化為不斷更新權重和偏置參數的優化學習算法,這極大提高了放電等離子體數值模擬的計算效率.在本工作中,經過訓練以后的DNN 可以通過式(5)和式(6)根據輸入的放電參數直接獲得相應的放電特性.

在DNN 的訓練過程中,將標準差函數(MSE)作為DNN 的損失函數,并使用優化器Adam 最小化該損失函數以獲得最優的權重W和偏置b.標準差函數表示為

式中,Ndata表示計算域中所包含的采樣點的數量;ys為數值模擬的計算結果,而yp則是DNN 模型的預測結果.此外,在DNN 的驗證過程中,采用平均相對誤差(MRE)來直觀地描述預測數據與模擬數據之間的差異

圖4 進一步總結了基于數據驅動技術的DNN算法的基本過程.首先,將數值模擬(或實驗診斷)得到的數據分為訓練集和測試集.這兩個數據部分彼此相互獨立,其中訓練集主要是用來訓練DNN 模型中的參數,一般來說要求其能涵蓋樣本空間,即整個放電參數范圍內的所有的信息;測試集用于判斷DNN模型的預測性能.如果在測試集內DNN 的預測結果滿足要求,則表明該DNN 在給定參數范圍內具有良好的泛化性能.隨后,通過TensorFlow 自帶的命令導出DNN 模型參數,在DNN 的預測過程中只要預加載模型參數后按照模型的輸入層結構輸入放電參數,就可以迅速獲得相應的放電物理量.需要特別指出的是,隨著人工智能技術的發展,針對低溫等離子體的物理特點以及研究的目的,更多新興的數據驅動方法將會被引入到低溫等離子體的研究中[36-38],上述DNN 只是常用的一種神經網絡模型.

圖4 基于數據驅動技術的DNN 算法示意圖Fig.4 Schematic diagram of DNN algorithm based on data-driven method

需要澄清的是,以DNN 為代表的數據驅動方法能夠高效地給出某特定單一物理信息,比如DNN 可以分別單獨給出電場強度、粒子密度和電子能量分布函數(EEDF)等放電特性;而傳統的粒子模型和流體模型等物理方程驅動的模擬方法則可以一次性給出包含全部物理信息的數據.一般說來,DNN 對于單一放電物理量預測的訓練所需要的時間從幾十分鐘到幾小時,但是訓練后給出相應的物理信息則只需要0.01 s,這對于需要進行實時監測、反饋并調整的等離子體系統是非常重要的,比如與等離子體醫學相關的精準醫療過程[39].

如圖4 所示,也可以將單一放電物理量輸出的DNN 訓練后進行耦合,實現對于多個放電物理量的快速預測.本工作所構建的DNN 模型本質上也支持多放電參數的輸入和多物理量的輸出,其維度可以由用戶自定義,但是多參數的輸入輸出必然會導致DNN 的訓練集數據需求量和訓練時間的增加,這對計算平臺的計算能力構成了巨大的挑戰.

需要進一步說明的是,DNN 所需要的數據可以來自于數值計算,當然也可以來自實驗診斷.對于DNN 而言,主要關注的是訓練數據的數量與質量,當然在知道其來源的情況下,可以有針對性地調整DNN 的構建,以便在給定數據的情況下獲得更好的訓練和預測效果.比如正在興起的小樣本學習技術,為基于實驗數據進行DNN 的訓練研究等離子體性質提供了極大的方便[40-41].

2 結果分析與討論

2.1 基于數據驅動研究大氣壓射頻放電演化特性

在本節中,使用流體模擬獲得的計算數據訓練DNN 以實現對于大氣壓射頻放電演化特性的高效研究.在這里將輸入電流密度和電極間距作為DNN的輸入,研究二者對α 和γ 模式下大氣壓射頻放電特性的影響.在流體模型中,大氣壓射頻等離子體在兩個對稱的平行板電極之間產生,放電氣體為純氦氣.正弦形式的電流密度I=I0sin(2πft)被視為流體模擬的輸入,其中I0是電流幅度,f是驅動頻率.在本節中,驅動頻率被固定為13.56 MHz.大氣壓氦氣等離子體中考慮了電子(e)、兩種離子(He+和He2+)、兩種亞穩態粒子(He*和He2*) 以及背景氣體氦氣(He).模型中詳細的化學反應和相應的反應速率系數可從參考文獻[42]中獲得.

在本節中,選取315 組電流密度有效值(RMS電流密度)在0～ 85 mA/cm2之間、電極間距在1.6～3.2 mm 之間的流體模擬數據作為預測電流電壓特性的訓練數據集,共包含約117 萬個時間采樣點.選取280 組RMS 電流密度在10～ 85 mA/cm2之間,電極間距在1.6～ 3.2 mm 之間的時均電子密度、離子密度、電場和電子溫度空間分布的模擬數據作為預測電子密度、離子密度、電場和電子溫度的訓練數據集,共有約67 萬個空間采樣點.需要說明的是,在DNN 的訓練過程中,訓練集數據的質量對DNN 模型的預測精度和訓練速度有著極大的影響.數據量較少的訓練集可能會導致DNN 模型的預測精度達不到要求;而如果訓練集中包含了太多的數據量,則會提高數值模擬的計算和DNN 訓練的時間成本.因此選擇合適的訓練集數據對于DNN 模型在放電等離子體中的應用是至關重要的,這與數據本身的特點及所需的預測精度等因素都有關.

經過訓練以后,在測試集中DNN 的預測結果與流體模擬結果吻合良好,各種放電特征量的平均相對誤差均小于0.5%.為了說明DNN 預測的有效性,下文展示了電極間距為2.4 mm、RMS 電流密度分別為30 mA/cm2(α 模式)和80 mA/cm2(γ 模式)時DNN 預測的放電特性與流體模擬結果的對比.圖5(a)和圖5(b)分別給出了當驅動頻率為13.56 MHz時,在α 和γ 模式下DNN 預測的時均電子密度、離子密度和電場的空間分布,并與流體模擬的結果進行了比較.圖5 中的虛線和實線分別代表DNN 預測結果和流體模擬結果.如圖5(a)所示,當RMS 電流密度為30 mA/cm2時(即放電工作在α 模式下),電子和離子聚集在體等離子體區,其密度最大值出現在放電空間的中心區域.而在鞘層區域,離子密度高于電子密度,形成空間電荷區,導致強電場區域的出現.

圖5 DNN 預測的α 和γ 模式下的時均電子密度、離子密度和電場的空間分布與流體模擬結果的比較Fig.5 Spatial distributions of time-averaged electron density,ion density,and electric field in the α mode and the γ mode predicted by DNN with comparison of the results obtained from the fluid simulation

此外,圖5 中DNN 預測的電子密度、離子密度和電場的平均相對誤差分別為0.17%,0.11%和0.39%,這表明DNN 的預測具有較好的精度.在圖5(b)中,當輸入電流密度為80 mA/cm2時,射頻放電工作在γ 模式.此時,鞘層區域的電場強度較大,大量的帶電粒子在鞘層區域產生.這說明在γ 模式下,電離主要由鞘層區域電子雪崩主導.此外,在γ 模式下,DNN預測的電子密度、離子密度和電場與流體模擬結果之間的相對誤差分別為0.06%,0.03%和0.43%.這意味著無論是在α 模式還是γ 模式下,DNN 都能實現對于大氣壓射頻放電中帶電粒子密度和電場強度空間分布的準確預測.

同時,圖6 給出了RMS 電流密度分別為30 mA/cm2(α 模式)和80 mA/cm2(γ 模式)時的DNN 對于時均電子溫度空間分布的預測,并與相應的流體模擬結果進行了比較.從圖6 可知,DNN 對α 和γ 模式下大氣壓射頻放電中的電子溫度也具有很好的預測能力.在α 和γ 模式下,DNN 預測的電子溫度的平均相對誤差分別為0.07% 和0.05%.與α 模式相比,γ 模式下的電子溫度沿電極間隙的降低更加明顯.這是因為在γ 模式下,電子在鞘層強電場加速,從而在鞘層內獲得較高的能量,同時鞘層內部與邊緣的碰撞頻率上升,消耗了一定的能量,導致等離子體區的電子溫度較低.

圖6 DNN 預測的α 和γ 模式下的時均電子溫度的空間分布與流體模擬結果的比較Fig.6 Spatial distributions of time-averaged electron temperature in the α mode and the γ mode predicted by DNN with comparison of the results obtained from the fluid simulation

圖5 和圖6 表明,經過訓練后的DNN 能夠準確描述大氣壓射頻放電的關鍵特性,如電場分布、帶電粒子密度及電子溫度分布等,預測結果與模擬結果表現出很好的一致性,其相對誤差均小于0.5%.更為關鍵的是,與傳統的數值模擬方法相比,DNN具有極高的計算效率.一般來說,基于流體模型獲得的訓練數據,DNN 在經過大約1 h 的訓練后就可以實現對于某一放電特征量的精準預測.對于給定參數范圍內的任一參數輸入,DNN 得到某一放電特征量的真實計算時間僅為0.01 s.而在一維流體模型中,基于(improved Scharfetter-Gummel,iSG)方法[43],流體模型需要運行至少3000 個射頻周期才能確保大氣壓射頻放電達到穩態,在給定的計算平臺下(Intel Core i7-12700 F CPU,16 GB RAM),這大約需要2000 s.與傳統的流體模擬相比,經過訓練后DNN 計算效率提高了約105倍.可以說,DNN 的應用幾乎實現了大氣壓下射頻放電特性的實時預測.此外,經過訓練后的DNN 能夠以極高的精度迅速得到給定參數范圍內的任一放電參數下的大氣射頻放電的特性,這將為大氣壓射頻放電特性的研究提供足夠多的數據,有利于進一步研究大氣射頻等離子體的演化行為.

在經過有效性驗證后,使用該DNN 對輸入電流密度和電極間隙對大氣壓射頻放電特性的影響進行討論.如圖7 所示,經過訓練后的DNN 能夠以曲面的形式在1 s 內給出不同電極間距下的大氣壓射頻放電的電流電壓特性,其中黑色虛線和綠色虛線分別表示不同電極間距下的大氣壓射頻放電的擊穿電壓和α-γ 模式轉變點.根據DNN 的預測,當電極間距從1.6 mm 增加到3.2 mm 時,擊穿電壓的有效值從148.1 V 增加到270.5 V.擊穿電壓隨電極間距的增加而增加,這與實驗測量結果定性一致[15].在圖7中,等離子體的微分電導率由正變為負的點被認為是α-γ 模式轉變點.當電極間距從1.6 mm 增加到3.2 mm 時,模式轉變點的氣體電壓從448.1 V 增加到497.6 V.當間隙寬度較小時,射頻放電在模式轉換點之前的需要的放電維持電壓更低,這意味著降低電極間距有利于提高大氣壓射頻等離子體的穩定性.

圖7 DNN 預測的不同電極間距下大氣壓射頻放電的電流-電壓特性Fig.7 Current-voltage characteristics of atmospheric RF discharges predicted by DNN for various electrode spacings

一般說來,基于實驗數據與流體模型給出的伏安關系往往是分離的曲線,每一條曲線上的數據點個數也是有限的[5,31],而基于DNN 的計算則可以近乎實時地給出一個伏安特性曲面,如圖7 所示,從而將伏安特性隨放電間隙的變化更為明確地表現出來,擊穿電壓與放電模式轉化電壓的演化規律也更加清晰.可以說,DNN 能夠實時給出任意間隙的伏安特性曲線.即,由于極高的計算效率,DNN 可以極大地豐富和強化計算結果,這也是數據驅動技術應用于低溫等離子體模擬的重要優勢.

如圖8(a)和圖8(b)所示,DNN 也可以迅速給出不同輸入電流密度和電極間距下的電子和離子的最大時均密度曲面.基于給定的計算平臺,DNN 只需不到1 s 的時間就可以獲得圖8 中的最大帶電粒子密度曲面.從圖8 中可以看到,電子和離子的密度隨輸入電流密度和電極間距的增大而增大,當RMS 電流密度為85 mA/cm2、電極間距為3.2 mm 時,電子和離子的密度均達到最大值8.38 × 1011cm-3.這表明在較大的輸入電流密度和電極間距下大氣壓射頻放電能夠產生更多的帶電粒子.

圖8 DNN 預測的不同RMS 電流密度和電極間距下的最大時均電子密度和離子密度Fig.8 The maximum time-averaged electron density and ion density predicted by DNN as a function of both the RMS current density and electrode spacing

2.2 基于數據驅動模型研究射頻微放電動理學特性

在大氣壓射頻放電中,增加驅動頻率和減小電極間隙被認為是產生均勻的大體積等離子體的有效方法[15,44].然而,隨著放電間隙減小至幾百微米量級,等離子體的空間尺度已經可以與等離子體的德拜長度相比擬,等離子體集體效應不再顯著,同時微間隙下一般具有較強的電場,導致等離子體呈現出明顯的動理學特性[10].本節借助于粒子模型來討論射頻微等離子體特性,并基于粒子模擬計算得到的結果訓練DNN 以探究驅動頻率對大氣壓射頻微放電中以EEDF 為代表的動理學特性的影響.

在粒子模擬中,大氣壓射頻放電采用了平行板電極結構,并且由正弦電壓V(t)=V0sin(2πft)驅動,其外加電壓幅值V0為300 V,電極間距固定為570 μm.模型中在邊界上考慮了二次電子發射過程,為了簡化計算,固定二次電子發射系數為0.1.在本節中,選取86 組驅動頻率在55～ 905 MHz 之間的粒子模擬數據組成訓練數據集.

首先通過與粒子模擬結果的對比來驗證DNN代替粒子模型探究大氣壓射頻微放電動理學特性的可行性.下文中將以驅動頻率為100 MHz 時的DNN預測結果和粒子模擬結果的對比為例說明DNN 的有效性.圖9 給出了DNN 預測的大氣壓射頻微放電的電場空間分布與粒子模型計算所得到的結果對比.從圖9 中可以很明顯地觀察到,經過良好訓練的DNN 所預測的電場空間分布與粒子模型的計算結果高度吻合,即使是在電場的變化較為劇烈的鞘層區域中兩者的相對誤差也非常小.在圖9 中,DNN所預測的鞘層電場峰值分別為-15.24 和15.27 kV/cm,與粒子模型計算結果的相對誤差僅為0.05%.而從計算效率的角度出發,粒子模型從模擬放電的開始到穩定階段大約需要3.6 × 105s,而經過良好訓練的DNN 模型僅需0.01 s 左右就能以近乎相同的計算精度得到放電空間內的電場分布,計算效率提高了近7 個量級.

圖9 DNN 預測的大氣壓射頻微放電中電場空間分布與粒子模擬結果的比較Fig.9 Spatial distribution of electric field predicted by DNN in atmospheric RF micro-discharge with comparison of the result obtained from the PIC-MCC simulation

圖10 中給出了驅動頻率為100 MHz 下DNN預測的電子密度空間分布與粒子模型計算結果的對比.從圖10 可以看出,DNN 對于大氣壓射頻微放電的電子密度也具有很好的預測能力.當驅動頻率為100 MHz 時,電子密度的空間分布呈現為一個以體等離子體區為主導的單峰分布結構,電子大部分集中在放電空間的中心區域,而電極兩側鞘層區域的電子密度較低.此外,DNN 對于電子密度預測的耗時也僅為0.01 s,這進一步說明了DNN 模型預測大氣壓射頻放電等離子體特性的高效性.

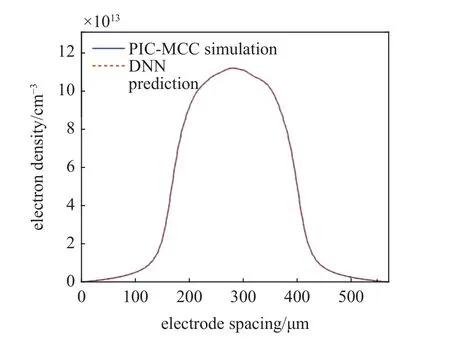
圖10 DNN 預測的電子密度空間分布與粒子模擬結果的比較Fig.10 Spatial distribution of electron density predicted by DNN with comparison of the result obtained from the PIC-MCC simulation

圖11 中給出了DNN 預測的驅動頻率為100 MHz時大氣壓射頻微放電的EEDF,并與粒子模擬的計算結果進行比較.從圖11 中可以觀察到DNN 預測和粒子模擬的計算結果近乎一致,兩者的相對誤差僅為0.03%.由于不同能量的電子加熱過程的差異以及大氣壓下射頻放電的非平衡特性,此時的EEDF呈現一個三溫度分布結構,這種分布與低壓放電中常見的Maxwell 分布、bi-Maxwell 分布和Druyvesteyn分布形成對比.

圖11 DNN 預測的EEDF 與粒子模擬結果的比較Fig.11 EEDF predicted by DNN with comparison of the result obtained from the PIC-MCC simulation

在圖11 中可以觀察到3 種電子基團: 低能電子(電子能量≤2 eV)、中能電子(2 eV＜電子能量＜20 eV)和高能電子(20 eV≤電子能量),其中2 eV 閾值由鞘層坍塌過程中的限制電位的最小值設定.而中能電子與高能電子之間的20 eV 的分界線則是對應于氦原子的激發閾值[45].此外,在EEDF 中高能尾部部分存在一個明顯的“拐點”,這是由于電子在非彈性碰撞范圍內較快的能量弛豫所導致的結果.

以上結果表明,經過良好訓練的DNN 模型可以快速而準確地描述大氣壓射頻微放電的電場空間分布與電子密度空間分布,以及EEDF 等動理學特性.隨后,訓練好的DNN 將用于探究大氣壓射頻微放電的頻率特性.與傳統的粒子模型相比,DNN 將計算時間從幾十小時減少到了0.01 s.DNN 作為一種新型的計算工具顯著提高了大氣壓射頻放電等離子體的計算效率,可以得到更多的數據以更好地體現放電特性的演化規律.

在圖12 中,選取DNN 預測的8 組不同驅動頻率下的EEDF 曲線進行定量分析.從圖12 中可以觀察到,當驅動頻率為100 MHz 時,EEDF 曲線呈現一個典型的三溫度分布特征,而隨著驅動頻率逐漸增加至800 MHz,EEDF 曲線逐漸過渡為麥克斯韋分布.通過對圖中的EEDF 曲線沿電子能量進行積分計算可以得到低能電子、中能電子和高能電子在每個EEDF 曲線中的占比.如圖12(a)所示,當頻率為100 MHz 時,低能電子和中能電子的占比分別為92.83% 和7.08%;當頻率增加至圖12(d) 所示的400 MHz 時,低能電子占比降為80.29%,而中能電子占比升高為19.65%;當頻率進一步增加至圖12(h)所示的800 MHz 時,低能電子占比下降為62.02%,中能電子達到了37.92%.在相同電壓下條件下(注意不是相同功率條件),隨著驅動頻率的增加,低能電子將被加熱,從而使放電空間內的低能電子占比降低而中能電子占比升高,導致EEDF 曲線的低能電子區域逐漸向中能電子區域演化.

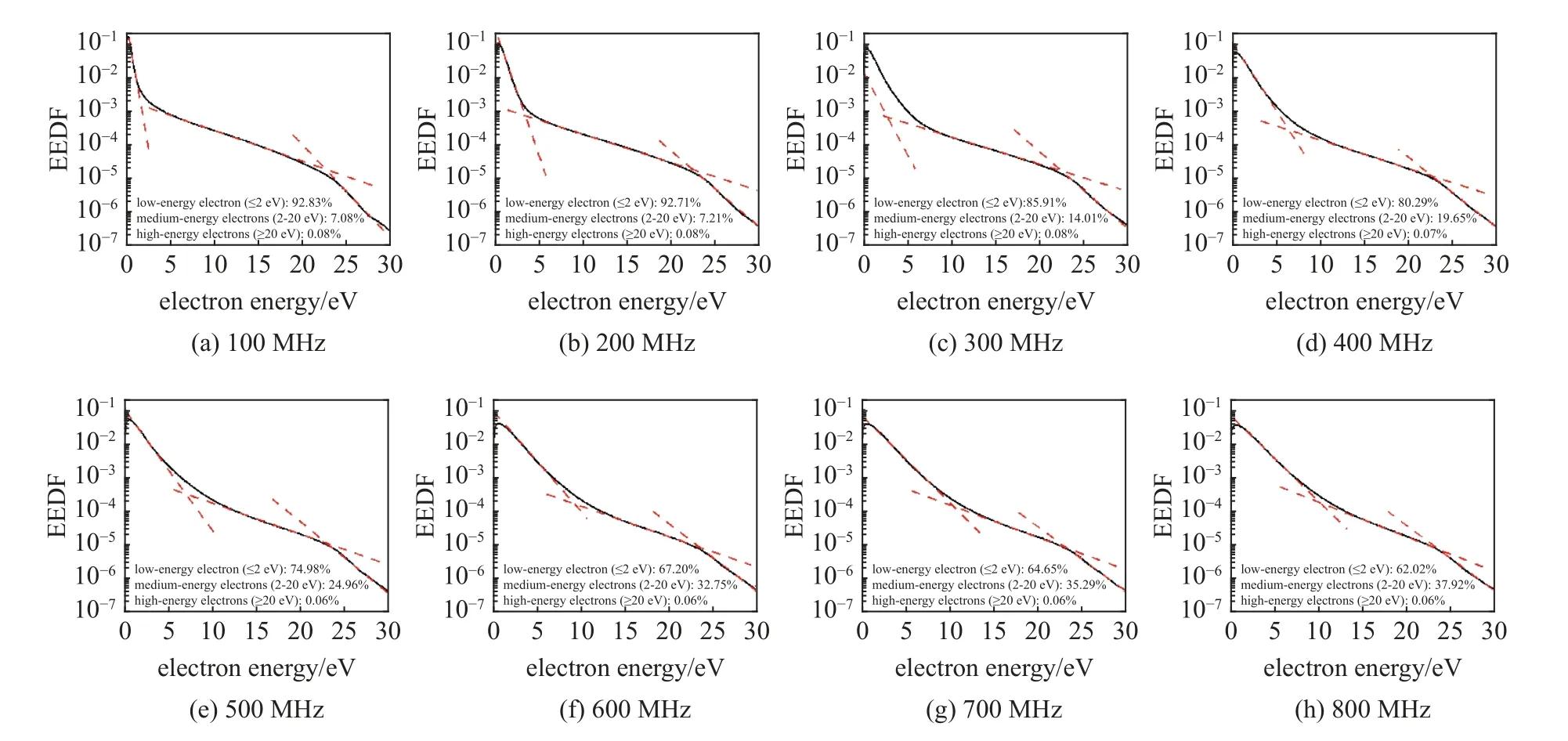
圖12 DNN 預測不同驅動頻率下的EEDF 曲線Fig.12 EEDF predicted by DNNs with various driving frequencies

在大氣壓射頻微放電中,低能電子在整個射頻循環周期內被雙極電勢捕獲并被體等離子體區中較弱的電場加熱.而中能電子主要由鞘層中二次電子的雪崩效應所產生,除了在射頻周期中發生能量弛豫而逐漸失去能量外,在鞘層坍塌時中能電子也會進入電極而消失,因此中能電子并不會存在于整個射頻周期內.另外,鞘層內部分來自介質表面的二次電子能夠在鞘層區域獲得很大的能量,形成高能電子,這些構成了EEDF 曲線中的高能尾部;但由于大氣壓射頻放電的高碰撞性,這些高能電子突破鞘層進入體等離子體區后缺少足夠強的電場對其進行持續的加熱,最終也會在幾十皮秒內發生弛豫而最終失去能量.由于電子的能量弛豫時間明顯地短于射頻周期,因此EEDF 曲線在大氣壓射頻放電中很容易受到頻率的影響.綜上所述,在大氣壓射頻微放電中隨著驅動頻率的增加,低能電子將逐漸轉化為中能電子,而EEDF 曲線也將由三溫度分布向Maxwell分布而過渡.因此,借助于DNN 可以深入細致地揭示大氣壓射頻微等離子體的動理學特性.

進一步,基于DNN 極高的計算效率,圖13 給出了DNN 預測的大氣壓射頻微放電中驅動頻率變化時的EEDF 演化曲面圖.DNN 只需要1 s 左右的時間就能獲得圖13 所示的EEDF 三維圖,清晰地給出EEDF 隨驅動頻率的連續變化.從圖13 中可以觀察到,隨著驅動頻率的增加,低能電子部分呈現一個較為明顯的下降趨勢.在頻率較低時,EEDF 曲線為一個明顯的三溫度分布.隨著頻率的增加,EEDF 曲線變得更加平滑,由三溫度分布逐漸地向Maxwell 分布過渡.而若要從粒子模擬中獲得同樣的大量數據,則至少需要幾百小時的計算時間.這再次說明,基于DNN 的計算可以快速給出海量數據以強化展示模擬效果.

圖13 DNN 預測的大氣壓射頻微放電中EEDF 的頻率演化趨勢Fig.13 EEDF predicted by DNN in atmospheric RF micro-discharge with various driving frequencies

3 結論與展望

本研究以DNN 在大氣壓射頻放電等離子體中的計算為例,討論了數據驅動方法在低溫等離子體模擬中的應用.在這項研究中,將流體模擬和粒子模擬獲得的計算數據作為DNN 的訓練數據.通過將預測結果與數值模擬結果進行比較,驗證了DNN 預測大氣壓射頻放電特性的可行性.對于DNN 自身結構的構建而言,需要綜合考慮預測精度、訓練時間及訓練集數據量等因素.本研究中,在通常的計算工作站上經過大約1 h 的訓練后,DNN 只需要約0.01 s即可獲得大氣壓下射頻放電的特定物理信息,比如電子密度、電場強度和電子溫度等.可以說,隨著放電參數的輸入,DNN 幾乎可以實時地輸出放電特征量.而流體模擬和粒子模擬分別需要大約半個小時和幾十個小時才能獲得一組穩定的模擬結果.在與傳統的數值模擬相同的計算精度下(相對誤差小于0.5%),經過訓練后DNN 的預測效率較傳統數值模擬方法的計算效率提高了約105～ 107倍,當然這里并不包括訓練DNN 所需的時間.這意味數據驅動的計算模型可以近乎實時地給出低溫等離子體的物理信息,這對于在大氣壓下一些需要實時監測與調控的等離子體應用具有重要的價值,特別是與智能化相關的應用中會起到關鍵性的作用.此外,經過訓練后的DNN 可以迅速地獲得給定范圍內任一放電參數下的大氣壓射頻放電特性,這意味著DNN 能夠在有限的訓練數據的基礎上,給出大量的計算數據,從而可以極大地強化數值模擬效果.比如圖7 給出的伏安特性曲面與圖13 給出的EEDF 曲面.

簡單地說,以流體模擬與粒子模擬為代表的傳統低溫等離子體物理模擬方法雖然受限于計算效率,但是可以一次性給出放電等離子體的全部物理信息,甚至如粒子模擬可以精確地給出放電等離子體的動理學特性,是揭示等離子體物理特性的根本方法.以DNN 為代表的數據驅動方法,雖然可以大幅提高計算效率,乃至可以做到“實時”給出放電等離子體的物理信息,但是一般只能給出特定的單一物理信息,比如對于預測電子密度的DNN,由于只通過訓練獲得了電子密度數據信息,也就只能預測電子密度的信息,而對電場強度、電子溫度等信息則需要訓練其他DNN 給出.

從另一個角度來看,本文討論的DNN 數據驅動模型,雖然有極高的計算效率,能夠給出海量的反映等離子體性質的計算數據,但是訓練數據本身來源于粒子模型或流體模型,這意味著DNN 給出的數據信息一般不會超出現有粒子模型與流體模型所能給出的物理現象,即現有的DNN 模型可能不具備發現新物理規律的能力.然而,隨著人工智能技術的進一步發展,新的神經網絡技術,比如PINNs[36],DeepONet[37],FNO[38]等將有可能進一步提升與優化現有的粒子模型與流體模型的實現方式,比如借助于神經網絡逼近而不是傳統的離散化方法來實現粒子模擬與流體模擬,這可能會極大地提高計算效率,并平滑推進高維模擬,大幅優化模擬結果,進而推動發現新的等離子體物理規律.

可以說,以DNN 為代表的數據驅動技術為低溫等離子體的計算帶來了一種全新的且極具發展前景的工具.可以預見,在未來的研究中,粒子模型與流體模型將繼續在揭示等離子體物理性質方面發揮重要作用,先進的數據驅動技術也會有效彌補現有流體模型和粒子模型在數值實現方式上的不足,為發現新的等離子體物理規律提供可能.另一方面,在許多需要實時檢測與反饋的等離子體應用中,尤其是以智能化為特色的放電等離子體應用中,數據驅動技術將成為不可或缺的工具.

本研究中的Python 程序及訓練數據集已開源:https://github.com/SDU-HV-Plasma/DNN2RF.git.