求解帶有混合約束的極大極小優化問題的神經網絡方法

沈 潔, 解昱菲, 鄭欣蕾

(遼寧師范大學 數學學院,遼寧 大連 116081)

極大極小優化問題在電路設計、管理科學及經濟學等許多領域有廣泛應用. 由于極大極小優化問題的目標函數不可微,因此有兩個解決問題的方向,一種是用非光滑函數的次梯度生成目標函數的割平面近似模型,這種方法雖然模型清晰,但在計算次梯度時,往往會遇到較大困難. 另一種方法是通過引入變量將極大極小優化問題進行光滑化處理,再利用經典的優化方法,如線搜索算法、信賴域算法和罰函數法等進行求解,如文獻[1]中借助半罰函數思想,提出了一個廣義投影算法,該算法的特點是,由一個廣義梯度投影顯式公式產生的搜索方向是下降可行的,并構造了一個最優識別控制函數. 但這種算法在計算時間上極度依賴問題的維數、結構和算法的復雜度,因此求解高維或結構復雜的優化問題需要更好的方法. 本文通過構建神經網絡求解極大極小非光滑優化問題, 首先利用最大熵函數近似非光滑的目標函數,將問題轉化為光滑優化問題,再構建用常微分方程刻畫的動態系統(遞歸神經網絡). 理論分析證明了動態系統的解軌線收斂到優化問題的近似最優解. 最后給出的數值實驗證明了所構造遞歸神經網絡求極大極小問題的有效性.

1 預備知識

考慮下述極大極小問題:

(1)

其中,x∈n,X={x∈n|l≤x≤h},l=(l1,l2,…,ln)T,h=(h1,h2,…,hn)T.fi(x),gk(x)是二次連續可微凸函數,A∈r×n,rank(A)=r,b∈r.記Ξ={x∈n|gk(x)≤0,k=1,2,…,m,Ax=b,x∈X},盡管fi(x)(i=1,2,…,s)都是連續可微函數,但是目標函數是非光滑函數.

假設1(i)問題(1)的最優解存在;

下面給出如下最大熵函數[1]:

(2)

最大熵函數fp(x)是一個光滑函數,它具有如下良好的性質.

引理1[2](i)隨著p趨于無窮,fp(x)逐點收斂到f(x).

(ii)隨著p趨于無窮,fp(x)一致收斂到f(x).

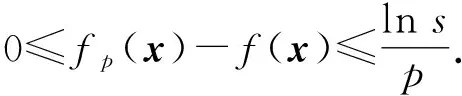
(iv)如果每個fi(x)(i=1,2,…,s)在凸集Ξ上都是凸函數,那么fp(x)也是凸函數.

根據上面熵函數的性質,可以將原問題(1)近似為下面的光滑凸優化問題:

(3)

其中,g(x)=(g1(x),g2(x),…,gm(x))T,fp(x),gk(x)(k=1,2,…,m)都是二次連續可微凸函數.

光滑熵函數fp(x)能夠很好地近似原問題(1)中的非光滑函數f(x),因此光滑凸優化問題(3)的最優解是原問題(1)的近似最優解,而且p越大,近似效果越好. 所以只需求解近似問題(3)就能得到原問題的近似最優解.根據最優性條件[3],知道,x*是問題(3)的最優解當且僅當對任意的x∈Ξ,有(x-x*)T?fp(x)≥0,其中,?fp(x)表示fp(x)的梯度.

定理1[4]設Ω?n是非空閉凸集,x*∈Ω,F:Ω→n為連續映射,則x*滿足變分不等式(x-x*)TF(x*)≥0,?x∈Ω的充要條件是x*滿足投影方程-x*+PΩ(x*-F(x*))=0.

2 投影神經網絡模型構建

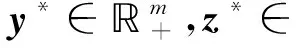
其中,?g(x)=(?g1(x),?g2(x),…,?gm(x))T表示g(x)的Jacobian矩陣.

為了求解近似問題(3),構建如下遞歸神經網絡模型:

(4)

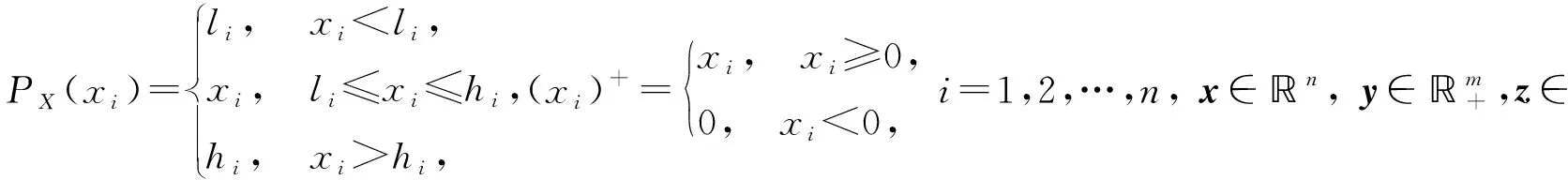
3 穩定性與收斂性分析

這里主要采用文獻[6-7]中的方法討論神經網絡(4)的穩定性和收斂性.

引理2(i)神經網絡(4)至少存在一個平衡點.如果(x*,y*,z*)是神經網絡(4)的平衡點,那么x*是問題(3)的最優解.

(ii)對任意初始點,神經網絡(4)存在唯一的連續解.

(iii)設u(t)=(x(t),y(t),z(t))是神經網絡(4)的帶有初值u(t0)=(x(t0),y(t0),z(t0))的解軌線,如果x(t0)∈X且y(t0)≥0,那么有x(t)∈X和y(t)≥0.下面具體分析構建的神經網絡(4)的穩定性和收斂性.

定理2假設?2fp(x)在Ξ上是正定矩陣,那么帶有初值u(t0)=(x(t0),y(t0),z(t0))的神經網絡(4)在Lyapunov意義下是穩定的,而且x(t)指數收斂到問題(3)的最優解x*.

考慮下面的Lyapunov函數:

其中,u*=(x*,y*,z*)是神經網絡(4)的平衡點,且

又因為投影不等式[6]:

(v-PΩ(v))T(PΩ(v)-u)≥0,?v∈n+m+r,u∈Ω,

-G(u)T{PΩ(u-G(u))-u}≥‖PΩ(u-G(u))-u‖2.

注意到T(u)=PΩ(u-G(u))-u,則

O1∈n×m,O2∈n×r,O3∈r×m,O4∈r×r是零矩陣. 注意到yi≥0,?2gi(x)是半正定的,那么?G(u)也是半正定的,且T(u)T?G(u)T(u)≥0,因此得到

G(u)T(u-u*)≥(G(u)-G(u*))T(u-u*),

因此

一方面,有

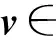
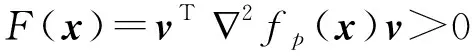
由于問題(3)是極大極小問題(1)的近似問題,因此神經網絡(4)指數收斂到極大極小問題(1)的近似最優解.

4 數值實驗

考慮如下極大極小優化問題:

該問題最優解為x*=(1.1390,0.8996)T. 令

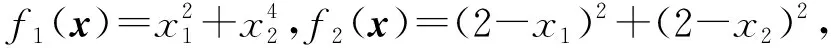
數值結果表明神經網絡(4)的解軌線收斂到其平衡點x*=(1.1378,0.8998)T. 圖1顯示了帶有6個不同初始點的基于神經網絡(4)的解軌線x(t),從圖中可以看出6條解軌線均收斂到近似問題的平衡點,也就是原問題的近似解(1.1378,0.8998)T. 該數值實驗表明,應用本文提出的遞歸神經網絡可以得到極大極小優化問題的近似最優解.

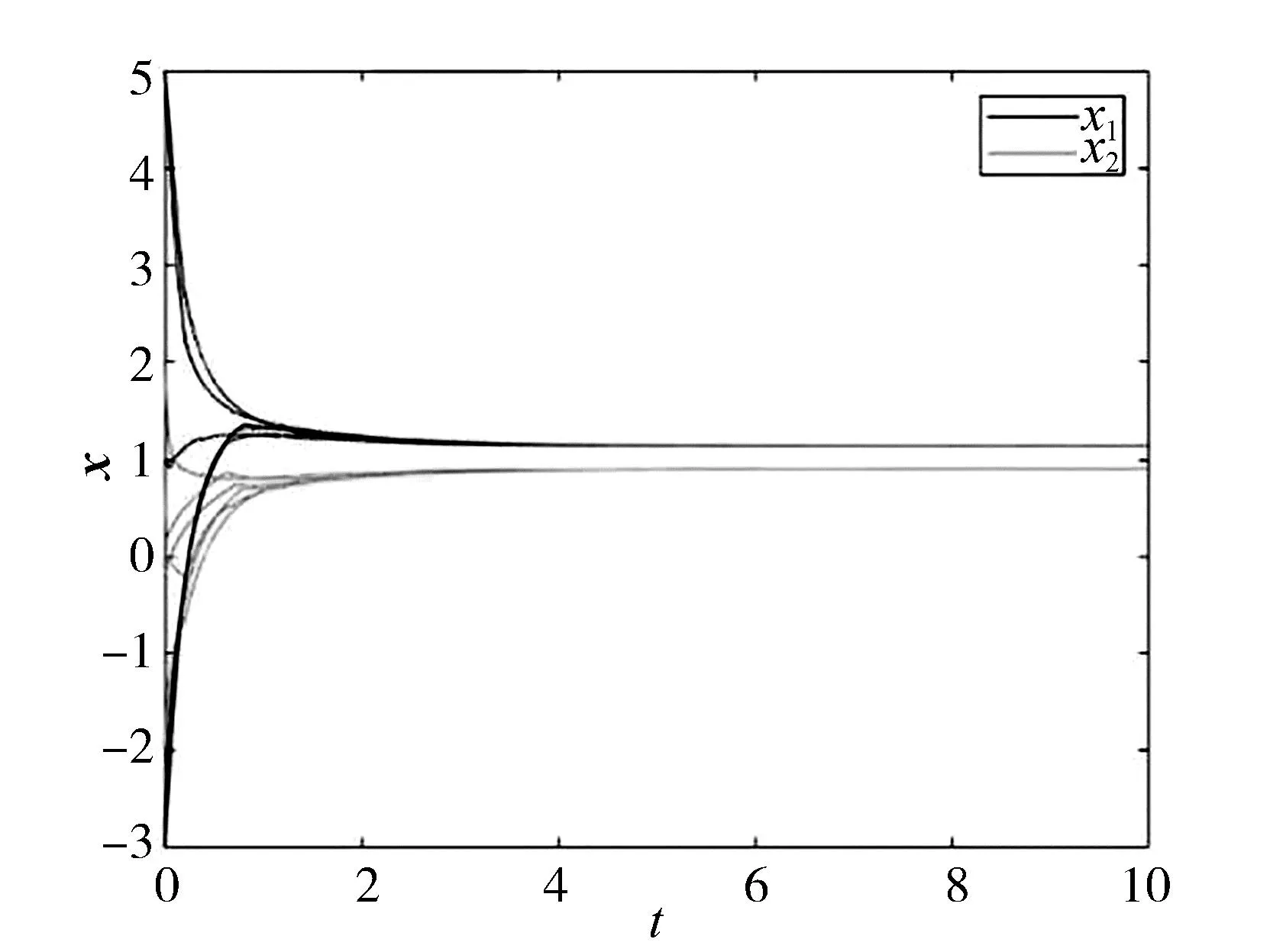
圖1 神經網絡的解軌線Fig.1 The trajectories of neural network