粒子加速器準(zhǔn)直中測(cè)站坐標(biāo)系高精度恢復(fù)方法

陳 哲,范百興,鄒方星,段童虎,黃 赫

(信息工程大學(xué) 地理空間信息學(xué)院,河南 鄭州 450001)

粒子加速器作為“大國(guó)重器”,為物理、醫(yī)學(xué)、材料科學(xué)等眾多學(xué)科提供大量尖端研究手段[1]。為保證粒子按照設(shè)計(jì)軌道運(yùn)行,對(duì)準(zhǔn)直測(cè)量精度提出了很高要求[2]。準(zhǔn)直測(cè)量工作的主要任務(wù)是將所有元件高精度安裝至設(shè)計(jì)位置,實(shí)際測(cè)量過(guò)程中,需要在實(shí)驗(yàn)室進(jìn)行元件預(yù)準(zhǔn)直,即將多個(gè)元件安裝在同一支架上,作為一個(gè)預(yù)準(zhǔn)直單元,之后運(yùn)輸至粒子加速器隧道進(jìn)行現(xiàn)場(chǎng)安裝[3]。為提高測(cè)量效率、保證測(cè)量精度,中國(guó)散裂中子源[4]基于最小二乘原理,恢復(fù)激光跟蹤儀測(cè)站坐標(biāo)系,并設(shè)計(jì)制作專用吊車完成預(yù)準(zhǔn)直單元安裝;北京高能同步輻射光源[5]利用振動(dòng)線完成磁鐵磁中心引出,保證誤差在10 μm內(nèi)的情況下,基于多路激光“三高一低”的布設(shè)方案進(jìn)行預(yù)準(zhǔn)直[6],這與北京正負(fù)電子對(duì)撞機(jī)[7]均基于坐標(biāo)轉(zhuǎn)換原理,先恢復(fù)激光跟蹤儀測(cè)站坐標(biāo)系,再進(jìn)行預(yù)準(zhǔn)直單元安裝。國(guó)內(nèi)粒子加速器隧道控制網(wǎng)主要采用激光跟蹤儀多測(cè)站架設(shè)建立三維控制網(wǎng)[2],由于高程方向誤差累積明顯,王小龍等[8]將大地水準(zhǔn)面作為基準(zhǔn)獲取高程數(shù)據(jù),建立附有高程約束的三維平差,實(shí)現(xiàn)高程方向誤差累積的有效控制。

目前有關(guān)粒子加速器準(zhǔn)直測(cè)量工作的研究,主要集中在元件預(yù)準(zhǔn)直及高精度控制網(wǎng)的布設(shè)。針對(duì)測(cè)站坐標(biāo)系的恢復(fù)問(wèn)題,往往基于公共點(diǎn)坐標(biāo)轉(zhuǎn)換算法,依據(jù)最小二乘原理實(shí)現(xiàn)[3],并未顧及控制點(diǎn)在全局及激光跟蹤儀測(cè)站坐標(biāo)系下的點(diǎn)位誤差。現(xiàn)有較為成熟且廣泛應(yīng)用的坐標(biāo)轉(zhuǎn)換方法主要有奇異值分解(singular value decomposition,SVD)法[9]、四元數(shù)法[10]、正交Procrustes法[11]、羅德里格矩陣法[12]、加權(quán)整體最小二乘(weighted total least squares,WTLS)法[13]等,均根據(jù)公共點(diǎn)坐標(biāo)距離平方和最小構(gòu)造目標(biāo)函數(shù),基于最小二乘算法獲取最優(yōu)解。其中,SVD法與正交Procrustes法理論簡(jiǎn)單易實(shí)現(xiàn),但當(dāng)公共點(diǎn)過(guò)于密集時(shí),旋轉(zhuǎn)矩陣的正確性無(wú)法保證;四元數(shù)法基于線性微分方程,獲取旋轉(zhuǎn)矩陣,運(yùn)算簡(jiǎn)單,且在求解過(guò)程中,不存在奇異點(diǎn);羅德里格矩陣法穩(wěn)定性強(qiáng),但計(jì)算過(guò)程復(fù)雜,不易實(shí)現(xiàn)。文獻(xiàn)[14]研究表明,上述方法在進(jìn)行坐標(biāo)轉(zhuǎn)換過(guò)程中,精度差值均在2 μm內(nèi),相差較小,但均未考慮點(diǎn)位誤差對(duì)轉(zhuǎn)化精度的影響。WTLS法顧及觀測(cè)值及系數(shù)矩陣的隨機(jī)誤差,同時(shí)考慮到系數(shù)矩陣中各隨機(jī)元素的精度不同,在一定程度上提高了轉(zhuǎn)換精度,但無(wú)法顧及旋轉(zhuǎn)矩陣正交約束條件。針對(duì)此問(wèn)題,本研究構(gòu)建了顧及點(diǎn)位統(tǒng)計(jì)性質(zhì)的測(cè)站坐標(biāo)系恢復(fù)模型,在考慮旋轉(zhuǎn)矩陣正交約束條件的基礎(chǔ)上,利用李代數(shù)思想對(duì)已構(gòu)建的數(shù)學(xué)模型進(jìn)行線性化和迭代計(jì)算,并通過(guò)仿真與實(shí)測(cè)實(shí)驗(yàn),驗(yàn)證了本研究方法的正確性及有效性,相較于傳統(tǒng)測(cè)站坐標(biāo)系恢復(fù)方法精度更高。

1 測(cè)站坐標(biāo)恢復(fù)

1.1 測(cè)站坐標(biāo)恢復(fù)及元件安裝原理

粒子加速器設(shè)計(jì)過(guò)程中,需確定設(shè)備基準(zhǔn)點(diǎn)在待安裝全局坐標(biāo)系中的理論坐標(biāo)值。目前,全局坐標(biāo)系作為準(zhǔn)直測(cè)量的全局基準(zhǔn),主要利用GNSS、陀螺全站儀、水準(zhǔn)儀等進(jìn)行觀測(cè),通過(guò)布設(shè)一級(jí)地面網(wǎng)提供絕對(duì)位置參考,因控制網(wǎng)的精度逐層增高,只保留必要起算數(shù)據(jù)控制二級(jí)隧道網(wǎng)[15];利用激光跟蹤儀、水準(zhǔn)儀等構(gòu)建附加約束的三維控制網(wǎng),提供高精度相對(duì)定位[16]。隧道網(wǎng)控制點(diǎn)分布在隧道內(nèi)截面方向的墻面、地面和頂面,如圖1所示。

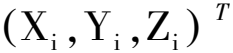
(1)

εi=Xi-k(Rxi+T)。

(2)

其中:R、T分別為控制點(diǎn)在兩坐標(biāo)系下的3×3旋轉(zhuǎn)矩陣、3×1平移矩陣;εi為3×1的測(cè)站坐標(biāo)系恢復(fù)殘差矩陣,考慮到激光跟蹤儀的高精度測(cè)距能力,取k=1。

預(yù)準(zhǔn)直時(shí),采用水準(zhǔn)儀、經(jīng)緯儀、激光跟蹤儀、電子水平儀、振動(dòng)線技術(shù)等,確定元件機(jī)械重心與物理重心的關(guān)系,并關(guān)聯(lián)至元件基準(zhǔn)點(diǎn)上[17]。此時(shí),利用激光跟蹤儀測(cè)量待安裝元件基準(zhǔn)點(diǎn)yi,按照式(3),基于已恢復(fù)的測(cè)站坐標(biāo)系,將元件基準(zhǔn)點(diǎn)坐標(biāo)轉(zhuǎn)換至全局坐標(biāo)系下,計(jì)算設(shè)計(jì)位置的偏差并進(jìn)行準(zhǔn)直調(diào)整。

Yi=Ryi+T。

(3)

其中:Yi、yi分別為待安裝元件的基準(zhǔn)點(diǎn)在全局與激光跟蹤儀測(cè)站坐標(biāo)系下三維坐標(biāo)。

1.2 構(gòu)建數(shù)學(xué)模型

粒子加速器二級(jí)隧道控制網(wǎng)通過(guò)多測(cè)站聯(lián)合平差解算(Xi,Yi,Zi),(xi,yi,zi)依據(jù)激光跟蹤儀球坐標(biāo)測(cè)量原理獲取,如圖2所示。

圖2 多測(cè)站聯(lián)合測(cè)量及球坐標(biāo)測(cè)量原理

(4)

其中:Si、Vi、Hi分別為距離、天頂距、水平角觀測(cè)值。對(duì)式(4)取全微分,得到系數(shù)矩陣K。按照方差-協(xié)方差傳播定律計(jì)算方差-協(xié)方差矩陣

(5)

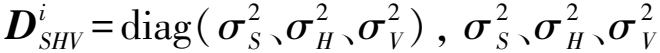
顧及控制點(diǎn)在全局坐標(biāo)系和測(cè)站坐標(biāo)系下點(diǎn)位誤差對(duì)式(1)中R、T計(jì)算結(jié)果準(zhǔn)確度的影響,根據(jù)方差-協(xié)方差傳播定律確定權(quán)陣

(6)

擴(kuò)展式(2)為:

(7)

此時(shí),式(7)中涉及的極小值問(wèn)題可以轉(zhuǎn)化為:

(8)

構(gòu)建數(shù)學(xué)模型,則求解問(wèn)題可以轉(zhuǎn)化為解算方程:

wi(Xi-Rxi-T)=0。

(9)

1.3 線性化方法

非線性方程組的求解分為最優(yōu)化迭代和智能優(yōu)化方法,其中最優(yōu)化迭代計(jì)算依賴初值的選取,且易陷入局部最優(yōu);智能優(yōu)算法面臨求解精度不高,且針對(duì)特定問(wèn)題無(wú)法保障解算性能等問(wèn)題。相對(duì)于非線性方程,線性方程的求解技術(shù)更加成熟[18],目前主要依據(jù)最小二乘算法實(shí)現(xiàn)。針對(duì)坐標(biāo)轉(zhuǎn)換問(wèn)題,擴(kuò)展至加權(quán)整體最小二乘算法,但該算法推導(dǎo)繁瑣、不便于理解,坐標(biāo)轉(zhuǎn)換精度影響因素不直觀,且無(wú)法顧及旋轉(zhuǎn)矩陣正交約束條件。因此提出李代數(shù)理論,李群(SO(3))是具有群結(jié)構(gòu)的光滑流形,李代數(shù)是其單位元處的正切空間,旋轉(zhuǎn)矩陣屬于SO(3)[19]。根據(jù)李代數(shù)理論,將目標(biāo)函數(shù)線性化,之后進(jìn)行迭代計(jì)算,獲取未知參數(shù)高精度解算結(jié)果。

旋轉(zhuǎn)矩陣R通過(guò)李代數(shù)指數(shù)映射和冪級(jí)數(shù)展開(kāi)獲得:

(10)

此時(shí)式(9)可表示為:

(11)

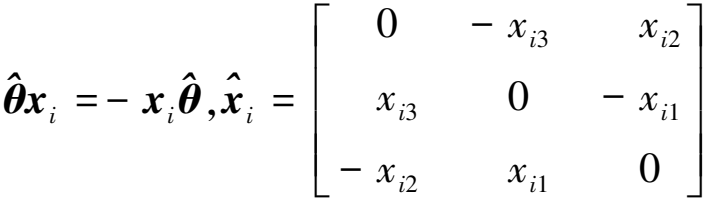
(12)

此時(shí),式(11)可表示為:

(13)

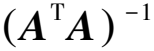
1.4 迭代算法

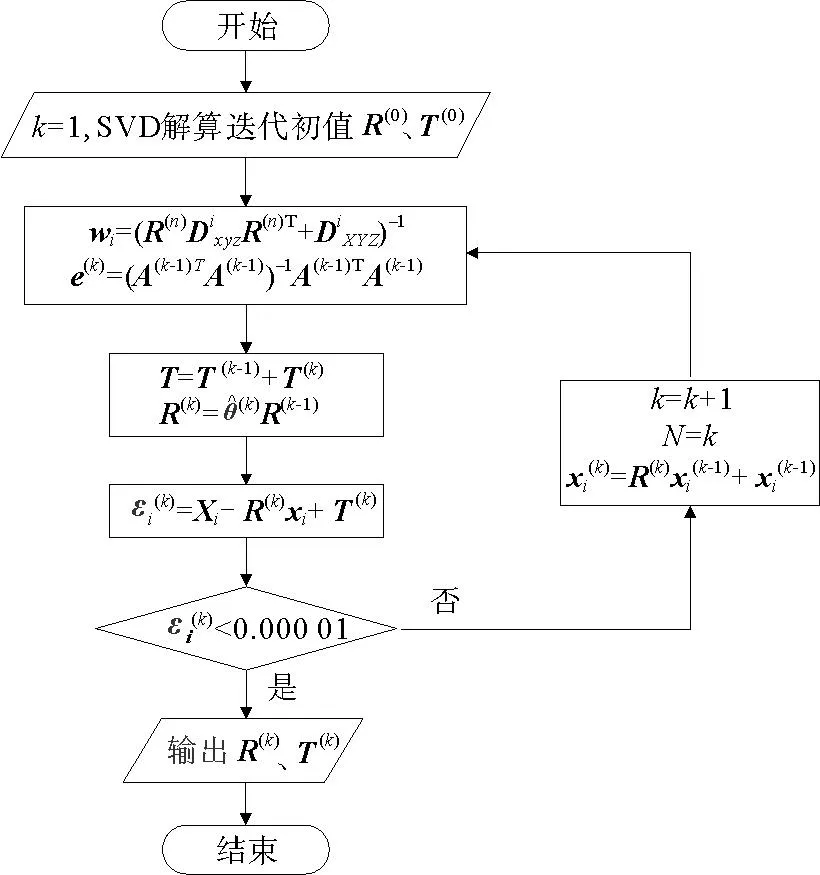
圖3 計(jì)算流程圖

(14)

2 誤差分析

(15)

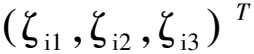
(16)

將式(16)代入式(15)得:

(17)

根據(jù)式(10)和簡(jiǎn)化式(17)可得:

(18)

式(11)可變換為下列方程組:

(19)

wiCW=wie,

(20)

由此可得,解算結(jié)果誤差由控制網(wǎng)點(diǎn)平差解算算法、觀測(cè)誤差、測(cè)站坐標(biāo)系下觀測(cè)誤差及控制點(diǎn)布局決定。測(cè)站坐標(biāo)系恢復(fù)過(guò)程中,控制點(diǎn)在全局和測(cè)站坐標(biāo)系下三維坐標(biāo)精度、空間布局、數(shù)目等因素均影響解算結(jié)果。

3 仿真分析

分別利用WTLS方法和本研究方法進(jìn)行數(shù)據(jù)處理。對(duì)比兩種方法解算所得的旋轉(zhuǎn)矩陣、平移矩陣元素及與其真值的差值,結(jié)果如圖4所示。相較于WTLS算法,本研究提出的線性迭代解法所得的旋轉(zhuǎn)、平移矩陣精度明顯提高,其中旋轉(zhuǎn)矩陣元素最多提高2 μm,平均提高1 μm;平移矩陣最大提高4.9 μm,平均提高1 μm。通過(guò)改變公共點(diǎn)個(gè)數(shù)計(jì)算兩種方法對(duì)應(yīng)的均方根誤差(root mean square error,RMSE),如表1所示。

表1 不同公共點(diǎn)按照WTLS和本研究方法的RMSE

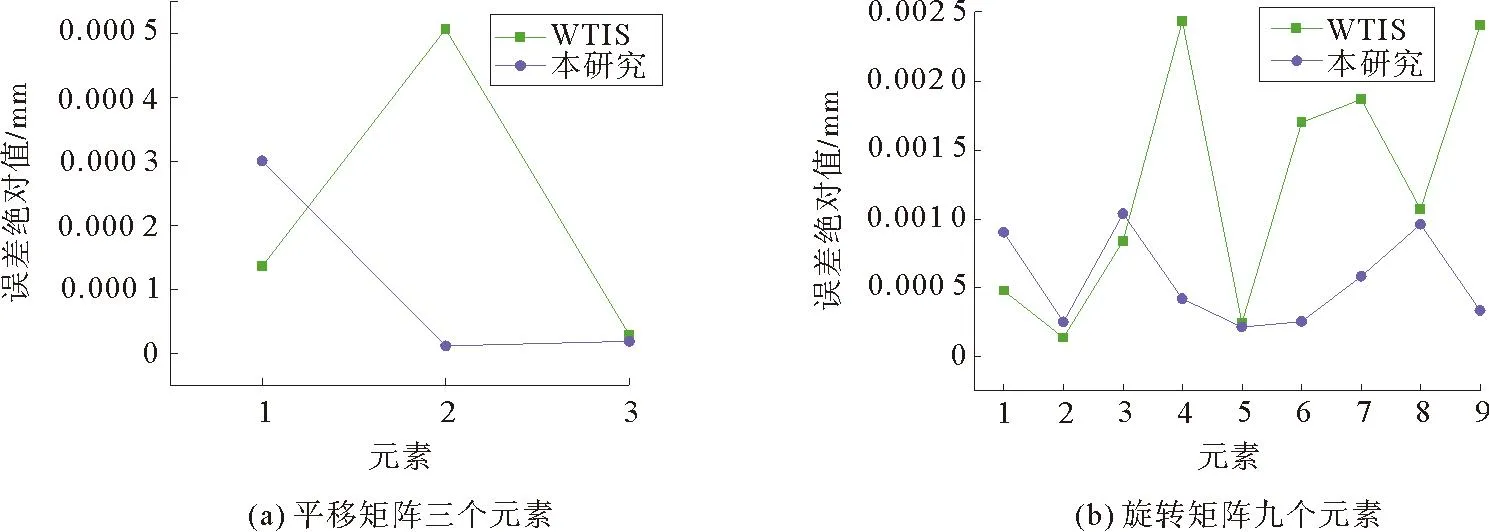
圖4 不同方法解算的旋轉(zhuǎn)、平移矩陣元素及與其真值的差值

由表1中可知,相較于WTLS算法,本研究方法在進(jìn)行測(cè)站坐標(biāo)系恢復(fù)時(shí),RMSE明顯降低,最少降低4 μm,最多降低42 μm,在3～8個(gè)公共點(diǎn)的情況下平均降低18 μm。仿真結(jié)果驗(yàn)證了本研究方法的正確性。

4 實(shí)測(cè)驗(yàn)證

在溫度相對(duì)穩(wěn)定的某光源直線段內(nèi)利用AT960激光跟蹤儀進(jìn)行多測(cè)站觀測(cè),保證相鄰測(cè)站至少存在3個(gè)公共點(diǎn)。如圖5所示,實(shí)驗(yàn)前儀器經(jīng)過(guò)計(jì)量檢定符合標(biāo)稱精度。

圖5 測(cè)站及控制點(diǎn)分布

以第一測(cè)站坐標(biāo)系為全局坐標(biāo)系,按照多測(cè)站聯(lián)合平差方式獲取控制點(diǎn)全局坐標(biāo)[22]。在直線段某磁鐵附近,自由設(shè)站架設(shè)激光跟蹤儀,對(duì)已知全局坐標(biāo)的控制點(diǎn)進(jìn)行觀測(cè),得到25個(gè)全局控制點(diǎn)在測(cè)站坐標(biāo)系下的三維坐標(biāo)。張皓琳等[23]研究表明,在進(jìn)行坐標(biāo)轉(zhuǎn)換過(guò)程中,隨公共點(diǎn)個(gè)數(shù)增加,轉(zhuǎn)換誤差減小,但當(dāng)公共點(diǎn)超過(guò)6個(gè)時(shí),轉(zhuǎn)換精度改善不明顯。為兼顧測(cè)量精度和實(shí)際測(cè)量過(guò)程中測(cè)站坐標(biāo)系恢復(fù)效率,選擇8個(gè)公共點(diǎn)進(jìn)行測(cè)站坐標(biāo)系恢復(fù),8個(gè)公共點(diǎn)在全局及測(cè)站坐標(biāo)系的三維坐標(biāo)如表2所示。

表2 8個(gè)公共點(diǎn)在全局及測(cè)站坐標(biāo)系的三維坐標(biāo)

分別利用WTLS方法和本研究方法對(duì)兩組坐標(biāo)進(jìn)行處理,恢復(fù)自由設(shè)站激光跟蹤儀測(cè)站坐標(biāo)系,得到兩種方法的RMSE,如圖6所示。相較于WTLS算法,本研究方法在進(jìn)行測(cè)站坐標(biāo)系恢復(fù)時(shí),RMSE明顯降低,其中最少降低27 μm,最多降低36 μm,在3～8個(gè)公共點(diǎn)的情況下平均降低30 μm,減小了54.5%,驗(yàn)證了本研究方法與傳統(tǒng)方法相比恢復(fù)精度明顯提高。當(dāng)公共點(diǎn)大于6時(shí),解算精度趨于穩(wěn)定,與文獻(xiàn)[23]結(jié)論一致。將測(cè)站坐標(biāo)系除公共點(diǎn)外17個(gè)控制點(diǎn)的三維坐標(biāo),分別利用WTLS與本研究方法恢復(fù)的測(cè)站坐標(biāo)系參數(shù)轉(zhuǎn)換至全局坐標(biāo)下,計(jì)算坐標(biāo)分量與全局坐標(biāo)系下三維坐標(biāo)分量之差,結(jié)果如圖7所示。

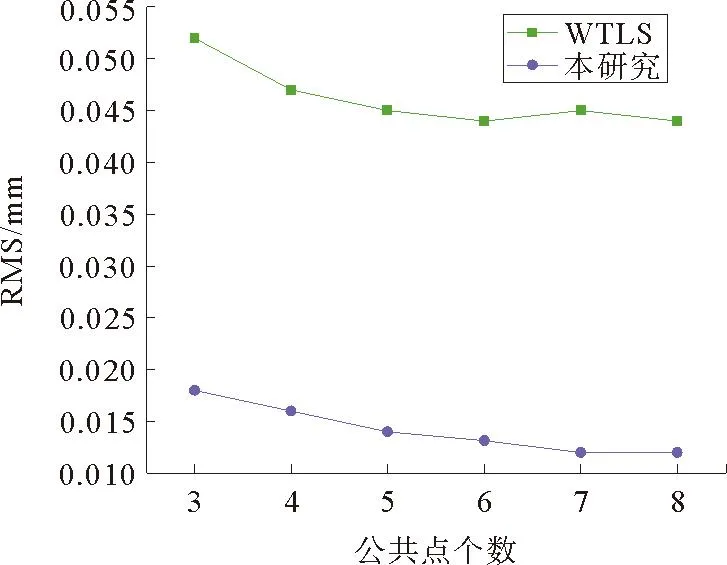
圖6 不同公共點(diǎn)按照WTLS和本研究方法解算所得RMSE

圖7 兩種方法轉(zhuǎn)換后三維坐標(biāo)分量與全局坐標(biāo)分量之差

由圖7可知,利用WTLS方法恢復(fù)測(cè)站坐標(biāo)系,將非公共點(diǎn)三維坐標(biāo)轉(zhuǎn)換至全局坐標(biāo),轉(zhuǎn)換后各點(diǎn)坐標(biāo)分量與全局坐標(biāo)同一點(diǎn)坐標(biāo)分量的差值最大為22 μm,最小為2 μm,平均為8 μm。根據(jù)本研究方法恢復(fù)測(cè)站坐標(biāo)系,非公共點(diǎn)轉(zhuǎn)換后各點(diǎn)坐標(biāo)分量與全局坐標(biāo)同一點(diǎn)坐標(biāo)分量差值最大為12 μm,最小為0.5 μm,平均為5 μm。實(shí)測(cè)結(jié)果表明,依據(jù)本研究方法進(jìn)行測(cè)站坐標(biāo)系恢復(fù),顧及點(diǎn)位位于測(cè)站及全局坐標(biāo)系下點(diǎn)位誤差的同時(shí),還考慮旋轉(zhuǎn)矩陣的正交約束條件,比WTLS方法恢復(fù)的測(cè)站坐標(biāo)系精度更高。

仿真分析和實(shí)測(cè)實(shí)驗(yàn)驗(yàn)證了本研究提出的線性迭代算法恢復(fù)測(cè)站坐標(biāo)系的正確性,同時(shí)依據(jù)激光跟蹤儀測(cè)站坐標(biāo)系恢復(fù)的RMSE,以及基于已恢復(fù)的測(cè)站坐標(biāo)系參數(shù),將測(cè)站坐標(biāo)系三維坐標(biāo)轉(zhuǎn)換至全局坐標(biāo)系,得到與全局坐標(biāo)系三維坐標(biāo)分量的差值。結(jié)果表明,針對(duì)測(cè)站坐標(biāo)系恢復(fù)問(wèn)題,考慮點(diǎn)位在測(cè)站及全局坐標(biāo)系的點(diǎn)位誤差基礎(chǔ)之上還顧及旋轉(zhuǎn)矩陣正交約束條件,引入李代數(shù)理論迭代計(jì)算恢復(fù)測(cè)站坐標(biāo)系,理論更加嚴(yán)密、恢復(fù)精度更高,對(duì)實(shí)際測(cè)量工程具有實(shí)用價(jià)值。

5 結(jié)束語(yǔ)

本研究在激光跟蹤儀測(cè)站坐標(biāo)系恢復(fù)過(guò)程中,顧及點(diǎn)位在測(cè)站及全局坐標(biāo)系下的點(diǎn)位誤差和旋轉(zhuǎn)矩陣的正交約束條件,依據(jù)李代數(shù)思想推導(dǎo)線性迭代算法,實(shí)現(xiàn)了粒子加速器準(zhǔn)直過(guò)程中激光跟蹤儀測(cè)站坐標(biāo)系高精度恢復(fù)的目的。同時(shí),定性分析了影響測(cè)站坐標(biāo)系精度恢復(fù)的因素。在此基礎(chǔ)上,分別利用本研究方法與傳統(tǒng)方法處理仿真與實(shí)測(cè)數(shù)據(jù),驗(yàn)證了本研究所提出的線性迭代算法的正確性,并在一定程度上提高了測(cè)站坐標(biāo)系恢復(fù)精度,為實(shí)現(xiàn)元件高精度安裝提供了保障。研究還發(fā)現(xiàn),測(cè)站和點(diǎn)位的布局、數(shù)目以及實(shí)測(cè)過(guò)程中大氣溫度、濕度、壓強(qiáng)、反射靶球球心偏差和入射角誤差等均影響數(shù)據(jù)的解算結(jié)果,后續(xù)可對(duì)此問(wèn)題進(jìn)一步研究。