圓錐曲線中定點和定值問題的求解策略探究
李 波
(四川省南充高級中學,四川 南充 637901)
學習《圓錐曲線與方程》章節的內容,定點和定值問題是圓錐曲線的高頻考點,該問題涉及圓錐曲線的定義、幾何性質、直線與圓錐曲線的位置關系、極坐標系和參數方程等知識,與平面向量、函數與方程、不等式等代數知識緊密聯系.
1 利用結論,快速秒殺

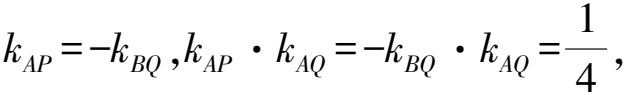
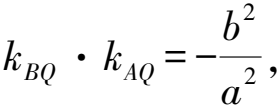
2 特值引路,先找后證
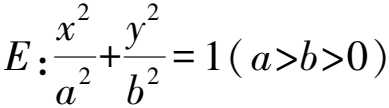
(1)求橢圓E的方程;
(2)直線MF1,NF1分別交橢圓E于C,D兩點,設直線CD與x軸交于點P,證明:|PB|為定值.
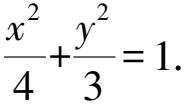
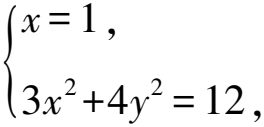


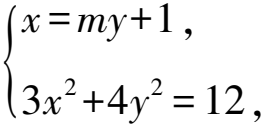
由根與系數的關系知
又F1(-1,0),所以直線MF1的方程為

由根與系數的關系知
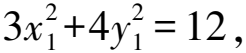


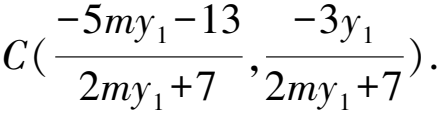
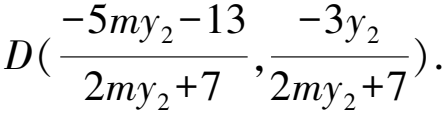
直線PC的斜率為

當直線MN的斜率為0時,不滿足M,N均在y軸的右側.
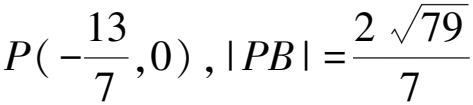
3 回歸定義,以退為進

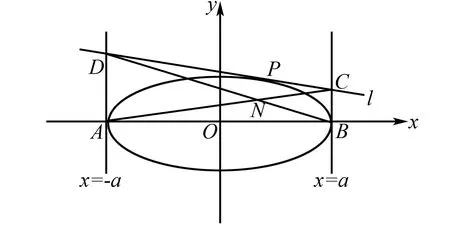
圖1 例3示意圖
(1) 求橢圓M的標準方程;
(2) 已知直線l與橢圓M相切于點P(x0,y0),且l與直線x=a和x=-a分別相交于C,D兩點,記四邊形ABCD的對角線AC,BD相交于點N.問:是否存在兩個定點F1,F2,使得|NF1|+|NF2|為定值?若存在,求出F1,F2的坐標;若不存在,說明理由.

(2)當y0=0時,由圖1知,顯然不成立.
當y0≠0時,設直線CD的方程為
y=k(x-x0)+y0,
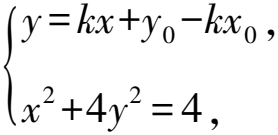
(1+4k2)x2+8k(y0-kx0)x+4(y0-kx0)2-4=0.
由直線CD與橢圓相切知△=64k2(y0-kx0)2-4(1+4k2)[4(y0-kx0)2-4]=0.
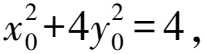
即過點P的切線方程為x0x+4yy0-4=0.







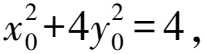
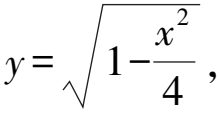
4 幾何特征,同一性轉化

(1)求C的方程;
(2)點M,N在C上,且AM⊥AN,AD⊥MN,D為垂足,證明:存在定點Q,使得|DQ|為定值.

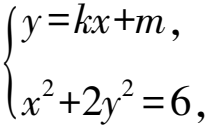
滿足△=24+48k2-8m2>0,
由根與系數的關系知

當2k+2m=m+1時,m=-2k+1,直線MN的方程為y-1=k(x-2),即直線MN過點A,不成立;


5 觀察結構,列式消元

(1)求C的方程;

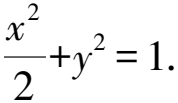
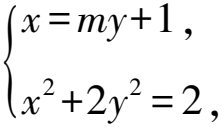
顯然△>0,由根與系數的關系知


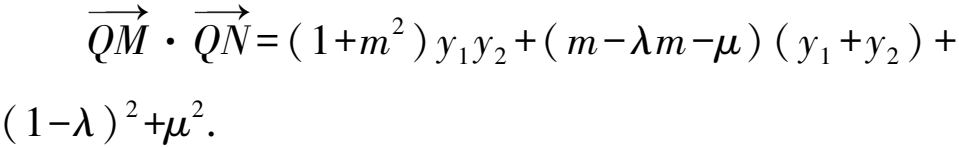

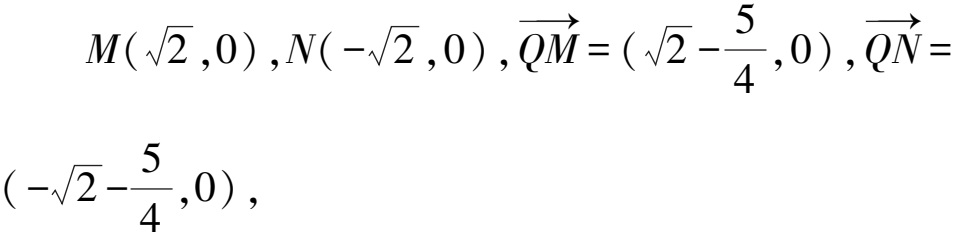
6 對偶運算,同構思想

(1)求曲線C的方程;

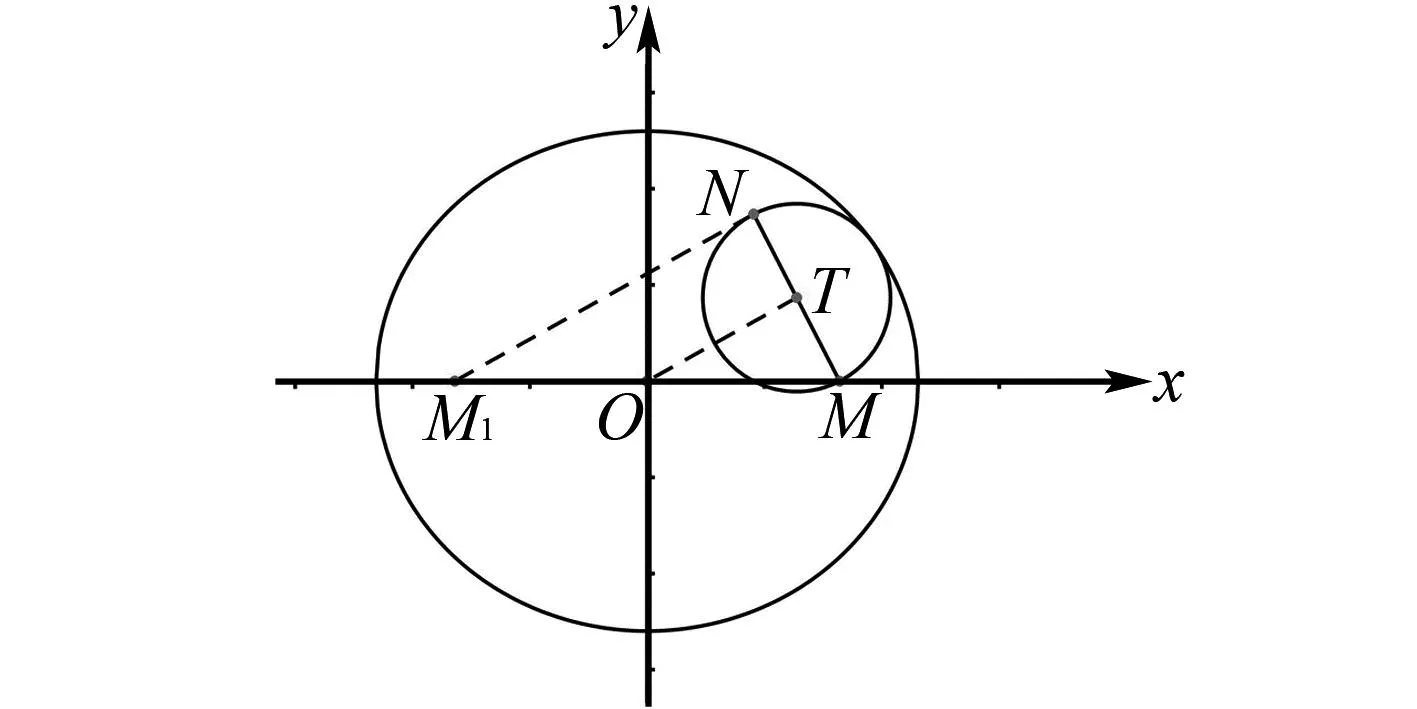
圖2 例6解析圖

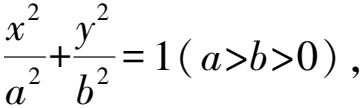
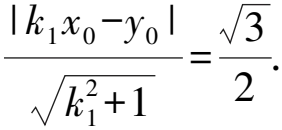

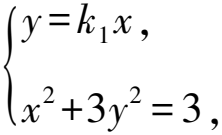
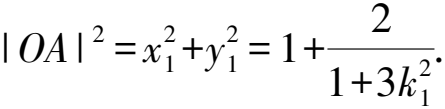



7 參數方程,有效轉化

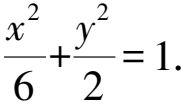
(1)求橢圓C的方程;

(2)設E(m,0),m>0,直線l的參數方程為
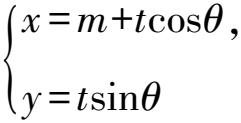

(1+2sin2θ)t2+2mtcosθ+m2-6=0,
滿足△=4m2cos2θ-4(1+2sin2θ)(m2-6)>0.
設|QA|=|t1|,|QB|=|t2|,
由根與系數的關系知

代入兩根之和、積得
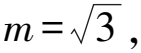

解析幾何中的定點和定值問題是圓錐曲線的高頻考點,突出了數學的學科特色,著重考查學生的理性思維和綜合運用數學思想方法發現問題、分析問題、解決問題的能力,讓學生思維的廣度與深度得到充分的展示.

