大概念下初中數學幾何章起始課的實踐與思考
——以“全等三角形章起始課”為例
沈 姍
(福建省福州第十八中學,福建 福州 350001)
大概念又稱之為大觀念,處于學科教學的核心地位,可以統籌與整合比較零散的學科知識.不僅可以明確本學科的核心知識和教學任務,還可以呈現本學科的內心概念及觀點,有機融合學科關鍵內容與思想,建構出具有系統性較強的學科框架.在初中數學幾何章起始課教學中,教師需幫助學生構建本章知識體系,引發他們的學習興趣,適當引領學生學習本章知識用到的數學方法,使其掌握本章最開始部分的知識內容,為后續學習做鋪墊[1].
1 教材內容分析
本文以人教版初中數學八年級上冊第十二章“全等三角形章起始課”教學為例,學生之前已經了解不少有關三角形的基礎知識,本節課主要學習全等三角形的概念、表示方式,以及邊角對應關系等內容.由于三角形是一個基礎性的平面幾何圖形,所以學習本課知識,既是接下來學習如何判定三角形全等和運用全等三角形的性質進行解題的基礎,也是證明線段、角相等的有效方式.故本節內容在初中數學教材中占據著相當關鍵的地位,具有承前啟后的重要作用.
2 具體教學流程
2.1 觀察圖形,引入新知
教師先在多媒體課件中出示如圖1所示的三組圖片,要求學生認真觀察,說一說每組圖片中兩個圖形之間的關系與特點,他們結合所學幾何知識與經驗,從形狀與大小兩個角度展開觀察,發現第(1)組與第(2)組中的兩個圖形不相同,通過對比自然而然得出第(3)組中兩個圖形大小、形狀完全相同,由此揭示全等圖形的概念,使其了解到可以完全重合的兩個圖形就是全等圖形.
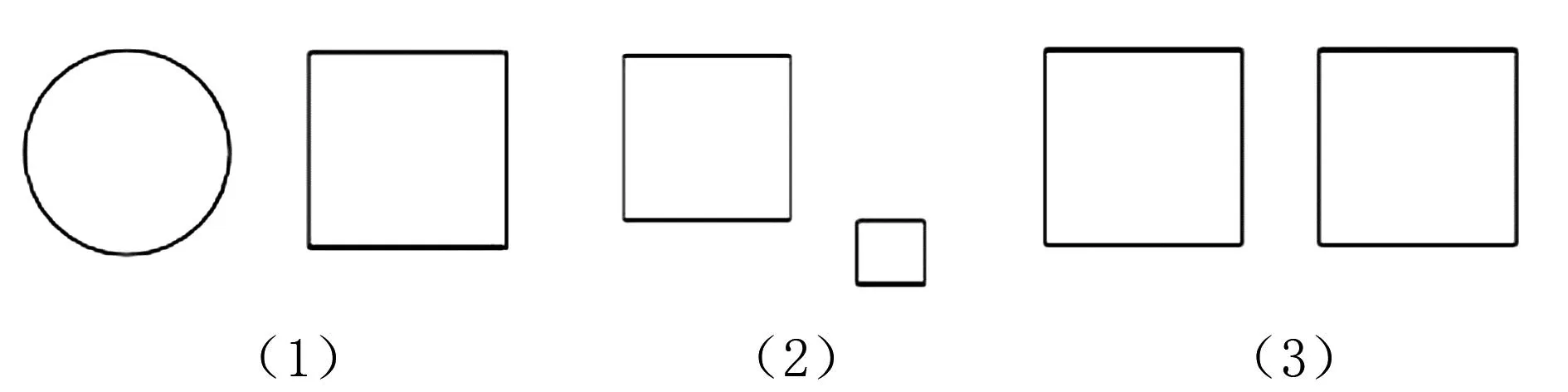
圖1 三組關系與特點不同的圖片
2.2 變化圖形,揭示概念
教師先利用信息技術手段演示三角形的三種全等變換,即為平移、翻折與旋轉,如圖2所示.引出問題:變換以后的三角形和原三角形之間有什么關系?原因是什么?大家據此能夠得到哪些結論?由學生認真觀察、思考后,指出當一個三角形經過平移、翻折或旋轉變換以后,其形狀與大小均不會發生任何變化,因而變換前后的兩個三角形是全等關系,進而發現全等三角形同位置沒有關系,只同三角形的大小與形狀有所關聯,它們能夠采用平移、翻折或旋轉的方法讓兩個三角形剛好全部重合起來.
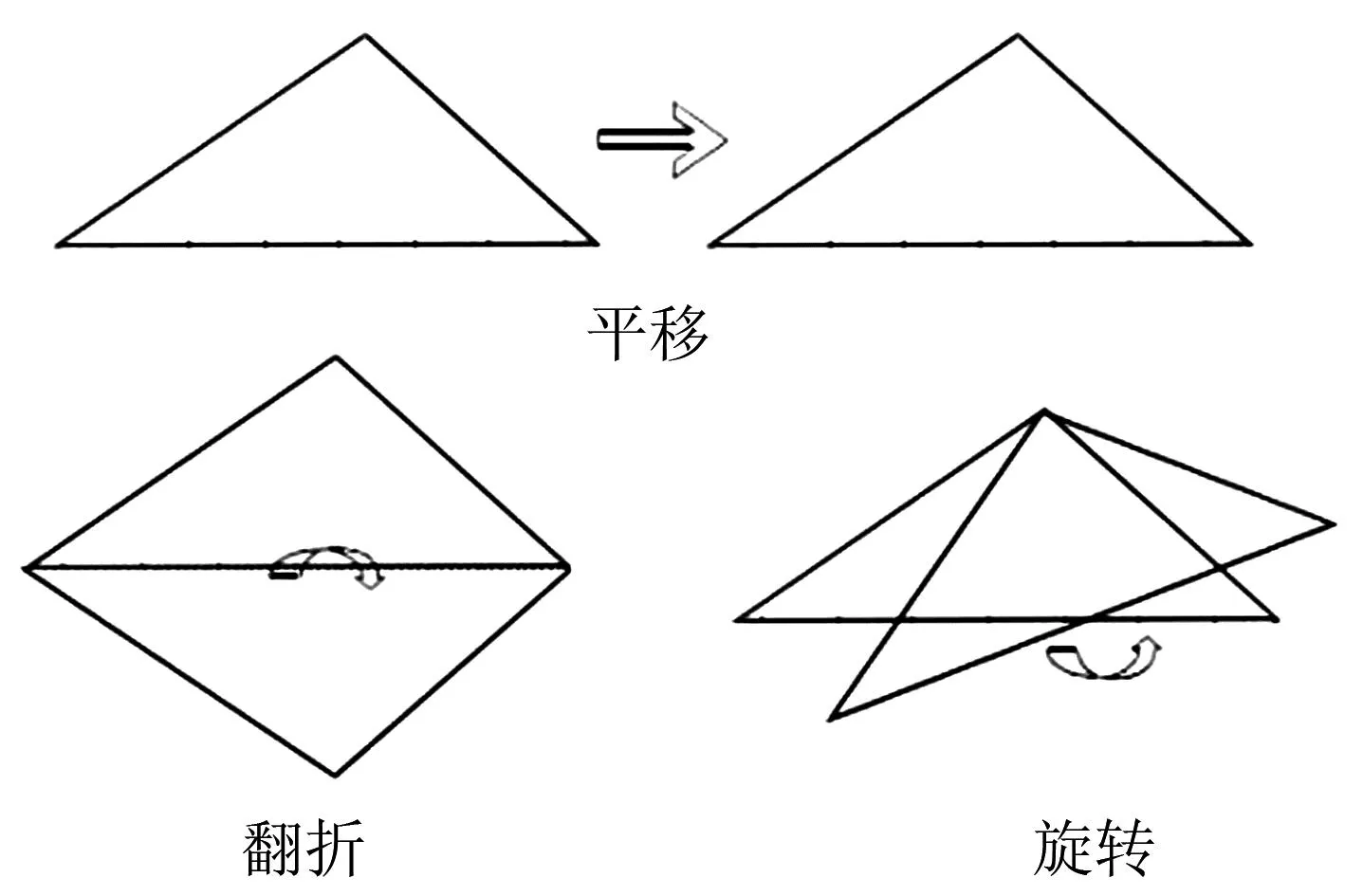
圖2 三角形的三種全等變換
接著,教師設置問題:當兩個三角形完全重合到一起以后,兩者的哪些元素也就重合起來?指導學生平移一個三角形,讓它與另一個三角形重合,觀察并指出重合的兩個三角形頂點、邊與角,使其思考與體會幾何圖形中的“對應”關系,讓他們知道重合起來的點就是對應點,相應的就是對應角與對應邊.隨后教師提問:將兩個完全一樣的三角板重合以后放在課桌上,使其中一個圍繞某頂點進行旋轉,一共有多少種不一樣的位置關系?要求學生畫出圖形且說出對應邊與對應角,繼續提問:怎么用數學符號來表示兩個三角形的全等?課件中同步出示三角形ABC與三角形DEF,如圖3所示.教師引導學生觀察重合的兩個三角形對應邊與對應角的關系,并告知他們表示方法,記作△ABC≌△DEF,讀作:三角形ABC全等于三角形DEF,應注意對應頂點要寫在對應的位置上面.在這一環節,教師通過演示課件幫助學生建立“對應”的概念,使其學會掌握全等三角形的表達方式,包括寫法和讀法,會使用全等符號,借此培養他們把文字語言轉變為數學符號語言的能力.
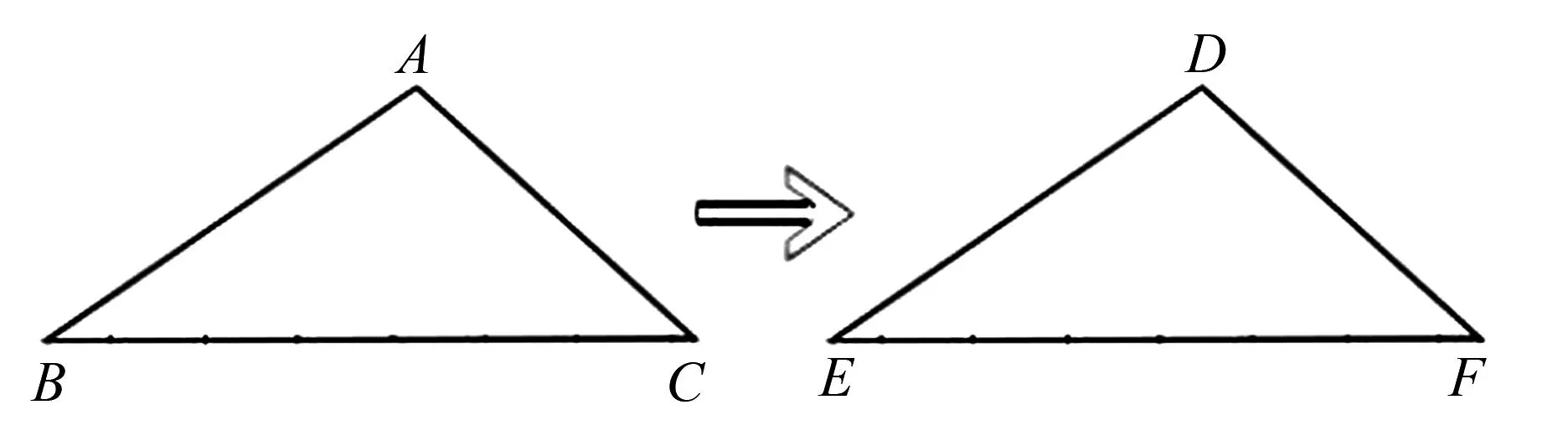
圖3 重合兩個三角形對應邊與對應角的關系
之后,教師給出問題:全等三角形的對應邊、對應角存在何種關系?學生思考后可能會回答:全等三角形的對應邊相等、對應角相等,追問:大家是否能夠直接從記作中判斷出所有的對應點、對應角與對應邊?提示他們運用符號語言來表示,如因為△ABC≌△DEF,所以∠A=∠D,∠B=∠E,∠C=∠F,AB=DE,BC=EF,AC=DF.然后教師組織學生以小組為單位展開合作學習,并親自動手操作,使一個三角板圍繞某頂點進行旋轉,根據操作畫出不一樣的位置關系.如圖4所示,找出兩個全等三角形的對應點、角、邊,學生發現不管哪種圖形,點A與點A是對應頂點,點B與點E是對應頂點,點C與點D是對應頂點;AB邊與AE邊是對應邊,AC邊對應AD邊,DE邊則對應CB邊;∠BAC的對應角是∠EAD,∠B的對應角是∠E,∠C的對應角是∠D,同時讓學生歸納找出全等三角形對應邊、角的竅門,如(1)大邊、大角分別對應大邊、大角;(2)兩個三角形的公共邊、公共角屬于對應邊、角,對頂角屬于對應角,等等.
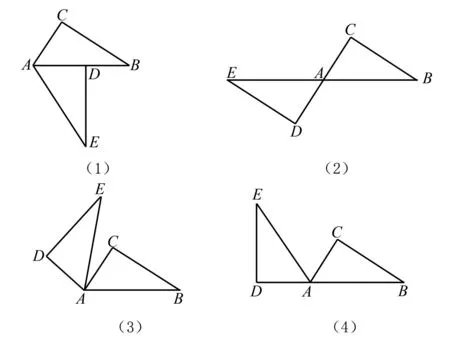
圖4 一塊三角板繞著一個頂點旋轉的四種位置關系
隨后教師設置練習題:已知△ABE≌△ACD,如圖5所示,其中∠ADE=∠AED,∠B=∠C,那么這兩個三角形其它對應角與對應邊分別是什么?學生結合剛才所學的全等三角形的性質在小組內討論和交流后找出對應關系,即為:∠BAD=∠CAE,∠ADB=∠AEC,AB=AC,AD=AE,BD=CE.由此,進一步培養他們對圖形的識別能力,深化理解和掌握全等三角形的性質,同時改善小組協作學習能力與團隊意識.
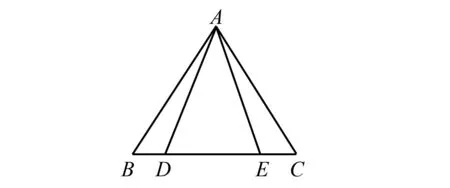
圖5 △ABE≌△ACD
2.3 設計變式,講評例題
教師利用信息技術手段,以動畫形式演示出兩個全等三角形通過變換產生不一樣組合的情況,出示問題:
(1)利用全等符號把圖6中所有的全等三角形找出來;
(2)指出在(1)中找到的全等三角形的對應關系.
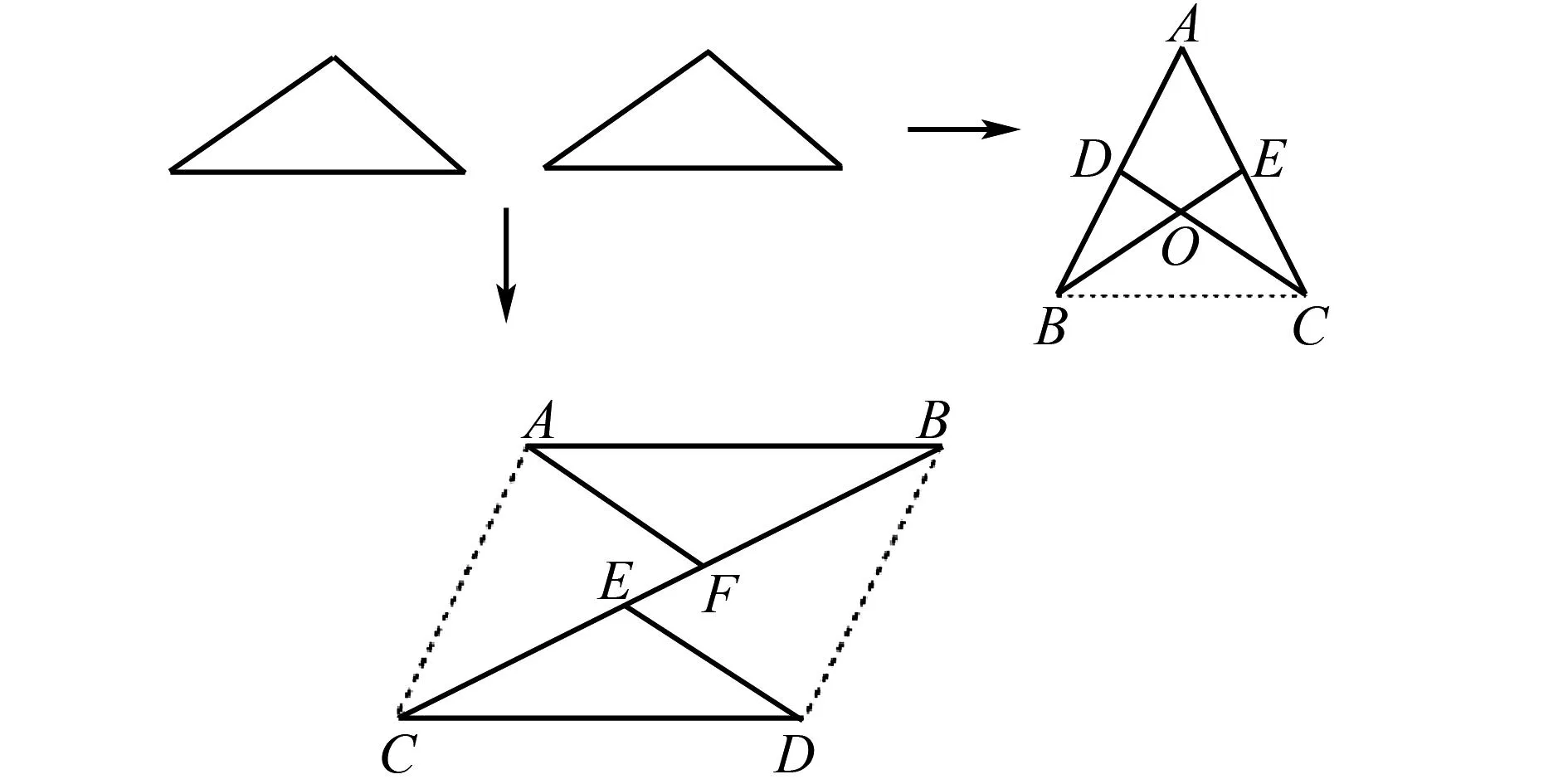
圖6 多個全等三角形
學生觀察、思考以后將會寫出以下答案:
(1)全等三角形有△ABE≌△ACD,△ABF≌△DCE.
(2)在△ABE≌△ACD中,∠ABE=∠ACD,∠AEB=∠ADC,∠A是兩個三角形的公共角,AB=AC,AE=AD,BE=CD;在△ABF≌△DCE中,∠ABF=∠DCE,∠AFB=∠DEC,∠BAF=∠CDE,AB=DC,AF=DE,BF=CE.
接著,教師設計變式練習:
(1)在圖6中,設CD和BE相交于點O,如果△BDO≌△CEO,請指出這兩個三角形的對應角與對應邊;
(2)在圖6中,把BC連接起來,寫出一組全等三角形,并寫出這兩個全等三角形的的對應角與對應邊;
(3)在圖6中,把AC、BD連接起來,你們還可以找到哪幾組全等三角形?并明確對應關系.
學生能夠得出下列結果:
(1)在△BOD≌△COE中,∠BOD=∠COE,∠DBO=∠ECO,∠BDO=∠CEO,BD=CE,BO=CO,DO=EO;
(2)△BCD≌△CBE,∠BCD=∠CBE,∠BDC=∠CEB,∠CBD=∠BCE,BC=CB,即為這兩個全等三角形的公共邊,BD=CE,CD=BE;
(3)△ACF≌△DBE,∠ACF=∠DBE,∠CFA=∠BED,∠CAF=∠BDE,AC=DB,AF=DE,CF=BE.
2.4 課堂小結,深化認知
在本環節中,教師帶領學生一起總結全等三角形中尋找對應角、邊關系的竅門.如在兩個全等三角形中,大邊或者大角對應的便是大邊或者大角),對頂角與公共角都屬于對應角,公共邊屬于對應邊,等等.
總的來說,在大概念下的初中數學幾何章起始課教學活動中,教師應對章起始課高度重視與格外關注,要投入更多的精力與時間來設計這節課,為學生學習本章知識做好導向工作,實現上文中提到的幾個目標,讓學生對接下來的學習內容充滿強烈的求知渴望,推動他們健康、全面的發展.

