田間試驗4 種防效計算方法比較
羅 崗 張谷豐
(1南通市通州區農業農村局科教站,江蘇 南通 226300;2江蘇省農業科學院,江蘇 南京 210000)
相關研究者對于田間試驗效果的計算,引進和提出了許多計算公式[1-2],多年來在一些試驗實例的計算中,因為出現的某些不盡合理的結果多有爭議[3-4]。但實踐中發現,部分田間試驗效果計算公式是相同的[5],如矯正效果的減退率公式[6]、增長率公式[7]、生存率公式[6]和Henderson-Tilton 公式[6]都是一樣的。
如令:CKo為對照區試驗實施前的觀測值;CKh為對照區試驗實施后的觀測值;PTo為處理區試驗實施前的觀測值;PTh為處理區試驗實施后的觀測值。
減退率計算矯正效果的公式:
生存率(增長倍數)計算矯正效果的公式:
如果將上列公式,稍加整理簡化,其結果都為:
與Henderson-Tilton公式一樣。
公式(1)在田間藥劑試驗中普遍應用,包括殺蟲劑試驗和殺菌劑試驗[8-9]。部分作者在殺菌劑試驗時應用此式[10-11],發現效果受對照區病情增長的影響很大,認為該公式不夠完善[12]。為此,提議用Abbott公式[6]或以初始觀測值改進的Abbott公式[2],楊信東以病害疫情流行呈logestic曲線自然增長,在此基礎上進一步提出了楊信東等[8]公式。上述3種公式可表示為:
Abbott公式:
改進的Abbott公式:
楊信東公式:
本文對上述4 種公式進行比較,通過公式的數學分析、效果理論模擬和田間試驗實例應用,對其適用性和穩定性加以評價。
1 材料與方法
1.1 公式的數學分析
分析4種效果計算方法的數學公式可知,公式(1)中,如果PTh×CKo>PTo×CKh,則計算結果將出現負值;但不論是處理區還是對照區的觀測值下,計算結果均不會出現效果大于100%超越公共認知的情況。
在公式(2~4)中,只要出現PTh-PTo<0 或CKh-CKo<0,分式上下正負值不一的情況,計算結果必定會出現效果大于100%超越公共認知的情況。而在公式中分子部分,不論是(PTh-Pto),還是(PTh-PTo)×CKo,或是(PTh-PTo)×CKo×(1-CKh),只要其值大于分母,則結果都會為負。
1.2 方法的分析比較
1.2.1 Henderson-Tilton 公式以試驗后觀測值增長倍數進行比較,避免了試驗前后觀測值差數出現負值的影響,因而,試驗效果不會出現超過100%超越公共認知的結果。雖然有出現效果為負的可能,但出現的概率較低。
1.2.2 Abbott 公式只考慮了試驗前后觀測值之差,忽略了試驗前基礎量,及其在試驗過程中對增長量的影響。因此,計算的試驗效果不太穩定,常出現效果為負,或效果超過100%超越公共認知的結果。
1.2.3 以初始值改進的Abbott 公式將試驗前后觀測值的差,除以試驗前的觀測值,這種改進實質是將差值變為增長率。此式雖然重視了試驗前基礎量對效果的影響,但并未改變公式的性質。
試將此公式可進一步轉化:
以降低茶園小貫小綠葉蟬蟲口基數為目的。一是加強茶園管理,及時清除雜草,及時分批勤采,可隨采摘的嫩芽葉帶走大量的卵及低齡若蟲[2];二是12月下旬用石硫合劑晶體150~200倍液封園,可有效降低蟲口基數。
只是將Abbott 公式的處理區與對照區試驗前后觀測值差之比,修正為對照區試驗后觀測值減去Th/To 分之試驗前觀測值,與對照區病情的增長值之比。盡管試驗效果數值有了變化,但與處理區試驗前后觀測值的比例關系差異不大,對處理區試驗前后觀測值變化的影響重視不夠。
1.2.4 楊信東公式增加了(1-CKh)/(1-PTh)的矯正項,令試驗效果大大壓縮了效果大于100%的絕對數值,還減少了出現負值的概率。但是,從上式的數學運算原理看,理論上還是有出現效果大于100%,或效果為負值的可能。
2 結果與分析
2.1 模擬理論效果的比較
分別以CK0在0.99~0.02,以0.01步減;CKh= 1.0(在應用楊信東公式時為0.99,避免效果都為0);PT0在0.02~0.99,以0.01 步增;PTh起步值為0.01,而后從0.1 起以0.1 為一個級差,增至PTh=1 為止;再以CK0在0.01~1.00,以0.01 步增;CKh=1.0(在應用楊信東公式時為0.99,避免效果都為0);PT0在0.010~0.505,以0.005 步增;PT0起步值為0.01,而后從0.1 起以0.1 為一個級差,到PTh= 1(應用楊信東公式時為0.99)為止,分別計算4 種公式的理論效果,如表1 所示。
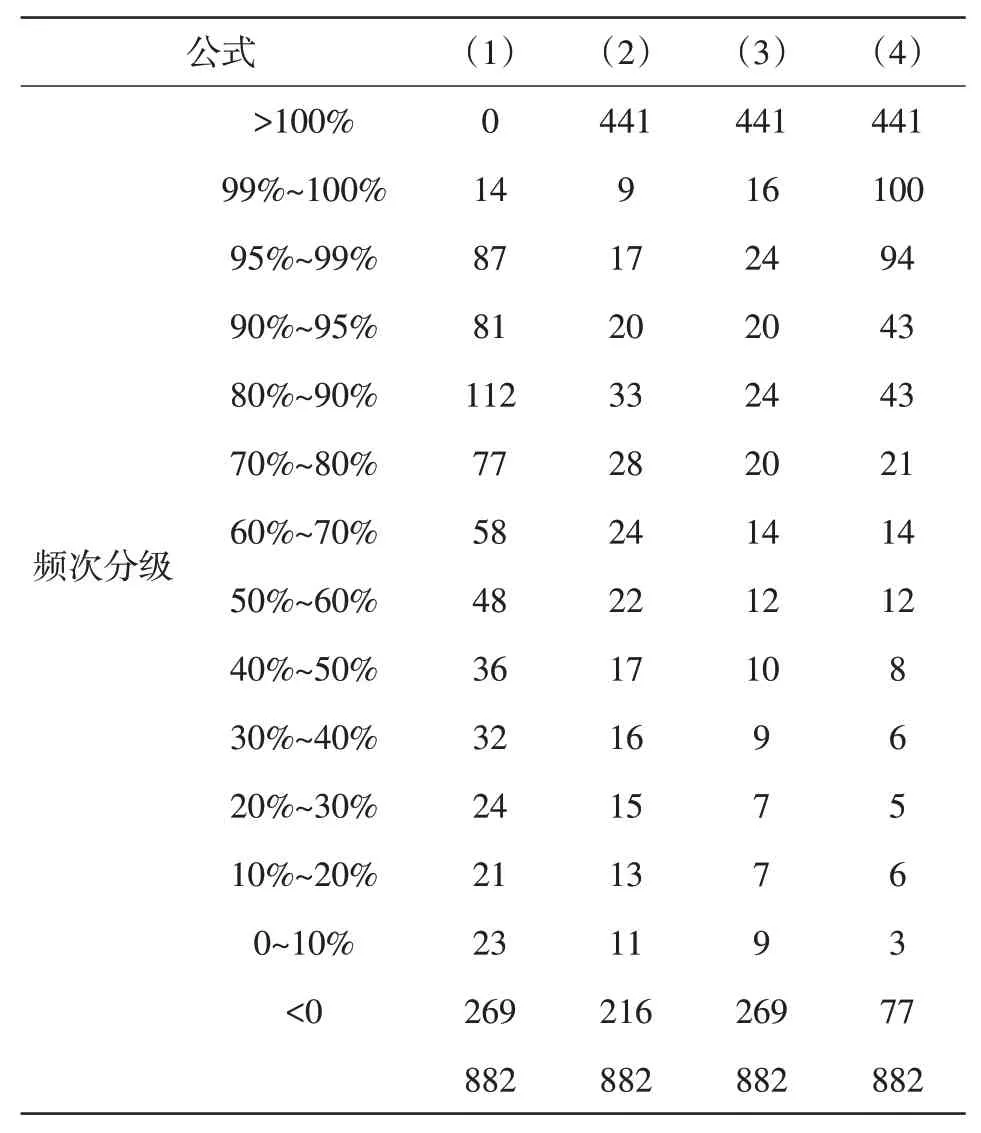
表1 設定條件下4種公式計算的效果分布頻次
對上述兩組設定數值變動范圍,所得理論效果進行分類統計,計數效果>100%,效果介于0 和100%(包括0 和100),以及效果為負值的出現次數。以介于0 和100%的效果作為有效值。各公式所占比例分別為(1)70.50%、100%;(2)25.88%、45.54%;(3)20.50%、27.36%;(4)37.57%、71.90%。公式(3)的改進對理論效果的適合性并未見有所改善,如表2所示。另外,從所得的極值比較,公式(1)變動幅度最小的,而且公式(1)的理論效果的有效率最高,可見其計算結果是4個公式中最為穩定的。
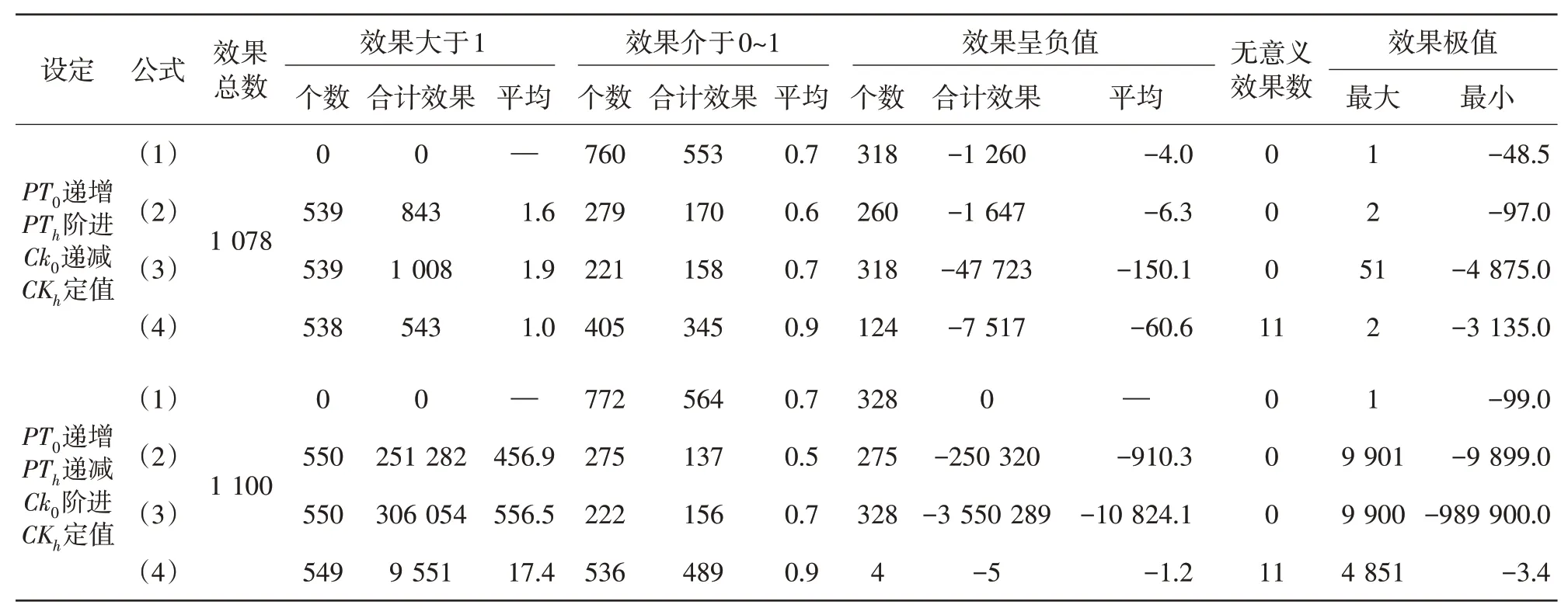
表2 設定數值下4種公式之理論效果適合性比較
2.2 模擬理論效果介于0~1的區段比較
為了比較4種公式計算之效果在0~1的區域,讓(A)PTh于0.02~0.99 漸增,CKo于0.99~0.02 范圍內漸減,以及讓(B)PTh與CKo作相反增減時的理論值計算的基礎上,切取部分區段的結果,制成線性坐標。
由圖1可見,公式(1)介于0~1的區段最大,且只在PTh很小或很大時才出現負值。而公式(2~3)介于0~1 的區段較小,超過1 和小于0 的區段很大;公式(2)在坐標圖上出現兩段背離的曲線,CKh和CKo值愈接近效果距離0~1 越遠,當CKh和CKo相等時效果無意義。公式(4)介于0~1 的區段較大,超過1 的區段也較大,但溢出值不是太大,和公式(1)相似,只在PTh很小或很大時才出現負值。
2.3 田間試驗觀測值的比較
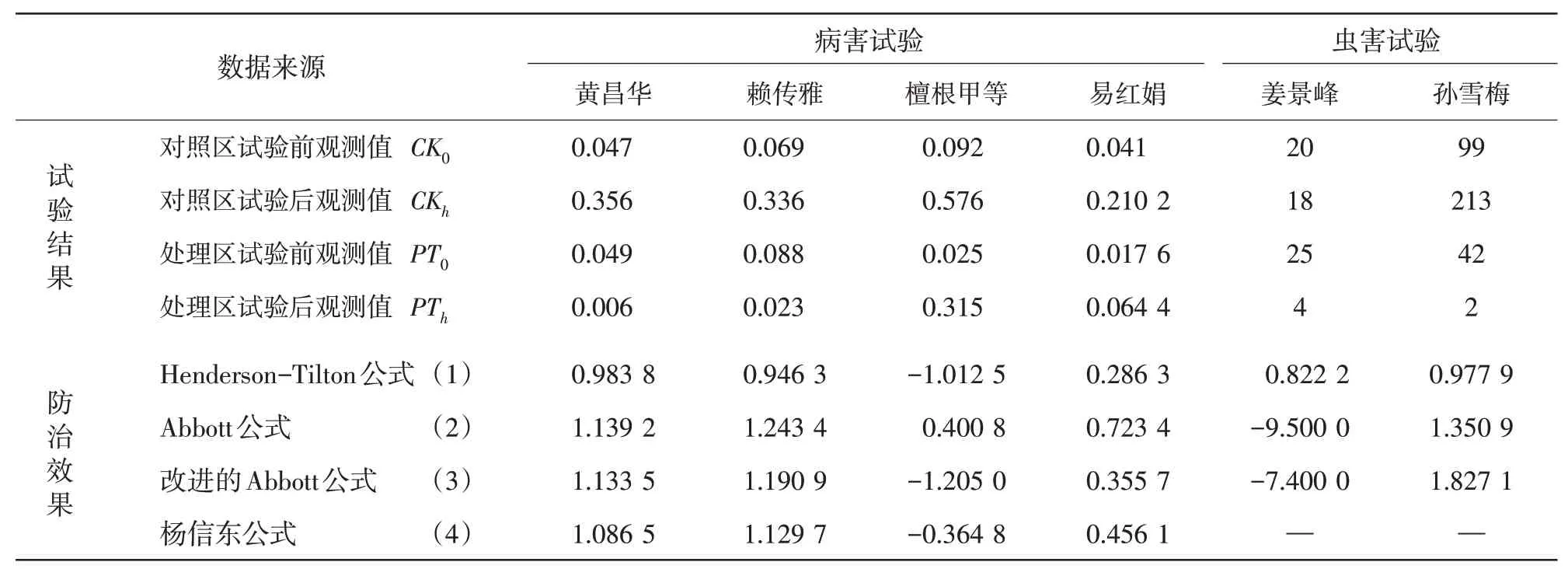
表3 文獻中試驗數據防效計算比較
從計算結果可見,對一些特殊的試驗結果,公式(2~4)多未能解決效果為負或效果大于100%的問題,且不適宜用于害蟲防治試驗。而公式(1)僅在個別實例中出現負值。其他病蟲試驗實例均表現出較好的適用性。
2.3.2 以相同田間試驗的觀測值進行計算南通市通州區植保站于2021年進行了白粉病藥劑防治試驗,試驗設7 個處理加對照,3 次重復,共24 個小區。于試驗前和藥后14 d 調查試驗效果。以用4 個公式計算各重復的調查數據計算防治效果,對各重復調查數據的平均值,同樣進行計算比較。結果如表4—5所示。
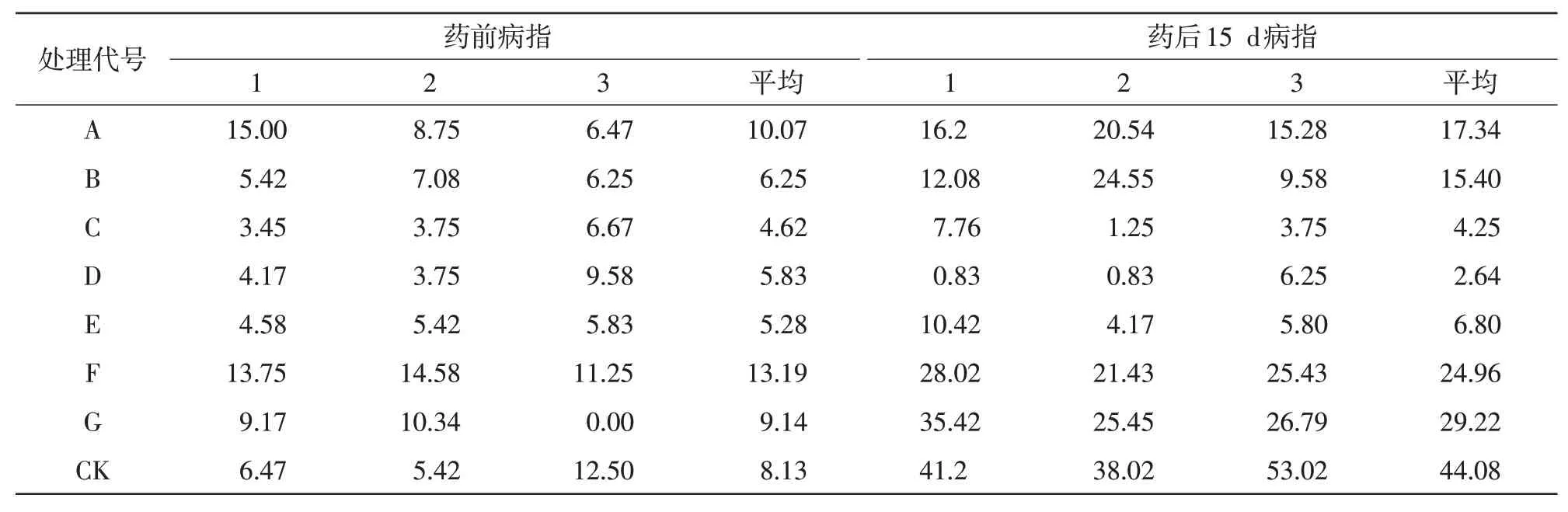
表4 南通市通州區植保站2021年防治白粉病試驗調查結果
由表5可見,公式(1)所得之效果,數值最小,但是最為穩定,均介于0~1。而其余3種方法計算的效果,雖然多數比公式(1)效果好,但多個小區的效果出現超過100%的溢升,超越公共認知之外,而且不能對防效進行反正弦角度轉換,無法將試驗結果進行后續的方差分析。
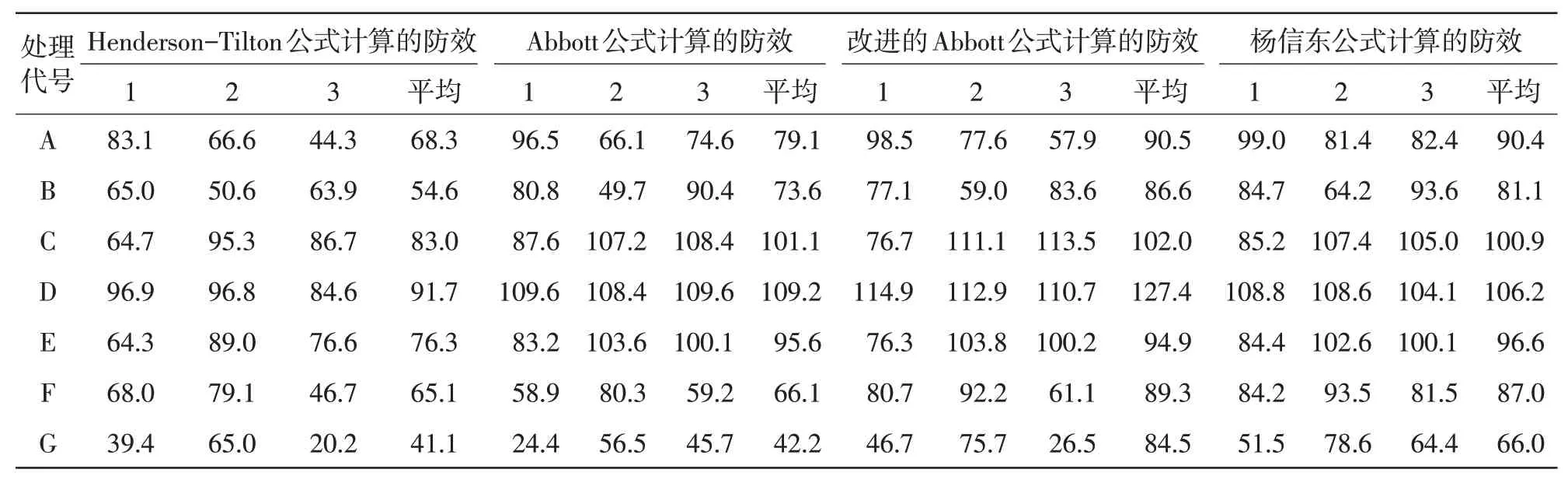
表5 4種方法計算的效果比較
3 結論與討論
3.1 4種公式計算的效果
效果計算公式均由Abbott 公式演化改進而來,但Abbott 公式和楊信東公式只是對原式的改進,在出現效果溢升時表現出同一性。楊信東公式對減少負值出現的確有很大改善,提高了穩定性。Henderson-Tilton公式以增長倍數取代了差值,避免了差值為負的弊端,雖然仍難免有負值的情況出現,但是多出現在試驗初始時病情較輕,處理區與對照區病情差異較大所致。將4 種公式的數學運算的理論分析、模擬數據計算的理論效果,以及田間試驗數據的實際應用進行比較,本研究認為Henderson-Tilton公式計算的效果最為穩定,且計算便捷,適用面廣,病害和蟲害的藥劑試驗都能用。
3.2 計算結果的誤差
由于4 種公式對計算參數處理方式不一,可能出現計算結果的誤差[13]。但是,在田間進行的試驗效果,除受到試驗標的物的影響外,還會受到供試對象的健康情況、環境因子的變化等非試驗因素的影響。田間試驗效果只是一個提供比較的相對指標,并非高精度的測量指標,所以無須過分追求計算結果的精確性。用來計算效果的基本數據,就是同一田間的調查數據,本身就存在較大的隨機誤差。由于不同病害田間病情分布的格局不一,其調查結果除人為因素外,還會因調查樣本的大小、樣點的多少、取樣方法、樣點的位置乃至調查人員的變動,而引起基本數據的變化。因此,應著力提高調查數據的代表性和可靠性,如力求試驗區作物長勢、肥力水平相似,試驗期間管理措施一致,調查時增加樣本量、采用標記定點等技術手段,以及防止產生人為誤差等,可以通過增加重復次數來實現較精準試驗效果。
綜上,Henderson-Tilton 公式的計算結果最為穩定、適用面廣且計算便捷。Henderson-Tilton 公式以增長倍數取代了試驗前后的差值,避免了效果出現超過100%的溢升。而Abbott 公式、以增長率取代差值后改進的Abbott 公式、楊信東公式均存在差值項,當差值為負時,效果必將出現超過100%的溢升,不利于試驗結果的后續分析。

