礦用設(shè)備的振動信號數(shù)據(jù)分析

朱姍姍, 張欣怡, 廖雪梅

(1.北京工業(yè)職業(yè)技術(shù)學(xué)院機電工程學(xué)院, 北京 100042; 2.中國科學(xué)院自動化研究所, 北京 100083;3.首鋼工學(xué)院機電工程學(xué)院, 北京 100042)

1 前言

礦用機械設(shè)備的工作環(huán)境比較復(fù)雜,工作運行過程中很容易發(fā)生振動[1]。一旦設(shè)備中的部件由于振動引起機器故障,則會引發(fā)安全事故[2]。通常情況下,很難觀查到設(shè)備內(nèi)部構(gòu)件運動狀態(tài)的異常,很難預(yù)判機器發(fā)生故障的部位[3]。為了檢測設(shè)備的運行狀態(tài),可以通過在礦用設(shè)備上安裝傳感器來檢測各個部件的工作參數(shù)。根據(jù)傳感器檢測數(shù)據(jù)的變化,可以有效地預(yù)判故障的發(fā)生,從而保證生產(chǎn)的安全[4]。

礦用設(shè)備除了工作環(huán)境復(fù)雜,引起振動的情況錯綜復(fù)雜,環(huán)境測試和故障分析工作難以開展外[5]。有些設(shè)備的振動信號變化非常快,例如旋轉(zhuǎn)機械的故障信號,這些信號的變化速度往往超過了人類的感知速度,使得故障分析工作非常困難[6]。有些設(shè)備的振動信號非常微弱,這會造成有效的信號往往被噪聲淹沒,使得故障分析的工作難度進(jìn)一步加劇[7]。同時,有些設(shè)備的振動信號會受到多種干擾源的影響,例如電磁干擾、溫度變化等,這些干擾源使得信號難以被準(zhǔn)確地測量和分析[8]。另外,有些設(shè)備的振動信號具有非線性特性,例如摩擦故障、碰撞故障等,這些非線性特性使得信號難以被傳統(tǒng)的線性分析方法所捕捉[9]。許多學(xué)者對礦用設(shè)備的振動特性進(jìn)行了研究。文獻(xiàn)[10-12]對采煤機螺旋滾筒建立了有限元模型,結(jié)合神經(jīng)網(wǎng)絡(luò)模型,分析了結(jié)構(gòu)參數(shù)對振動可靠性的影響。文獻(xiàn)[13-16]建立了采煤機側(cè)向6個自由度的動力學(xué)模型,并采取數(shù)值分析的方法,求解了不同煤巖硬度對側(cè)向振動的影響。

對于采礦設(shè)備的實際工況中,發(fā)生單個振動的情況在實際生產(chǎn)過程中并不常見,實際工況中發(fā)生的大多數(shù)振動是兩個或兩個以上的振動的合成[17]。而在分析振動情況和研究振動信號時,通常需要分別分析各個因素對設(shè)備產(chǎn)生振動的影響,在振動信號的提取和數(shù)據(jù)分析方面,需要對在復(fù)雜工況下設(shè)備的振動信號先進(jìn)行降噪處理,再對有效的信號或者分析目標(biāo)進(jìn)行數(shù)據(jù)篩選。本文以采煤機搖臂為研究對象,采集搖臂振動信號,將采集得到的搖臂振動信號樣本輸入到神經(jīng)網(wǎng)絡(luò)中進(jìn)行學(xué)習(xí),將學(xué)習(xí)好參數(shù)的神經(jīng)網(wǎng)絡(luò)模型應(yīng)用于輸出振動測試結(jié)果。通過對搖臂的模擬試驗和數(shù)據(jù)分析,可以研究影響設(shè)備振動的變量關(guān)系,有效地預(yù)判機器故障。

2 搖臂系統(tǒng)振動模型

采煤機搖臂的結(jié)構(gòu)如圖1所示。對搖臂的振動微分方程進(jìn)行分析時,將采煤機的滾筒部件簡化成集中質(zhì)量塊,將搖臂部件簡化成懸臂梁,受力如圖2所示。

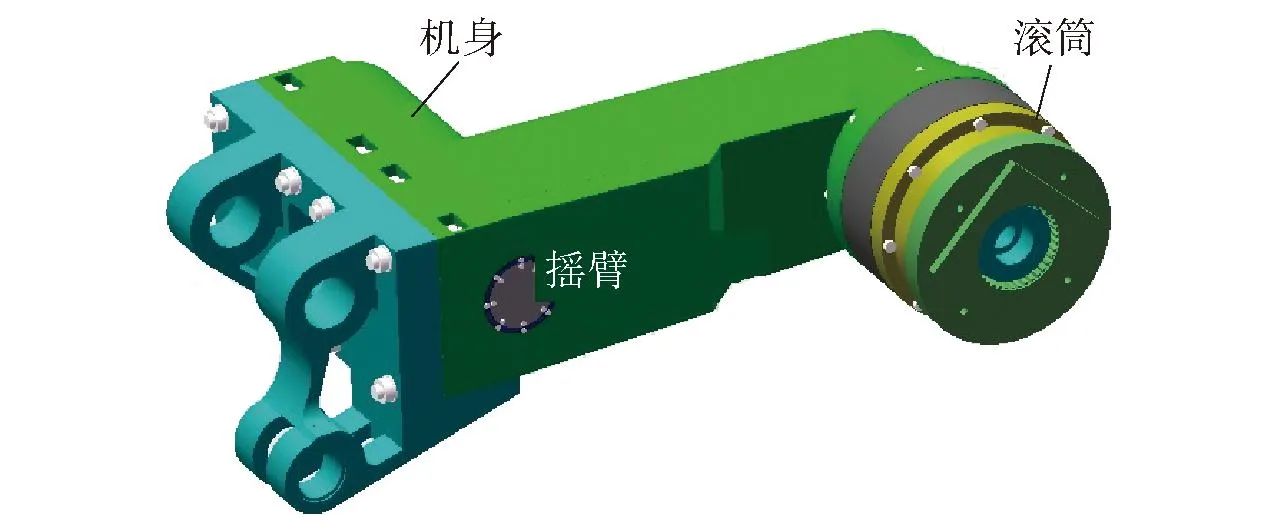
圖1 采煤機結(jié)構(gòu)示意圖

圖2 等效轉(zhuǎn)換后搖臂受力分析示意圖

懸臂梁的失效形式主要有剪切破壞、彎曲破壞和扭轉(zhuǎn)破壞[18]。本文以礦用設(shè)備中的采煤機為例,分析其搖臂部件的橫向振動,振動微分方程可表示為

(1)

E為懸臂梁材料的彈性模量,I為搖臂橫截面的慣性矩,ω為固有頻率,Φn為模態(tài)。把響應(yīng)按照模態(tài)進(jìn)行展開。

(2)

將式(2)代入式(1),可得

(3)

式(3)兩邊同乘以Φm(x),并沿梁全長進(jìn)行積分,可得

(4)

利用模態(tài)正交性,式(4)可解耦為

(5)

假設(shè)在時間t=0時的初始條件為

(6)

對于初始條件式(6),也通過式(2)進(jìn)行展開,即

(7)

(8)

根據(jù)上式等號兩邊同乘以ρAΦn(x),ρ為材料的密度,A為橫截面積。并沿桿長度對x進(jìn)行積分,利用模態(tài)正交性可得

(9)

(10)

與直桿的縱向振動類似,式(5)的解可以表示為

(11)

在此基礎(chǔ)上,如果考慮梁的阻尼影響,式(5)可以重新表示為

(12)

式中,ζn表示第n階模態(tài)的阻尼比。

假設(shè)激勵力為作用在梁x=x0處的集中力f(t),則廣義模態(tài)力為

(13)

首先引入狀態(tài)向量y,

(14)

取前N階模態(tài)進(jìn)行計算,則式(12)可表示為

(15)

假設(shè)要輸出的是在梁上x=xs點的位移響應(yīng),由式(2)可知:

(16)

3 振動信號的采集與預(yù)處理

3.1 振動信號采集的模擬實驗裝置

為了采集搖臂橫向振動模型的振動信號,建立振動信號的樣本集,通過神經(jīng)網(wǎng)絡(luò)算法,將搖臂的振動信號輸入層與輸出層構(gòu)建一定的輸入、輸出的函數(shù)關(guān)系,開展搖臂模態(tài)試驗,設(shè)計了以鋼板代替搖臂的實驗臺,用夾持機構(gòu)夾緊鋼板的一端,在鋼板的末端安裝激振器,測試實驗臺如圖3所示,以模擬采煤機滾筒的截割激勵;同時在鋼板末端安裝壓電式加速度傳感器來采集鋼板的振動信號,將傳感器采集到的振動信號傳輸?shù)捷斎雽印?/p>

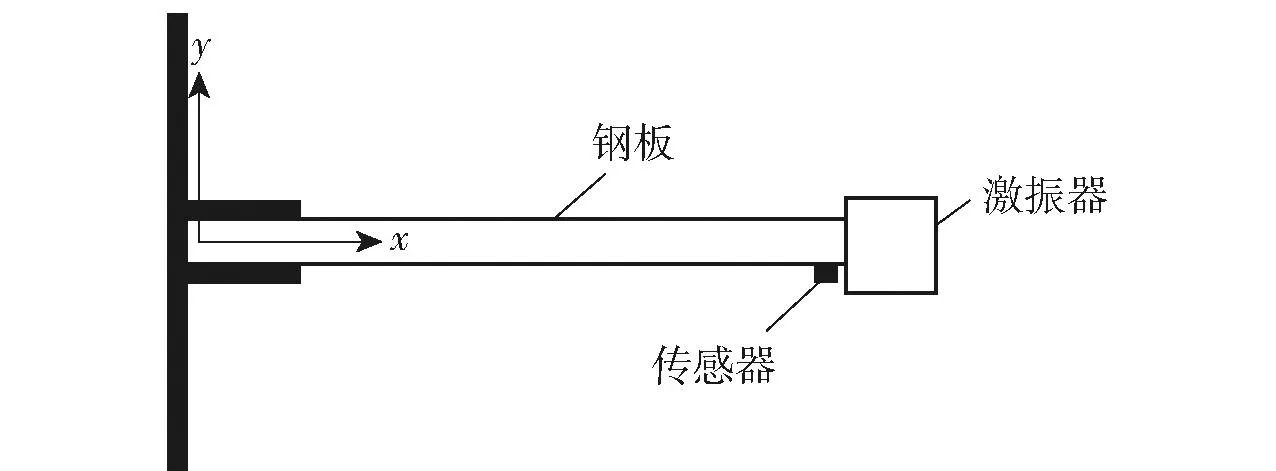
圖3 搖臂振動測試實驗臺

3.2 振動信號的采集

為給搖臂振動系統(tǒng)采集充分的數(shù)據(jù)樣本,通過改變鋼板的長度及激勵力的大小來獲取不同的振動信號。通過將采集的振動信號處理成機器學(xué)習(xí)的樣本集,應(yīng)用神經(jīng)網(wǎng)絡(luò)建立振動輸入層與輸出層之間的函數(shù)關(guān)系,擬合實際振動發(fā)生的情況。圖4、圖5所示為激勵力頻率為ω=2 Hz,鋼板長度為1 m,抗彎強度EI=36 N/m,模態(tài)阻尼比為0.01,通過狀態(tài)空間法分析激勵力分別為1 N、2 N作用下的時域響應(yīng)。同樣,可以跟換鋼板的長度、改變激勵力頻率等方式獲取不同工況下?lián)u臂的工作狀態(tài);圖6、圖7所示為激勵力頻率為ω=2 Hz,鋼板長度為2 m,抗彎強度EI=36 N/m,模態(tài)阻尼比為0.01,通過狀態(tài)空間法分析激勵力分別為1 N、2 N作用下的時域響應(yīng)。通過模態(tài)進(jìn)行計算時,即可獲得足夠的計算精度。

圖4 激勵力=1 N、L=1 m時振動信號

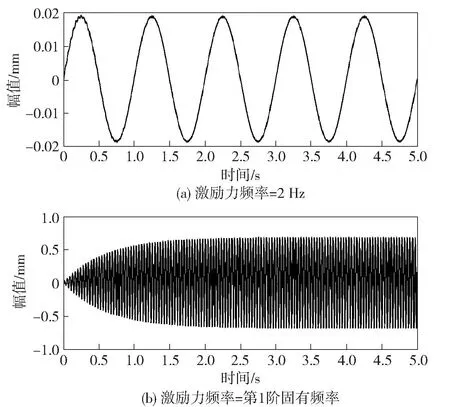
圖5 激勵力=2 N、L=1 m時振動信號

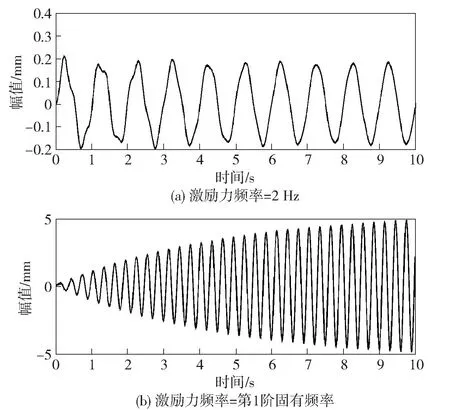
圖6 激勵力=1 N、L=2 m時振動信號

圖7 激勵力=2 N、L=2 m時振動信號

4 振動信號的數(shù)據(jù)分析

將實驗中采集到的不同振源產(chǎn)生的振動信號建立樣本集。輸入到神經(jīng)網(wǎng)絡(luò)進(jìn)行學(xué)習(xí),通過擬合曲線不斷迭代修正,建立輸入變量與輸出之間的函數(shù)關(guān)系。相當(dāng)于產(chǎn)生了一個近似函數(shù)來擬合輸入層中的每一組實驗數(shù)據(jù)。擬合函數(shù)計算得出的輸出值越接近實驗中的測量值,說明網(wǎng)絡(luò)模型分析的數(shù)據(jù)越接近實際情況[19]。在Python擴展庫中實現(xiàn)了多種線性回歸和非線性回歸的模塊,scipy和statsmodelds擴展庫中也有實現(xiàn)了多種回歸分析的模塊[20]。應(yīng)用numpy擴展庫的多項式擬合函數(shù),也可以完成回歸分析的模型參數(shù)估計的工作。為驗證權(quán)重值的取值誤差,選取2組實驗實測輸出信號與神經(jīng)網(wǎng)絡(luò)推算的輸出結(jié)果進(jìn)行比較,比較結(jié)果如圖8、圖9所示。

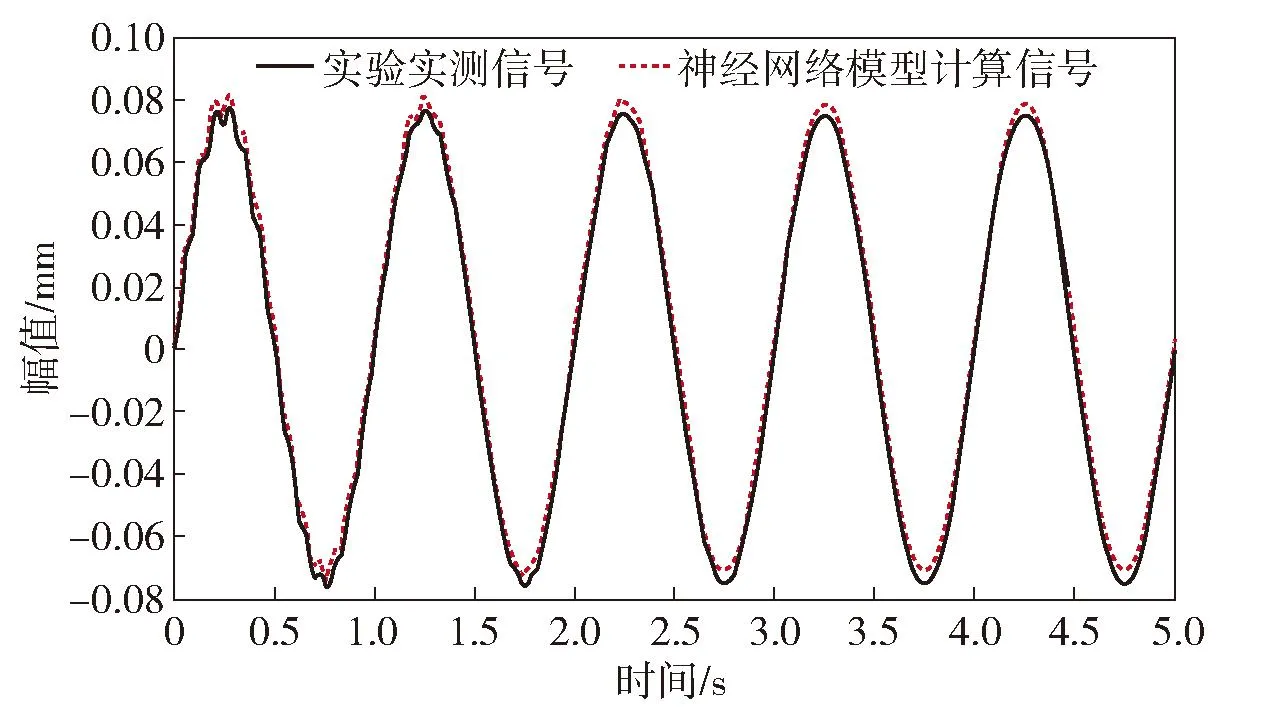
圖8 激勵力=1 N、L=1 m時實測信號與計算數(shù)據(jù)對比

圖9 激勵力=1 N、L=2 m時實測信號與計算數(shù)據(jù)對比

圖8所示為應(yīng)用scipy.stats.linregress()處理一維數(shù)據(jù)的最小二乘回歸,模型返回模型系數(shù)。Scipy.stats.linregress()函數(shù)提供了一個簡單的接口,可以方便地進(jìn)行線性回歸分析,只需要提供數(shù)據(jù)和參數(shù)即可。Scipy.stats.linregress()函數(shù)采用了高效的數(shù)值計算方法,可以快速地進(jìn)行回歸分析,并且可以處理大規(guī)模的數(shù)據(jù)集,可以用于多種不同的線性回歸模型,用戶可以根據(jù)需要選擇合適的模型,提供豐富的功能,包括計算回歸方程、回歸系數(shù)的標(biāo)準(zhǔn)誤差等,可以幫助用戶深入分析回歸結(jié)果。在數(shù)據(jù)應(yīng)用方面,Scipy.stats.linregress()函數(shù)可以用于預(yù)測分析,預(yù)測因變量的值,幫助用戶進(jìn)行決策;可以評估各個自變量對因變量的影響程度,幫助用戶選擇最有價值的自變量;可以檢測數(shù)據(jù)集中是否存在異常值,幫助用戶提高數(shù)據(jù)質(zhì)量。

圖9所示為應(yīng)用numpy.linalg.lstsq()獲得擬合函數(shù),Numpy.linalg.lstsq()是Python中用于求解線性最小二乘法問題的庫函數(shù)。只需要提供數(shù)據(jù)和參數(shù)可以快速地進(jìn)行回歸分析,并且可以處理大規(guī)模的數(shù)據(jù)集,包括簡單線性回歸、多元線性回歸等,用戶可以根據(jù)需要選擇合適的模型,得到的回歸系數(shù)具有較高的精度用于預(yù)測分析、相關(guān)性分析、特征選擇及異常值檢測等,快速將有效的數(shù)據(jù)信息分析提供決策支持。

從圖8、9看出,選用不同算法擬合的函數(shù)在與實測振動信號的對比顯示,兩種算法建立的模型有一定的參考依據(jù)。卷積神經(jīng)網(wǎng)絡(luò)算法用于采煤機搖臂振動信號的數(shù)據(jù)采集、分析與處理,建立的算法模型有效地擬合了實驗采集的振動信號樣本,可用于振動信號的模態(tài)分析及預(yù)測、影響振動的參數(shù)變量與輸出信號的相關(guān)性、特征選擇及異常值檢測。

5 結(jié)論

礦用設(shè)備除了設(shè)備工作環(huán)境復(fù)雜,振動和故障分析工作面臨著多種挑戰(zhàn)。本文對礦用設(shè)備振動信號的數(shù)據(jù)分析,得出以下結(jié)論。

(1)根據(jù)礦用設(shè)備實際工況中復(fù)雜的工作特性,設(shè)計了模擬采煤機搖臂振動信號的實驗臺;實驗采集了搖臂在各種工況下的振動信號,建立了搖臂橫向振動數(shù)據(jù)分析的網(wǎng)絡(luò)模型,可以自動地分析處理輸入數(shù)據(jù)的特征,有效地提取采煤機搖臂振動信號中的有效數(shù)據(jù),與輸出信號建立函數(shù)關(guān)系擬合實測信號。

(2)通過對搖臂振動響應(yīng)的數(shù)據(jù)采集與模態(tài)分析,應(yīng)用不同的算法對比,在一定誤差范圍內(nèi)擬合了搖臂橫向振動模型。建立的神經(jīng)網(wǎng)絡(luò)可以擴展到多層結(jié)構(gòu),從而處理更加復(fù)雜的振動信號;同時卷積層和池化層可以學(xué)習(xí)到搖臂振動輸入信號的空間特征和特征變換,從而可以解釋網(wǎng)絡(luò)的輸出結(jié)果,有利于分析和理解采煤機搖臂振動信號的參數(shù)變量之間的函數(shù)關(guān)系。

(3)通過神經(jīng)網(wǎng)絡(luò)可以自動進(jìn)行特征提取和數(shù)據(jù)分類,無需人工干預(yù),從而大大減少人工分析的工作量和誤差,為礦用設(shè)備工作狀態(tài)監(jiān)測與故障預(yù)判提供數(shù)據(jù)依據(jù)。