定積分微元法的教學探析與思考

李靈曉 黃元元 王鋒葉

摘?要：本著教育數(shù)學的思路，結(jié)合分析和比較三種微元法觀點探析定積分微元法的主要思想，總結(jié)出定積分微元法的使用特點及判定方法，并運用微元分析法解決曲邊扇形面積和變力對質(zhì)點的沖量兩個問題，該方法類似可推廣到其他幾何、物理及經(jīng)濟問題.

關(guān)鍵詞：高等數(shù)學；定積分；微元法；高階無窮小；教育數(shù)學

中圖分類號：G642??文獻標識碼：C

Exploration?and?Reflection?on?the

Teaching?of?Differential?Element?Method?of?Definite?Integral

Li?Lingxiao?Huang?YuanYuan?Wang?FengYe

School?of?Mathematics?and?Statistics，Henan?University?of?Science?and?Technology?HenanLuoyang?471000

Abstract：According?to?the?idea?of?educational?mathematics，this?paper?analyzes?the?main?ideas?of?definite?integral?differential?element?method，combined?with?the?analysis?and?comparison?of?three?viewpoints?of?differential?element?method.The?application?characteristics?and?judgment?methods?of?definite?integral?and?differential?element?method?are?summarized.The?differential?element?analysis?method?is?used?to?solve?the?two?problems?of?the?sector?area?of?the?curved?edge?and?the?impulse?of?the?variable?force?to?the?mass?point.This?method?is?similar?and?can?be?extended?to?other?geometric，physical?and?economic?problems.

Keywords：advanced?mathematics；difinite?integral；differential element?method；infinitesimal?of?higher?order；educational?Mathematics

1?概述

大學數(shù)學教育的任務(wù)，就是運用教育數(shù)學的思路，將已有的數(shù)學成果進行再創(chuàng)造，適當?shù)馗倪M數(shù)學表述形式，使之更加科學、更加適合于教學［1］。高等數(shù)學教材就有很多這樣的概念，既經(jīng)典又凝練，如何優(yōu)化其概念表述方式讓它更適合學生接受？這也是我們數(shù)學教育工作者值得思考的一個問題。文獻［2］對于數(shù)學知識的結(jié)構(gòu)和表現(xiàn)方法提出以下三條標準：（1）邏輯結(jié)構(gòu)盡可能簡單；（2）概念引入要平易直觀；（3）要建立有力而通用的解題工具.這也是教育教學追求的主要目標.

在解決幾何、物理、經(jīng)濟等領(lǐng)域中的一類實際問題時，往往用定積分來解決，而微元法（或“元素法”）正是解決該類問題過程中最常用及最方便的方法。什么是微元法？不同的教材有不同的表述方法，而不同的教師又有不同的理解，但大多表達較為隱晦而凝練，學生接受起來有一定的難度.本文首先結(jié)合分析三種微元法觀點來討論微元法的主要思想（可參閱文獻［39］，尤其是文獻［5］），其次給出微元法的使用特點、判定方法，最后給出兩個相關(guān)幾何和物理應(yīng)用.

2?有關(guān)微元法的不同表述

2.1?概念定義法

微元法實質(zhì)上就是定積分定義中的三步法——分割、近似求和、取極限的簡化，其理論基礎(chǔ)是定積分的定義及被積函數(shù)的可積性.這種說法雖然理論上無懈可擊，但在敘述及方法的運用上過于煩瑣、零碎，而且對一些物理量（如質(zhì)量、轉(zhuǎn)動慣量、引力）的大小用定義給出的方法有點兒勉強，因為這些量都是客觀存在的，它們量值的大小是不以人的主觀定義而改變的.因而這種說法的合理性還須保證相應(yīng)的定義的合理性.

2.2?物理直觀法

這種方法采用牛頓、萊布尼茨當時創(chuàng)立微積分時對定積分是所謂對無窮小量（微元）的加法的思想.具體地講，就是要計算一個實際量I，先將這個量分成部分量的和I=∑ΔI，再通過尋找函數(shù)f（x），求得部分量的一個線性（關(guān)于Δx的）近似表達式ΔI≈f（x）Δx，這里一般要求f（x）連續(xù)，f（x）Δx就是實際量I的一個（積分）微元（元素）.從而I=∑ΔI≈∑f（x）Δx，這里∑表示對離散量求和，將其換為對連續(xù)量求和即定積分就得到了實際量I的計算公式I=∫baf（x）dx.這種方法直觀、簡潔、有效，被現(xiàn)在大多數(shù)的物理學家或物理教師所采用，但其并不具有數(shù)學的嚴格性，因為它并沒有說清楚為什么把∑換為∫，就把一個原本是近似的等式變成了精確等式，這種缺陷也是微積分初創(chuàng)時期備受指責的原因之一.雖然在物理上可以通過數(shù)據(jù)去驗證等式，從而彌補此缺陷，但這不能兼容于數(shù)學家（數(shù)學家和物理學家往往在嚴謹性方面理解不同，數(shù)學家認為，一百個實際驗證也不會比一個理論證明更可信；而物理學家則覺得一百個理論證明也比不上一個實際驗證更可靠）.

2.3?微分推導法

這種方法吸收以上兩種方法優(yōu)點，既有物理的直觀，又有數(shù)學的嚴謹.具體說來就是：要計算一個實際量I，這個量必須具有兩個特性：（1）I是一個與某變量x的變化區(qū)間［a，b］有關(guān)的量，即量I是一個分布在區(qū)間［a，b］上的整體量；（2）I對于［a，b］具有可加性，即I=∑ΔI.在（1）、（2）基礎(chǔ)上，為了求實際量I，需建立一個關(guān)于I的函數(shù)I（x）（常稱之為分布函數(shù)），使得I（a）=0，I（b）=I，且I=∑ΔI，其中應(yīng)該注意：ΔI既是I在［a，b］的子區(qū)間［x，x+dx］上所對應(yīng)的部分量，又是函數(shù)I（x）在子區(qū)間［x，x+dx］上的改變量，即ΔI=I（x+dx）-I（x）.如果能找到f（x），使得ΔI的近似表示式是ΔI≈f（x）Δx，并且ΔI=f（x）Δx+o（Δx），這里o（Δx）表示Δx的高階無窮小（Δx→0），從而函數(shù)I（x）可微，且I′（x）=f（x）或dI=f（x）dx（微元或微分表達式），而f（x）（常稱之為I（x）的密度函數(shù)或邊際函數(shù)）一般要求為連續(xù)函數(shù)，從而就可推得I=∫baf（x）dx.

3?微元法三種表述的關(guān)系及框圖說明

在上述微元法的三種表述中，我們著重分析了它們的區(qū)別，當然我們也可從聯(lián)系和共性的方面來對之進行分析.下面用三行框圖來分別表示上述的概念定義法、物理直觀法及微分推導法，從中也反映了三者間的一些聯(lián)系.

因為概念定義法分割區(qū)間、取i都要求有任意性，求和、求極限又是固定模式，故可簡述其過程，從而就化為物理直觀法：

在微段［x，x+Δx］上，I累積的微量ΔI，代之以微分dI=f（x）dx，（dx=Δx），就可簡化成微分推導法，當然，關(guān)系式ΔI=f（x）Δx+o（Δx）一般不作驗證.

上面三種方法尤其第三種“微元推導法”，其核心可壓縮為以下框圖：

用以上所表示的形式，來解決求實際量I的方法，稱為微元法.在對實際量I建立定積分的微元法中，dI稱之為I的積分微元或積分元素.若量I表示面積，dI就稱為面積微元；若量I表示體積，dI就稱為體積微元；若量I表示質(zhì)量，dI就稱為質(zhì)量微元；等等.應(yīng)該注意，作為實際量的I，它是一個常數(shù)值，如曲邊梯形的面積、旋轉(zhuǎn)體的體積、細棒的質(zhì)量等，但微元dI中的I實質(zhì)上是實際量I的分布函數(shù)，換句話說，這里的符號I也是身兼兩職.

微元法在解決實際問題時具有簡單、直觀、方便的特點，且應(yīng)用廣泛，應(yīng)熟練掌握之.

4?微元法的使用特點

微元法的使用特點即能用定積分計算的量I所須滿足的條件，有下列三條：

①I與某變量x的變化區(qū)間［a，b］（區(qū)間有時也可以是無窮的）有關(guān)；

②I對于區(qū)間［a，b］具有可加性；

③I的部分量ΔI可近似地表示成f（x）·Δx，或者說求得微分表達式dI=f（x）dx.

從上面三個條件可以看出，微元法的關(guān)鍵是求微分表達式或者說微元表達式dI=f（x）dx（這也是我們將這種方法稱為微元法的主要原因），而微元表達式成立的前提是驗證一個高階無窮小：ΔI=f（x）Δx+o（Δx），即證明

limΔx→0ΔI-f（x）ΔxΔx=0（*）

而事實上，要驗證（*）式成立在實際問題中不是一件容易事情，有時驗證（*），其難度甚而超過了找f（x）以及求定積分本身.也正因為此，為了在微元法中不至于“喧賓奪主”，這一條件的驗證往往被略去或者被淡化，這也許是微元法不叫“微分法”的一個緣由吧，當然這同時也是微元法受到質(zhì)疑的原因.

5?微元法中高階無窮小成立的判定方法

如何做到既要保證（*）式成立（嚴謹?shù)男枰植恍枰苯域炞C它（方便的需要）？文獻［10］通過一個求曲邊梯形面積的問題，總結(jié)出一個命題，我們將其改造并推廣為更易于接受的一種數(shù)學表述形式，得到以下兩個判定定理.

定理1（判定法則1）設(shè)I是分布在區(qū)間［a，b］上的一個量，I（x）為區(qū)間［a，b］上的分布函數(shù)，且I（a）=0，I（b）=I，ΔI為I在［x，x+Δx］［a，b］上的部分量，也是I（x）在小區(qū)間上的函數(shù)增量，即ΔI=I（x+Δx）-I（x），若存在一個連續(xù)函數(shù)f（x），使得Δx·mxf（x）≤ΔI≤Δx·Mxf（x），其中Δx>0，mxf（x），Mxf（x）分別是f（x）在［x，x+Δx］上的最小值和最大值，則limΔx→0ΔI-f（x）ΔxΔx=0，即dI=f（x）dx，且I=∫baf（x）dx.

證明：∵f（x）在［x，x+Δx］［a，b］上連續(xù)，

∴mxf（x），Mxf（x）在［x，x+Δx］上是存在的。

由已知條件Δxmxf（x）≤ΔI≤ΔxMxf（x）

從而mxf（x）-f（x）≤ΔI-f（x）ΔxΔx≤Mxf（x）-f（x）

再由f（x）在［x，x+Δx］［a，b］上連續(xù)，

∴當Δx→0時，mxf（x）-f（x）→0，Mxf（x）-f（x）→0

∵由夾逼定理知limΔx→0ΔI-f（x）ΔxΔx=0，即ΔI-f（x）Δx=o（Δx），從而dI=f（x）dx，且I=∫baf（x）dx.證畢.

上面我們討論的是所求量為標量的情況，進一步，我們可將其推廣到矢量的情況.

設(shè)向量A→=A1，A2，A3為所求的實際量，定義A→（x）為相應(yīng)一元向量分布函數(shù)，ΔA→為A→（x）關(guān)于自變量x的子區(qū)間［x，x+Δx］上的改變量，ΔA→=ΔA1，ΔA2，ΔA3，其中ΔA1，ΔA2，ΔA3為ΔA→分別在x軸、y軸及z軸上的標量.

定理2（判定法則2）對ΔAi，若fi（x）為連續(xù)函數(shù)且滿足：

Δx·mxfi

Δx·Mxfi，（i=1，2，3）

則A→=∫Rf→（x）dx，其中f→=f1（x），f2（x），f3（x），mxfi，Mxfi分別為fi在小區(qū)間上的最小、最大值.

證明：∵fi（x）為連續(xù)函數(shù)

∴fi（x）在相應(yīng)坐標軸上的子區(qū)間上都存在最大值Mif和最小值mif

又∵Δxmxfi

ΔxMxfi，

∴由判定法則1可同理得到Ai=∫Rfi（x）dx，（i=1，2，3）

∴A→=A1，A2，A3=∫Rf1（x）dx，∫Rf2（x）dx，∫Rf3（x）dx=∫Rf→（x）dx

到此，我們可以看出，只要所求量滿足判定法則1或2的條件，由定理就可判定可以用微元法將所求實際量化為定積分來計算.

6?用微元法計算實際量I的步驟

設(shè)所求實際量I滿足微元法的使用特點，則可按下列步驟將I化作定積分：

（1）根據(jù)所求問題，選取一個變量x為積分變量，并確定它的變化區(qū)間［a，b］，建立實際量的分布函數(shù)I（x），使得I（a）=0，I（b）=I；

（2）設(shè)想將區(qū)間［a，b］分成若干小區(qū)間，取其中的任一小區(qū)間［x，x+Δx］，找出［a，b］上的非負連續(xù)函數(shù)f（x），使得在［x，x+Δx］上，部分量ΔI有近似關(guān)系ΔI≈f（x）dx；

（3）在子區(qū)間［x，x+Δx］上，驗證條件Δx·mxf（x）≤ΔI≤Δx·Mxf（x），從而可得微元表達式dI=f（x）dx；

（4）以［a，b］為積分區(qū)間，計算定積分I=∫baf（x）dx.

7?微元分析法在幾何中的應(yīng)用——曲邊扇形面積

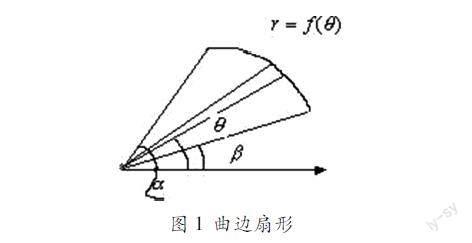
例1：設(shè)由曲線r=f（θ）及射線θ=α，θ=β圍成一圖形（簡稱曲邊扇形，右圖1），這里f（θ）在［α，β］上連續(xù)，且f（θ）≥0，求曲邊扇形的面積I.

圖1?曲邊扇形

解設(shè)I（θ）是由射線θ=α和角度為0的射線及f（τ）（τ∈［α，θ］）圍成的圖形的面積.

任取θ∈［α，β］，并取Δθ∈［0，β-α］，使θ+Δθ∈［α，β］，則在［θ，θ+Δθ］上的曲邊扇形是以角度為θ，θ+Δθ的射線及曲線r=f（τ）（τ∈［α，θ］）所圍成的平面圖形，其面積為ΔI，又因f（θ）在［α，β］上連續(xù)，所以分別存在最大值及最小值maxτ∈［θ，θ+Δθ］f（τ），minτ∈［θ，θ+Δθ］f（τ）.

∵ΔI≥Δθ2ππminτ∈［θ，θ+Δθ］?f2（τ）=12minτ∈［θ，θ+Δθ］?f2（τ）Δθ

ΔI≤Δθ2ππmaxτ∈［θ，θ+Δθ］?f2（τ）=12maxτ∈［θ，θ+Δθ］?f2（τ）Δθ

即?12minτ∈［θ，θ+Δθ］?f2（τ）Δθ≤ΔI≤12maxτ∈［θ，θ+Δθ］?f2（τ）Δθ

∴由判定法則1得：I=∫βα12?f2（θ）dθ.

8?微元分析法在物理中的應(yīng)用——變力對質(zhì)點的沖量［11］

例2：一個質(zhì)量為m的質(zhì)點在坐標oxy平面上運動，其在某一時刻t的位置矢量為r→=（acosωt，bsinωt）.求質(zhì)點A到質(zhì)點B的沖量I及外力做功W.

解在任一時刻t時，質(zhì)點速度：v→=dr→dt=（-ωasinωt，ωbcosωt），而其加速度為a→=dv→dt=-（ω2acosωt，ω2bsinωt）.

由牛頓第二定律，該質(zhì)點在任一刻t受到的力為：

F→=ma→=（F1，F(xiàn)2）=-（mω2acosωt，mω2bsinωt）.

在運動過程中小球在［t，t+Δt］上的沖量改變量為：ΔI=（ΔI1，ΔI2），則不難得到：

-mω2acosωtdt

-mω2bsinωtdt

故由判定法則2得：

I→=∫π2ω0F→dt=∫π2ω0（-mω2acosωt，-mω2bsinωt）dt=-mω（a，b）.

下再求外力做功，利用W=F→·S→=F→·v→t，并設(shè)在［t，t+dt］內(nèi)功函數(shù)改變量為ΔW，則：

m（-ω2acosω（t+Δt），-ω2bsinω（t+Δt））·（-ωasinω（t+Δt），ωbcosω（t+Δt）dt

m（-ω2acosωt，-ω2bsinωt）·（-ωasinωt，ωbcosωt）dt

從而再由判定法則1得：

W=∫π2ω0F→·v→dt

=∫π2ω0（-mω2acosωt，-mω2bsinωt）·

?（-ωasinωt，ωbcosωt）dt

=∫π2ω0（mω3a2sinωt-mω3a2sinωtcosωtdt

=mω22（a2-b2）

9?結(jié)論

定積分微元法是處理幾何、物理及經(jīng)濟應(yīng)用問題的一個理論基礎(chǔ)，以教育數(shù)學思路為導向，就曲邊扇形的面積和變力對質(zhì)點的沖量運用判定法則1和2分別進行了分析和計算，類似可考慮弧長、旋轉(zhuǎn)體體積、細棒質(zhì)量、變力做功、轉(zhuǎn)動慣量及經(jīng)濟問題。定積分微元分析法可以推廣為多元函數(shù)情形，對于重積分、線面積分的幾何、物理、經(jīng)濟應(yīng)用問題的分析與解決也是一個極好的借鑒。

致謝：非常感謝鄭州大學李夢如教授提供的相關(guān)參考文獻［1］［2］和［5］對本文的啟發(fā)以及審稿專家提出的寶貴意見。

參考文獻：

［1］韓云瑞，劉慶華.從教育數(shù)學看高等數(shù)學教材［J］.高等數(shù)學研究，2005，8（2）：3336.

［2］張景中.從數(shù)學難學談起［J］.世界科技研究與發(fā)展，1996（2）：2029.

［3］馬知恩，王綿森.工科數(shù)學分析［M］.高等教育出版社，2001.

［4］閆站立.微積分（第二版）［M］.高等教育出版社，2007.

［5］韓云瑞.微積分概念解析［M］.高等教育出版社，2007.

［6］同濟大學數(shù)學系.高等數(shù)學［M］.高等教育出版社，2007.

［7］吳贛昌.高等數(shù)學（理工類）［M］.中國人民大學出版社，2007.

［8］大學數(shù)學編寫委員會.高等數(shù)學［M］.科學出版社，2017.

［9］張?zhí)斓拢醅|.高等數(shù)學［M］.人民郵電出版社，2020.

［10］賀秋林.微元法原理探究［J］.工科數(shù)學，2001，17（3）：9596.

［11］黃生訓，楊紅.微元法在普通物理力學中的應(yīng)用［J］.中國科技信息，2006（08）：301302.

基金項目：國家自然科學基金（12101193）；河南省高等教育教學改革研究與實踐立項項目（2021SJGLX381）；2023年高等學校大學數(shù)學教學研究與發(fā)展中心項目“基于信息技術(shù)和學科交叉的高等數(shù)學課程教學創(chuàng)新與實踐”（項目編號：CMC20230205）；智慧教學背景下高等數(shù)學課程創(chuàng)新型數(shù)學體系的構(gòu)建與優(yōu)化設(shè)計研究（2023）

作者簡介：李靈曉（1976—?），女，碩士，教授，從事高等數(shù)學教學和非線性數(shù)學物理的研究。