AR 策略對強遮擋北斗監測站精度影響研究

許運習

（中國鐵路上海局集團有限公司合肥鐵路樞紐工程建設指揮部，安徽 合肥）

引言

自國內啟用北斗導航定位系統（Beidou Navigation Satellite System，BDS）以來，其在各行各業的影響已日益明顯。與其他導航系統相比，北斗因其抗遮擋特性、共視衛星數量及廣泛的信號頻段而在定位精度上有顯著優勢。在諸如鐵路、橋梁等基礎建設項目的變形監測中，北斗監測站憑借其全天候、低成本、高精度特點，已成為首選測量工具[1]。但遮擋環境中的多路徑效應對觀測精度有負面影響。傳統多路徑改正方法在大規模應用中面臨挑戰。為提高遮擋環境的定位精度，深入研究模糊度固定策略（Ambiguity Resolution，AR）是關鍵，其將助力更精確的殘差獲得，滿足監測工程需求。后續將基于RTKLIB 探討不同模糊度固定方法及其效益。

1 LAMBDA 搜索原理

在地面監測站的衛星觀測過程中，北斗系統普遍采用載波相位測量法。其中，特別關注的是B1 頻段信號，最為常用的載波信號頻率達到1 575.42 MHZ。該頻段的信號當中，相同的整周模糊度在載波相位信號中一直存在。為了實現精確的定位，確定載波相位的整周模糊度成為了首要任務。

核心的問題在于如何固定或確定這一模糊度。正因為此，GNSS 中的模糊度固定步驟被視為高精度定位的關鍵環節。而在多種嘗試和研究中，Teunissen 教授所提出的整數最小二乘模糊度降相關平差法（LAMBDA）脫穎而出，被認為是目前效果最佳的技術路徑[2-3]。

LAMBDA 的工作原理融合了整數降相關技術與最小二乘技術。其核心是在進行模糊度參數間的多維整數變換后，減少了相關性，為進一步的整數搜索創造了條件。之后，通過整數搜索完成固定，再將搜索結果轉化回模糊度的原始空間。不可忽視的是，本研究的核心工具RTKLIB，就選擇了LAMBDA 作為其主要的模糊度固定策略。

因為不同模糊度之間存在互相關聯，當一個模糊度參數發生變化時，會對其他模糊度的搜尋產生影響，從而增加搜索算法的復雜度。如果我們能夠減少模糊度參數間的關聯性，即一個模糊度的改變對其他模糊度的影響較小，那么可以有效地提高模糊度搜尋的速度。LAMBDA 算法是通過對模糊度參數及其方差- 協方差矩陣執行整數高斯轉換（也可稱作z 轉換），從原始空間轉移到新的空間，從而達到降低模糊度之間的相關性的目的[4-5]。

在此公式里，N、N0、QN是原始空間里的實數模糊度、整數模糊度和方差- 協方差矩陣。而、、QN則代表新空間里的實數模糊度、整數模糊度和方差- 協方差矩陣。其中的矩陣每個元素都是整數，且其行列式的絕對值為1；這一矩陣的逆也完全由整數構成，而z 包括眾多整數轉換的子矩陣。接下來，在新的空間進行模糊度的搜尋，得益于新空間中模糊度參數之間的相關性顯著下降，可以快速找到最優的模糊度組合。最終，將找到的精確模糊度組合通過逆轉換回到原始空間。

模糊度搜尋和先前提到的降相關是LAMBDA 算法中兩個互不相關的環節。即便不執行降相關步驟，我們依然能夠執行模糊度的搜尋。整數模糊度的搜索要求（目標方程f）為：

在這里，N 代表已給出的浮點模糊度數組；QN代表浮點模糊度的方差- 協方差矩陣其逆則為浮點模糊度的權重矩陣表示整數模糊度數組。通過在搜尋空間中尋找一個使得該公式達到最小值，從而確定模糊度。

2 AR 策略

為實現更為高效與準確的模糊度固定，RTKLIB集成了多種策略，主要包括：instantaneous、continuous以及fix-and-hold 三種模式[6]。

瞬時解算(Instantaneous)：此策略中，每個歷元都被視為一個全新的數據單元，不會受到其它歷元中模糊度估計結果的任何影響。這種策略特別適用于那些不連續或斷斷續續的數據，因為每個歷元的模糊度都是重新計算的，確保了其獨立性和準確性。

連續解算(Continuous)：與瞬時解算相對，連續解算策略會將當前歷元的模糊度浮點解作為后續歷元的初始值，從而確保解算的連續性。此策略的優點在于，能夠在多個歷元之間共享模糊度的信息，從而增加解算的穩定性和可靠性。

固定并持續(Fix-and-hold)：此策略進一步提高了模糊度解算的動態性。在固定解被確定后，它立即被用于調整和優化當前的模糊度浮點解。這種“實時融合”的策略有助于快速反應并適應不斷變化的測量環境和條件，從而提高整體解算的精確度。

總的來說，RTKLIB 提供的這三種策略均有其獨特的優勢，可以根據實際應用的需求和場景進行選擇和調整。

3 強遮擋北斗監測站實驗

為了探究不同模糊度確定策略對于在強遮擋條件下的北斗觀測站的定位精度所產生的效果，本部分選擇了某鐵路連續梁的一個參考站與一個觀測站進行科學實驗分析。圖1 描述的觀測站環境表明，觀測站所處的觀測條件較為惡劣，其四周被鐵制圍欄所阻隔，這對模糊度的確定產生了負面影響。

圖1 強遮擋北斗監測站

實驗所用數據是在2022 年5 月3 日至10 日這一段時間內采集的，相應地，年積日（Day-of-Year，DOY）為該年度的第123 天直至第130 天。數據記錄的時間間隔為1 秒，總的記錄周期為7*24 小時，且所選的高度截止角為15°。基準站和監測站都配備了HG-GCYH8372 型的天線和CRDC01 型號的接收設備。

在此項研究中，采用了第2 小節所述的三種RTKLIB 定位計算策略，分別為：瞬時解算策略（Instantaneous）、連續解算策略（Continuous）及固定并持續策略（Fix-and-hold），旨在深入探討北斗監測站的坐標數據系列。

圖2 中左上區域呈現了不同策略的固定率數據，以便更細致地揭示各坐標分量的波動特征，縱坐標詳細展示了NEU（北、東、上）各坐標分量。進而，右上區域顯示了各策略的標準偏差與均方根誤差，這二者均為關鍵的定位計算質量評估參數。標準偏差描述了數據的分散趨勢，而均方根誤差則闡述了預測與實際值的差距，為評定各計算策略性能提供了關鍵參考。此種多角度、多指標的評估方法有益于深度評析和對照三種策略處理北斗監測站數據的效果。

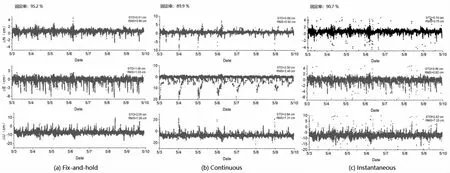
圖2 三種策略解算的坐標序列

根據圖2 的展示，三種解算策略：Fix-and-hold、Continuous 和Instantaneous 的固定率依次為95.2%、89.9%及90.7%。在此之中，Fix-and-hold 策略展現出了最高的固定率，隨后是Instantaneous，而Continuous策略的固定率最低。然而，從定位精度的角度考慮，平面方向上，Instantaneous 策略的標準偏差小于0.8 cm，顯示出最佳的定位精度。其次是Fix-and-hold 策略，其標準偏差小于1.0 cm，而Continuous 策略的定位精度最低，大約為2.3 cm。在高程方向上，這三種解算策略所展現的效果相似，大約在2～3 cm 之間。

再進一步觀察均方根誤差，可以明顯地發現，這三種策略在U 方向都呈現出約7 cm 左右的系統性偏差。這種偏差是由于多路徑效應導致的。值得注意的是，多路徑效應不僅在模糊度解算上產生了不利影響，其影響還會在高程分量中呈現，體現為高程的系統偏差。因此，在進行進一步的分析和解算時，應該充分考慮并糾正這部分誤差。

根據傳統的監測技術，當解算出坐標序列后，為了提高數據的穩定性與準確性，這些序列首先會經歷一個抗差處理過程，以消除或降低異常值的影響。接著，為了進一步優化數據質量，通常會采用濾波方法來減少噪聲或其它隨機干擾。在數據處理和優化后，為了方便后續分析，所得到的數據將會每隔1 小時進行一次平均，從而得到更為平穩的時序數據。最終，這些平均后的坐標值將與已知或真實的坐標進行比較，以評估解算坐標的準確性和可靠性。相關的圖形展示與詳細數據可以參考圖3 及表1。

表1 濾波處理后監測結果統計

圖3 濾波處理后監測結果

經詳細數據分析，可以得出以下觀察與結論：Instantaneous 策略在水平方向上展現出了卓越的定位精度，準確度達到了0.3 cm。相較之下，Fix-and-hold和Continuous 策略在同一方向的精度均為0.6 cm。對于高程方向的精度分析，Fix-and-hold 策略顯示為1.03 cm，Continuous 策略為1.15 cm，而Instantaneous策略為1.30 cm。這指出，在高程方向上，三者均未達到理想的精確度。進一步地，經過抗差處理并排除了明顯的粗差數據后，以及經過后續的濾波操作，依然可以觀察到E 方向和U 方向受多路徑效應影響的系統性偏差。更為具體地說，E 方向的系統偏差為0.7 cm，相對較小；而U 方向的偏差顯著，達到7 cm，幾乎是E 方向偏差的十倍。

綜上所述，考慮多路徑效應的顯著影響，尤其是在U 方向的高程測量上，使用這些監測站進行沉降觀測前，應當對多路徑效應進行仔細的修正與校準，以確保測量結果的準確性和可靠性。

4 結論

本文基于RTKLIB 深入分析了北斗監測站在強遮擋環境下的三種模糊度解算策略：Fix-and-hold、Continuous 和 Instantaneous。 研 究 結 果 表 明，Fix-and-hold 策略在模糊度固定率上達到95.2%，領先于Instantaneous 的90.7%和Continuous 的89.9%。在水平精度上，經過濾波處理后，Instantaneous 策略以0.3 cm 的精度表現最佳。而高程精度中，三者差異不大，但在未修正多路徑誤差前，均不適于沉降觀測。這些結論為北斗監測站在強遮擋環境中選擇模糊度解算策略提供了有力依據，并為后續研究提供參考。