基于多體動力學模型的柴油機曲軸振動特性分析

彭凌溥，柴子涵，金志浩

（沈陽化工大學 機械與動力工程學院，遼寧 沈陽）

引言

柴油機的曲軸系統的受力十分復雜，是由往復運動慣性力和燃燒壓力最大時的轉動慣性力以及曲軸系統的激振力等組成的。因此對曲軸系統的扭振分析是一個十分復雜的過程，過去一般建立一個等效離散系統模型，然后對模型在進行簡化分析，但是其中的誤差很大。建立一個和實體三維模型這樣就避免了簡化所產生的誤差，而且動力學仿真更加直觀的計算出實際的激振力。發動機曲軸系統的激振力會引發曲軸扭振，會通過動力傳輸路線傳遞給其他構件。以上所提到的就是該多體動力學仿真方法與其他計算方法相比的優點。

Zeischka[1]使用了曲軸和發動機缸體的多體彈性動力學模型，模型使用了有限元模型，隨后被導入整體四缸發動機模型，包括連桿和活塞的剛體表示。流體動力學軸頸效應通過阻抗方法實現。阻抗圖提供了軸頸力與軸承尺寸、油粘度和偏心率等參數的函數關系。

郭一鳴[2]提出了一個詳細的單缸內燃機多體數值非線性動力學模型。該模型結合了發動機部件的大位移動力學、支撐軸承的無限小振動和截留空氣力燃料氣缸瞬態壓力的同步求解。獲得的結果提供了所有慣性構件（如活塞、飛輪和連桿）的動態響應的時間歷程，還獲得了曲軸的扭轉振動以及軸頸軸承的同步和異步旋轉。

戴成[3]討論了如何將多體動力學與柔性體效應相結合，以預測軸承載荷、曲軸振動、每個軸頸的軌跡圖以及由于結構柔性而產生的軸承性能。滑動軸承中的油膜效應采用阻抗法和流體動力油膜結合有限元法來實現。以一臺V6 發動機為例，說明了柔性系統和滑動軸承載荷的動態響應。

楊鑫[4]提出了一個4 缸4 沖程柴油發動機的多體模型，結合了部件的靈活性。該模型還包括發動機點火順序和實驗測量的燃燒時間歷程，以提供由于柔性曲軸系統的組合扭轉- 偏轉模式引起的飛輪錐形運動的數值預測，這種振動響應的數值預測與實驗結果符合得很好。

現代仿真方法是以實體模型為基礎，利用柴油機示能圖加載激磁力矩，并考慮曲軸軸承支承力、軸系與機體的耦合作用，使柴油機曲軸系統扭振計算接近實際工況，有利于獲得準確的計算結果。本文采用UG建立了某型重型柴油機曲軸系統的三維模型，該系統由曲軸、活塞、連桿、飛輪和硅油阻尼器組成。并利用ADAMS 建立剛柔耦合的軸系多體動力學模型，將柴油機曲軸轉化為柔性體。曲軸的輕微變形可以保證具有變形廣義坐標一階項的動力學方程的完整精度。

1 曲軸系統裝配模型

根據某型重型汽車柴油機軸系零件及裝配圖，建立由曲軸、活塞、連桿、曲柄銷、飛輪、硅油阻尼器等模型零件組成的曲軸系統，運用三維建模軟件UG，然后組裝起來如圖1 所示。

圖1 柴油機軸系動力學模型

由于飛輪的質量和轉動慣量很大，相對于測功機和柴油機而言。柴油機臺架試驗采用柔性連接，限制了扭振對曲軸系統的影響。因此在動力響應分析仿真中，剛柔混合多體系統不考慮測功機和彈性聯軸器部件。基于上述模型求解系統的動態響應，得到系統動態響應的時程，計算分析系統的扭振響應。

1.1 曲軸系統動力學模型

用UG 將曲軸系統模型裝配完成后導入ADAMS,然后建立約束模型如圖1 所示。

硅油阻尼器造型：外殼與曲軸之間建立固定連接，慣性塊與外殼之間增加旋轉連接，慣性塊與外殼之間增加扭簧連接。

1.2 曲軸多體動力學模型

在軟件ADAMS/Auto Flex 模塊中先在曲軸表面劃分大小為10 mm 的網格，然后用“Find Attachments”將曲軸周圍的連接點找出來連接附近的節點。

自動構建曲軸柔性體替代原有剛體，并在連接點施加約束力。我們可以在柔性曲軸特性中查看曲軸的各個振動模態，前1-6 模態頻率很小，接近于零，可以舍棄。前十自由模態的柔性曲軸如圖2 所示。

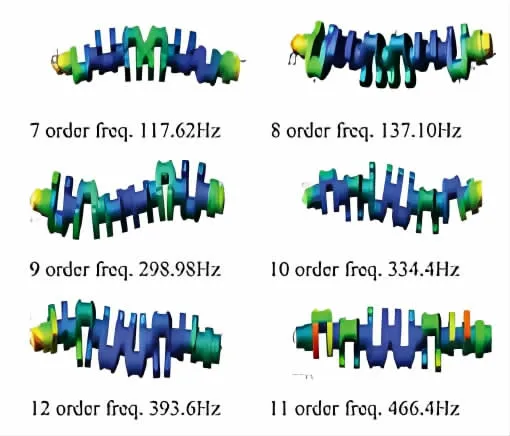
圖2 ADAMS 剛柔耦合柴油機軸系多體模型圖

1.3 硅油阻尼器動態模型

硅油阻尼器主要通過阻尼部分（慣性塊）和驅動部分（外殼）來實現減振，其機械模型簡圖可簡化為圖3。

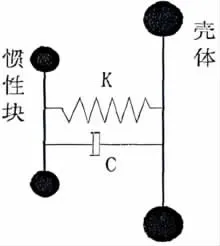
圖3 硅油阻尼器的機械模型

將硅油視為純粘性流體，僅表現阻尼作用，彈性系數k=0，用工作過程動平衡法計算各轉速對應的阻尼器系數。

2 柴油機軸系主要負荷

2.1 柴油機示功圖

通過柴油機臺架試驗，按圖4 所示外特性曲線施加負載，測量各轉速點（800、900、1 000、1 100、1 200、1 300、1 400、1 500、1 600、1 700）的轉速對應的指示圖(曲軸轉角1 度時各缸氣壓)如圖5 所示為轉速為1 900 rpm。

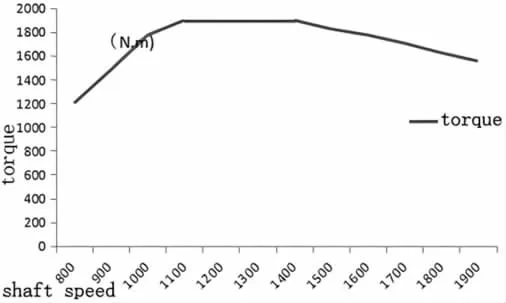
圖4 柴油機外特性曲線

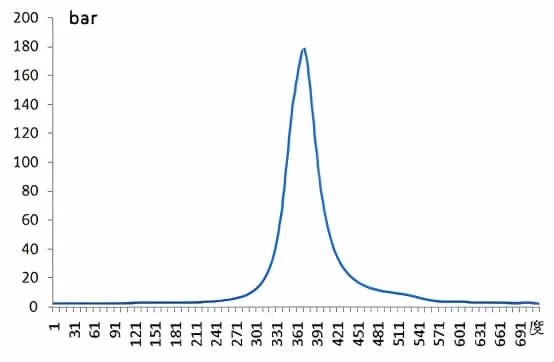
圖5 柴油機轉速（1 900 r/min）示功圖

2.2 施加軸系載荷

氣缸內壓力與活塞端面積的乘積得到活塞上的載荷。6 缸負荷大小基本相同，只是各缸峰值時間不一樣，由ADAMS 中的函數AKISPL 插值法得到壓力。6缸頂部承受的載荷力如圖6 所示。

3 仿真結果

該柴油機工作轉速范圍為800～2 100 r/min，計算轉速區間為100 r/min，模擬了曲軸系統的扭振，提取了曲軸自由端的瞬時轉速信號數據。首先減去平均速度得到瞬時速度差，然后是扭振得到曲軸系統自由端的響應（扭角），進行FFT，得到扭角幅值。

選取1 700 r/min 轉速、3 000 步/秒下的仿真數據，通過該仿真得到曲軸自由端（硅油阻尼器安裝在曲軸上）的瞬時轉速和扭矩，數據曲線如圖7～9 所示。

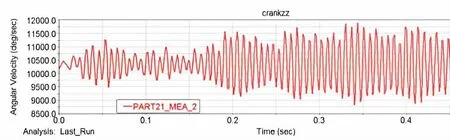
圖7 曲軸自由端的瞬態角速度圖

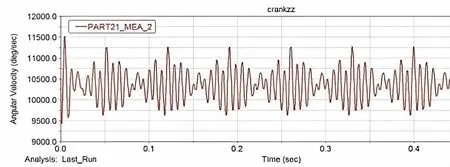
圖8 自由端瞬態角速度與平均角速度的差異圖

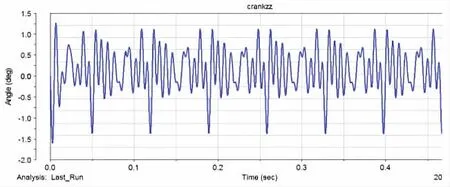
圖9 瞬態曲軸自由端角的積分圖

當轉速為1 700 r/min 時，6 次諧波頻率為170 Hz。從圖10 得出曲軸自由端的扭轉角為156 度。對于本文分析的6 缸柴油機，可能引起曲軸危險共振的發動機干擾轉矩為3、4、6 次諧波。其中，6 次諧波的扭振幅值最大。

圖10 曲軸自由端扭轉振動角值的頻譜圖

該柴油機800～2 100 r/min、各轉速間隔100 r/min 的仿真結果采用相同的方法進行計算，根據曲軸對應的轉速，曲軸自由端6 次諧波扭轉角的幅值將系統提取出來，繪制出曲軸系統自由端的6次諧波扭矩- 轉角曲線，如圖11 所示。曲軸系統自由端扭轉角的最大幅度為0.16 度，共振速度約為1 800 轉/分。

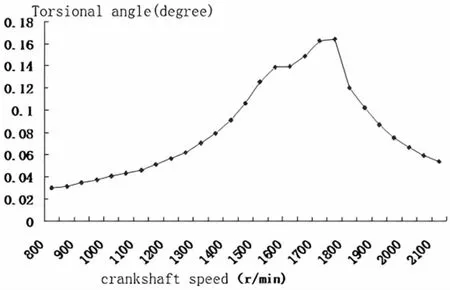
圖11 軸系統自由端的扭轉角

4 結論

利用多體動力學研究了曲軸系統扭轉振動研究的一般方法和步驟。通過ADAMS 對純粘性硅油阻尼器冪律流體的力學模型和多體動力學模型進行仿真分析。

得出的結論有：當柴油機裝上與之相應的硅油阻尼器運行時，軸系扭振明顯減小，主諧波最大扭轉角(6 次諧波）從0.54 降低到0.16，阻尼效果非常明顯。

通過多體動力學仿真得到軸系的扭振幅值和共振轉速，與實際試驗結果接近，仿真計算具有較高的精度和應用價值。