溫度-軌道不平順組合激勵下車-軌-橋耦合動力響應分析

李鵬鑫，邢書科，王兆剛，郭玉鵬，楊宇栓，楊榮山

(1.西南交通大學高速鐵路線路工程教育部重點實驗室,成都 610031; 2.中鐵上海工程局集團有限公司,上海 201906; 3.山東省路橋集團有限公司,濟南 250101; 4.山東鐵路投資控股集團有限公司,濟南 250101)

1 概況

某多跨矮塔混凝土斜拉橋位于艾山至濼口水文站間的黃河河段,年極端氣溫為-19.7～42.7 ℃。雙線鐵路,無砟軌道,設計速度350 km/h,為我國第一條在千米級的長聯矮塔混凝土斜拉橋上鋪設無砟軌道的高速鐵路。

大橋主體結構為五塔雙索面形式,采用塔墩固結、半漂浮體系,跨徑布置為6跨5塔(108+4×216+108) m,主橋橋跨布置如圖1所示。主梁截面形式選用單箱雙室斜腹板箱形變截面(圖2),高7.015 m,寬13.8 m,腹板斜率為1∶15;主塔為H形斜橋塔,塔高38 m;斜拉索采用半扇形布置,單個索塔設8對拉索,主塔處索間距為1.2 m,主梁處索間距為8.0 m。

圖1 主橋立面布置(單位:cm)Fig.1 Main bridge elevation arrangement (unit: cm)

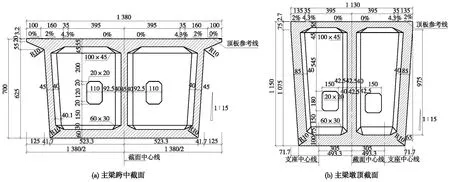
圖2 主梁截面(單位:cm)Fig.2 Main beam section (unit: cm)

千米級的矮塔斜拉橋跨度較大,且鋪設精度較高的無砟軌道對外荷載作用較為敏感,溫度荷載作用下橋梁結構極易產生較大變形,影響列車運行的平穩性及安全性[1-3]。目前關于大跨度橋上鋪設無砟軌道研究已取得了一定成果,魏周春[4]建立車橋耦合振動模型,分析了橋梁預拱度與軌道不平順共同作用對車橋動力響應的影響;李永樂等[5-7]建立風-車-橋系統空間耦合動力學模型及橋系統節段模型風洞試驗,研究了風-車-橋的耦合振動性能;王彪[8]構建車-橋耦合振動模型,研究了曲線半徑、外軌超高及緩和曲線長度對車橋耦合動力作用影響,并給出了相應的取值范圍;國巍[9]利用OpenSees與Simpack軟件進行聯合仿真,對強地震作用下橋上高速行車的安全性進行了分析。

由上述文獻可知,外部激勵荷載對橋上無砟軌道行車的動力分析主要集中在風載、地震、橋梁預拱度、曲線半徑以及外部超高。對于大跨度混凝土斜拉橋,由于結構自身的剛柔特性,溫度作用引起橋梁結構的幾何變形將對橋上列車的高速行駛帶來不利影響。考慮溫度變化引起橋梁的幾何變形對上部無砟軌道結構的影響,對列車高速過橋時車-軌-橋耦合系統的動力響應進行了計算分析,研究了溫度引起的橋梁變形與軌道不平順的組合不平順激勵下,車-軌-橋耦合系統動力響應的變化規律及特點。

2 車-軌-橋耦合系統

2.1 橋梁-軌道系統有限元模型

根據矮塔斜拉橋及橋上無砟軌道的結構特點和受力特征,建立橋梁-軌道系統精細化空間有限元模型(圖3),其中支座和緩沖墊層采用三向線性彈簧單元模擬,扣件采用非線性彈簧模擬,各結構材料參數見表1。由于梁端布設鋼軌伸縮調節器,鋼軌做斷軌處理,對溫度變化引起的主橋上軌道長波不平順無影響,因此,不考慮引橋及引橋上部軌道結構的模型建立。

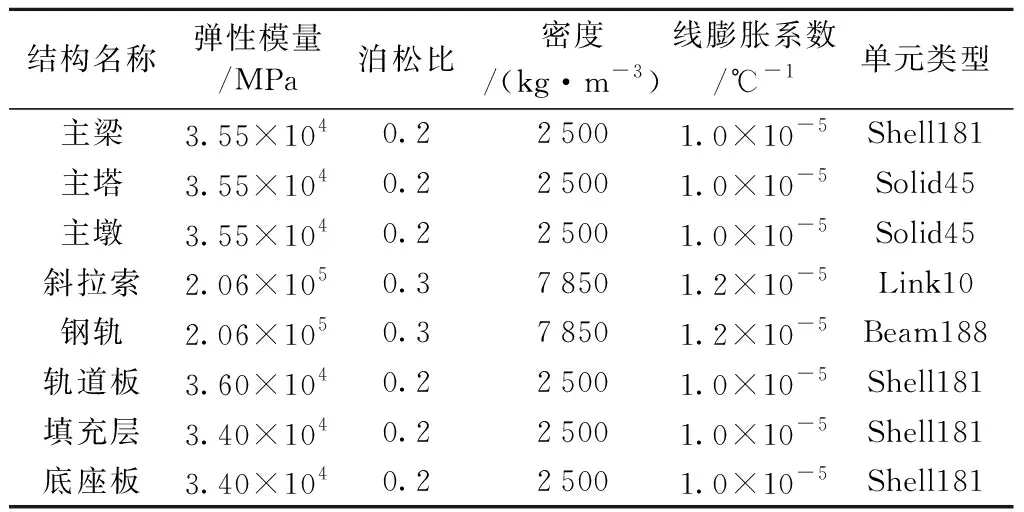
表1 各結構材料參數Table 1 Individual structural material parameters

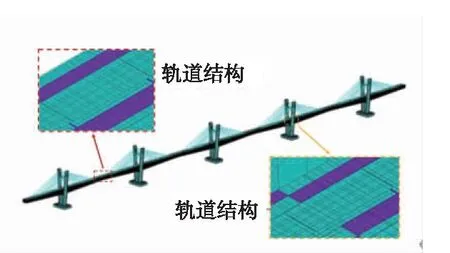
圖3 橋梁-軌道系統有限元模型Fig.3 Finite element modeling of bridge-track system

2.2 車-軌-橋模型

列車選用CRH2C列車,動車組采用8節編組,單節列車車輛模型主要由1個車體、2個轉向架、4個輪對共7個剛體組成,其中輪對和轉向架通過一系懸掛連接,車體和轉向架通過二系懸掛連接。

將橋梁劃分為主梁、斜拉索、墩塔、支座、輔助墩五類子結構,軌道劃分為底座板、軌道板兩類子結構,利用Bushing力元連接各子結構,組成軌道-橋梁多層柔性整體系統,將車輛模型作為外部子結構導入軌道-橋梁系統,將車輛與下部多層柔性體整體系統進行連接,車-軌-橋系統耦合動力學分析模型如圖4所示[10-15]。

圖4 車-軌-橋系統耦合動學力分析模型Fig.4 Vehicle-rail-bridge system coupling dynamic force analysis model

3 溫度-軌道不平順激勵組合

3.1 荷載取值

對于全年氣溫變化引起的橋梁及上部無砟軌道結構的升降溫,其特點是變化緩慢,給橋梁-軌道系統帶來的是結構內部平均溫度的變化,因此,根據該橋所在地區的氣溫統計資料,得出橋梁-軌道系統計算模型的基礎溫度取15 ℃,系統升溫取+30 ℃,降溫取-35 ℃。斜拉索與主梁、墩、塔等混凝土結構溫差取±10 ℃,墩、塔橫向溫差取+5 ℃;主梁截面的溫度非線性變化分布按式(1)、式(2)計算,箱梁沿板厚溫差按照式(3)、式(4)計算。根據橋址的地理位置和氣候條件,取梁高方向溫差為20 ℃,梁寬方向溫差為10 ℃;軌道結構垂向溫度梯度按式(1)進行計算,與主梁混凝土結構的垂向溫差取+5 ℃;溫度負效應倍數取0.5[16]。

Ty=T01e-ay

(1)

Tx=T02e-ax

(2)

(3)

(4)

式中,Tx、Ty分別為主梁截面某一點在x,y方向上的溫差;T01、T02分別為梁高、梁寬方向的溫差;δ為板厚;a、a′為日溫差計算指數。

鎖定軌溫按式(5)進行計算。設計鎖定軌溫鎖定范圍取±5 ℃,其中鋼軌最大升溫按當地最高鋼軌溫度與設計鎖定軌溫限之差計算[16]。

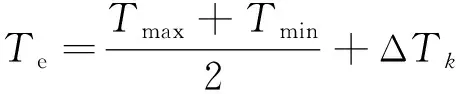
(5)

式中,Tmax為當地年最大溫度;Tmin為當地年最小溫度;ΔTk為設計鎖定軌溫修正值,可取0～5 ℃。

綜上,對橋梁-軌道系統整體溫變、系統及內部溫差進行組合,考慮溫度效應引起橋梁-軌道系統幾何形變的最不利情況,可得兩種溫度荷載組合,一是系統整體升溫+正溫差組合,簡稱為“升溫組合工況”;二是系統整體降溫+負溫差組合,簡稱為“降溫組合工況”,見表2。

表2 溫度荷載工況Table 2 Temperature loading condition

3.2 系統整體升溫+正溫差組合

系統整體升溫+正溫差組合鋼軌變形如圖5所示,鋼軌與主梁協同變形,在鋼軌豎向變形方面,左、右兩軌變形規律一致,幅值相近,其上拱變形最大值約為20.340 mm,下撓變形最大值約為26.910 mm;鋼軌橫向變形范圍為-4.69～8.38 mm;從全橋跨度來看,在系統整體升溫+正溫度梯度荷載作用下,鋼軌線型在豎、橫兩個方向仍基本呈直線線型。

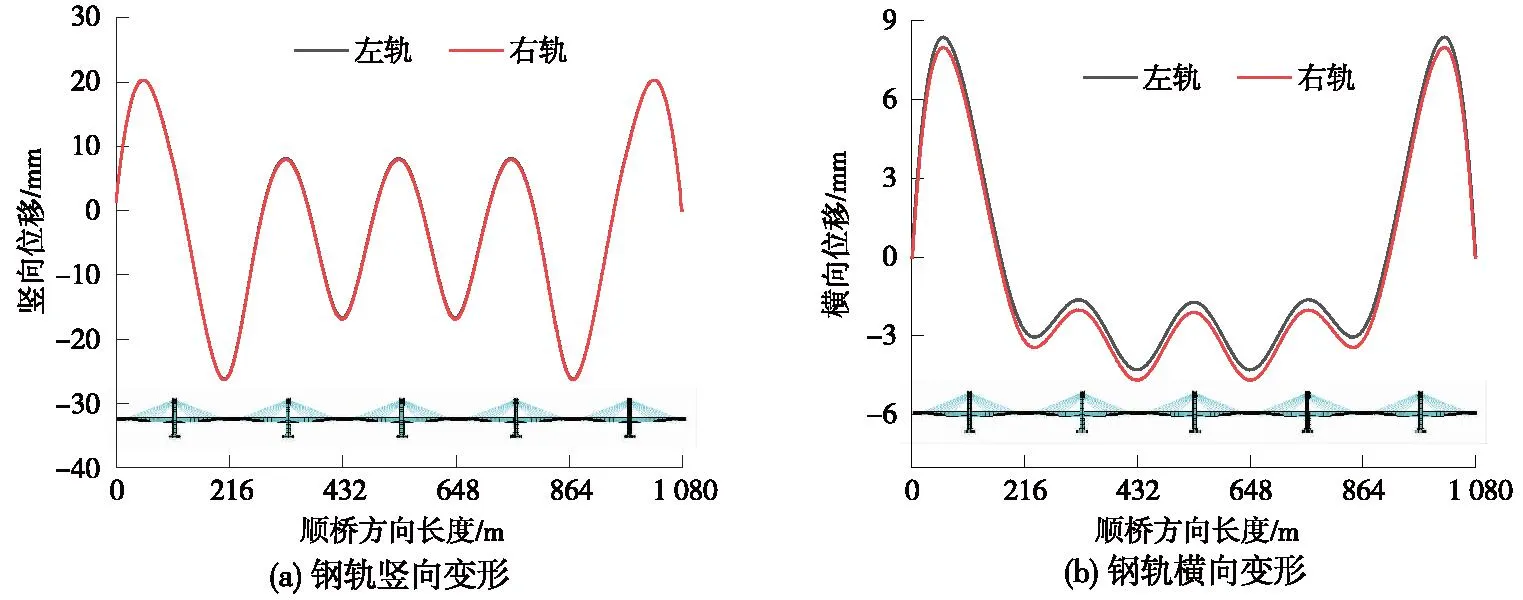
圖5 系統整體升溫+正溫差組合鋼軌變形Fig.5 System overall warming+positive temperature difference combination rail deformation

3.3 系統整體降溫+負溫差組合

系統整體降溫+負溫差組合鋼軌變形如圖6所示,鋼軌與主梁同樣具有良好的協同變形關系,且變形趨勢與升溫組合工況相反,在鋼軌豎向變形方面,左、右兩軌變形一致,幅值接近,其上拱變形最大值為17.1 mm,下撓變形最大值為13.22 mm;鋼軌橫向變形范圍為-5.19～1.23 mm,在系統整體降溫+負溫度梯度荷載作用下,鋼軌線型在豎、橫兩個方向仍基本呈直線狀態。

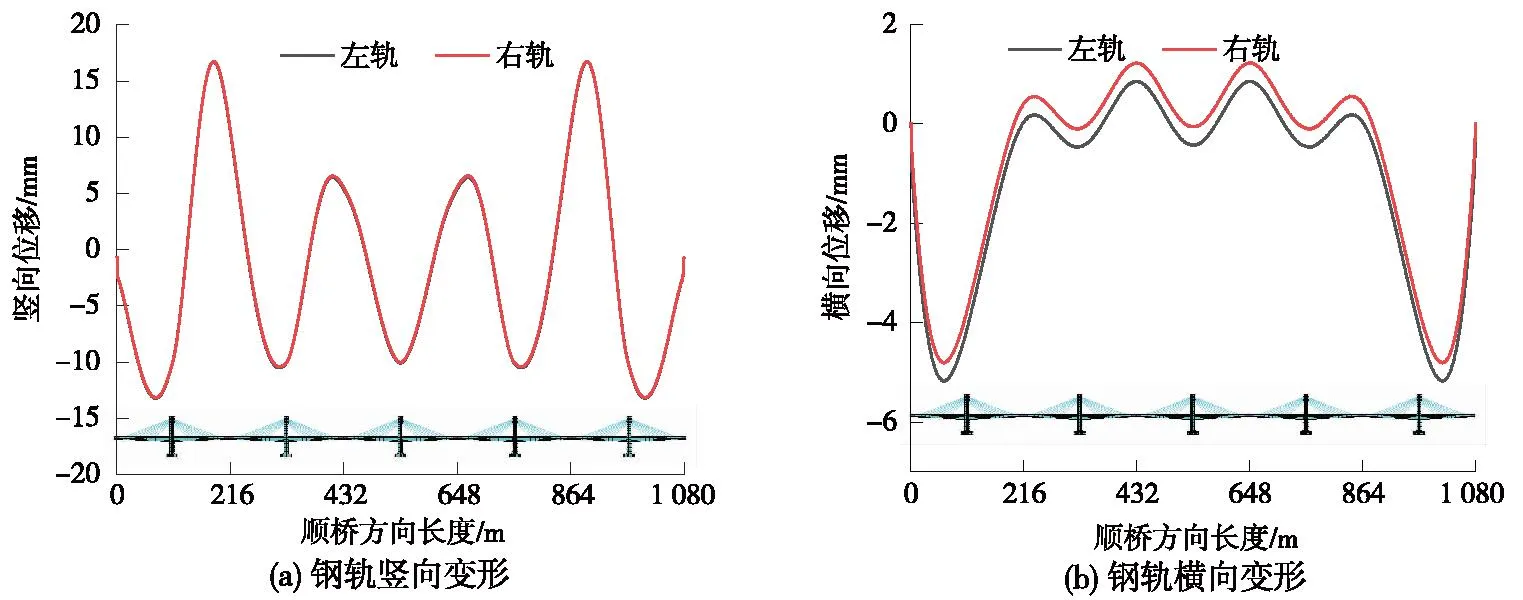
圖6 系統整體降溫+負溫差組合鋼軌變形Fig.6 System overall cooling+negative temperature difference combination rail deformation

3.4 溫度不平順與軌道不平順組合

對比升溫及降溫兩種組合工況下橋梁-軌道系統的位移變形結果,相較于降溫組合工況,升溫組合工況下橋梁整體變形范圍更大,這是系統整體升溫溫差大于降溫溫差的緣故,而在此工況下,鋼軌的豎、橫向變形幅值及橫向變形之差波動范圍則更小,這主要是考慮溫度梯度荷載時,負溫度梯度荷載需取0.5的折減系數[17]。

基于中國高速鐵路譜和升溫組合工況下橋梁及橋上軌道結構的最不利變形結果,將二者反映在左、右兩股鋼軌在高低、軌向兩個方向上的形變位移進行疊加,得到溫度作用引起橋梁的長波不平順與中國高速鐵路譜疊加之后的橋上線路組合不平順,如圖7所示。

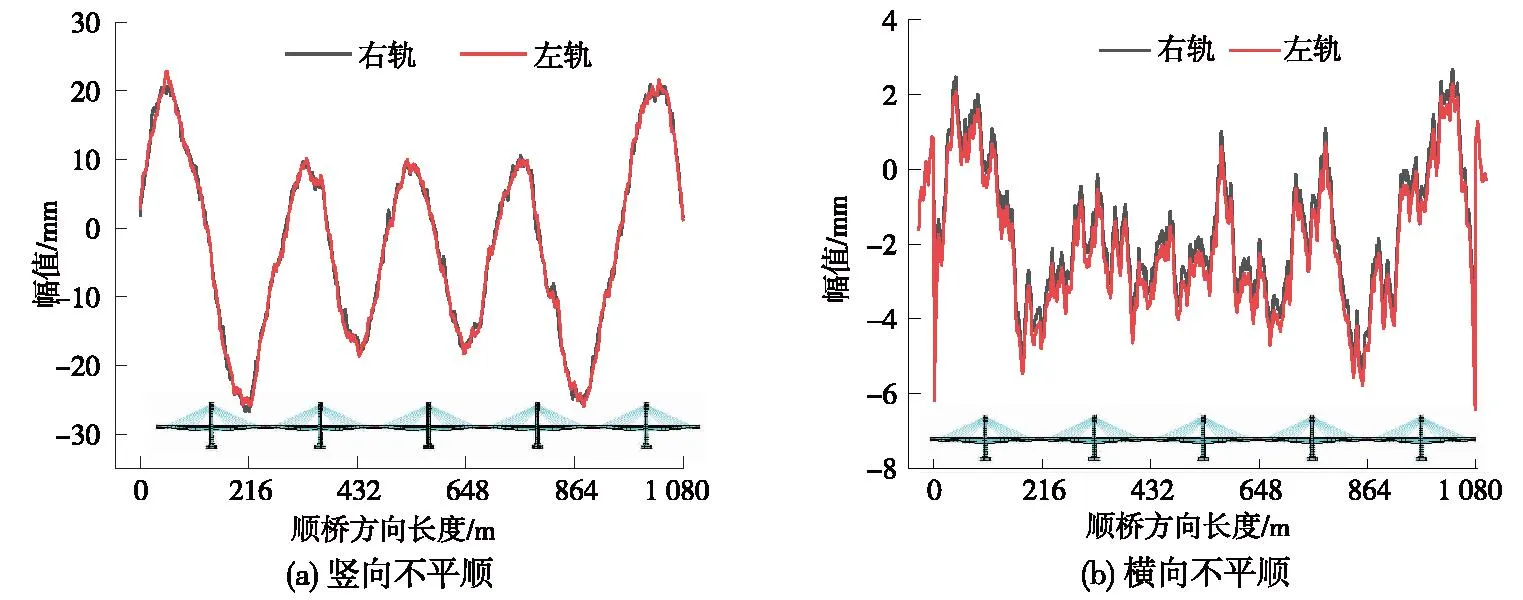
圖7 線路組合不平順Fig.7 Line combinations are not smooth

4 組合不平順下車-橋動力響應分析

4.1 車輛動力響應

行車速度為350 km/h時,車體的垂、橫向加速度,輪軌垂、橫向力,脫軌系數以及輪重減載率時程曲線分別見圖8～圖10。

圖8 車體加速度Fig.8 Vehicle body acceleration

由圖8可知,動車垂向加速度最大值為0.8 m/s2,拖車垂向加速度最大值為0.66 m/s2,均小于車體的垂向加速度指標限值1.28 m/s2;動車橫向加速度最大值為0.59 m/s2,拖車橫向加速度最大值為0.56 m/s2,均小于車體的橫向加速度指標限值0.98 m/s2。動車垂、橫向Sperling指標分別為2.34和2.17,拖車垂、橫向Sperling指標分別為2.22和2.14,均達到“優秀”等級,滿足行車舒適性要求。在列車過橋整個時段,動車的垂、橫向加速度及Sperling指標普遍大于拖車的垂、橫向加速度,這與動車的軸重相對較大存在一定關系。

由圖9、圖10可知,從列車運行安全性來看,在全橋各跨跨中位置車輛各動力響應較為強烈,且動車各動力響應略大于拖車各動力響應,其時差規律明顯。動車、拖車輪軌最大垂向力分別為111.65,109.72 kN,動車、拖車輪軌最大橫向力分別為10.06,8.08 kN,均小于各響應指標限值;動車脫軌系數最大值為0.12,拖車脫軌系數最大值為0.09,動車、拖車的輪重減載率最大值分別為0.44、0.41,滿足行車安全性相關要求[18-21]。

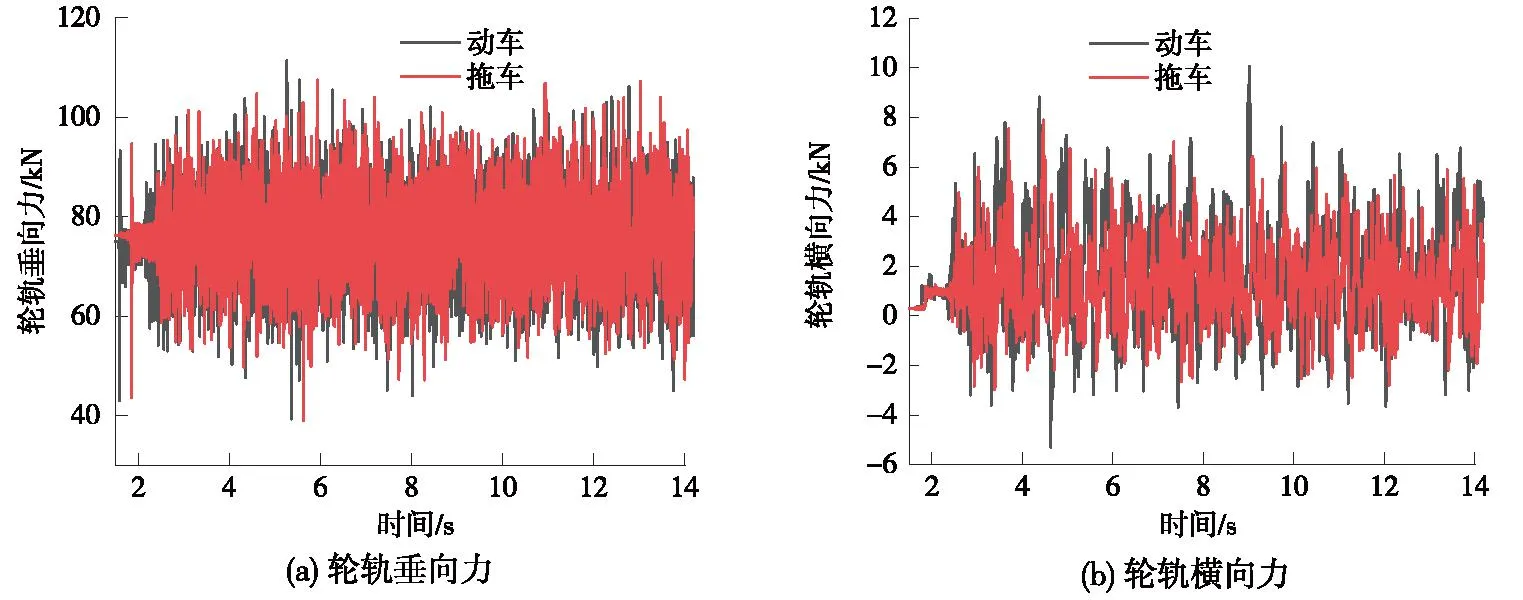
圖9 輪軌力Fig.9 Track force

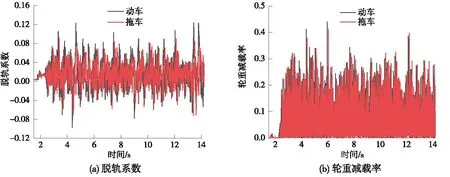
圖10 車輛安全性指標Fig.10 Vehicle safety indicators

4.2 行車速度對車-橋耦合系統動力性能的影響

以250,300,350,400 km/h的行車速度為設計工況(其中400 km/h為檢算行車速度),對不同行車速度下車-橋耦合系統動力響應的指標符合情況及變化規律進行探討。各行車速度下車輛動力學響應最值見圖11～圖14。

圖11 行車速度對車體加速度的影響Fig.11 The effect of travel speed on vehicle body acceleration

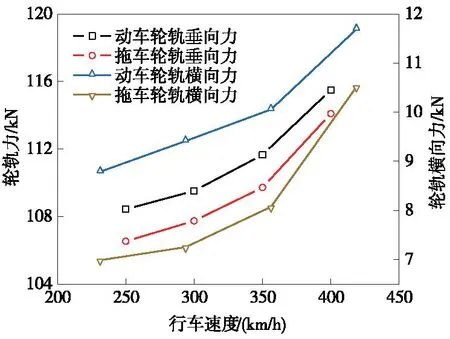
圖12 行車速度對輪軌力的影響Fig.12 The effect of travel speed on track force

圖13 行車速度對安全系數的影響Fig.13 The effect of travel speed on safety coefficient

圖14 Sperling舒適度Fig.14 Sperling comfort

在車輛舒適性評價方面,車體的垂、橫向加速度最值及對應舒適度指標與行車速度呈正相關變化趨勢,且增幅隨行車速度增加而不斷增大。在行車速度達到400 km/h時,車體豎向Sperling舒適性指標評價由“優秀”轉為“良好”;車體垂向加速度最大值達到0.95 m/s2。但總體來講,400 km/h的驗算行車速度能夠通過車輛各舒適性方面規范要求,而在350 km/h的設計行車速度下,車輛各舒適性動力響應整體都處于較優水平,列車過橋時的行車舒適性較好。

在車輛安全性評價方面,輪軌的垂向及橫向力、脫軌系數、輪重減載率最值隨行車速度的增加而增大,且增幅同樣與行車速度呈正比例關系,相較于其他行車速度區間,在350～400 km/h的行車速度區間,各車輛安全性動力響應最值增幅顯著提升。在各車輛安全性動力響應中,僅輪重減載率接近規范限值,行車速度為400 km/h時,輪重減載率最大值取0.45,未達到限值。因此,在設計行車速度350 km/h及檢算行車速度400 km/h的條件下,車輛各安全性動力響應均符合各響應指標規定,列車過橋時行車安全性可靠[18-21]。

提取前述各行車速度下橋梁各結構動力學響應最值,其分布曲線見圖15～圖18。由變化趨勢看,橋梁各動力響應最值與行車速度同樣呈正相關變化趨勢,尤其在行車速度為350～400 km/h區間內,主梁及塔頂處各動力響應指標增幅顯著,列車速度增加會加劇橋梁的振動。

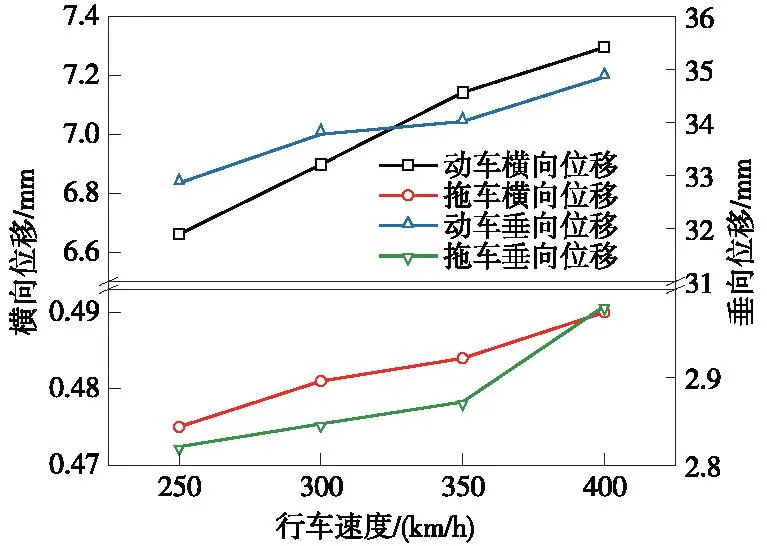
圖15 主梁位移Fig.15 Displacement of main girder

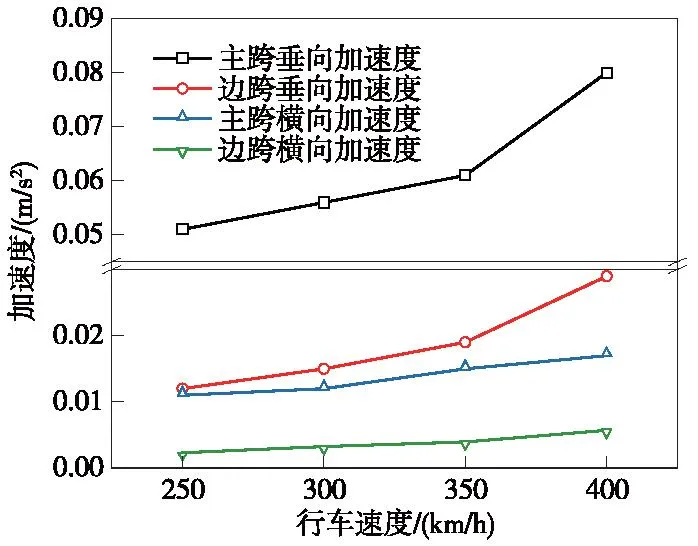
圖16 主梁加速度Fig.16 Acceleration of main girder

圖17 墩、塔位移Fig.17 Displacement of piers and towers

圖18 墩、塔加速度Fig.18 Acceleration of piers and towers

由各動力響應指標限值看,在位移變形方面,在行車速度為400 km/h條件下,墩頂最大橫向位移為1.94 mm,接近但仍小于指標限值。在加速度方面,橋梁各動力響應最值均遠小于規范限值。整體來看,在上述工況下,橋梁各動力響應主要以位移變形為控制變量,400 km/h的驗算行車速度能夠通過橋梁各動力響應相關規范要求,而列車在以350 km/h的設計行車速度過橋時,橋梁動力性能良好[18-21]。

5 結論

基于車-軌-橋系統動力學模型,針對主梁為箱梁的千米級長聯矮塔混凝土斜拉橋,討論分析了溫度-軌道不平順組合激勵下橋上無砟軌道的車輛動力響應,主要結論如下。

(1)千米級長聯矮塔混凝土斜拉橋上無砟軌道在溫度-軌道不平順組合激勵下,以350 km/h設計行車速度過橋時,動車垂向加速度最大值為0.8 m/s2,動車橫向加速度最大值為0.59 m/s2,輪軌最大垂向力為111.65 kN,滿足相關規范要求。

(2)車體的加速度最值與行車速度呈正相關趨勢,在行車速度達到400 km/h時,車體垂向加速度最大值達到0.95 m/s2,墩頂最大橫向位移為1.94 mm,均滿足相關規范要求;動車、拖車的Sperling舒適度均超過限值2.5,Sperling舒適性指標由“優秀”轉為“良好”,行車舒適度相對較差。