車輪多邊形磨耗對車橋耦合振動響應的影響

唐德發，吳夢雪，徐昕宇，張鈔奕，李永樂

(1.西南石油大學土木工程與測繪學院,成都 610500; 2.中鐵二院工程集團有限責任公司,成都 610031; 3.西南交通大學土木工程學院,成都 610031)

引言

車輪多邊形磨耗也叫做車輪諧波磨耗,是車輪踏面在圓周方向出現的波形磨耗,廣泛存在于鐵路運輸現場[1-4],但目前對其形成機理尚缺乏統一認識。車輪多邊形磨耗會使系統產生高頻振動以及更大的輪軌沖擊力。這種高頻振動可能造成車輛和軌道零部件的損壞,還會通過軌道傳遞至橋梁結構,對橋梁結構的疲勞性能造成影響。而輪軌沖擊力的增大以及車輪多邊形磨耗引起的滾動噪聲將會嚴重降低列車行駛安全性和旅客乘坐舒適性。因此,車輪多邊形磨耗研究一直受到學者們的廣泛關注。

在車輪多邊形磨耗成因方面,趙曉男等[5-6]研究發現,輪軌間蠕滑力飽和引起的摩擦自激振動、列車制動滑動易引發車輪多邊形磨耗;金學松等[7-8]詳細研究了高速列車車輪多邊形磨耗的形成機理、影響和控制措施;康熙等[9]根據現場測試和多體動力學仿真結果研究了高速列車車輪偏心磨耗的形成機理與發展規律。在車輪多邊形磨耗對列車動力響應的影響方面,羅仁等[10]考慮輪對的彎曲變形,研究了車輪多邊形磨耗對車輛系統動力學性能的影響,發現車輪多邊形磨耗使輪軌垂向力顯著增大,但對列車運行的平穩性影響不大;張潔娟等[11]通過分析車輪多邊形磨耗對某高速動車組動力學性能的影響規律發現,車輪多邊形磨耗對列車垂向振動響應的影響更為顯著;吳磊等[12]通過建立直線電機列車-軌道耦合動力學模型,分析了不同磨耗程度車輪對輪軌法向力和脫軌系數的影響;王憶佳等[13]采用車輪圓周輪廓法建立了車輪多邊形磨耗模型,計算了高速運營狀態下周期性車輪多邊形磨耗對車輛動力學性能的影響,以輪軌垂向力為指標劃定了車輪多邊形磨耗的安全區域;WU等[14-15]和胡曉依等[16-17]的研究表明,與剛性輪軌相比,柔性輪軌加速了車輪多邊形磨耗的發展,使列車-軌道耦合系統產生更大的振動響應;劉歡[18]利用SIMPACK建立了列車-軌道的剛柔耦合動力學模型,研究了典型車輪多邊形磨耗階次、幅值和運行速度對輪軌力和振動響應的影響。在車輪多邊形磨耗噪聲影響方面,韓鐵禮等[19]通過跟蹤測試車輪多邊形發展和轉向架區域振動噪聲,研究了車輪多邊形磨耗對列車轉向架區域噪聲的影響規律。

上述對車輪多邊形磨耗的形成機理、對列車動力響應影響規律等研究均針對列車-軌道耦合系統,還未有文獻在車橋耦合系統中考慮車輪多邊形磨耗的影響。此外,在上述研究中有部分未考慮軌道不平順的作用,這與列車實際的運營狀態不符。當列車以一定速度通過橋梁時,列車質量沿橋跨的移動會改變橋梁結構的自振特性,由于軌道不平順、機車車輛質量的不完全對中、各部件制造的不準確以及輪軌缺陷等因素,運動的車輛、軌道、橋梁會發生耦合振動[20]。而車輪多邊形磨耗所產生的振動可能使橋梁的振動更加劇烈,而橋梁振動又反過來對車輛和軌道結構的振動產生影響,使橋上列車運行的安全性、平穩性以及橋梁結構運營的安全性進一步惡化。因此,對車輪多邊形磨耗作用下車橋耦合振動的規律展開研究,為保障橋上列車的安全、平穩運行以及橋梁結構的安全運營提供參考。

1 車橋耦合動力學模型

1.1 列車多體動力學模型

基于多體動力學理論,以國內某高速列車拖車車輛為原型,運用專業的多體動力學分析軟件SIMPACK建立了相應的多體動力學模型。模型中車體、轉向架、輪對、軸箱等均考慮為剛體。列車的一、二系減振器采用彈簧阻尼元件進行模擬,并考慮了減振器的非線性特性。列車主要參數如表1所示。

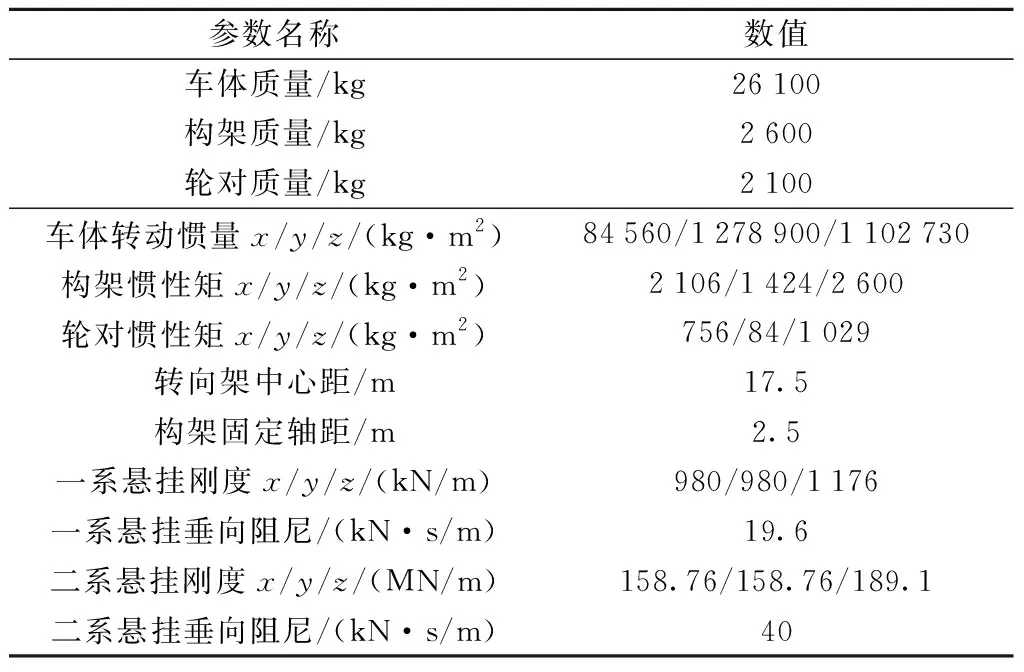
表1 列車模型主要參數Table 1 Main parameters of train model

1.2 橋梁、軌道有限元模型

用有限元分析軟件ANSYS分別建立文獻[21]中國內某高速鐵路單跨32 m雙線簡支梁橋和CHN60型鋼軌的有限元模型,單元類型均采用Beam188單元。考慮列車在橋梁左線行駛。軌道為CRTSⅠ型雙塊式無砟軌道,假定軌道板與橋梁連接牢靠,不對軌道結構振動做貢獻,將道床板視為橋梁的參振質量,按二期恒載施加于主梁上。具體截面和材料參數分別如圖1和表2所示。

圖1 箱梁截面(單位:mm)Fig.1 Box girder section(unit: mm)

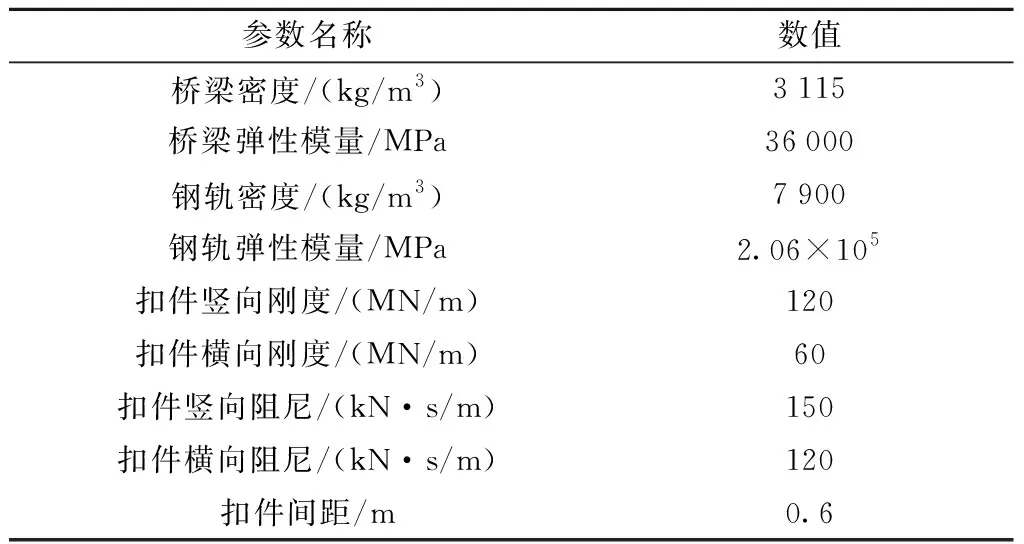
表2 橋梁、鋼軌和扣件主要參數Table 2 Main parameters of bridge, rail and fastener

多體動力學分析軟件SIMPACK與有限元軟件聯合仿真主要通過讀取有限元模型的質量、剛度、阻尼以及模態矩陣實現,并通過模態綜合法計算有限元模型的動力響應[22]。采用Guyan模態縮減法對橋梁有限元模型進行子結構分析,生成SIMPACK能識別的結果文件,在不影響計算精度的情況下,盡量縮減模型的自由度。ANSYS得到的橋梁模態和橋梁導入SIMPACK后的模態對比如表3所示,限于篇幅,本文僅給出了3階車輪多邊形磨耗對應頻率附近的高階模態來驗證ANSYS模態縮減結果的正確性,其中簡支梁橋主梁和橋墩的橫向彎曲模態如圖2所示。

圖2 主梁和橋墩的橫向彎曲Fig.2 Lateral bending of main girder and piers

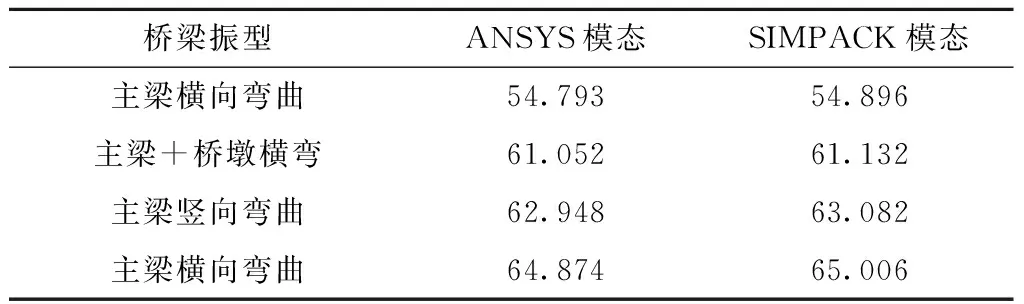
表3 高階模態信息對比 HzTable 3 Comparison of high-order modal information

從表3可以發現,ANSYS模態分析結果與導入SIMPACK后的橋梁模態誤差最大不超過0.25%,即自由度縮減后的模型不會影響計算精度,表明橋梁有限元模型的主自由度選擇合理。

1.3 車橋耦合模型

建立車橋耦合模型的關鍵是實現列車和橋梁作用力的耦合。利用SIMPACK自帶的柔性軌道模塊,實現列車和鋼軌之間作用力的耦合,進一步完成輪軌接觸設置,從而建立列車-鋼軌耦合模型。其中輪軌法向力采用Hertz理論計算,蠕滑力則采用FASTSIM算法求得。然后,通過彈簧阻尼力元模擬鋼軌扣件實現鋼軌和簡支梁橋的連接,而橋墩和地面的連接則用大剛度彈簧模擬固結約束。為驗證本文模型建立方法的正確性,以車速250 km/h過橋為例,對比了ANSYS靜力過橋瞬態分析與SIMPACK車橋耦合振動分析時橋梁跨中豎向最大位移,結果如表4所示。

表4 計算結果對比Table 4 Comparison of calculation results

由表4可知,ANSYS靜力過橋瞬態分析與SIMPACK車橋耦合振動分析的計算結果吻合較好,證明了本文中模型建立方法的正確性。車橋耦合模型如圖3所示。

圖3 車橋耦合模型Fig.3 Rail vehicle-bridge coupling model

2 車橋耦合系統的輸入激勵及其影響規律

2.1 車輪多邊形磨耗

車輪多邊形磨耗是車輪圓周在不均勻磨耗等因素作用下形成的周期性輪徑偏差,可由式(1)的傅里葉級數形式表示[3]。

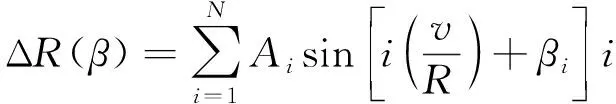
(1)

式中,ΔR(β)為輪徑偏差;Ai為第i階車輪多邊形幅值;βi為第i階車輪多邊形初始相位角。

理想的列車車輪即使剛經過鏇修或在鏇修后較短的運行里程內,都有可能被檢測出初始多邊形磨耗[7]。1階車輪多邊形磨耗是由車輪安裝或加工造成的偏心,3階車輪多邊形磨耗是由制造過程中三角爪固定方式造成的三角化,2階和4階車輪多邊形磨耗分別表示車輪的橢圓化和四邊化[13]。這種初始車輪多邊形磨耗會隨著列車運行里程增加而發展。而初始低階車輪磨耗產生的振動頻率相對較低,更加接近簡支梁橋的振動頻率,將會對車橋耦合系統的振動產生更大的影響。因此,本文主要探究低階的初始車輪多邊形磨耗對車橋耦合系統的影響規律。車輪多邊形磨耗在SIMPACK中用非恒定半徑的車輪進行模擬,即車輪的公稱半徑隨車輪旋轉角度而變化,通過Untrueness模塊完成設置。圖4展示了1～4階車輪多邊形磨耗的極坐標示意。

圖4 車輪多邊形磨耗示意Fig.4 Diagram of polygon wear of wheels

2.2 軌道不平順

軌道不平順是由于在鐵路線路的平直段,鋼軌并不是呈理想的平直狀態,兩根鋼軌在高低和左右方向相對于理想的平直軌道存在偏差,這種幾何參數的偏差即為軌道不平順。我國高速鐵路總體技術條件建議對列車進行平穩性分析時使用德國高速線路軌道譜。因此,本文的軌道不平順譜選用適用于高速鐵路線路的德國低干擾譜,采用三角級數法對高低不平順、方向不平順和水平不平順的不平順序列進行模擬,原理如式(2)所示。

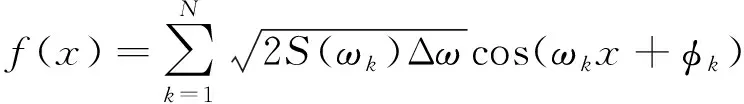
(2)

式中,f(x)為模擬得到的軌道不平順序列;S(ωk)為功率譜密度函數;ωk為軌道不平順的空間頻率;φk為第k個頻率的相位,是獨立均布于0～2π的隨機數。

由三角級數法模擬得到的垂向軌道不平順功率譜密度與德國低干擾譜吻合較好,如圖5所示。

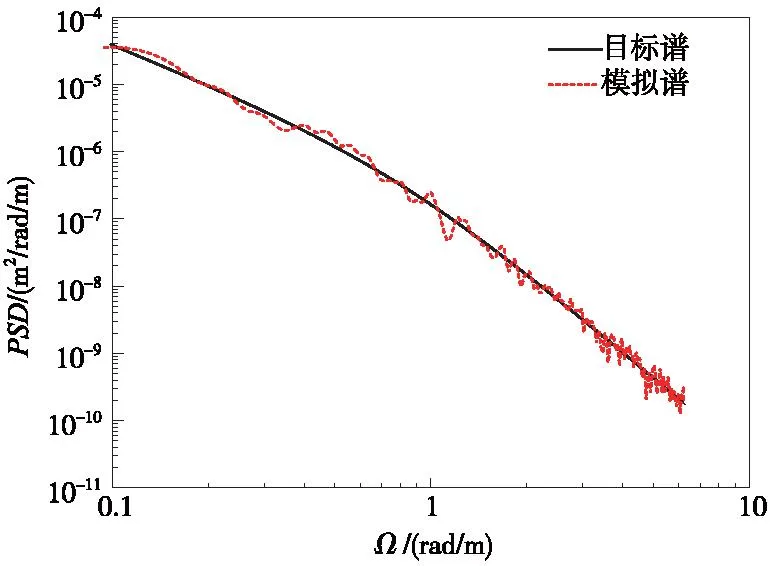
圖5 模擬譜與目標譜垂向不平順對比Fig.5 Vertical irregularity comparison of simulated spectrum with target spectrum

2.3 不同輸入激勵對耦合系統振動響應的影響

為分析車輪多邊形磨耗對車橋耦合系統的影響,對比了僅以軌道不平順作為輸入激勵時和同時把軌道不平順和車輪多邊形磨耗(階數為3階,幅值為0.04 mm)作為輸入激勵時耦合系統動力響應的差異。列車的平穩性指標、橋梁跨中和鋼軌中點的豎向位移如分別圖6、圖7所示,其中鋼軌中點是指橋梁跨中位置處對應的鋼軌節點,后文的鋼軌測點均為該位置。

圖6 列車平穩性指標對比Fig.6 Comparison of train stability index

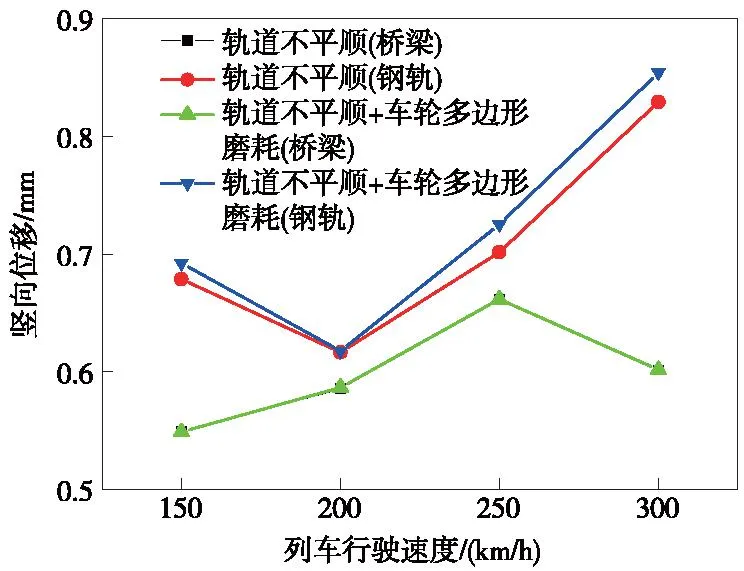
圖7 橋梁跨中和鋼軌中點豎向位移Fig.7 Vertical displacements at mid-span of bridge and rail

由圖6可知,車輪多邊形磨耗對列車運行的平穩性幾乎無影響,這是因為車輪多邊形磨耗的頻率一般較高,超出了列車平穩性指標敏感范圍,與文獻[10]和文獻[13]結果一致。由圖7可知,橋梁跨中和鋼軌中點的豎向位移隨列車運行速度的提升總體呈現上升趨勢但并非單調遞增,車輪多邊形磨耗對橋梁跨中豎向位移幾乎無影響,但會使鋼軌中點豎向位移略微增大。

列車以200 km/h速度運行時,不同輸入激勵作用下列車的輪重減載率、橋梁跨中和鋼軌中點的振動加速度分別如圖8～圖12所示。

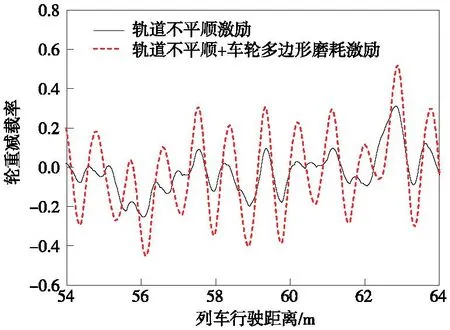
圖8 輪重減載率對比Fig.8 Comparison of the wheel unloading rate

圖9 橋梁跨中橫向加速度響應對比Fig.9 Comparison of lateral acceleration response at mid-span of bridge

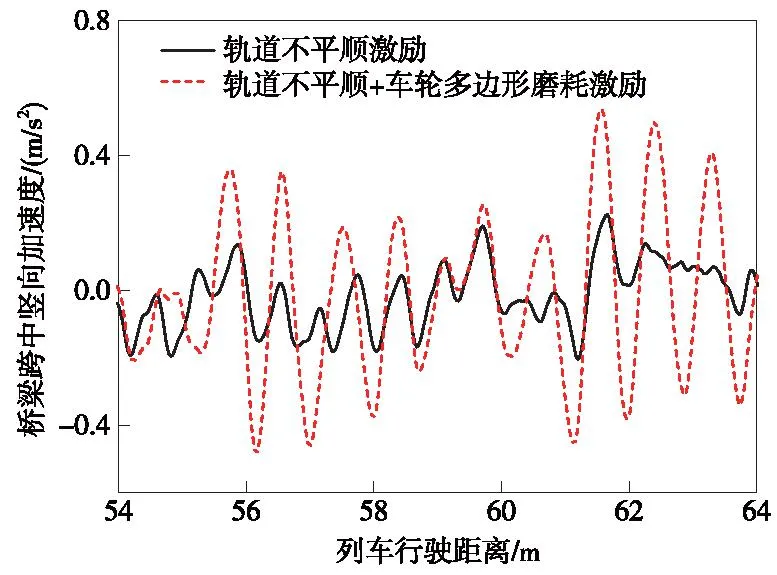
圖10 橋梁跨中豎向加速度響應對比Fig.10 Comparison of vertical acceleration response at mid-span of bridge

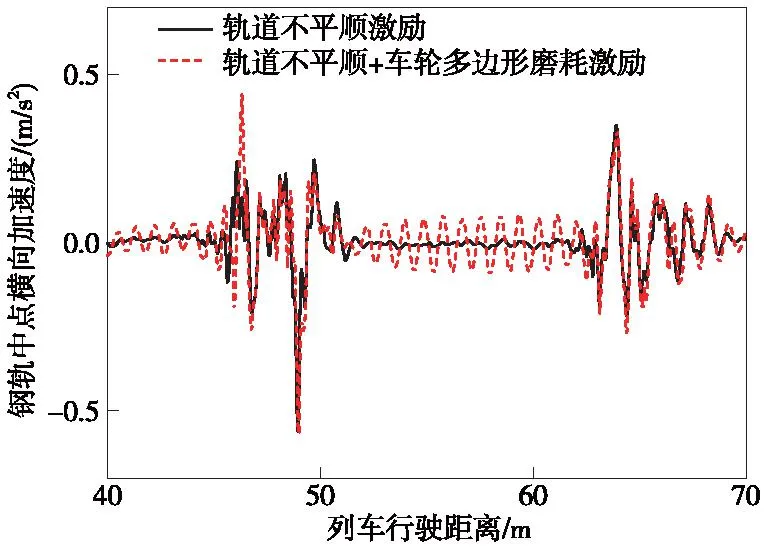
圖11 鋼軌中點橫向加速度響應對比Fig.11 Comparison of lateral acceleration responce at mid-span of rail

圖12 鋼軌中點豎向加速度響應對比Fig.12 Comparison of vertical acceleration responce at mid-span of rail

由圖8～圖12可知,輪重減載率在僅具有軌道不平順時的最大值為0.31,而有車輪多邊形磨耗共同作用時的最大值為0.52。相對于僅具有軌道不平順作用時的工況,車輪多邊形磨耗使得列車的輪重減載率最大值增大了67.7%,這將降低列車運行的安全性。有車輪多邊形磨耗共同作用時,橋梁跨中的橫向和豎向振動加速度最大值分別為僅具有軌道不平順作用時的2.74倍和2.27倍,橋梁的振動加速度顯著增大。車輪多邊形磨耗還使鋼軌中點的橫向和豎向振動加速度最大值相對于僅具有軌道不平順作用時分別增大了26.4%和85.4%。由圖12可以發現,鋼軌中點的豎向加速度由于車輪達到時間的不同存在4個明顯的峰值。綜上所述,車輪多邊形磨耗對車橋耦合系統的振動響應影響顯著,針對車輪多邊形磨耗對車橋耦合系統振動響應的影響規律展開研究是十分有必要的。

3 車輪多邊形磨耗對車橋耦合系統的影響規律研究

軌道不平順激勵是隨機的,這也使得車橋耦合系統的動力響應是典型的隨機過程。隨機軌道不平順即使疊加了車輪多邊形磨耗,車橋耦合系統動力響應的計算結果也僅是隨機過程的一次實現,只代表車橋系統隨機響應的某一個樣本。為詳細探究車輪多邊形磨耗對車橋耦合系統的影響規律,對比分析了不同階數、幅值的車輪多邊形磨耗和相同軌道不平順共同作用下,車橋耦合系統的列車輪重減載率、橋梁跨中和鋼軌中點的橫向和豎向振動加速度等指標的變化規律。

3.1 車輪多邊形磨耗幅值的影響

為探究車輪多邊形磨耗幅值對車橋耦合系統振動響應的影響規律,設定列車運行速度為200 km/h,車輪多邊形磨耗階數為3階、幅值為0.02～0.08 mm,得到的耦合系統振動響應結果如圖13～圖17所示。

圖13 不同幅值磨耗作用下列車輪重減載率響應Fig.13 Wheel unloading rate response with different amplitudes of polygon wear of wheels

圖14 不同幅值磨耗作用下橋梁跨中橫向加速度響應Fig.14 Lateral acceleration responce at mid-span of bridge with different amplitudes of polygon wear of wheels

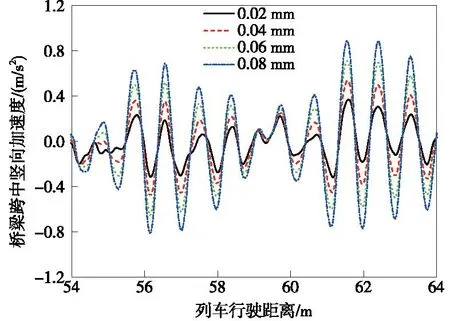
圖15 不同幅值磨耗作用下橋梁跨中豎向加速度響應Fig.15 Vertical acceleration responce at mid-span of bridge with different amplitudes of polygon wear of wheels

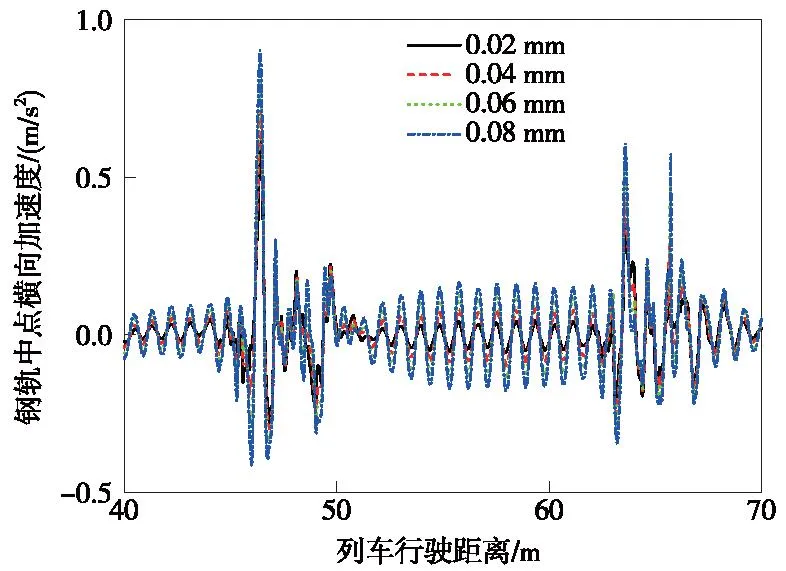
圖16 不同幅值磨耗作用下鋼軌中點橫向加速度響應Fig.16 Lateral acceleration responce at mid-span of rail with different amplitudes of polygon wear of wheels

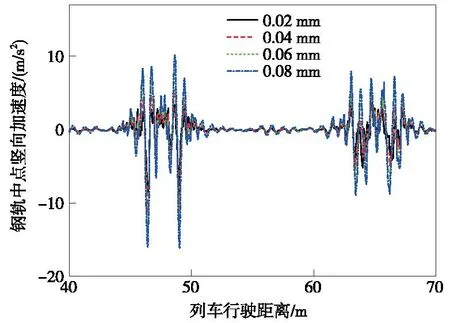
圖17 不同幅值磨耗作用下鋼軌中點豎向加速度響應Fig.17 Vertical acceleration responce at mid-span of rail with different amplitudes of polygon wear of wheels

由圖13～圖17可知,隨著車輪多邊形磨耗幅值增大,列車輪重減載率、橋梁跨中和鋼軌中點的振動加速度增大;車輪多邊形磨耗幅值由0.02 mm增大至0.08 mm,使列車的輪重減載率增大了76.5%,鋼軌中點的橫向和豎向加速度最大值分別增大了47.3%和83.1%;而車輪多邊形磨耗幅值為0.08 mm時,橋梁跨中的橫向和豎向加速度最大值是幅值為0.02 mm時的2.76倍和2.42倍。隨著列車運營里程增加,車輪多邊形磨耗的幅值也將隨之增加,這將使得車橋耦合系統的振動更加劇烈,甚至可能會威脅到行車安全。

3.2 車輪多邊形磨耗階數的影響

為探究車輪多邊形磨耗階數對車橋耦合系統的影響,把1～4階車輪多邊形磨耗和軌道不平順作為系統的輸入激勵,列車運行速度為200 km/h,車輪多邊形磨耗幅值為0.04 mm。列車輪重減載率、橋梁跨中和鋼軌中點的橫向和豎向振動加速度分別如圖18～圖22所示。

圖18 不同階數磨耗作用下列車輪重減載率響應Fig.18 Wheel unloading rate responce with different orders of polygon wear of wheels

由圖18～圖22可知,隨著車輪多邊形磨耗階數增加,列車輪重減載率、橋梁跨中和鋼軌中點的振動加速度均隨之增大。4階車輪多邊形磨耗作用時,列車輪重減載率最大值、橋梁跨中豎向加速度最大值、鋼軌中點的橫向和豎向加速度最大值分別為1階車輪多邊形磨耗作用時的2.16倍、4.89倍、1.82倍和2.7倍。特別地,由圖19可知,3階車輪多邊形磨耗作用下橋梁跨中的橫向加速度增大顯著,甚至遠大于4階車輪多邊形磨耗作用下的振動響應。對3階車輪多邊形磨耗作用下的輪軌作用力和橋梁跨中橫向加速度響應進行頻域分析,結果如圖23和圖24所示。

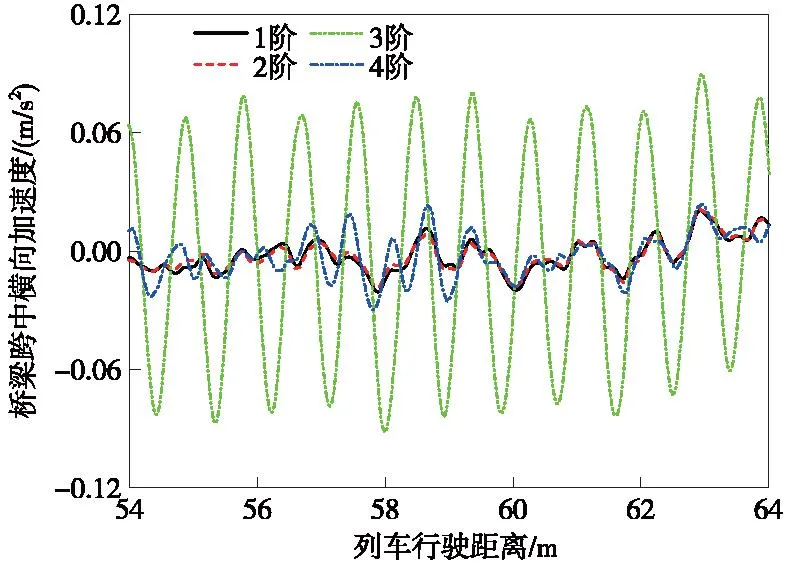
圖19 不同階數磨耗作用下橋梁跨中橫向加速度響應Fig.19 Lateral acceleration responce at mid-span of bridge with different orders of polygon wear of wheels

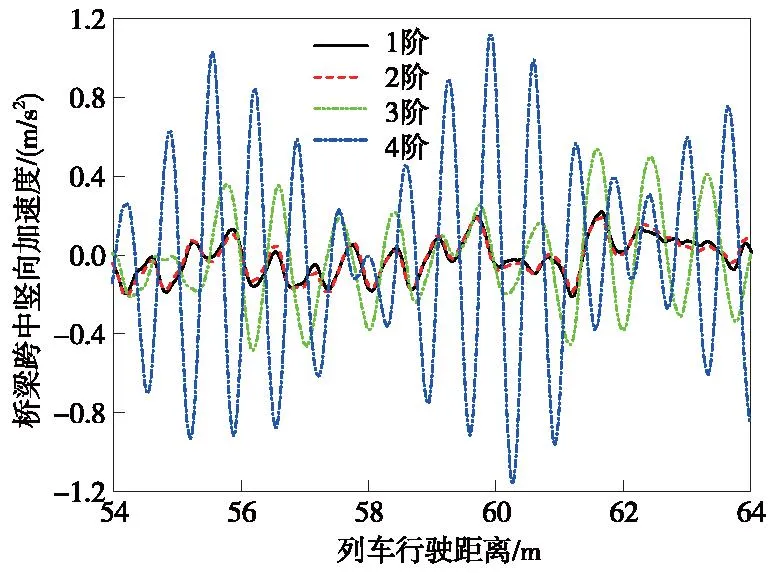
圖20 不同階數磨耗作用下橋梁跨中豎向加速度響應Fig.20 Vertical acceleration responce at mid-span of bridge with different orders of polygon wear of wheels

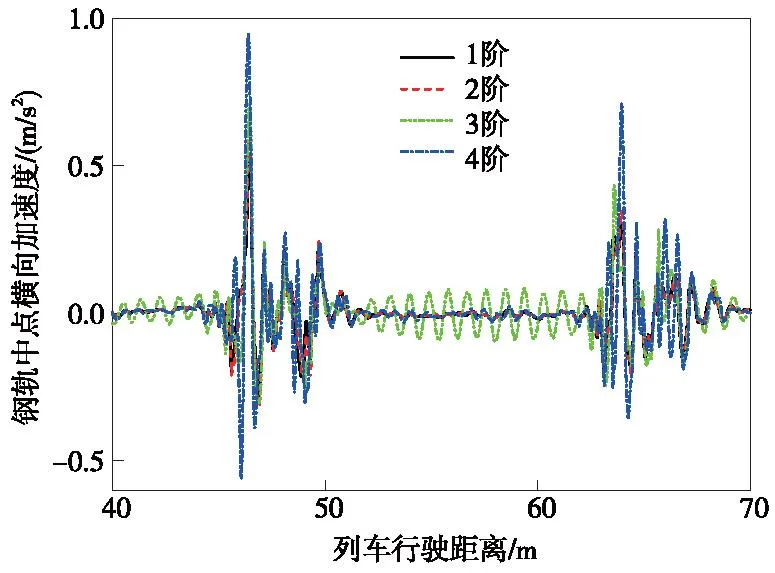
圖21 不同階數磨耗作用下鋼軌中點橫向加速度響應Fig.21 Lateral acceleration responce at mid-span of rail with different orders of polygon wear of wheels

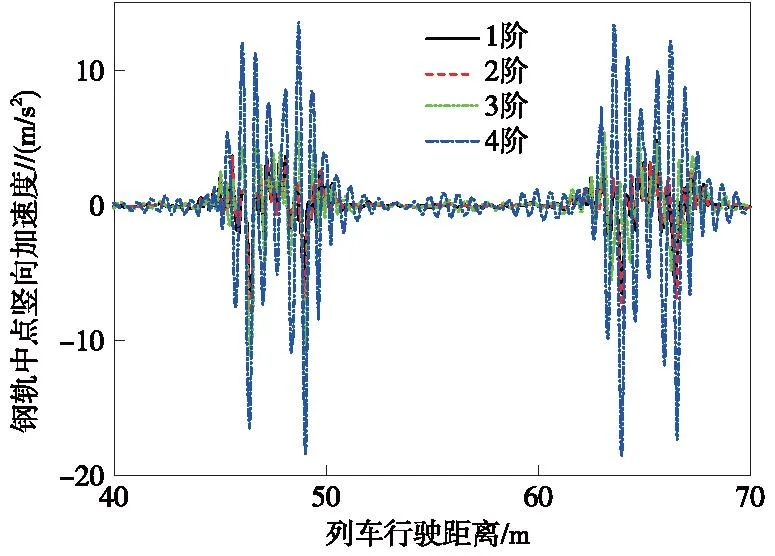
圖22 不同階數磨耗作用下鋼軌中點豎向加速度響應Fig.22 Vertical accelerations at mid-span of rail with different orders of polygon wear of wheels

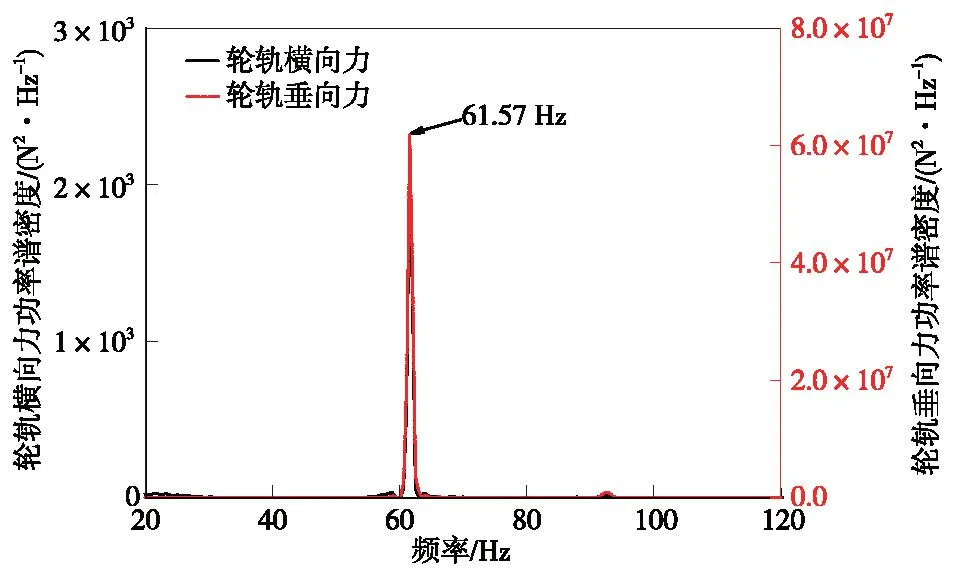
圖23 輪軌作用力頻域分析結果Fig.23 Frequency domain analysis results of wheel-rail force

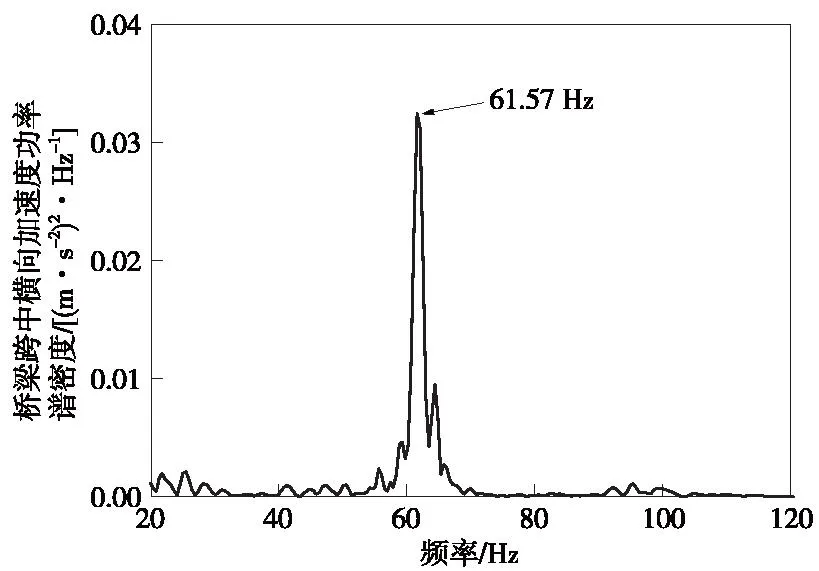
圖24 橋梁跨中橫向加速度頻域分析結果Fig.24 Frequency domain analysis results of lateral accelerations at mid-span of bridge

由圖23和圖24可知,3階車輪多邊形磨耗引發的列車輪軌作用力頻率為61.57 Hz,和橋梁跨中橫向加速度響應的峰值頻率相同。而該簡支梁橋在61Hz頻率附近存在橫向振動模態(表3和圖2)。因此,可以認為3階車輪多邊形磨耗引發的橋梁振動頻率和橋梁的橫向自振頻率相近,從而引發橋梁橫向共振,使得橋梁橫向加速度顯著增大。綜上所述,高階車輪多邊形磨耗引起的車橋耦合振動響應更大,但某些階數的車輪多邊形磨耗可能引發橋梁共振使得橋梁的振動響應顯著放大,可能對車橋耦合系統安全性和結構耐久性造成影響。

4 結論

為探究車輪多邊形磨耗對車橋耦合振動響應的影響規律,為保障具有車輪多邊形磨耗的高速列車安全運營提供參考。首先,基于ANSYS和SIMPACK聯合仿真的方法建立了車橋耦合模型;然后,以不同輸入激勵研究了車輪多邊形磨耗對耦合系統的影響程度;最后,探究了不同幅值、階數的車輪多邊形磨耗和軌道不平順共同作用時車橋耦合系統振動響應的影響規律,得出如下結論。

(1)車輪多邊形磨耗對車橋耦合系統的振動響應影響顯著。3階車輪多邊形磨耗使車輪輪重減載率最大值增大67.7%,嚴重降低了列車運行的安全性,也使橋梁跨中橫向和豎向加速度最大值分別增大2.74倍和2.27倍。

(2)車輪多邊形磨耗幅值增大使車橋耦合系統的振動響應顯著增大。車輪多邊形磨耗幅值由0.02 mm增大至0.08 mm時,列車輪重減載率、橋梁跨中橫向和豎向加速度、鋼軌中點橫向和豎向加速度分別增加76.5%、174%和127%、47.3%和83.1%。隨著列車運營里程增加,車輪多邊形磨耗幅值將隨之增加,這可能會使得車橋耦合系統的振動進一步加劇,降低列車運行的安全性和橋梁結構的耐久性。

(3)車輪多邊形磨耗階數增加也會使車橋耦合系統的振動響應顯著增大。車輪多邊形磨耗階數由1階增大至4階時,列車輪重減載率、橋梁跨中豎向加速度、鋼軌中點橫向和豎向加速度分別增加116%、389%、82.0%和170%。特別地,列車以200 km/h速度運行時,3階車輪多邊形磨耗引發橋梁橫向共振使得橋梁跨中橫向加速度顯著增大,是4階車輪多邊形磨耗作用時的2.74倍。