考慮模糊多目標優化的風電場無功電壓分區控制

王 瑋, 楊 健, 任國瑞, 任 鑫, 王 華

(1.華北電力大學 控制與計算機工程學院,北京 102206;2.中國華能集團清潔能源技術研究院有限公司,北京 102209)

我國的陸上風能資源集中于“三北”地區,這些集群式開發的風電匯集區域內多為輻射型連接,匯集線路較長,并且少有甚至沒有負荷接入,屬于典型的弱連接送端系統[1-2]。由于風電場在向系統輸送有功功率的同時可能吸收大量的無功功率,而無功功率與電壓穩定性具有強相關性,因此大型風電場的接入會對電網電壓穩定性產生重要影響,甚至可能危及電網安全運行[3-5]。

目前,并網風電場都要求具有自動電壓控制(AVC)功能。一方面,安裝機械投切式電容器組、靜止無功補償器(SVC)、靜止無功發生器(SVG)等無功補償裝置[6];另一方面,挖掘風電場自身的無功調節能力,例如:針對永磁直驅風場可實現靈活無功控制,雙饋式風場可通過有功無功解耦,動態調節無功輸出能力[7-8],為電網提供無功電壓支撐。

近年來,國內外學者針對風電場無功電壓控制問題開展了廣泛研究。文獻[9]～文獻[10]以電壓波動、網損指標建立無功優化模型,通過優化算法尋找無功補償裝置與每臺機組的無功補償量,有效平抑了系統內的電壓波動。崔楊等[11]將風電場用一臺等值機組等效,極大提高了計算速率,并且通過東北某省13個子風場組成的風電場群為例,驗證了策略的可行性。栗樹材[12]提出考慮機組尾流效應的聚類模型,對整個風電場進行分區處理,同時保證計算的準確性和時效性。文獻[13]～文獻[15]將無功發生設備的裕度作為目標函數進行優化,使得風電場有充足的無功裕度來保證風電匯集系統的安全穩定運行。上述研究均對風電場的無功電壓分區控制策略進行了有益探索,在降低風電場無功優化求解維度的同時也保證了一定的精度,但卻忽略了各區內部風電機組無功功率水平的不同,這可能會導致區內機組的無功裕度水平參差不齊。

配電網的無功優化問題是一個多目標非線性問題的集合[16],涉及多個控制變量與約束條件,目前研究的無功優化方法主要是智能算法,例如傳統的遺傳算法(GA)[17-18]、粒子群算法(PSO)[19]、禁忌算法(TS)[20]。余健明等[20]對傳統的TS進行了一定改進,提出了一種自適應長度的禁忌搜索算法對含風電機組的配電網進行無功優化,其中自適應長度方法加速了禁忌搜索算法的求解過程。但受限于傳統算法的局限性,以及無功優化問題的高維數與復雜優化策略空間的特性,傳統算法已難以滿足實時在線優化的高精度、高速度要求。

基于上述研究,筆者提出了一種考慮模糊多目標優化的風電場無功電壓分區控制方法。該方法基于有功功率對風電場進行分區降維,定義了分區無功裕度指標;建立了綜合考慮分區無功裕度、節點電壓和系統網損的模糊多目標優化模型;提出了一種可大范圍全局快速尋優的自適應遺傳禁忌算法(AGATS),通過重新定義交叉與變異概率提升了尋優的全局性,通過引入TS改善了尋優準確性。

1 風電場無功電壓控制策略框架

風電場無功電壓控制策略如圖1所示。其中,Uref為電網電壓指令,UWF為風電場內機組端電壓信息,UPCC為風電場匯集母線的電壓信息,QWF為風電場的無功功率信息,PWF為風電場的有功功率信息,QWF,ref為風電場的無功功率需求量,QI,lim為各分區的無功限值,QI,ref為各分區的無功補償量,Qi,ref為各風機的無功補償量,QSVG為SVG的無功補償量。圖1中,風電場呈6條饋線,每條饋線含11臺雙饋感應異步發電機組(DFIG),所有的饋線都連接在一條匯集母線上,匯集母線額定電壓為35 kV,匯集母線再經過升壓變壓器T1及外送線路接入電網,電網額定電壓為220 kV。

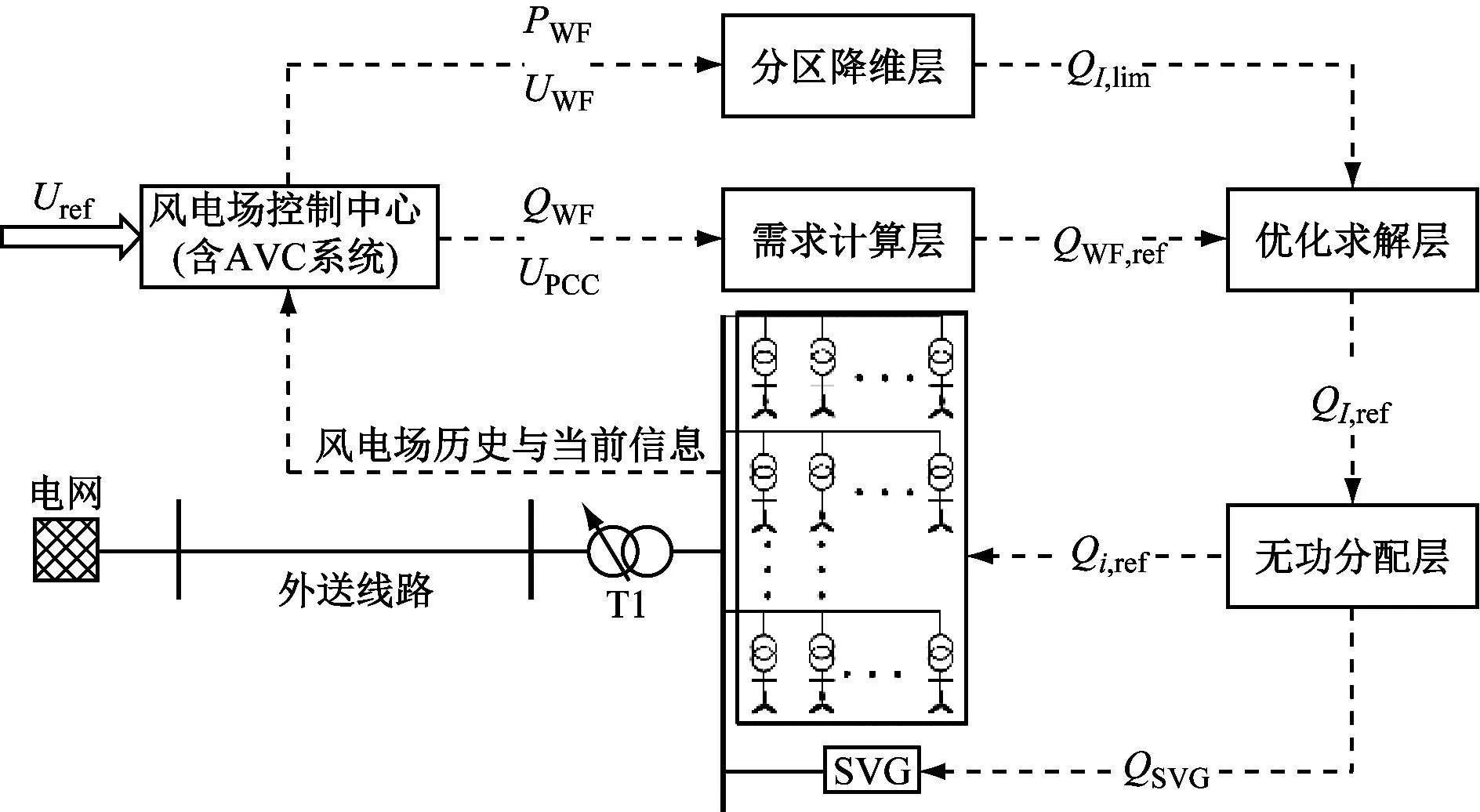
圖1 風電場無功電壓控制策略Fig.1 Reactive power and voltage control strategy for wind farms

所提出的控制策略的步驟如下:(1)基于風電場無功功率信息和匯集母線電壓信息計算無功需求量;(2)基于風電場有功信息和場內機組端電壓信息對風電場進行無功限值計算和分區降維操作;(3)定義分區無功裕度指標、節點電壓波動指標和網損指標,使用本文所提算法進行模糊多目標尋優,獲得各分區和SVG的最優無功目標值;(4)在各分區按照等裕度方法分配無功補償量。本文所用風電場有功信息均為有功預測信息。

1.1 需求計算層

根據匯集母線在相鄰測量時刻的電壓信息,以及風電場在相鄰測量時刻的無功功率信息,可估算出風電場輸出無功相對于匯集母線電壓的控制靈敏度K1:

(1)

式中:U1、Q1分別為上一個測量時刻的匯集母線電壓及風電場無功輸出量;U2、Q2分別為當前測量時刻的匯集母線電壓及風電場無功輸出量。

進而可得風電場當前時刻的無功補償量Qref為

(2)

式中:UPCC,ref為匯集母線的電壓指標,本文設為35 kV。

1.2 分區降維層

1.2.1 DFIG的無功調節特性

通過分析DFIG的運行特性,可知DFIG的無功調節能力主要受有功功率、機組容量和變流器電流限制等約束,即DFIG的無功極限由定子和網側換流器共同決定。忽略定子電阻可得定子無功極限值[21]為

(3)

式中:Qsmax為定子側的無功功率上限;Qsmin為定子側的無功功率下限;Ps為定子側有功功率;Us為定子端電壓;Xs為定子全電抗;Xm為勵磁電抗;Irmax為轉子側變流器的電流限值。

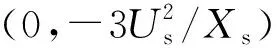
圖2 DFIG定子無功極限Fig.2 Reactive power limit of DFIG stator

網側換流器的無功調節能力主要由網側換流器的極限容量和風電機組的轉差率決定,其輸出無功的極限為

(4)

式中:Qwmax為網側換流器的無功功率上限;Qwmin為網側換流器的無功功率下限;Smax為網側換流器的極限容量;s為DFIG的轉差率。

因此,最終可得單臺DFIG的無功調節極限為

(5)

式中:Qmax為DFIG的無功功率上限;Qmin為DFIG的無功功率下限;Qlim為DFIG的無功功率調節范圍。

1.2.2 考慮有功特性的風電場分區

DFIG的無功極限與其有功功率密切相關,而在進行風電場無功優化調度方案的求解過程中,無功極限也是一個重要的約束條件,并且機組的無功極限也與分區無功裕度指標有著密切關系,因此筆者利用不同DFIG的有功功率信息對風電場進行實時的聚類分區。

K-means聚類算法的基本思想是隨機選取K個初始質心,然后對所有樣本進行聚類,具體步驟可見文獻[22]～文獻[23]。對于質心個數K的選取,本文采取手肘法進行最優分區數的選取,手肘法的核心指標是誤差平方和,即

(6)

式中:SSSE為所有樣本的誤差平方和,代表了聚類效果的好壞;p為Ci點群的樣本點;Si為Ci點群的質心。

手肘法的基本思想是:SSSE與K的關系圖呈現手肘形狀,肘部對應K就是數據的最佳聚類數。選取“三北”地區某風電場隨機6個時刻的有功功率信息進行聚類,取K為1～8時,對應的SSSE如圖3所示。

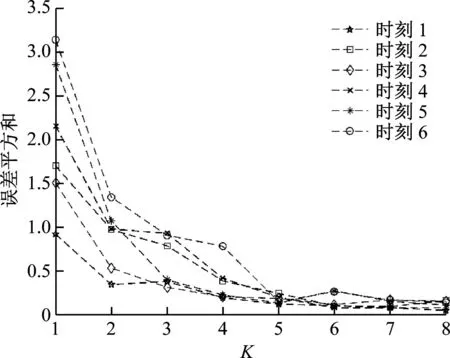
圖3 不同K對應的SSSEFig.3 SSSE values corresponding to different K values

由圖3可以看出,當K小于5時,SSSE的下降幅度較大;當K大于5時,SSSE的下降幅度驟減。因此選取分區數為5進行實時分區。

1.3 無功分配層

在實際的風電場中,一般都配有無功補償設備,但本文所提策略旨在最大限度地發揮DFIG的無功調節能力,因此優先調用DFIG。各場區DFIG與SVG的具體分配方式如下:

(1) 當無功需求量在DFIG的安全運行無功極

限范圍內時,第i號DFIG的無功功率和SVG無功補償量分別為

(7)

式中:Qi-DFIG和Qi-lim分別為第i號DFIG的無功功率及其無功功率極限;QI-ref和QI-lim分別為第I號場區的無功補償總量和無功補償總極限。

(2) 當無功需求量超出了DFIG的安全運行無功極限范圍內時,第i號DFIG的無功功率和SVG無功補償量分別為

(8)

2 無功電壓的模糊多目標優化模型

2.1 目標函數

本文定義了分區無功裕度指標用以描述風電場電壓運行的安全裕度,同時從運行穩定性和經濟性的角度,定義了節點電壓波動指標和網損指標,建立了風電場無功模糊多目標優化模型。

2.1.1 分區無功裕度指標

當風電場進行分區操作后,控制變量為場區的無功功率總值,約束條件也變為場區的無功功率總極限,定義分區無功裕度指標f1為

(9)

式中:L為分區數;NI為第I號場區的風機數量。

由于風電場內部風電機組的無功功率和饋線電纜長度不同,導致機端電壓會有一定的差異。為了能夠更好地考察每臺風電機組的電壓穩定性,提出了如下的節點電壓波動指標f2:

(10)

式中:N為風電場中所有節點的集合,Vi,ref為節點i的參考電壓,Vi為節點i的實時電壓。

2.1.3 網損指標

為保證風電場運行過程中的經濟性,定義了風電場網損指標f3:

(11)

式中:Gij為節點i和j的互導納;Vj為節點j的實時電壓;θij為節點i和j的電壓相角差。

對上述3個指標進行歸一化:

(12)

式中:fi,i為歸一化后的指標有效值;hi和li分別為預先計算的3個指標中的最大值與最小值。

2.2 模糊優化模型

為解決多目標優化的權重系數選擇難題,本文引入模糊規則定義無功電壓的模糊多目標優化模型。各目標函數對應的權重系數函數為

傳統的無線傳感器網絡(Wireless Sensor Network,WSN)中傳感器節點由電池供電，能量容易耗盡，網絡生存周期較短，限制了其實際應用場景[1～3].無線可充電傳感器網絡作為目前的研究熱點，通過捕獲外界能量為傳感器供電，以解決上述問題.射頻能量作為最具研究前景的能量之一，節點可捕獲專用的射頻能量或環境的射頻能量轉化為電能給傳感器的收發數據等正常工作供能.

(13)

式中:Si為目標函數的最小值;Sj為目標函數的最大值;δi、δj為系統操作員期望的目標函數理想變化量;下標i=1,j=2,3,對應不同的目標函數。

f1、f2、f3選用半梯形折線作為權重系數函數,如圖4所示。

圖4 各目標函數對應的權重系數函數Fig.4 The weight coefficient functions corresponding to each objective function

模糊模型中權重系數的優化步驟具體如下:

(3) 以網損指標最小為目標函數,求得f?1、f?2、f?3。

(4) 在前3步的基礎上對各單目標函數進行一定程度的收縮,確定δi和δj。

(14)

式中:ε1、ε2、ε3∈[0,1],可根據系統操作員的要求進行不同程度的收縮,取值越大表明對目標函數的要求越高。

(5) 在多目標尋優過程中,根據各目標函數值實時調整相應的權重系數。

綜上,總目標函數F為

(15)

式中:α(f1,1)、α(f2,2)和α(f3,3)分別為分區無功裕度指標、節點電壓波動指標和網損指標的權重系數。

2.3 約束條件

2.3.1 等式約束

潮流方程約束[24]為

(16)

式中:Pi為節點i的有功功率;Bij為節點i和j的自導納;Qi為節點i的無功功率。

無功功率平衡約束為

(17)

式中:M為總風機數量。

2.3.2 不等式約束

不等式約束主要包括節點電壓上下限約束、DFIG的無功功率上下限約束、SVG功率的上下限約束,即

(18)

式中:Vi,max和Vi,min為節點i的電壓幅值上下限;Qi,max和Qi,min為i號風機無功功率的上下限;QSVG,max和QSVG,min為無功補償設備SVG功率的上下限。

3 多目標優化算法

3.1 AGATS

為提升尋優的全局時效性和準確性,筆者針對上述模型提出了一種可大范圍全局快速尋優的AGATS。

具體實現過程如下:

(1) 生成初始解。在給定的不等式約束范圍內,隨機生成一組數據X(IA,KA),其中IA為父代種群的規模,KA為變量數量,然后對種群中個體進行處理:

(19)

式中;X(i,j)為原始數據中第i個個體的第j個變量值;X′(i,j)為經過約束處理之后的變量值。經過驗算可知處理后的數據滿足:

(20)

(2) 選擇和交叉操作。本文采用多精英保留方案和二元錦標賽方案結合的選擇方法,以及雙點交叉的交叉方法,具體步驟可見文獻[25]～文獻[27]。

(3) 自適應交叉與變異策略。定義了反映種群密集程度的變量f′:

(21)

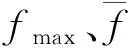
種群會隨著算法的迭代逐漸變得密集,且在前期變化較快,后期變化較慢。交叉操作適合在種群離散時使用以增加種群多樣性,而變異操作適合在種群密集時使用,以維持種群多樣性。因此,定義了交叉與變異概率的自適應公式:

(22)

式中:pcmax、pcmin、pmmax和pmmin分別為交叉與變異概率的最大和最小值;w為自適應系數,用以平緩交叉概率pc與變異概率pm的變化。

(4) 禁忌變異算子(TSM)。對種群中的個體隨機進行TSM變異操作,具體如圖5所示。生成鄰域解Xnear的公式為

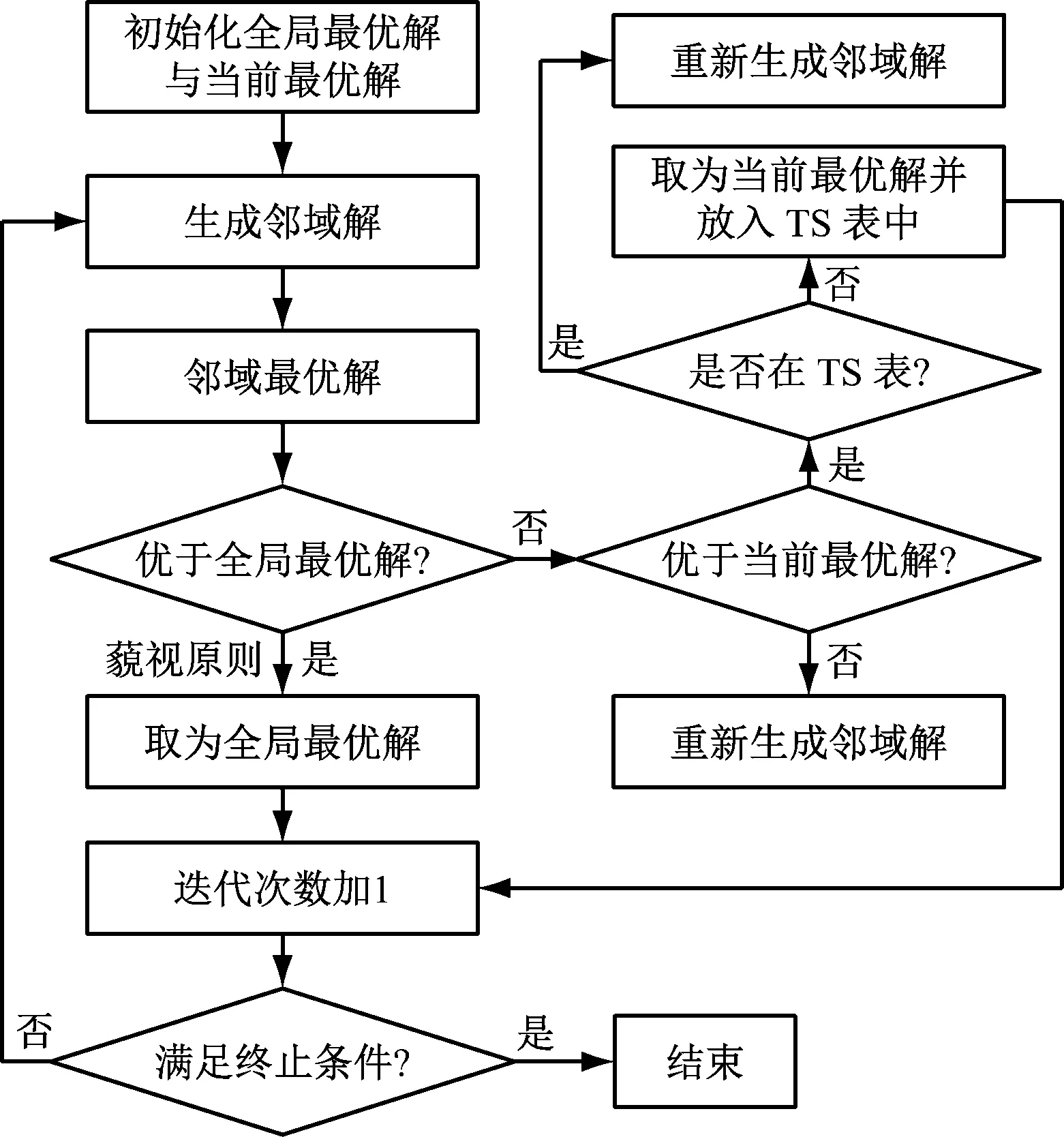
圖5 TSM變異Fig.5 TSM mutation

Xnear(i,j)=x(i,j)+(2r-1)v(xh(i,j)-xl(i,j))

(23)

式中:x、xh、xl分別為當前解和上下限;r為0到1的隨機數;v為自適應系數。

(5) TS表處理。建立局部TS表,采用TS表記錄算法操作的結果,避免無效動作。

(6) 停止原則。種群連續50步無法搜索到更優值或者達到迭代次數上限時則停止。

算法的基本流程如下:

(1) 輸入設定值:仿真步長L,種群規模IA,變量數量KA,交叉與變異概率的最大值和最小值pcmax、pcmin、pmmax和Pmmax。

(2) 初始化種群:基于不等式約束生成初始種群X,根據式(19)對種群進行等式約束處理。

(3) 種群迭代:通過選擇操作更新父代種群;根據式(21)更新離散度函數;根據式(22)更新交叉與變異概率;對個體進行交叉和TSM變異操作并根據TS表判斷本次操作是否有效;最終滿足終止條件時結束算法循環。

3.2 算法性能比較

通過測試函數能夠測試出改進算法的全局性、時效性和準確性。本文將標準二元多峰函數改寫為:maxf=x2sin(2πx1)+x1cos(2πx2)+x3sin(2πx5)+x5sin(2πx4),xi∈[-3,3]。該函數為五元多峰函數,變量個數與本文優化策略一致,峰形高低起伏,不定跳躍性,有多個局部極大點。分別采用GA、TS、傳統GA-TS與本文所提算法進行求解計算。算法參數設置見表1,其中CA為鄰域解個數,結果如圖6所示。

表1 算法參數設置Tab.1 Algorithm parameter settings

圖6 不同算法結果對比Fig.6 Comparison of results in different algorithms

由圖6可知,由于GA算法的全局搜索能力強,因此能夠快速得到最優解,在全局時效性方面,GA>TS;而TS算法由于其強局部搜索能力和爬山能力使得TS算法最終可以得到更優的解,在準確性方面,TS>GA。傳統GA-TS算法將GA算法和TS算法簡單地融合在一起,在全局時效性方面,GA>GA-TS>TS,在準確性方面,GA-TS>TS>GA。本文所提算法可自適應更新交叉與變異概率,減少冗余計算量,并通過保證種群多樣性增加算法的準確性,在全局時效性方面,AGATS>GA>GA-TS>TS,在準確性方面,AGATS>GA-TS>TS>GA。AGATS算法的流程圖如圖7所示。

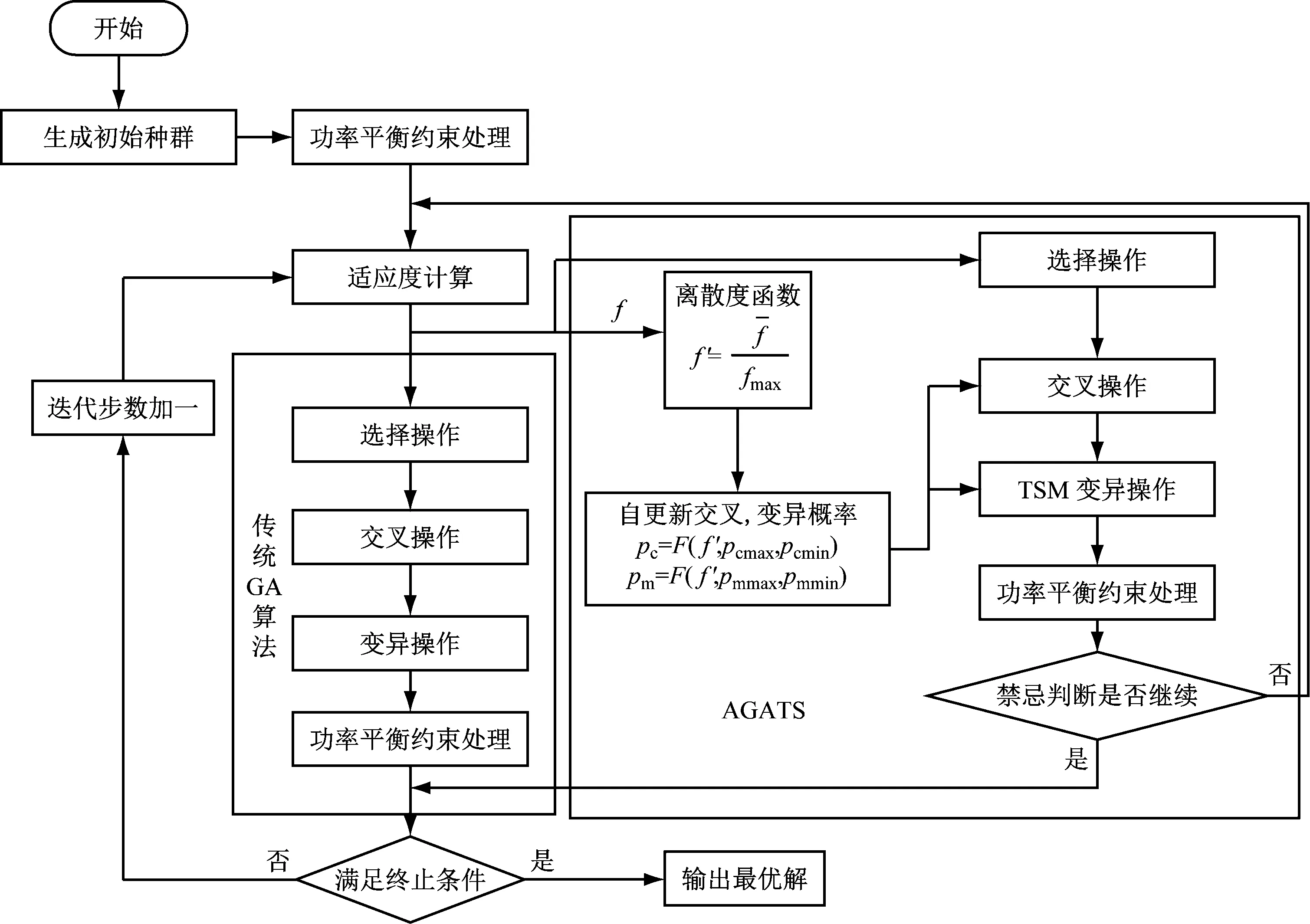
圖7 算法流程圖Fig.7 Algorithm flow chart

4 仿真分析

4.1 系統說明及參數設置

以“三北”地區某風電場為例,電網電壓為220 kV,風電場內有66臺1.5 MW的雙饋風電機組,機組之間距離0.7 km,線路類型為LGJ-35,如圖8所示。按一機一變配置容量為1.6 MV·A的箱式變壓器。風機發出的功率經匯集母線匯總后通過容量為120 MV·A的變壓器升壓,然后經過120 km的外送線路與電網連接,線路型號為LGJ-185。風電場升壓站裝有1臺容量為±10 MV·A的SVG。

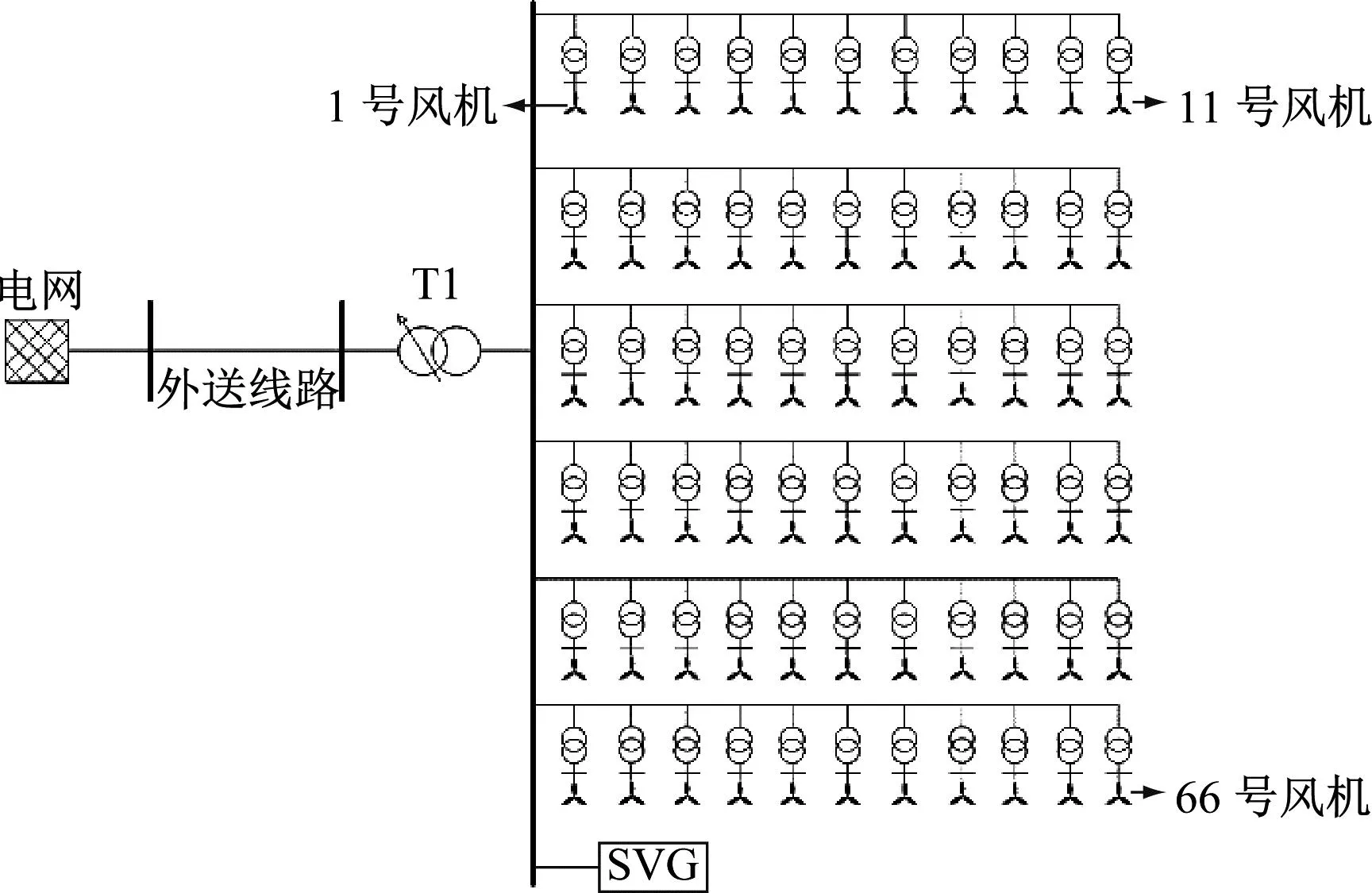
圖8 風電場示意圖Fig.8 Schematic diagram of wind farm

4.2 控制效果分析

筆者設置了2種控制方式進行對比分析:

(1) 方式1,風電場分區降維+傳統GA。算法相關參數與表1所示的參數相同。控制周期為10 min。

(2) 方式2,風電場分區降維+AGATS。算法相關參數與表1所示的參數相同。控制周期為10 min。

2種方式下風電場內的有功功率信息及無功功率信息如圖9所示,匯集母線電壓如圖10所示,節點電壓波動指標如圖11所示,某時刻下的機組端電壓如圖12所示,部分時刻的風電場分區無功裕度指標如圖13所示。優化結果對比見表2。

表2 不同控制方式的優化結果對比Tab.2 Comparison of optimized results by different control modes

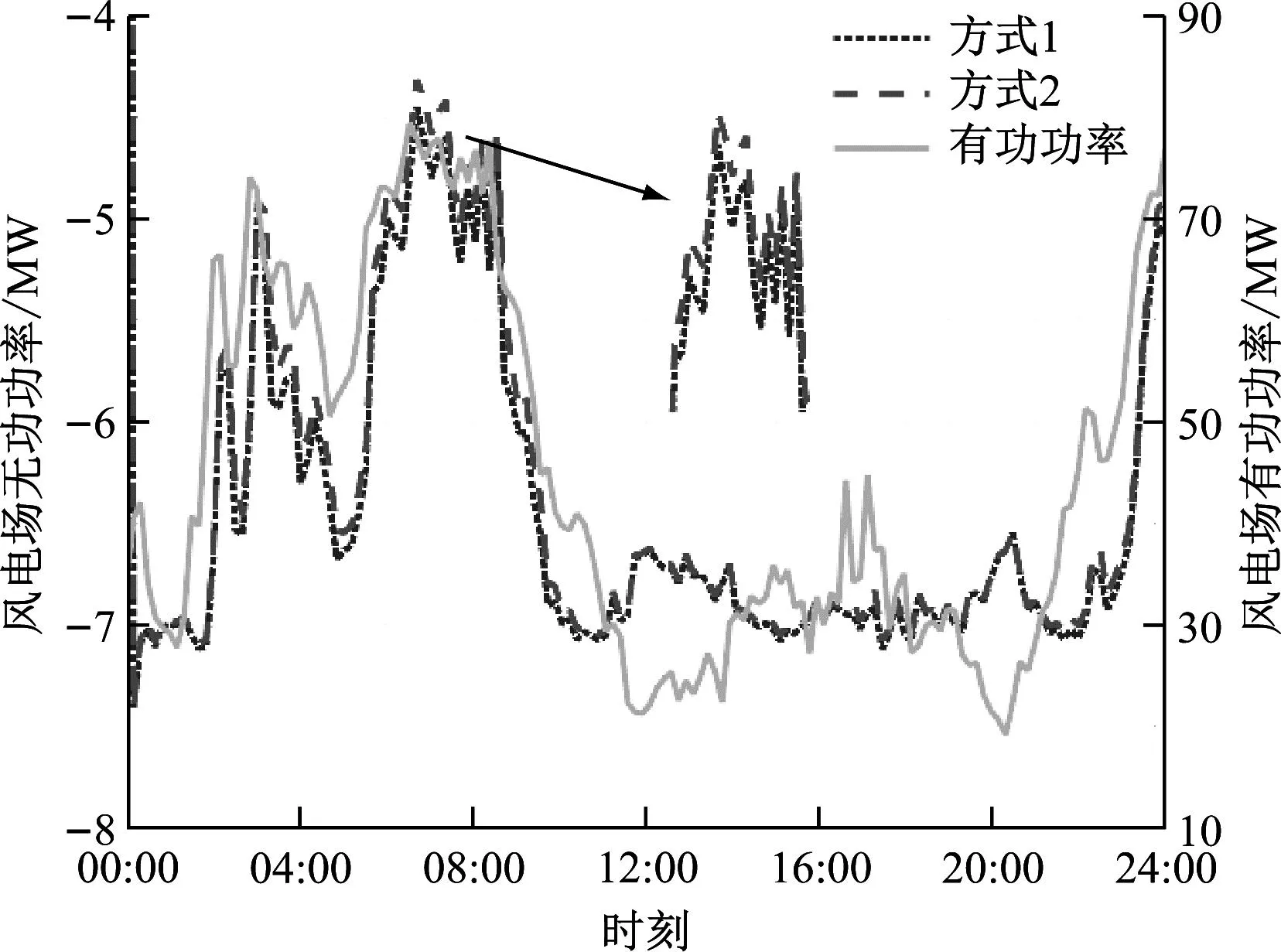
圖9 無功功率和有功功率Fig.9 Reactive power and active power

圖10 匯集母線電壓幅值Fig.10 Voltage values of PCC bus

圖11 節點電壓波動指標Fig.11 Nodal voltage fluctuation index

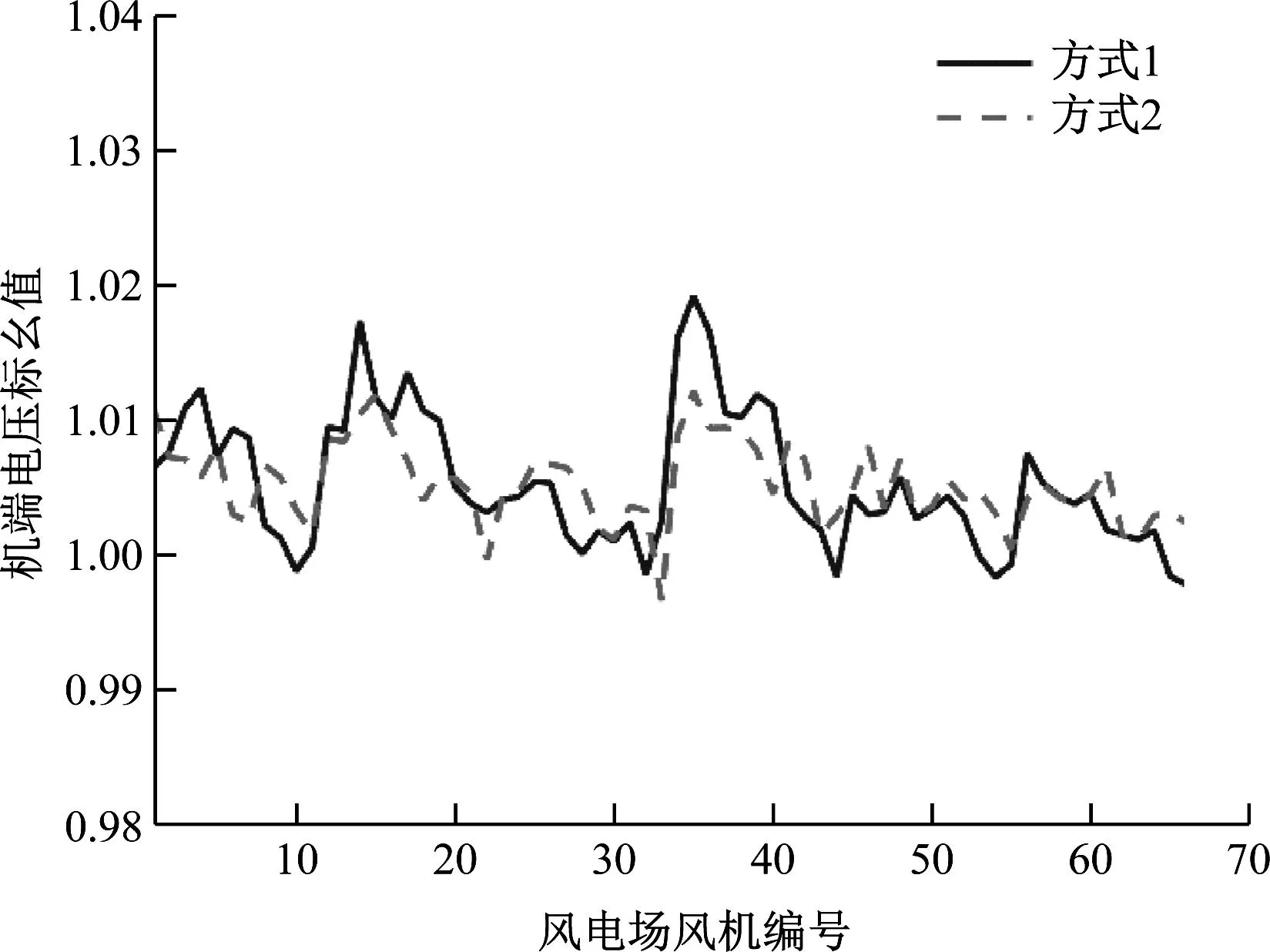
圖12 機組端電壓值Fig.12 Voltage values of each wind turbine

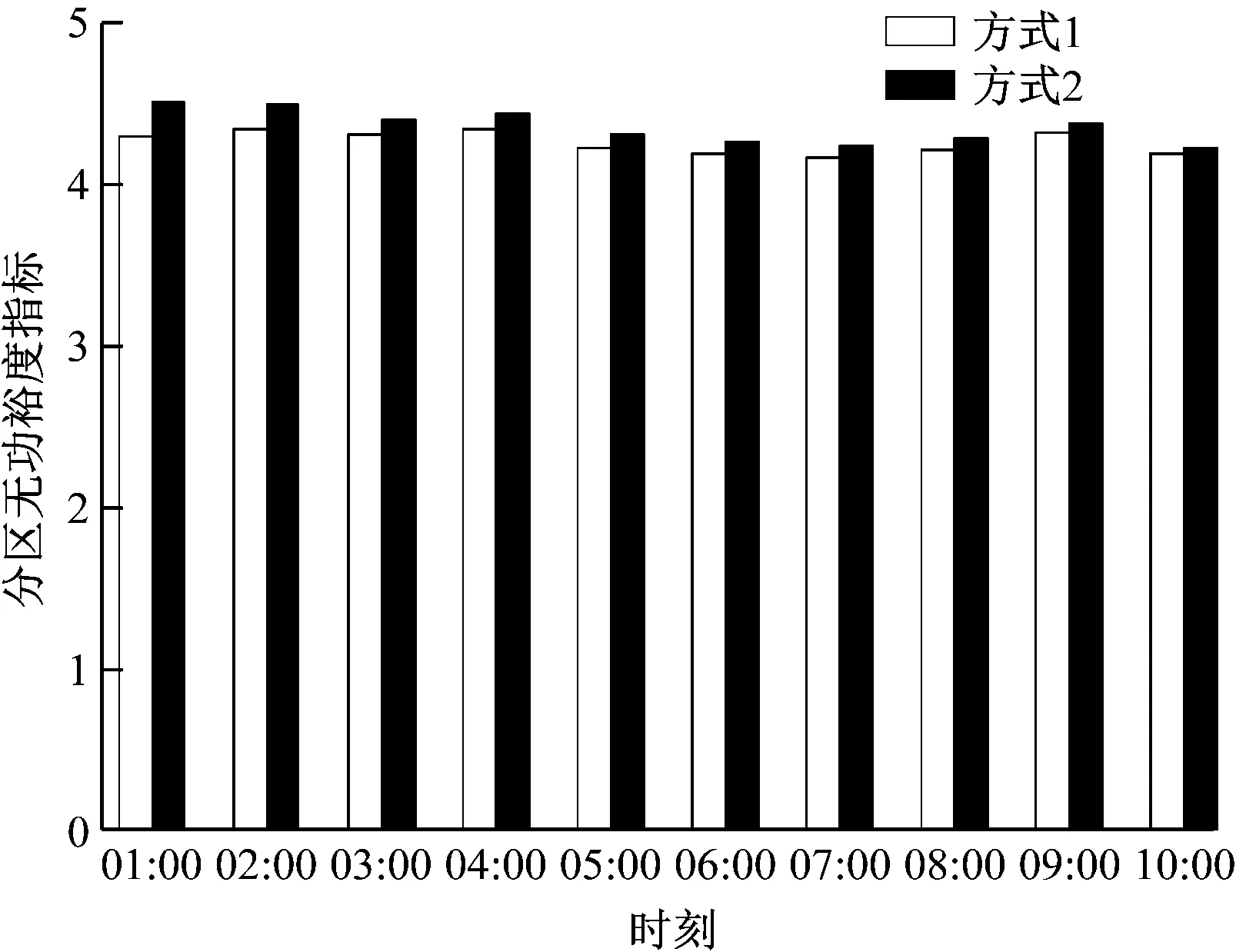
圖13 部分時刻風電場無功裕度Fig.13 Partial reactive power margin of wind farms

由圖10可知,加入無功補償后的2種方式均使匯集母線電壓幅值與電網指令基本重合,證明無功補償有助于匯集母線的電壓穩定。由仿真結果可知,方式2下的節點電壓波動指標均值相對于方式1降低了0.003 4,優化比例為4.69%;方式2下的風電場分區無功裕度均值相對于方式1增加了0.136,優化比例為3.27%,證明所提風電場無功電壓協調優化方法是可行的,且相較于傳統智能算法具有更優的效果。需要說明的是,由于本文策略控制的目標側重于穩定系統內的電壓水平和確保系統運行的安全裕度,導致只有在高風速時段才能表現出降低網損的效果,按照式(11)計算所得的高風速時段的網損如圖14所示。

圖14 高風速時段網損示意圖Fig.14 Diagram of network loss during high wind speed period

5 結論

(1) 本文以風機的有功出力信息進行分區,最終的結果驗證了該分區方法的可行性和實用性,這有助于大型風電場的優化調度方案求解。

(2) 本文所提優化算法相較于傳統算法具有更好的優化效果,且算法本身具有一定通用性,其他進行優化方案求解的領域也可使用該算法。

(3) 建立了由分區無功裕度指標、節點電壓波動指標及網損指標組成的模糊多目標優化模型,從多方面改善了風電匯集系統的靜態電壓穩定性。結果表明,該方法下的節點電壓波動指標均值相較于傳統方式降低了4.69%,提高了電壓的穩定性,風電場無功裕度均值相較于傳統方式增加了3.27%,提高了運行的安全裕度。