一道填空題的改編命制歷程與反思

東莞市第十高級中學(523981) 許浩杰

隨著高中數學新課程標準的落實,有利于發展學生數學核心素養的新題型得到了開發與使用. 近年,從高考題到各省市的高考模擬題,大家都在探索研究不同試題類型的命制方式. 在改編一道填空題中,經歷了從封閉性問題到開放性問題的調整,在此談談對兩類題目命制的體會和反思.

1 關于封閉性問題與開放性問題

高考數學具體試題類型一般包括封閉性問題與開放性問題兩類試題類型.

在我國的數學教學與評估中使用的問題主要是計算題、論證題、常規題的應用題和填充題,這些問題的答案只有正確與不正確(包括不完整)兩種,并且正確的答案是惟一的.這些問題給出的條件往往都是用得著的,而且只用一次. 這一類問題叫封閉性問題(closed problem),它是我國數學教學的基礎. 此類試題能體現“回課本、重概念、考通法”,體現數學試題的普適性. 試題解題方法注重通性通法,貼近日常教學,突出能力和素養的考查.

開放性問題(open-ended question),又稱構造性反應. 它要求被試創造一個反應,而封閉性問題則要求被試回憶、選擇一個反應. 開放性問題的特點是結論、條件、思路都是開放的. 而結構不良題就屬于開放性問題,是指試題開放設問,問題的條件、數據等部分缺失或冗余,問題目標界定不明確,要求學生綜合運用所學知識進行探究. 結構不良題類型包括條件開放、結論開放、條件結論均開放等.

2019 年教育部考試中心發布的中國高考評價體系中指出,高考重點考查學科的核心素養,進一步關注學生的知識應用、數學探索等方面的能力. 結構不良題給學生提供了開放的探究空間,能很好地培養學生的思維創造力.

2 題目命制歷程

2.1 試題原題與解析

試題原題如圖1, 在棱長為3 的正方體ABCD-A1B1C1D1中,點N在該正方體的棱上運動,則有____個滿足條件的點N,使得點N到平面A1BC1的距離為.

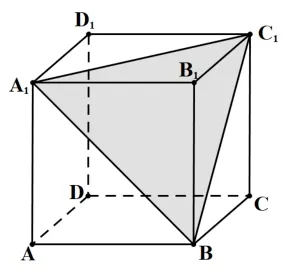
圖1

解析: 在正方體ABCD-A1B1C1D1中, 當點N運動到與點B1重合時, 三棱錐B1-A1BC1的體積為:(h為點B1到平面A1BC1的距離),而等邊三角形ΔA1BC1的面積為:

由等體積法得:

圖2

綜上所述, 有4 個滿足條件的點N, 使得N到平面A1BC1的距離為.

在解決上面這道題目時,發現隨著點到直線的距離的變化,滿足條件的點的數量也將隨之變化. 這個發現讓筆者解后久久回味,在腦袋里醞釀著如何改編該題.

2.2 改編版本1: 常規題

第一個想法是將原題改編成常規題,包括兩個問,形成難易梯度,其中第一個問相對容易,占2 分,第二個問難度較大,需要學生畫圖、計算、分情況探究等,占3 分. 改編的思路是第一問求正方體一個特定的頂點到指定平面的距離,第二個問打破原題的那幾個頂點的特殊性,引導學生去探求滿足條件的點的數量.

改編題1在正方體ABCD-A1B1C1D1中,棱長為1,點P在該正方體的棱上運動,則當點P運動到與點B1重合時,點P到平面A1BC1的距離為____; 另外,當點P到平面A1BC1的距離為時,有____個滿足條件的點P.

解析: (1) 在正方體ABCD-A1B1C1D1中, 當點P運動到與點B1重合時,三棱錐B1-A1BC1的體積為:(h為點B1到平面A1BC1的距離),而

由等體積法得:

(2)由(1)知點B1到平面A1BC1的距離為,連接AD1,AC,CD1,有平面A1BC1與平面AD1C平行,同理可計算出點A,D1,C到平面A1BC1的距離也為.當點P運動到與點D重合時,

同理可得點D到平面A1BC1的距離為. 這是正方體棱上動點P到平面A1BC1的最大距離.

根據點到平面距離的變化,可以分成以下4類情況:

1)當點P到平面A1BC1的距離為時,有4個滿足條件的點P.

2)當點P到平面A1BC1的距離在范圍中時,可在平面A1BC1與平面AD1C之間作平行平面α, 可知平面α與正方形的棱有6 個交點; 同理, 在點B1與平面A1BC1之間作平面β與平面A1BC1平行,可知平面β與正方形的棱有3 個交點. 故有9 個滿足條件的點P,如圖3 所示.

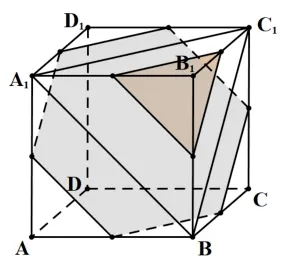
圖3

3)當點P到平面A1BC1的距離在范圍中時,同理有3 個滿足條件的點P,如圖4 所示.

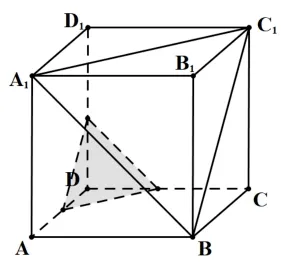
圖4

4) 當點P到平面A1BC1的距離為時, 有1 個滿足條件的點P. 故當點P到平面A1BC1的距離為時, 屬于第二類情況, 故有9 個滿足條件的點P.

這個常規題的改編版本由原題的一問調整為兩問. 考查學生立體幾何的綜合應用,綜合考查線面垂直與面面平行的判定與性質等知識點,訓練學生畫簡圖、靈活使用等體積法求點到平面距離、利用平面動態平移等技巧,考查學生轉化與化歸等思想方法,綜合考查學生分析、解決問題等能力.

兩個問的設定,使題目有了梯度性,從特殊性走向拓展,可進一步延伸到題目的其他情況;第二小問設置數值,引導學生探究題目的不同情況,并最終得到時,屬于第二類情況,鍛煉了其邏輯推理能力.

2.3 改編版本2: 結構不良題

經過第一版常規題的改編,筆者覺得還不能很好地通過題目引導學生去探索發現. 題目的要求相對直接,學生被動式地完成題目,沒能更好地發揮題目隱藏的學生可多情況破題的作用. 從而有了下面第二版本的改編題.

改編題2在正方體ABCD-A1B1C1D1中,棱長為1,點P在該正方體的棱上運動,則當點P運動到與點B1重合時,點P到平面A1BC1的距離為____; 另外,當點P到平面A1BC1的距離為____(可填具體數值或區間范圍)時,有____個滿足條件的點P.

第二版本的題目主要在于第二小問調整為結構不良題,讓學生隨著題目的探究,鍛煉了其邏輯推理能力,可呈現學生不同的思考成果,也讓答案有了更多的可能性.

題目編好之后, 考慮到題目3 個空共5 分, 第一個問2分,第二問結構不良占3 分,分值和考試時學生完成此題所用的時間量相關性太弱,且第一問所求的距離求出來后可以直接套入第二問的解答中,從而失去了命制本來計劃達到的解答多樣性的效果. 此版本改編題目還得改.

為了讓題目更好地引導學生探究,同時簡化題目三個空的設置,第三版的題目刪掉了第一個問,保留了后面的問題.

改編題3在正方體ABCD-A1B1C1D1中,棱長為1,點P在該正方體的棱上運動,當點P到平面A1BC1的距離為____(可填具體數值或區間范圍)時,有____個滿足條件的點P.

此版改編題,雖然出現了多種解答結果,但是學生畫圖可敏感發現P到平面A1BC1的距離最大的點為點P與點D重合時,且只有1 個滿足條件的點. 題目有了這個特殊情況,導致學生都奔著點D去解題,沒能達到結構不良題所起的作用,得繼續調整修改.

為此,筆者查閱并學習了近年高考題中結構不良題的命制形式,通過設置3 個不同距離數值,改編成第四版題目.

改編題4在正方體ABCD-A1B1C1D1中,棱長為1,點P在該正方體的棱上運動,在①當點P到平面A1BC1的距離為, ②當點P到平面A1BC1的距離為,③當點P到平面A1BC1的距離為這三個條件中任選一個,補充在下面問題中,并給出相應結論.

在正方體ABCD-A1B1C1D1中,棱長為1,點P在該正方體的棱上運動,____(三選一,填序號①或②或③)時,有____個滿足條件的點P.

最后版本的改編題,通過不同條件的設定,使題目情況多樣化,給學生的探究帶來不同的指引,從原題的特殊性研究走向多方向探究,引導學生進一步拓展到所有情況. 考慮到題目每個條件的難度和題目的科學性,沒有把全部情況放開讓學生自由選擇,只提供了3 個不同的數值作為解題條件.

至此,改編的題目雖還有瑕疵,但也大致展現了結構不良題的優勢,給學生解題提供了多種可能性.

3 幾點思考

通過以上題目的改編歷程,從常規題到結構不良題,可以發現:

首先,題目命制要注意梯度性. 通過第一版本常規題的改編,題目從一個問調整為兩個問,形成難度差異,使題目有了梯度,有利于學生由易到難層層遞進解決問題.

其次,題目命制要注意指向性. 在編制第二版本結構不良題時,設置的3 個空使得題目冗長且第一個問影響到后續解題的方向,通過改編,筆者及時對題目進行調整,命制時考慮問題指向清晰,避免學生思維受限制,防止題目出現設計之外的思維漏洞.

特別的,題目命制要注意科學性. 在命制結構不良題時,作為命題者,題目結論的每種可能性都要提前研究透徹,避免出現難度差異過大的情況,最好能使每個解決方案在任務耗時、操作難度、思維水平等方面都相對持平.

總之,在題目命制的過程中,命題者應落實以德樹人的宗旨,基于高中數學新課程標準的理念,以培養學生數學核心素養為指導,充分發揮題目對提升學生數學核心素養的積極作用.