基于靈敏度分析的諧波治理設備多目標優化配置方法

江友華,宮唯佳,曹以龍,楊興武,吳衛民

(1.上海電力大學, 上海 200090; 2.上海海事大學, 上海 200120)

0 引 言

隨著國民經濟的發展,越來越多的非線性負荷(如工業煉鋼爐、工業交直流電機、大功率整流器、UPS、電動汽車充電樁)和分布式電源(如用戶側風機、光伏、蓄電池、燃料電池的大功率逆變器)接入配電網[1-2],由此導致了電壓波形畸變、諧波損耗激增、電能質量下降等一系列諧波污染問題[3-4]。另一方面,隨著生活水平的提高,精密化的電源和負荷設備,對配電網的電能質量較敏感,對諧波治理的需求更加迫切[5-6]。有別于無源濾波器,有源電力濾波器(Active Power Filter, APF)能夠動態補償各次諧波分量,而且不易受系統阻抗影響,近年來廣泛應用于配電網的諧波抑制[7]。然而,APF接入配電網的位置與容量大小有所不同,對多諧波源并存下諧波治理的效果有較大影響,所以有必要探究有源濾波器選址和容量大小優化的問題[8]。

當前,已有文獻探究了濾波器的選址定容問題。文獻[9]通過互信息提取公共點諧波的特征信息并定位諧波源,采用自適應模糊粒子群算法求解濾波器的最優安裝位置;進一步,為了改善粒子群算法很容易陷入局部最優的問題,文獻[10]對粒子群算法做出了優化增加了隔離小生境理論,求解濾波器的選址定容模型;文獻[11]是利用網絡固有理論和綜合評估方法對無源和有源濾波器進行選址,再根據優化模型定容參數;文獻[12]根據諧波狀態下的系統和負荷的戴維南等值模型,用于確定濾波器的最優容量。然而,上述文獻的智能算法優化選址定容計算效率低,其余選址方法也大部分針對無源濾波器,有源濾波器的選址方法一般是算法優化選址,當可供APF接入的待選位置增加時,優化算法和綜合評估方法的計算量將成倍增加[13]。另一方面,上述文獻的優化模型大多考慮某一種指標或者依據決策者主觀因素決定目標函數的權重,實際上濾波器的安裝容量和諧波治理效果之間存在天然矛盾,因此綜合考慮濾波器的不同設計目標,得到滿足多目標模型的Pareto解集[14],采用基于模糊決策理論的多屬性決策技術,可以權衡安裝費用和治理效果之間的矛盾確定折中解方案,做到科學合理的決策。

從電壓總諧波畸變率、投資費用兩方面出發建立多目標優化模型,不僅滿足了系統治理效果,而且也沒有忽略經濟指標。因此,文中提出了一種基于靈敏度分析的有源電力濾波器多目標優化配置方法,能夠快速解決有源電力濾波器選址定容的問題。首先,建立了配電網諧波潮流計算模型,采用靈敏度分析方法,獲得安裝節點;其次,建立了考慮節點電壓總諧波畸變率和投資費用的濾波器容量優化模型;然后,基于分解多目標進化算法求解優化模型;最后,利用IEEE 18節點系統進行仿真驗證,結果表明了文章所提方法的有效性。

1 基于靈敏度分析的APF選址模型

對于網絡規模較大的配電網,通過智能算法計算APF的優化選址時,優化變量的維度會隨著節點數量的增長而增長,進一步導致計算量大,耗時長,配置方案經濟性差等問題。當注入的APF補償電流相同時,靈敏度分析法可以發現諧波電壓變化最敏感的節點,把諧波治理裝置安裝在這些節點上能有效改善諧波治理情況,它主要依據每一個節點安裝APF的靈敏度系數,選擇靈敏度系數比較大的節點為安裝備選節點,就能夠大大提高APF優化配置的效率。

1.1 配電網諧波潮流計算模型

諧波潮流計算是配電網諧波治理的基礎工作,是由基波潮流和諧波潮流兩部分構成[15]。進行配電網的諧波潮流計算,需要先根據線路、變壓器、發電機和負荷的數據,通過元件建模得到各元件的諧波數學模型和參數。

進而得到各次諧波下的諧波導納矩陣Yh;接著僅考慮基波分量進行潮流計算,求得各個節點的基波電壓;然后根據諧波源的注入電流,通過求解諧波節點電壓方程,得到各節點的各次諧波電壓。

諧波節點電壓方程可表示為：

(1)

式中IN,h為節點N上諧波源的第h次注入電流;UN,h為節點N的第h次電壓;N為配電網節點個數。

1.2 節點諧波電壓靈敏度分析

靈敏度系數是指以狀態變量表征的系統對于控制變量或擾動變量變化的敏感性程度[16-17]。靈敏度系數Sij體現了節點j的APF安裝容量對于節點i的電壓諧波畸變率敏感程度,它的值越大就表明在此節點安裝APF能有效改善諧波治理效果,所以根據靈敏度系數計算結果來選址是一種針對性強且效率高的配置方法。

配電網節點i的電壓諧波畸變率(total harmonic distortion, THD)的表達式為：

(2)

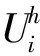
因此,靈敏度系數Sij可以定義為：

(3)

式中 Δαj為節點j的APF安裝容量。

由于THD和APF的容量之間并沒有直接函數聯系,文中的靈敏度計算通過諧波潮流計算完成,具體如下： 1)計算無APF時的配電網的THD;2)分別在每一個節點添加某小容量(文中Δα設為0.01)的APF得到此時配電網的THD;3)通過定義計算得到每個節點對應的靈敏度系數。靈敏度系數的計算流程見圖1。

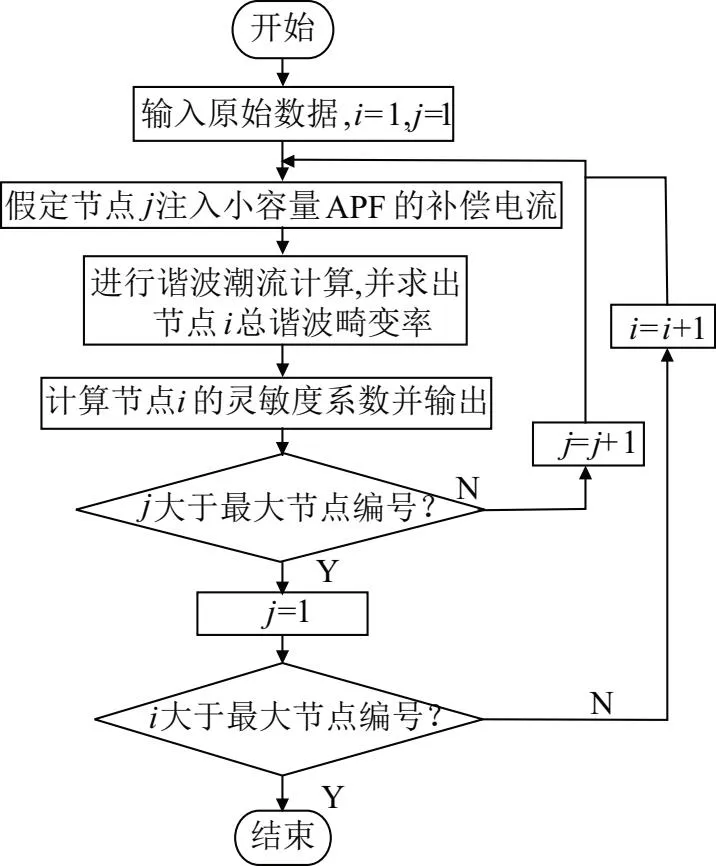
圖1 靈敏度系數的計算流程

所計算的靈敏度系數體現了節點對節點的影響關系,進一步,文中提出綜合靈敏度作為度量單個節點安裝APF對整個系統的影響指標。節點i的綜合靈敏度Sen,i可以定義為該節點靈敏度的相加,表達式為：

(4)

至此,根據綜合靈敏度系數的大小,對節點進行排序,選擇靈敏度大的前M個節點作為APF的安裝位置。

2 基于分解多目標進化算法的APF容量優化

通過靈敏度分析計算出APF的安裝位置后,需要進行APF容量優化配置。傳統的僅以諧波治理效果為單一目標的諧波治理裝置的研究,在實際工程應用中缺乏經濟性指標,因此選擇以諧波治理效果和經濟成本作為優化模型目標,可見APF容量優化是一個典型的多目標優化問題。分解多目標優化算法(multi-objective evolutionary algorithm based on decom-position,MOEA/D)是把多目標問題轉化為多個單目標問題,之后用數學規劃的方法求解,是如今求解多目標優化問題的新思路[18-19]。

2.1 優化模型

以電網平均電壓總諧波畸變率最小以及APF投資成本最小構建目標函數,表達式如下：

(5)

(6)

式中Ti為節點i投入的APF基礎安裝費用;Si為節點i投入的有源濾波器容量;KC為APF單位容量費用。

設由諧波源注入系統的諧波電流向量為：

Ih=[Ih,1,Ih,2,…,Ih,N]

(7)

APF通過檢測系統中的諧波電流繼而產生反向注入電流,實現諧波的濾除。設APF是依照一定的比例系數對諧波源產生的各次諧波電流進行吸收的,ahi為吸收系數,表示APF對節點i處的諧波源產生的第h次諧波電流的吸收率,因此系統中APF所補償的h次諧波電流用下式描述：

IAh=AhIh

(8)

Ah=diag[ah,1,ah,2,…,ah,N]

(9)

APF的容量僅取決于它所補償的各次諧波電流的有效值,計算過程如下：

(10)

式中H為最高諧波次數;Vh,i為i節點處h次電壓有效值;IAh,i為節點i處APF所補償的h次諧波電流有效值。

為了保證電網的安全運行,需要對電網的潮流進行安全性等式約束：

(11)

(12)

式中PG為發電機注入的有功功率;QG為注入的無功功率;PL,i為節點i上負荷消耗的有功功率,QL,i為消耗的無功功率;Vi、Vj為i和j節點的電壓幅值;Gij、Bij和δij各自為節點i和節點j之間的導納、電納以及相位差。

另外,諧波治理設備配置之后系統各個節點的諧波電壓含有率(HRU)和電壓總諧波畸變率都要達到國家標準GB/T 14549-93。

(13)

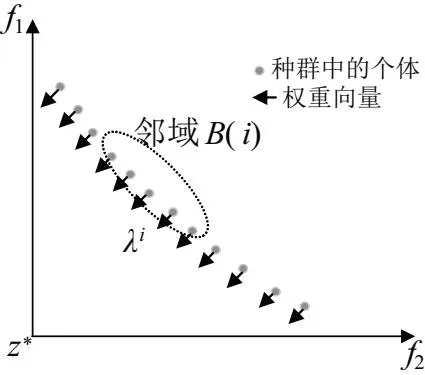
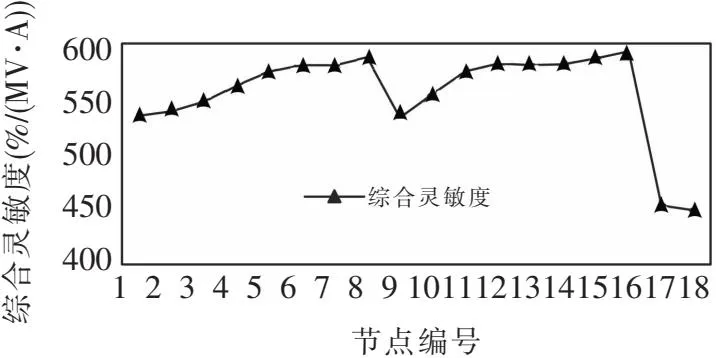
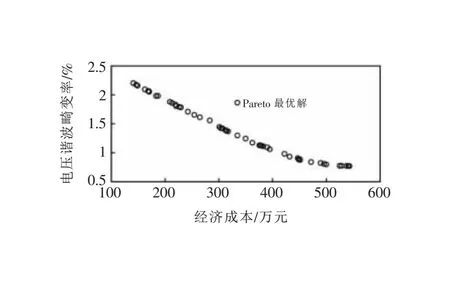
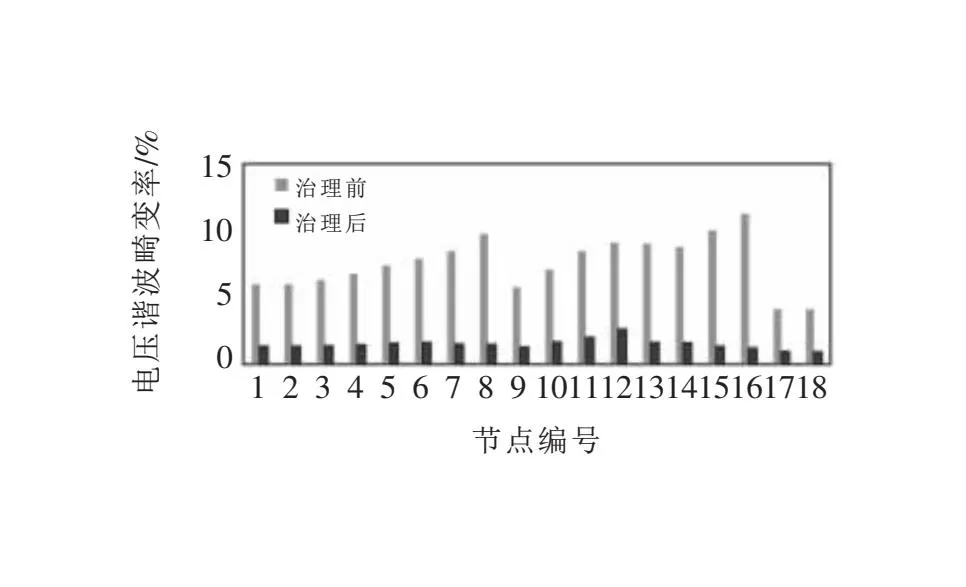
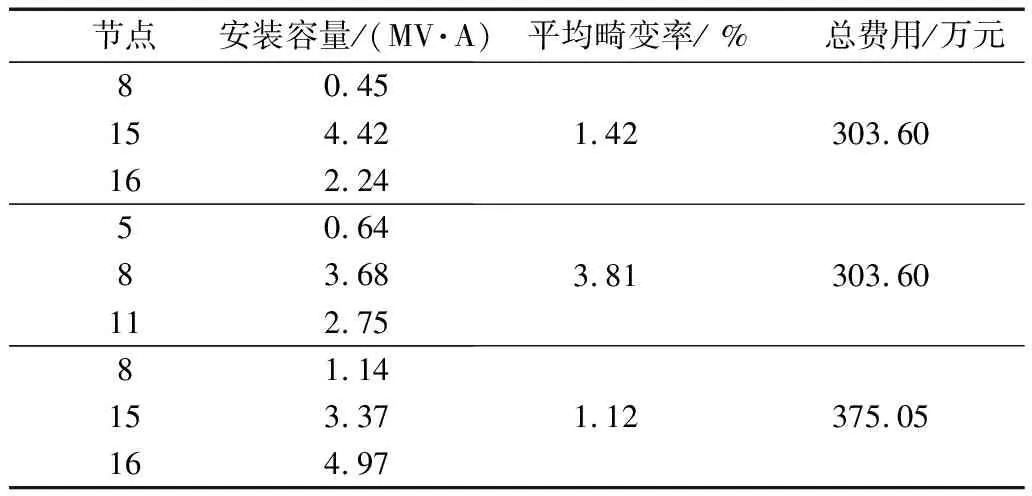
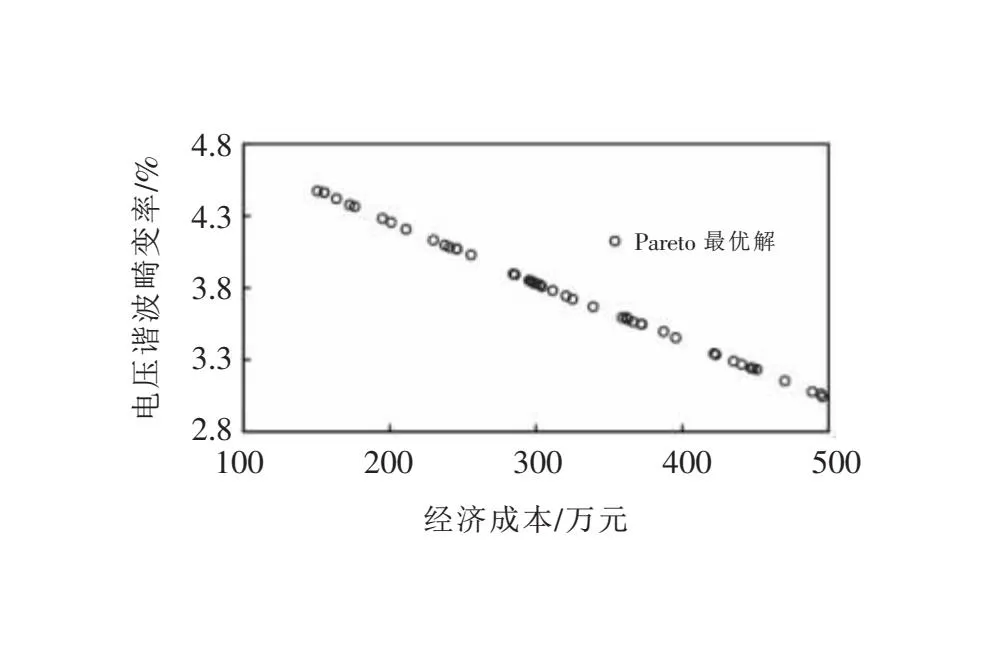
THDU

(14)

APF的開關容量是離散變量,需要滿足約束如下：

Simin≤Si≤uiSimax

(15)

Si=KS0

(16)

式中Si為在節點i處投入的有源濾波器安裝容量;Simin、Simax為節點i處能投入的最大和最小容量;K為整數;μi、S0分別為節點i處所投入的APF允許的過容量系數和單位容量。

2.2 求解方法

MOEA/D算法是把逼近求解多目標優化Pareto最優解集的問題,分解成若干個單個目標構成的優化標量子問題,然后每一個子問題都是使用相鄰問題的信息來協調優化的,保證了對最優解的挖掘并且計算復雜度有所降低。

如圖2所示,分解算法開始先把多目標優化問題在一定的權值方向上轉化為若干個單目標優化問題,以此來獲取整個Pareto前沿的逼近。

圖2 MOEA/D分解策略示意圖

文中選擇切比雪夫法分解策略,根據上文優化模型可知將電網電壓平均畸變率最小和APF投資成本兩個目標分解成m個子問題,該方法描述為：

(17)

(18)

如圖3所示,分解后的子問題要采用進化策略,按概率隨機在鄰域內挑選父代,再利用差分進化算子產生子代,確保算法搜索最佳解和保持多樣性的能力,以便有效覆蓋Pareto最優前沿。

圖3 MOEA/D進化策略示意圖

隨機從權重鄰域中取編號為r1、r2的兩個體,經過差分進化算子生成新個體y=(y1,y2,…,yn)。新個體的每一個分量yk表達為：

(19)

式中rand1、rand2都為隨機數,并且rand1∈[0,1],rand2∈{1,2,…,n};CR為變異率;F為控制進化的量化因子。隨后修改不合法的個體并更新參考點z=[z1,z2,…,zm]T和鄰域解,完成種群的更新。

針對諧波治理問題,由優化模型可知存在著等式約束和不等式約束,關于不等式約束需要增加懲罰函數來處理違反約束量,具體如下：

F(x)=f(x)+CP(x)

(20)

(21)

式中C為懲罰因子;P(x)為約束違反程度;gj(x)為各個不等式約束函數。僅當P(x)=0時存在可行解。

通過上述步驟得到Pareto最優前沿之后,決策者需要權衡經濟和治理效果指標,利用模糊理論從Pareto最優解中選擇一個作為最優折中解。采取以下隸屬度函數確定每一個非支配解對應目標函數的模糊關系：

(22)

式中Fimax、Fimin為Pareto最優前沿中第i個目標的最大值和最小值。

用標準化目標滿意度來衡量各最優解公式如下：

(23)

式中NP為最優解個數;m為目標函數的個數;折中解則是對應于μl中值最大的最優解。

3 算例分析

3.1 算例系統

文中采用IEEE 18節點的標準電網作為算例,網絡拓撲結構如圖4所示,有一臺發電機供電,一臺變壓器,9個電容器接地支路,以及15個負荷節點組成。仿真節點5、6、8、11、12、16處分別接入確定性諧波源,注入5次,7次,9次、11次、13次、15次諧波電流。選取整個系統的基準電壓為10 kV,基準容量為100 MV· A。算例的線路、負荷初始參數,諧波源節點注入電流情況參考文獻[20],所有數據均為標幺值。

圖4 IEEE 18節點系統拓撲圖

3.2 靈敏度分析

首先計算無APF接入時的配電網各個節點的THD;為了保證注入的補償電流相等需要在每一個節點都添加小容量為0.01 MV· A的APF,通過諧波潮流計算得出此時配電網的THD;最后,通過定義得出每一個節點的綜合靈敏度系數,所計算的綜合靈敏度結果見圖5。

圖5 綜合靈敏度結果

將各個節點根據綜合靈敏度系數大小排列順序,考慮經濟性因素選擇綜合靈敏度大的前M=3個節點作為APF的安裝位置。通過綜合靈敏度指標得到有源濾波器的安裝位置為節點8、節點15、節點16。

由于靈敏度分析法是首先獲得所需要安裝諧波治理裝置的節點,之后僅僅需要對容量進行優化求解相比將位置選取和容量優化都交給智能算法的統一配置方法,大大提高了計算效率。

3.3 多目標優化

基于MOEA/D算法得到了綜合考慮電網平均電壓總諧波畸變率最小和經濟成本最佳兩個優化目標的Pareto最優解前沿如圖6所示。可見采用文中所提方法安裝有源濾波器能有效達到諧波治理的效果,治理后的諧波畸變率都達到了國家標準要求范圍,投資費用也屬于合理接受范圍。

圖6 安裝位置為8,15,16時Pareto最優解

其中平均電壓總諧波畸變率最小和經濟成本最低為目標的單目標優化結果分別位于Pareto前沿的兩端。從結果可以看出,隨著經濟成本的升高,即有源濾波器安裝容量增加,電壓的總諧波畸變率將有所降低,反之亦然。

從Pareto解集中選取經濟成本為303.60萬元,電壓總諧波畸變率為1.42%時的最優解,與諧波治理前的諧波情況進行對比,結果如圖7所示。可見通過合理布置有源濾波器,各節點的電壓總諧波畸變率都有了大幅度下降。此時對應的有源濾波器的配置容量情況整理見表1。

圖7 諧波治理效果對比

表1 諧波治理指標

為了突出靈敏度分析的有效性,隨機將APF布置于存在諧波源的節點。當APF安裝在節點5、8和11時,通過MOEA/D算法求解Pareto最優解前沿見圖8。

圖8 安裝位置為5,8,11時Pareto最優解

可以看出花費303.60萬元左右安裝有源濾波器,電壓諧波畸變率才降至3.81%,雖然也滿足了國家標準不超過5%的要求,但是并沒有文中所提方法諧波治理效果好,因此可以驗證所提出的靈敏度分析法的有效性和準確性。

在綜合考慮兩個目標函數的情況下,計算Pareto最優解的標準化目標滿意度如圖9所示,并從中取折中解,其諧波治理效果指標及經濟性指標同分解進化算法選擇諧波源就地治理方式結果進行對比見表1。

圖9 標準化目標滿意度

表1中第一組數據和第二組數據是在相同經濟成本下選擇根據綜合靈敏度系數確定安裝位置和隨機選取諧波源位置就地治理的方案的數據對比情況,第三組數據是基于模糊決策求取折中解的數據情況。

經過對比結果發現文中優化方法在諧波治理效果指標及經濟性指標的表現都優于分散式諧波治理方式,并且優化算法的計算復雜度較低,運行時間少,因此更加證明了文中所提出的方法準確性和有效性。

4 結束語

非線性負載的廣泛使用,傳統的分散式的諧波治理方式存在一定弊端,治理效果不顯著或者經濟成本較高。文中針對上述問題給出了以下解決方案：

1)引入靈敏度分析法,根據綜合靈敏度大小,尋找靈敏度較大的點作為安裝APF的最佳地點,方法物理意義明確,治理效果好;

2)多目標優化配置設備的參數全面考慮了設備運行的經濟性、治理有效性以及各類約束條件,在保證有源濾波器安全可靠運行的前提下,協同優化能夠有效權衡諧波治理措施的經濟成本與治理效果,可以為有源濾波器的配置提供比較多的選擇方案。