電動汽車無線充電系統中彎道互感優化研究

駱強,胥飛

(上海電機學院 電氣學院,上海 201306)

0 引 言

如今隨著各國節能減排的政策號召和化石燃料減少的危機,世界各國都在大力推廣使用電動汽車,電動汽車的相關技術研究和開發也得到了專家學者、有關企業及國家的重視[1]。在電動汽車技術研發中,電動汽車的充電方式與續航能力至關重要。首先,傳統的插拔式充電存在著充電耗時長、電壓不穩定和接觸磨損等問題。其次,電動汽車的電池也存在著電能儲存不足,循環次數有限等問題。最后,擺脫冗雜的充電電纜的束縛的無線充電技術得到了大量的研究并且發展迅猛,在生活中也逐步得到推廣應用[2]。對于非接觸式的無線充電技術中,包括系統建模方法、參數配置及優化、頻率特性等方面關鍵技術[3-9],西南交通大學、美國橡樹嶺國家實驗室、中科院電工研究所、日本琦玉大學、麻省理工學院等科研機構均進行了研究。

充電技術研究中,長導軌式能量發射線圈由于具備系統成本低、電能變換裝置少等優勢而被廣泛選用[10]。但是該能量發射方式也存在著功率密度低,側移適應性弱,尤其在轉彎時電壓波動較大等問題。針對無線充電時轉彎的問題,文中設計了一種圓形補償線圈在轉彎時應用,可以減小能量拾取系統互感的波動,提高電動汽車動態中進行無線充電時電壓的穩定。接著,通過仿真的手段進一步優化、驗證補償線圈的設計。最后,通過實驗驗證了該彎道補償拾取系統獲取電壓的穩定性。

1 電動汽車無線供電系統轉彎互感分析

1.1 電動汽車無線供電系統轉彎過程

以日常生活中常見路段為例,在行駛中大多為90°彎道。由于文中選的是平坦彎道,所以不會產生汽車傾角,從而不考慮汽車傾角給電動汽車的充電效率帶來的影響。在不考慮彎道傾角的情況下,設置的平坦彎道選擇了四個彎道角度。基于模擬電動汽車行駛過程,汽車內部的拾取線圈與地面發射線圈為研究的主體,關注拾取與發射線圈之間互感耦合面積的變化與電能的變化。在此基礎上,簡述電動汽車在彎道時,其內部車載拾取系統與發射系統即彎道導軌之間的關系。如圖1所示,電動汽車無線供電系統主要分為：能量拾取系統、能量發射系統、信號檢測及控制端。

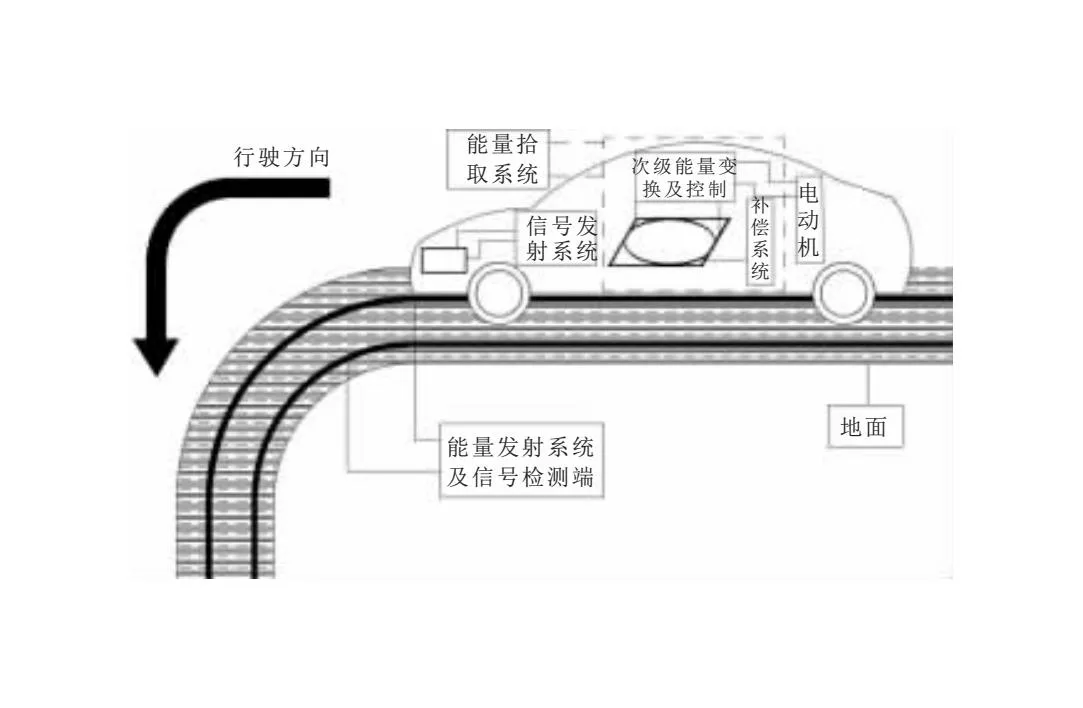
圖1 電動汽車行經彎道時系統結構圖

首先,電動汽車處于直道時,此時基于感應耦合原理,鋪設的發射線圈導軌和車載矩形拾取線圈實現了無線電能傳輸。接下來,電動汽車內部的能量變換即控制系統,經過一系列整流調控后,將滿足運行的能量輸入至電動機內,進而匹配汽車所需的運動要求。然后,電動汽車處于彎道時,此時原本運行到直道時地面發射線圈與汽車拾取線圈的互感在行進至彎道時發生了波動。這是由于在直道時汽車拾取線圈與地面發射線圈的正對耦合面積一直是穩定的,而進入彎道時拾取線圈和發射線圈間的正對耦合面積發生了變化,隨著彎道的駛入,正對耦合面積逐漸由大到小、再由小到大的變化,進而導致了互感變化,并導致電壓、電流的波動。因此,處于彎道時需要設計一個彎道補償系統以滿足穩定電壓、電流等電力指標的需求。最后,基于穩定的電力指標的要求,文中設計了彎道信號接收、發射裝置,汽車前端也設計了信號控制系統,一旦電動汽車處于彎道時,通過信號調控,便驅使彎道補償系統進入到工作狀態中。

1.2 彎道導軌和拾取線圈的設計

在電動汽車拾取線圈的選型中,大多數研究機構選擇的是矩形結構。相關研究表明,矩形線圈[11-12]作為拾取線圈,既可以實現經濟上便利和繞制簡單的優點,也可以保證拾取系統的效率高、偏移裕量多的特性。因此,將矩形線圈作為拾取系統的主接收線圈[13]。基于拾取線圈的選定,文中將提出彎道導軌的設計。文獻[14]指出,發射導軌、拾取線圈在保證拾取效率為80%以上,應當保證發射線圈的寬度要與拾取線圈的寬度近似相等,在長度方面,發射線圈要為拾取線圈的3倍以上,而兩線圈間的高度應遠遠小于兩線圈寬度與長度。由于文中所述彎道皆為單車道,因此也應當保證彎道之間的寬度即為兩線圈的寬度。基于以上設計分析可得如圖2所示的彎道導軌與矩形線圈尺寸設計圖。

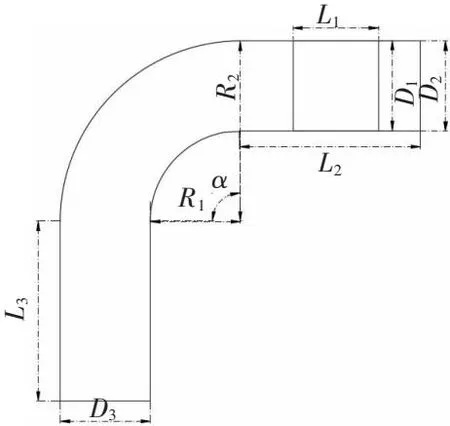
圖2 彎道導軌與矩形線圈尺寸設計圖

圖2中,L1、D1為矩形拾取線圈的長度與寬度,其匝數設為N1。發射導軌線圈在彎道前的直道上長、寬為L2與D2,彎道后的直道長度為L3,寬度為D3,而彎道中,彎道外徑為R2,內徑為R1,同時內外徑為同心圓,彎道角度為α。由于彎道為同一種線圈繞組而成,所以發射導軌匝數為N2。同時,發射導軌線圈與矩形拾取線圈間的耦合距離為h,即為垂直距離。根據上述分析,發射導軌與矩形線圈之間的尺寸關系如下：

(1)

1.3 彎道導軌尺寸與互感波動率關系

基于上節對彎道導軌與矩形拾取線圈的設定,文中將針對互感波動率、彎道內徑和寬度之間的比值Q=R1/D2、彎道角度的關系探究。COMSOL Multiphysics軟件為多物理場仿真軟件,尤其在對電磁耦合方面的建模與仿真的準確性,而被廣為應用。文中基于該軟件,對無補償的矩形線圈在彎道時互感波動進行分析。其仿真模型圖,如圖3所示。

圖3 90°彎道無線供電系統仿真圖

結合MATLAB軟件,經過多次仿真得出比例系數、彎道角度與互感波動率的擬合圖,如圖4所示。

從圖4所示的互感波動率與比例系數Q的擬合關系圖中,可以得到兩個結論：基于比例系數Q相同的彎道導軌,隨著彎道角度的增大,互感波動率也在增大;基于相同的彎道角度,隨著比例系數Q的增大,互感波動率在逐漸降低。

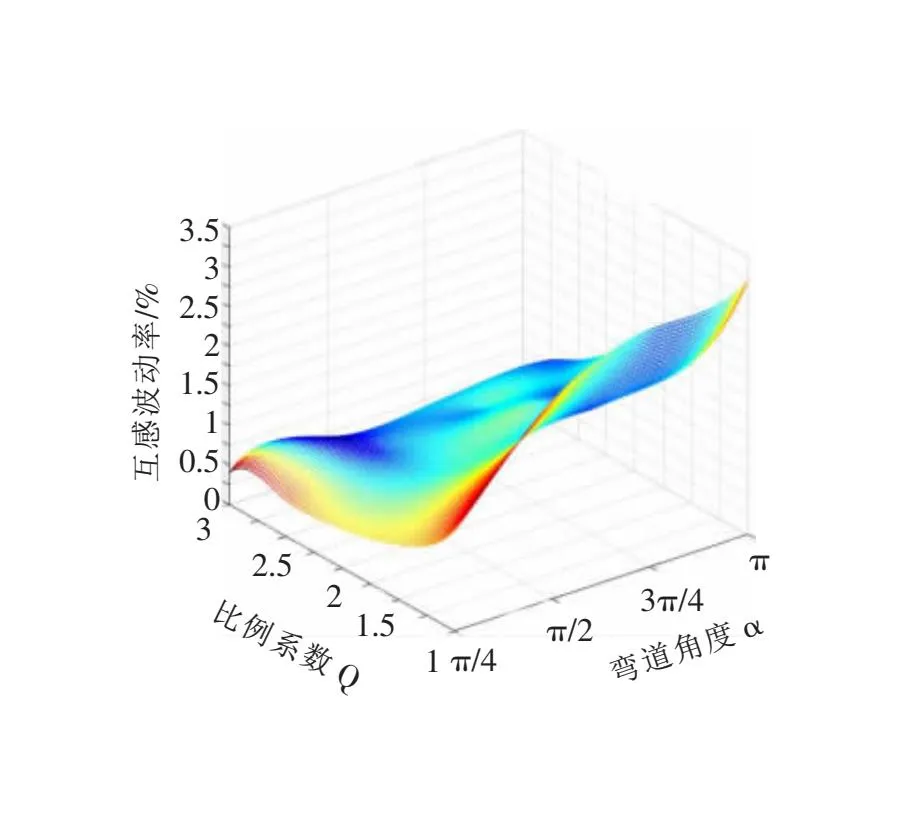
圖4 比例系數Q、彎道角度與互感波動率關系圖

基于對互感波動的原因分析,在直道時矩形拾取線圈與發射導軌線圈完全正對、重合,耦合面積達到最大,因此互感恒定。而當電動汽車無線供電系統中矩形拾取線圈經過彎道時,彎道處的發射線圈與矩形拾取線圈間無法如直道時完全重合,會有一部分矩形拾取線圈總是無法與發射導軌線圈耦合,因此會產生互感波動。進一步分析表明,當比例系數Q=3時,各角度互感波動率均保持在0.5%左右,這對于無線供電系統而言是足夠穩定的。在實際應用中,出于降低施工成本或減小土地占用面積等方面考慮,比例系數Q的范圍一般在1～2范圍內,此時各角度的互感波動率已經相對而言較大了,遠遠超過了互感波動率優化標準0.5%,如當比例系數Q=1時,基于尺寸參數設置,將相關參數設置到COMSOL中可得出四種彎道角度的互感波動率為1.37%、 2.62%、 3.15%、 3.47%,其互感波動率曲線圖如圖5所示。

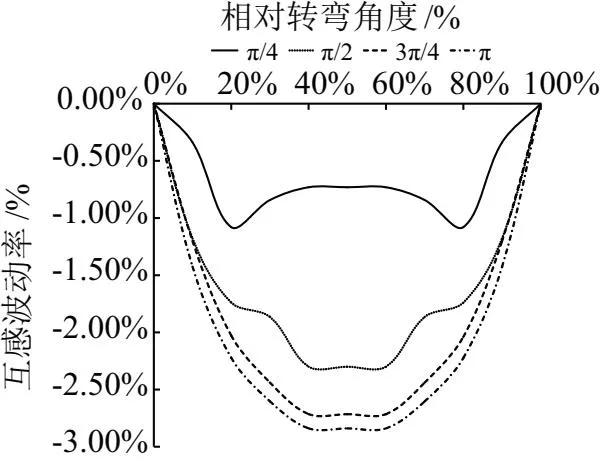
圖5 四種彎道角度下比例系數Q=1的互感波動率圖

由圖5可知,矩形拾取線圈在四種彎道導軌上的互感波動率已經達到了相當大的波動。因此,基于保持無線供電系統穩定性,對多角度彎道導軌進行補償顯得十分重要。接下來文中將以日常生活中較常見的比例系數Q=1的彎道,分析如何通過補償方法實現無線供電系統穩定性要求。

2 彎道補償拾取系統模型的構建和主要參數設計方法

2.1 補償線圈的選擇

基于上一節的敘述,矩形拾取線圈在四種彎道角度下的互感波動較大,因此,將對補償線圈的選擇以達到降低互感波動的目的。在無線供電系統中主要的補償線圈有矩形、圓形、六邊形線圈。文中采用的耦合線圈是基于彎道使用的,在文獻[15]指出對于三種補償線圈,圓形在彎道時有著較好的優勢,不僅可以保證互感的平穩,而且對于耦合系數及抗偏移能力上在三種線圈中都有著最好的表現。

為對比三種補償線圈的特性,文中使用COMSOL軟件進行互感仿真驗證,以選取在彎道中互感波動最低的線圈。首先,文中選取了相同匝數和面積的矩形、正六邊形、圓形線圈作為補償線圈,將其置于主拾取線圈上,同時設置了相同的物理環境與彎道及比例系數為1的導軌。基于以上仿真設置,結合MATLAB軟件得出三種線圈在相同角度彎道導軌轉彎下互感波動率變化曲線圖,如圖6所示。

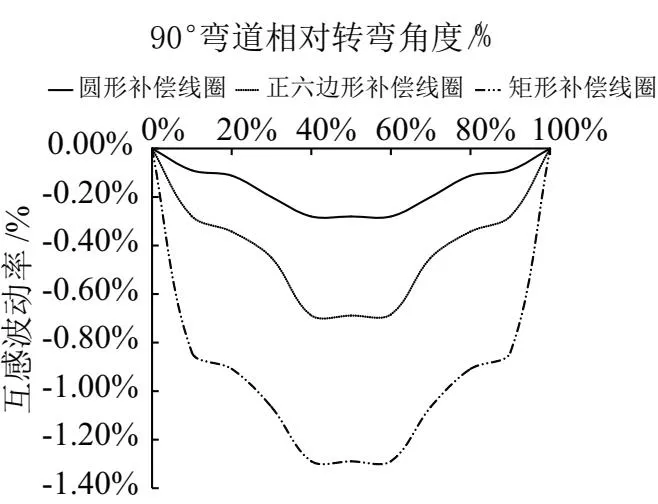
圖6 不同補償線圈在彎道上的互感值波動

由圖6可知,在主線圈為矩形拾取線圈下,加入的三種補償線圈均起到了降低互感波動的效果,這表明補償線圈是有必要的且也是有效果的。同時,通過三種線圈的補償效果可知,圓形線圈相比較于正六邊形與矩形線圈的互感波動是最低的,這是由于圓形補償線圈與發射線圈的互感耦合面積較小,并且進入彎道時,圓形補償線圈的嵌入位置完全處于發射線圈中,不會造成補償效果波動劇烈的情況。

基于以上分析,從互感波動的基礎上進一步仿真可知,在設置了相同的仿真匝數和彎道角度下,圓形的補償效果在彎道中一直要優于矩形、正六邊形線圈。因此,基于互感波動、抗偏移能力、耦合系數等方面考慮,文中選擇了圓形線圈作為補償線圈。結合以上論述,文中后面的彎道補償拾取系統為主拾取線圈為矩形,內嵌入一個圓形線圈作為補償線圈。在實際工程實踐中,將補償線圈置于矩形拾取線圈上方,當電動汽車欲駛入彎道時,原先置于上方的內嵌補償線圈通過切換線路并入到矩形拾取線圈系統中,使得彎道補償拾取系統開始工作。

2.2 彎道補償拾取系統模型的主要參數設計方法

結合圖2的能量傳輸系統尺寸圖,在添加前述的圓形補償線圈后,得到了圖7的彎道補償拾取系統尺寸圖。圖7中,內嵌入矩形拾取線圈的圓形補償線圈表示為r1,匝數為N,用于文中接下來的仿真、分析及實物平臺的搭建。

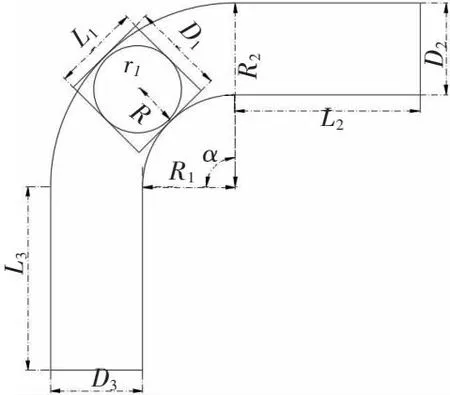
圖7 彎道補償拾取系統傳輸系統尺寸標識圖

如前所述,將圓形補償線圈的直徑設置為2R,且與主接收線圈的寬度相等,即2R=D1,其他尺寸參數與未補償的傳輸系統相同。同時,將圓形線圈與矩形線圈之間垂直距離設置為1 cm,在此距離下,文獻[14]指出補償線圈與拾取線圈間的互感比較與發射線圈間的產生的互感相比可以忽略不計。同時,由于拾取線圈與補償線圈均處于電動汽車內部的拾取系統中,通過同一的電能轉化裝置,可以將拾取線圈與補償線圈所獲得的電能轉化為驅動電動汽車所需要的動力。基于尺寸參數確定的前提下,彎道補償拾取系統中的補償線圈的匝數對于維持互感穩定起著決定性作用,因此將探究如何取得合適的匝數以確保互感波動在優化標準±0.5%的互感波動率范圍內。

由Neuman公式及耦合線圈之間的互感求解方法[16],得出了直道處矩形線圈與發射導軌的互感近似值M1,彎道處的互感近似值M2,圓形線圈于彎道處的互感近似值M3：

(2)

(3)

(4)

式中G(L1,L2,D1,D2,h)、H(L1,L2,R1,R2,h,α)、F(R,R1,R2,h,α)為尺寸參數。基于無線供電系統的穩定性要求與文獻[16]中指出線圈間總互感可以簡化為相互疊加的原理,因此系統內部的車載線圈與發射導軌之間的互感應為相等的關系,可以得出：M1=M2+M3。經過數學推導,可以得出系統穩定性的最優匝數比ζ0為：

(5)

互感(M1、M2、M3)由無線供電系統的實際需要選擇,進而可以得出三個互感值[17]。從以上的互感公式中可以得出,最優匝數在主拾取線圈已知的情況下,通過最優匝數比便可得出圓形補償線圈的匝數N。

3 基于遺傳算法優化及COMSOL仿真驗證

3.1 遺傳算法優化

基于互感近似值的求解,文中選用了遺傳算法以求得各角度彎道導軌下彎道補償拾取系統中最優匝數比ζ0。遺傳算法是依照以孟德爾的遺傳學說和達爾文的自然選擇為基礎的算法,文中基于文獻[14]的基本參數設置,通過彎道角度與最優補償匝數比ζ0的問題進行了研究。其優化目標函數如下：

(6)

文中使用的目標函數的約束條件為彎道角度α,其范圍為0≤α≤π。基于MATLAB軟件,文中編寫了遺傳算法,相關設置為：種群規模為1 000,交叉概率為0.92,變異概率為0.1,最大進化代數為500。文中通過不斷迭代的最優化匝數比與彎道角度的關系,經過了434次迭代后,目標函數趨于穩定。在此基礎上,文中通過遺傳算法優化的目標趨勢結合彎道角度的動態變化,得出了趨勢圖,如圖8所示。

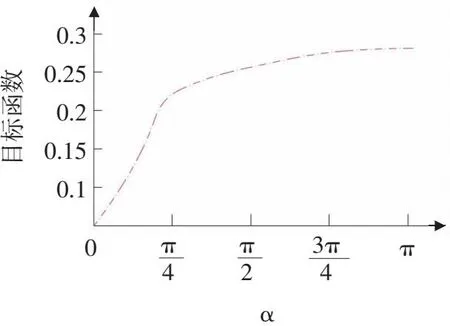
圖8 目標函數與彎道角度趨勢圖

圖8表明,隨著彎道角度的增大,目標函數即最優匝數比也在逐漸增大,但同時增大的趨勢開始降低,趨于平緩。文中結合常見的彎道角度：45°、90°、135°、180°,經過計算得出四種彎道角度的最優匝數N整數解近似值分別為：8、9、10、11匝。將其帶入互感公式中,經過MATLAB的處理,得出常見彎道角度補償最優匝數的互感波動率圖,如圖9所示。

圖9 常見彎道角度的最優化補償匝數互感波動率圖

根據圖9所示,四種彎道角度的最優補償匝數的互感波動率均保持在±0.5%范圍內,證明了基于遺傳算法優化的最優補償匝數比是可行的和有效的。為了進一步探究最優匝數下無線供電系統的互感波動率,文中接下來將使用COMSOL仿真軟件進行仿真驗證。

3.2 COMSOL仿真模型搭建與驗證

基于遺傳算法優化的最優補償匝數,文中使用了電磁仿真軟件進行驗證,四種彎道角度對應的最優補償匝數能否保持互感波動率在±0.5%范圍內。首先,基于第2節中尺寸參數關系,文中搭建了如表1所示的無線供電系統主要參數尺寸表,且在仿真及實驗中,設Q=1,h=20 cm。

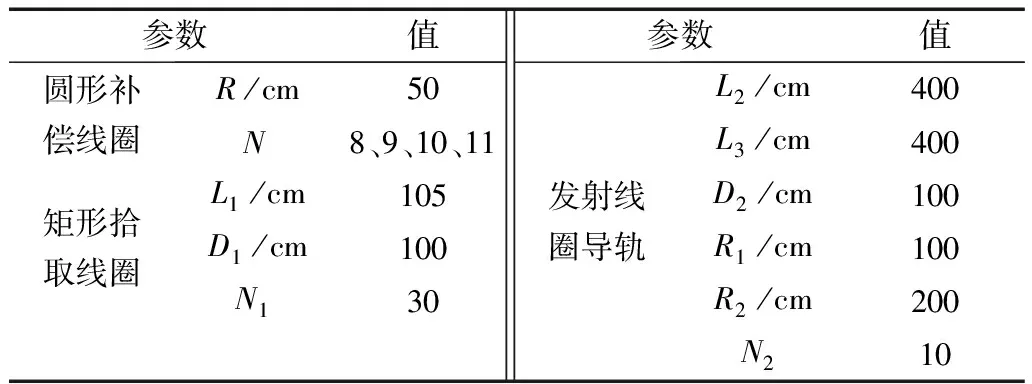
表1 無線供電系統主要參數尺寸表

結合以上參數,對COMSOL仿真軟件進行相關設置,對最優補償匝數的優化,對四種角度彎道仿真了四組匝數為：8、9、10、11。通過以上設置,得出圖10所示的互感波動率趨勢圖。

由圖10可知,彎道補償拾取系統在四種彎道角度導軌下,互感波動率相比于圖5的未補償的矩形拾取線圈已經大幅度降低了,表明了該設計的仿真可行性,也說明了彎道補償拾取系統對于任意角度彎道都有著保持互感波動穩定的效果。進一步分析表明,在圖10(b)、圖10(c)中可以得出,90°彎道的補償線圈匝數為9匝、10匝時,補償效果是不同的。其中,9匝時的補償效果是部分欠補償狀態,而10匝時補償效果為部分過補償,這表明了在計算補償匝數時,補償系統的理論推導出的最優補償匝數存在非整數的情況。同時,經過對比可知,通過遺傳算法優化的最優補償匝數與經過仿真實驗的匝數基本一致,表明了遺傳算法對最優匝數比及最優補償匝數的優化的準確性。

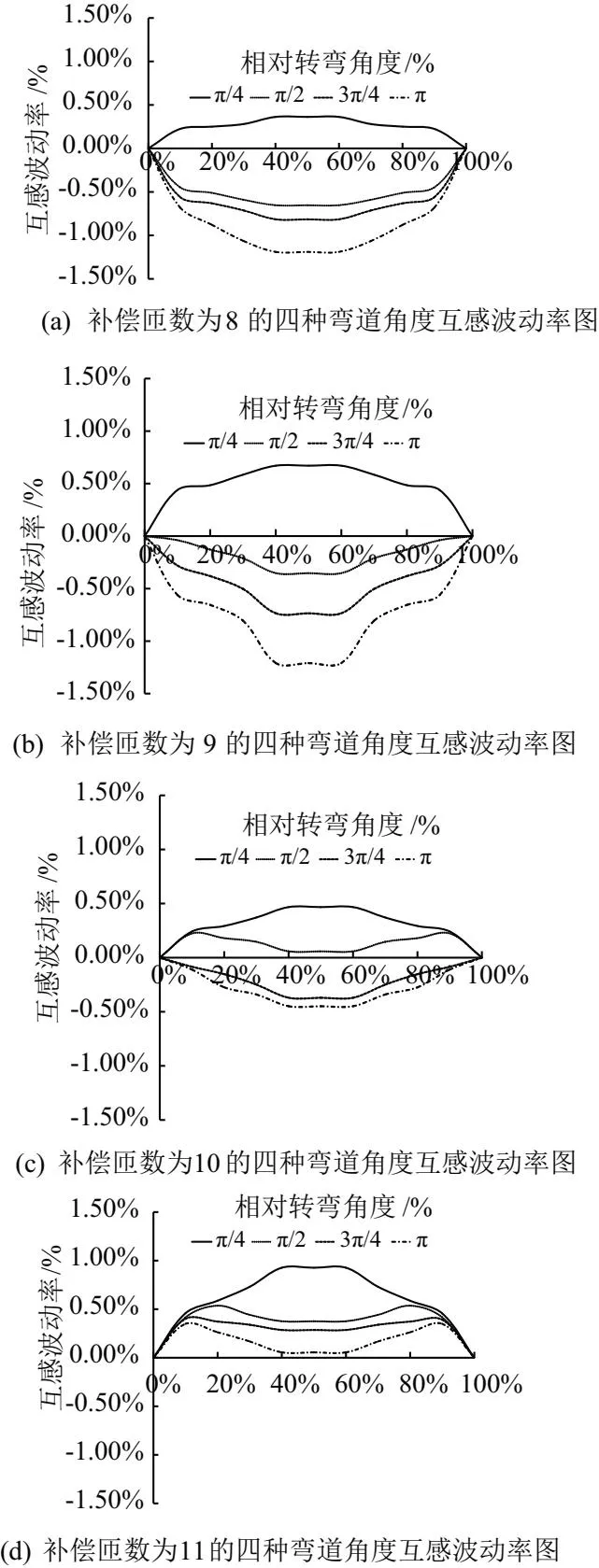
圖10 彎道補償拾取系統匝數互感波動率圖

在實際工程的應用中,我們只能選擇一個固定的匝數,并用于各種彎道的補償。根據上述對比,文中選擇了以N=10匝最為統一最優補償匝數,此時四種彎道角度導軌下互感波動率絕對值分別為：0.46%、0.28%、0.27%、0.44%,從而實現拾取系統在轉彎時互感的平穩。

經過上述論述,文中采取了遺傳算法優化與仿真驗證,都表明了文中設計的彎道補償拾取系統可以實現降低互感波動的目的。進一步研究表明,在統一最優補償匝數N=10下,通過四種彎道角度導軌的彎道補償拾取系統,互感波動率均在±0.5%范圍內,驗證了該設計的科學性與有效性。

3.3 統一規格下彎道補償拾取系統對電能傳輸效率的仿真

基于上節的論述,文中選擇最優匝數比ζ0=N/N1=10/30=0.3,即10匝作為統一的補償線圈匝數,并將表1參數設置使用到COMSOL軟件中,圖11為統一補償匝數下未補償的磁通密度與磁通強度分布圖。

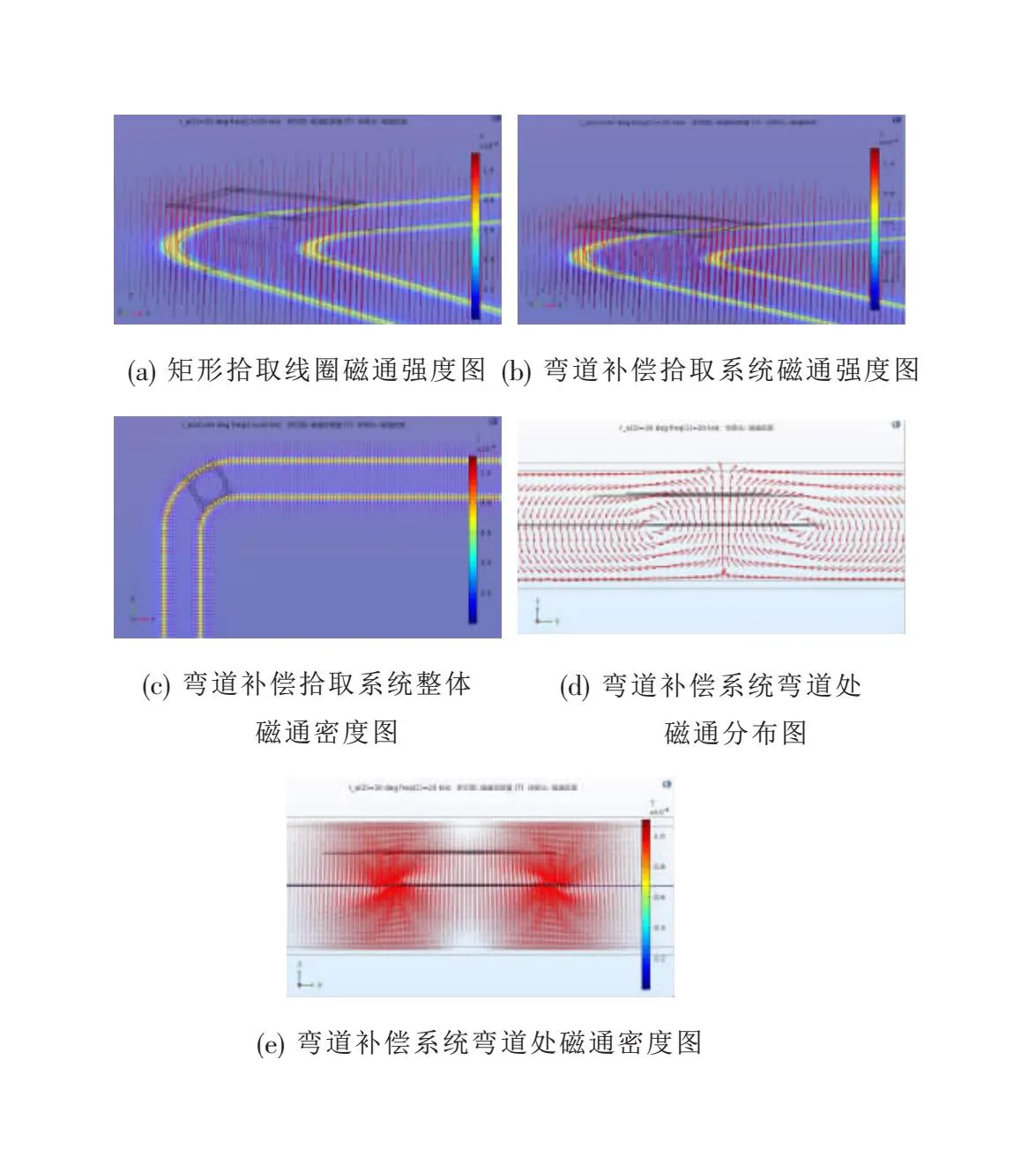
圖11 90°彎道電能發射線圈磁通強度與磁通密度圖

圖11(a)、圖11(b)表明,彎道補償拾取系統相較于未補償的磁通強度有著明顯的提高,起到了增強互感的作用。同時,由圖11(c)可知,彎道補償拾取系統的整體磁通強度分布均衡,表明了彎道補償拾取系統與整個發射導軌的互感穩定且波動很小。由圖11(d)、圖11(e)表明,彎道補償拾取系統在彎道處的磁通密度呈現了較為密集的情況,也證實了彎道補償拾取系統的設計達到了在彎道處補償的效果。因此,通過以上仿真、算法驗證了該設計的有效性與可行性。

3.4 電動汽車高度與無線充電效率關系仿真

基于上述參數設定,文中對電動汽車高度與無線充電效率進行了仿真探究。通過對彎道補償拾取系統的氣隙高度多次調整,結合COMSOL、MATLAB平臺得出了充電效率與氣隙高度、彎道角度的擬合圖,如圖12所示。

圖12 四種彎道角度下的充電效率與高度擬合圖

由圖12可知,當電動汽車處于20 cm處,充電效率最高。由于高度太低,拾取線圈與發射線圈之間存在電磁擾動,從而導致效率較低。同時,圖12中表明當汽車高度高于20 cm時,隨著高度的增加,充電效率在逐漸降低。因此,文中選擇的20 cm的高度既符合了充電效率的高要求,也滿足了汽車工程設計。

3.5 實驗平臺的搭建與驗證

在無線充電系統中,能量拾取線圈感應產生的開路電壓Voc與線圈之間的互感M存在如下的關系[18]：

(7)

式(7)中,能量拾取系統獲取磁通密度為B;IP為能量發射線圈電流;ω為系統工作角頻率;S為設計機構的有效耦合面積。根據式(7)知,基于其他條件已知情況下,互感M與能量拾取系統可拾取電壓存在正相關關系,穩定的互感對于電動汽車的能量拾取系統中的電壓穩定十分關鍵。因此,文中基于COMSOL的仿真設置,將發射線圈接入電流,將拾取系統中補償和拾取線圈接入同一輸出電能的設備,進而表現互感與電壓之間關系。

基于統一規格下各參數的設定,文中搭建了一套工作頻率為20 kHz的系統實驗平臺,由逆變電路、整流電路、SPP補償機構、電磁耦合機構、圓形補償線圈及負載等組成,其結構參數為：輸出功率3 kW,輸入電壓為交流380 V,逆變采用三相橋式逆變電路,用120°導通橫向換流方式控制[19]。整流采用了三相工頻整流電路,功率二級管為560V/52A,型號為SPW52N50C3。基于以上設置,文中將實驗數據進行整理,如表2所示。

表2表明了在20 cm處,無線充電的效率、互感、電壓均達到了理想的效果,從而證明了經過仿真、算法優化后的實驗平臺裝置達到了預期的優化目標。彎道補償拾取系統模型實物圖見圖13(a)。彎道補償拾取系統接收到的電壓波動如圖13(b)所示。圖中電壓波動范圍在16 V左右,相較于穩壓情況下的220 V,彎道補償系統的電壓為204 V,電壓波動率為3.6%;仿真互感波動率由圖10(c)可知為0.28%,保持了電壓與互感的平穩性,達到了優化標準,驗證了可行性。

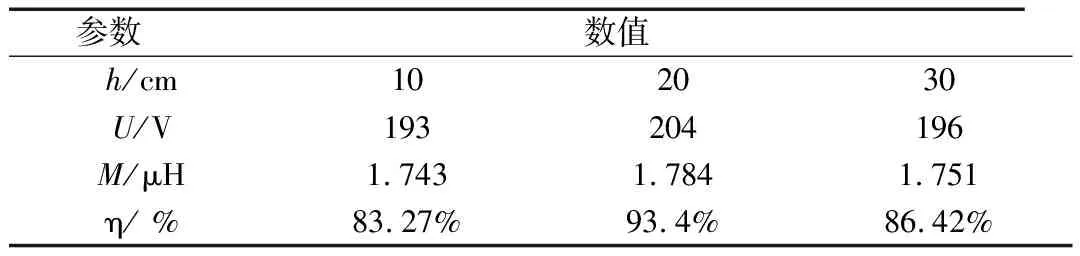
表2 基于20 kHz的實驗測量數據

圖13 實驗平臺與能量拾取電壓波形圖

4 結束語

文中以具有彎道的長導軌式電動汽車連續供電過程中,彎道處存在著互感波動和拾取端電壓下降的問題作為研究對象。首先,文中設定了彎道內徑與寬度的比值為比例系數Q,當Q=1～2時,通過仿真分析可知,電動汽車在轉彎時存在著較大的互感下降的問題。同時,也得出了比例系數Q=3以上時,任意彎道角度的互感波動率保持為±0.5%,達到了優化的標準。其次,文中基于實際出發,研究了比例系數Q=1的互感波動情況,研究表明此時電動汽車處于彎道時互感波動較大。因此,文中選擇了比例系數Q=1的彎道設置比例時作為研究互感波動率、彎道角度之間的對象,并選擇了補償線圈,設計了彎道補償模型。文中設計的彎道補償拾取系統模型,通過理論結合算法計算出最優化補償匝數N,經過仿真的驗證,證實最優化補償的匝數實現了優化的標準,保持任意彎道角度下,互感波動率均在±0.5%內。最后,通過仿真、實物的驗證了在統一規格下,解決降低了互感與拾取電壓波動較大的問題,達到了優化的效果。