基于GA優化BP神經網絡的小電流接地故障選線方法

徐思旸,范劍英,丁強

(1.哈爾濱理工大學 測控技術與通信工程學院,哈爾濱 150080; 2.哈爾濱理工大學 測控技術與儀器黑龍江省高校重點實驗室, 哈爾濱 150080; 3.煙臺東方威思頓電氣有限公司,山東 煙臺 264000)

0 引 言

電力系統中主要的接地方式為中性點接地和中性點不接地兩種,其中中性點不接地方式一般用于電壓等級為6 kV～66 kV的電網中[1]。配電網發生單相接地故障時,接地電流為系統的電容電流,只會經接地電容形成小電流回路,因此也稱為小電流接地系統[2],而此時由于系統的接地電流較小,不會過度損壞設備和系統,短時間內不影響連續供電,且對人身安全危害不大,因此我國規定配電網在發生單相接地故障后可繼續運行1 h—2 h以防止用戶突然斷電而引起不必要損失。但隨著發生故障后時間的增加,故障可能會進一步擴大,造成兩點甚至多點接地故障,同時單相接地會引發其他兩相對地電壓升高為相電壓數倍,會對設備絕緣造成威脅,如不能及時處理,很有可能引發兩相短路,弧光放電,引起系統過電壓等現象。因此在配電網發生小電流單相接地故障時及時進行故障選線對維護配電網運行具有重大意義。

然而當配電網出現單相接地故障時,因其故障電流數值比負荷電流小得多,導致故障特征不明顯[3-4]。針對這一難題,學者提出眾多選線方法,根據故障信號種類可分為穩態量法、暫態量法及綜合判據選線法。基于穩態分量的選線方法如基波比幅比相法、零序有功功率法,由于在過補償狀態下故障線路與非故障線路電流方向一致[5],故障信號電氣量失去“唯一性”特征,使得選線難度較大[6-7]。配電網中由于故障線路的暫態故障特征較為明顯,故基于暫態信息的選線方法比穩態量法更為可靠[8],例如小波包法、五次諧波法等可提高選線能力,但由于單一的基于暫態分量選線算法抗干擾能力較差,受現場多種故障情況限制,導致選線精度不高。目前利用綜合選線判據的方法進行選線[9]成為配電網故障選線發展的趨勢,文獻[10]提出利用模糊理論進行故障選線,但該選線方法由于分類精度不高,區分樣本特征不明顯,難以滿足準確選線的要求。文獻[11]提出利用BP神經網絡進行故障選線,但由于選取故障特征量較少,且在樣本訓練時容易陷入局部最優點,易造成選線誤差。為優化基于多判據融合的綜合選線方法,依據文獻[12]中利用GA優化T-S模糊神經網絡的方法,將GA優化后的BP神經網絡引入小電流接地故障選線中,優化后的神經網絡,基于多種傳統選線方法,并利用快速傅里葉變換(FFT)和小波包變換(WPT)算法提取多種特征量的方法進行綜合選線,對故障選線的精度和魯棒性有所增強,可實現快速精確選線的目的。

1 GA-BP神經網絡故障選線原理

1.1 故障選線結構

文中基于暫態量法與穩態量法兩類中已有的幾種選線方法：小波包法、五次諧波法、基波比幅比相法和零序有功功率法,從零序電流信號中提取各特征量并計算各自的故障測度,GA-BP神經網絡基于四種故障測度數據進行訓練并輸出選線結果[13]。圖1為GA-BP神經網絡選線結構框圖。

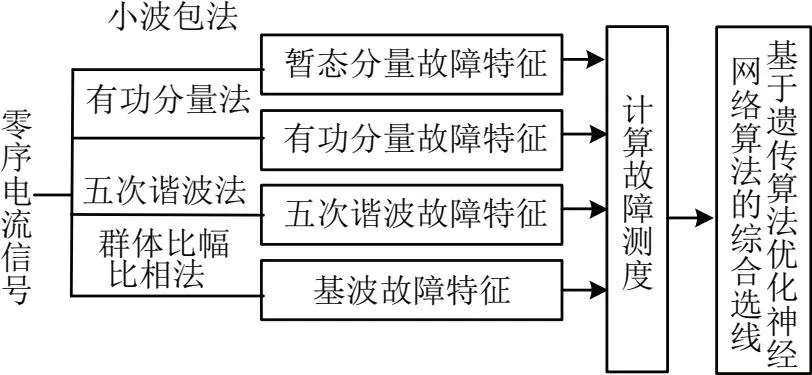
圖1 GA-BP神經網絡選線結構框圖

1.2 故障測度原理

文中定義閾值為[0,1]的故障測度函數見：

Xp(k)=Xrp(k)Xap(k)

(1)

式中Xrp為相對故障測度函數;Xap為可確定故障測度函數,故障測度值越接近“1”,其為故障線路可能性越大,反之越接近“0”,為非故障線路的可能性越大。

1.2.1 基于暫態分量的故障測度

設基于暫態分量的相對故障測度值為Xrp1,利用小波包法對暫態零序電流分析處理,選取高頻段信號,在特征頻段下,故障線路高頻段信號的能量較大且極性與其他電路相反。設配電網共有n條線路,線路k經小波包分解后特征頻段線路總能量之和為Ek,E為總線路的特征頻段能量總和,線路k的特征頻段線路總能量之和在所有線路中比重越大,其為故障線路的可能性越大。設計相對故障測度函數見：

(2)

基于以上原理,E/Ek比值越大,線路k為故障線路的可能性越大,利用該公式判斷故障線路可信度越高。設基于暫態分量的可確定故障測度值為Xap1,可確定故障測度函數如下所示：

(3)

1.2.2 基于有功分量的故障測度

設基于有功分量的相對故障測度值為Xrp2,利用零序有功功率法提取有功分量故障特征。當線路發生故障時,有功零序電流明顯增大且其極性與非故障線路相反。設共有n條線路,第k條線路中零序有功功率為Pk,無功功率為Qk,總線路有功功率之和為P∑。當Pk在P∑中比重越大時,其為故障線路可能性越大,反之越小。設計相對故障測度函數見：

(4)

Pk/Qk值越大,該方法判斷故障線路可信度越高,設基于暫態分量的可確定故障測度值為Xap2,由于小電流系統發生接地故障時,Pk/Qk比值結果相對較小,設因此定義可確定故障測度函數如式(5)所示,由于小電流系統發生接地故障時,Pk/Qk比值結果相對較小,式中?1=-4+lg2,?2=-2+lg2。

(5)

1.2.3 基于五次諧波的故障測度

設基于五次諧波的相對故障測度值為Xrp3,利用五次諧波法提取五次諧波分量。設共有n條線路,線路k中I05(k)為該線路五次諧波分量總和,I01(k)為該線路基波分量總和,I05為所有線路五次諧波分量之和。I05(k)在I05中的比重越大,線路k為故障線路可能性越大,反之越小,設計相對故障測度函數為：

(6)

I05(k)與I01(k)比值越大,即五次諧波分量在零序電流中比重越大,該方法判斷故障線路可信度越高。設基于五次諧波的可確定故障測度值為Xap3,定義可確定故障測度函數如式(7)所示,同上述有功分量可確定故障測度,式中?3=-4-lg4,?4=-1-lg4。

(7)

1.2.4 基于基波分量的故障測度

設基于基波分量的故障測度值為Xp4,利用基波比幅比相法提取零序電流基波分量,即基波分量特征值,線路發生單相接地故障時,其零序電流基波分量與非故障線路基波分量相位相反,且其幅值明顯大于非故障線路。設共有n條線路,線路k中I01(k)為該線路基波分量總和,I01為總線路基波分量之和。I01(k)與I01的比值越大,線路k為故障線路的可能性越大。定義故障測度函數如下所示：

(8)

2 GA-BP神經網絡原理

2.1 遺傳算法原理

遺傳算法模擬自然界中“優勝劣汰,適者生存”的叢林法則,形成一種隨機搜索最優化的方法。單一BP神經網絡在逆向反饋訓練樣本誤差的過程中是利用梯度下降算法來修正網絡的權重值和偏置值的,而該方法由于迭代公式固定以及誤差函數偏導數的限制,訓練誤差時容易得到局部最優解導致誤差偏大。而遺傳算法直接分析結構對象,沒有梯度下降算法中對參數求導和函數連續性的限制,由于其優秀的全局優化能力和并行性,沒有特定公式的限制便可以對優化后的參數空間進行操作并自適應地調整方向,可用于并行優化單一BP神經網絡。

遺傳算法將種群個體視為染色體,利用概率化尋優技術對樣本中經過編碼后形成的參數矩陣進行有效搜索。其中種群個體編碼、初代種群大小、適應度函數、迭代尋優設計以及控制參數設置構成了遺傳算法核心設計。遺傳算法運算過程如圖2所示。

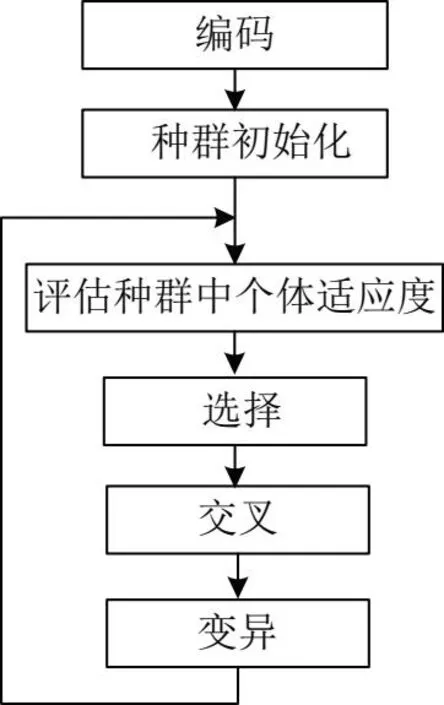
圖2 遺傳算法過程框圖

遺傳算法各運算步驟原理如下：

1)編碼。種群中每個個體都有其特有的特征,需要將這些特征記錄下來并轉換為遺傳算法可識別和操作的對象,即編碼。

2)種群初始化。即種群個體攜帶各層權值和偏置值并自定義種群規模。

3)評估種群中個體適應度,種群中每個個體都有其獨特的權值與偏置值,將個體的網絡輸出與期望輸出之間誤差作為個體適應度值。

(9)

式中F為個體適應度值;yi為網絡輸出值;oi為期望輸出值;k為參數;n為輸出個數。

4)選擇。文中隨機搜索個體的方法為輪盤賭選擇法。

fi=k/Fi

(10)

(11)

式中Fi為個體i的適應度;fi為Fi的倒數;fi越小,適應性越差;pi為個體i被選中的概率;fi越大,適應性越好,被選中的概率也就越大。

5)交叉。選擇的優秀個體組成新的種群,新種群之間進行“雜交”可以產生更優秀的基因。隨機選中兩個個體的兩個“基因”進行“雜交”。式(12)中akj、alj均為個體“基因”,b為參數。

(12)

6)變異。在遺傳學中,生物進化不止有交叉,還有“基因突變”。如式(13)、式(14)所示,r為0～1之間的隨機數,g為當前迭代次數,Gmax為最大迭代次數。

(13)

f(g)=r(1-g/Gmax)2

(14)

在算法形成初始種群后,遺傳算法用自適應迭代尋優的方法得到越來越優的近似解。通過類似于物種繁衍的組合、交叉和變異的遺傳操作,將適應度較大的個體組成代表新解集的種群,經過算法設定的最后一次迭代之后的種群適應度最大的個體即解碼后問題的近似最優解。

2.2 GA-BP神經網絡

BP神經網絡是一種多層前饋神經網絡,因其具有前向計算與誤差反向傳播的優點而得到廣泛應用。

圖3為神經網絡結構圖,x為網絡輸入,y為網絡輸出變量,文中利用已有選線方法提取的暫態分量、有功分量、五次諧波分量和基波分量故障測度值作為4組輸入變量,隱藏層設5個節點,輸出變量1個,代表選線結果。

BP算法在擬合非線性函數時,雖然可以收斂,但是有可能收斂到局部最小點,這是源于它的搜索是串行搜索,而遺傳算法的并行性,能夠使其更容易收斂到全局最小點。在遺傳算法優化神經網絡時,通過不斷的優化每一層的權值和偏置值,最終使網絡預測值不斷接近期望輸出,達到神經網絡準確預測結果的目的。而這個優化的過程,就是權值和偏置值不斷“進化”的過程,在每一次迭代過程中,權值與偏置值由于“自然環境”發生選擇、交叉、變異,然后留下更優的品種(權值和偏置值使輸出誤差最小),淘汰不好的品種,進而經過多次迭代,權值與偏置值的“基因”會越來越好,從而達到訓練目的。圖4為GA-BP算法程序流程圖。

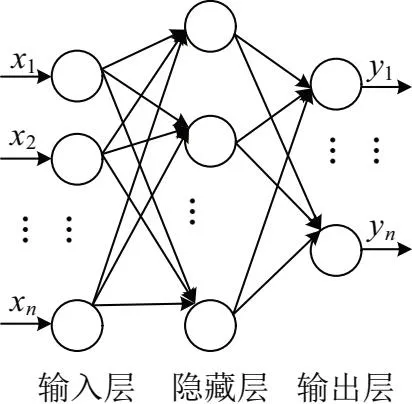
圖3 神經網絡結構圖

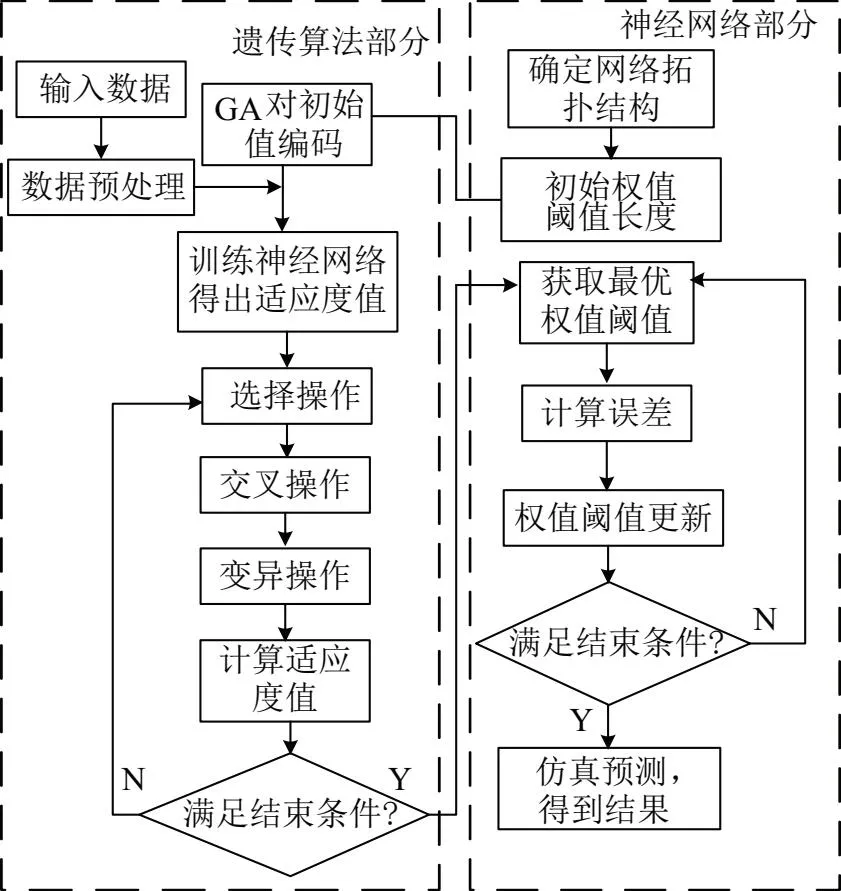
圖4 GA-BP算法程序流程圖

3 仿真建模與結果分析

基于MATLAB/Simulink環境對小電流接地系統進行建模和仿真,模型中共有4條10.5 kV的饋電線路。在現場工程中,為防止中性點經消弧線圈接地的小電流接地系統由于完全補償有可能引起串聯諧振過電壓,一般采取過補償的方式,在文中搭建仿真模型中,當過補償10%時,經計算消弧線圈電感L=0.8697 H,設置采樣時間為1.0×10-5s。

根據小電流接地系統建模,分別對不同線路4條,不同接地故障類型(金屬性接地、接地電阻10 Ω、接地電阻100 Ω),初始故障相角(0°、30°、60°、90°、120°、150°)及故障發生線路地點(10%、90%)設置發生單相接地故障,得到4×3×6×2=144組故障數據。對GA-BP算法具體參數進行設定,種群規模數10,最大迭代次數50,誤差精度目標為1.0×10-8,染色體長度為31,交叉概率為0.4,變異概率為0.2,BP神經網絡學習率為0.5。選取線路1在各故障情況下零序電流信號產生的故障測度數據為訓練樣本,樣本數為144。為體現基于GA-BP算法綜合選線的優越性,同時構建了4×5×1的單一BP神經網絡,以相同參數和訓練數據進行訓練。圖5為GA-BP神經網絡誤差訓練結果,在迭代3次后即可達到最優誤差精度1.6206×10-12。圖6為基于MATLAB/Simulink環境構建的單一BP神經網絡算法訓練結果,由圖6可知,在迭代50次后BP神經網絡不僅陷入局部最優解,而且誤差精度僅能達到6.5384×10-3。由此可判斷單一的BP神經網絡在訓練數據時需要迭代更多次且誤差精度較低,影響訓練效率,無法滿足小電流接地故障時快速選線的目的。

將線路4在各環境參數下的單相接地故障零序電流信號產生的144組故障測度值作為GA-BP神經網絡測試數據進行選線。分別選取基于小波包法、五次諧波法、基波比幅比相法、零序有功功率法提取的故障測度值及GA-BP神經網絡預測值作為仿真模型部分選線結果,如表1所示。判定故障測度值與GA-BP神經網絡預測輸出值大于0.5為故障線路,小于0.5為非故障線路。在仿真模型為金屬性接地,故障相角0°,故障位置10%條件下零序有功功率法與五次諧波法出現選線錯誤,在接地電阻100 Ω,故障相角30°,故障位置90%條件下,小波包法與基波比幅比相法出現選線錯誤。因此,單一的選線方法不一定滿足各種復雜情況下的準確選線,容易發生誤判,而在仿真模擬發生各類故障時,GA-BP神經網絡均可以準確快速地識別出故障線路且準確預測出與期望值接近的數值,選線正確率達到100%,滿足小電流接地系統故障選線對于快速、準確找到故障線路的要求。

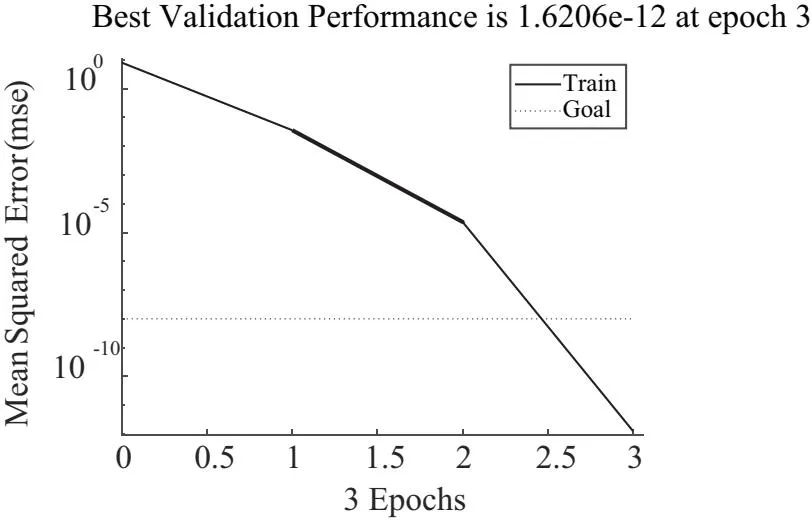
圖5 GA-BP神經網絡訓練誤差精度

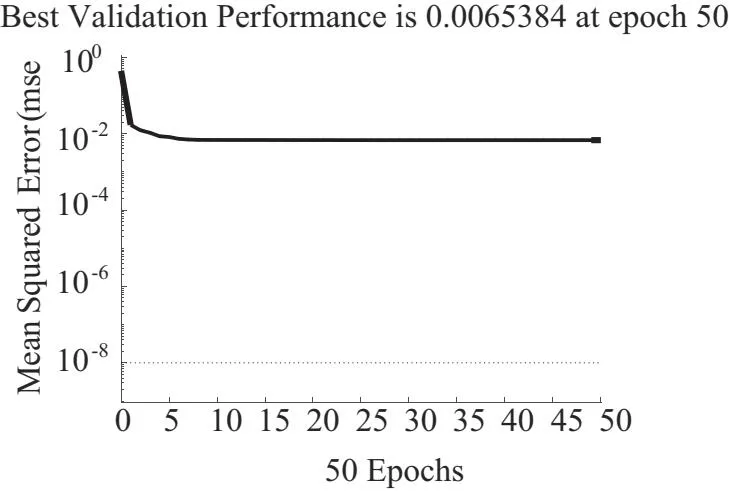
圖6 單一BP神經網絡訓練誤差精度

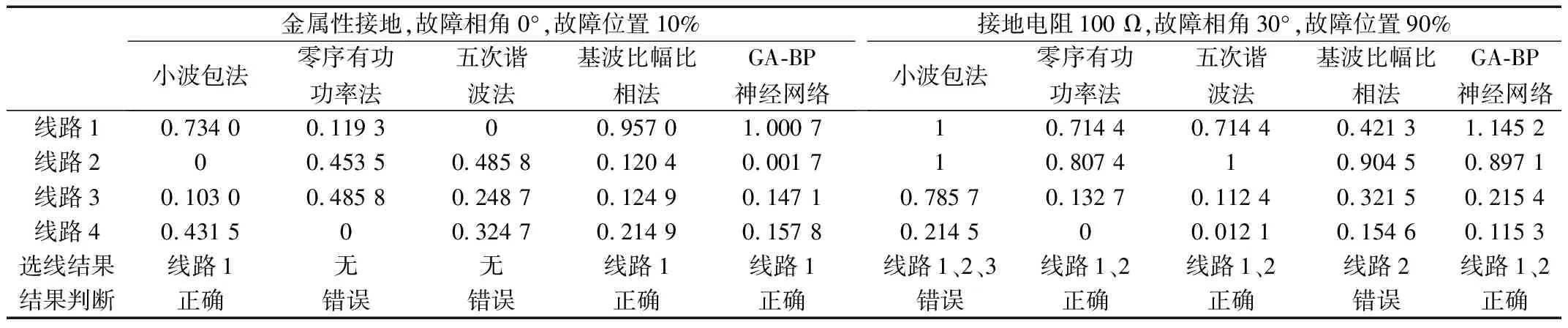
表1 仿真模型部分選線結果

4 結束語

文中利用小波包法、有功分量法、群體比幅比相法及五次諧波法等各種方法對零序電流信號進行處理,構建故障測度函數,消除在各故障情況下由于信號的干擾造成誤判的可能性。構建GA-BP神經網絡并基于四種故障測度數據進行網絡參數訓練,同時與單一BP神經網絡算法的選線性能進行比較,輸出GA-BP神經網絡選線測試結果并與四種傳統方法的故障測度值進行對比。結果表明,GA-BP算法的選線效率明顯優于單一BP神經網絡算法及四種單一選線方法。因此可初步得出結論,基于GA-BP神經網絡選線方法不受故障線路、故障類型、初始故障相角等情況影響,均能準確、快速地進行故障選線,對小電流接地系統基于暫態和穩態故障信息的融合選線有一定的參考價值。