慣量阻尼自適應虛擬直流發電機控制策略

王正男,張新慧,彭克,高震,程夢竹

(山東理工大學 電氣與電子工程學院, 山東 淄博 255000)

0 引 言

隨著能源短缺問題的日益嚴峻,新能源分布式發電技術成為國內外研究的熱點,與此同時,適用于分布式電源大規模接入的直流微網的研究也受到了廣泛的關注[1-2]。直流微網由儲能系統、分布式電源與負載等部分構成,與交流微網相比,直流微網無需考慮頻率、無功、相位等因素,供電質量更高。但在直流微網中,元件大多通過電力電子器件與母線相連接,致使直流微網成為了一個低慣性網絡,嚴重時會危害直流微網的安全穩定運行。針對此問題,模仿應用于交流微網中的虛擬同步發電機(virtual synchronous generator,VSG)控制策略[3-5],文獻[6]提出了能量路由器的概念,對交流變換器應用VSG控制策略,對直流變換器應用虛擬直流發電機(virtual DC generator,VDCG)控制策略,從而增強系統慣性。文獻[7-9]分別提出了VDCG控制策略在直流微網中光伏電源側、負荷側與儲能側的應用方式。以上對于VDCG控制策略的研究側重于不同變換器之間的應用,未考慮虛擬參數具有靈活調節的特性。文獻[10]通過引入母線電壓變化率,提出了一種慣量隨電壓變化率變化的自適應慣量阻尼控制策略,提升了其暫態性能;文獻[11]采用了具有限幅能力的反正切函數,根據功率波動、電壓幅值與電壓變化率對慣量阻尼進行了分層控制,通過對不同情況設置不同調節系數進行自適應控制。目前已有自適應VDCG控制策略均采用在母線電壓變化率前增加常系數調節量的控制方式,沒有考慮過母線電壓偏差對于系統慣性的需求,利用電壓變化率的常數倍進行慣性調節也未能充分發揮出虛擬參數調節的靈活性。

文中通過分析慣量阻尼在控制中的作用、擾動時母線電壓波動過程中系統運行狀況變化以及對慣性的需求,提出了一種附加動態調節系數的慣量阻尼自適應控制策略,可以更加靈活地調節系統慣性,減小功率波動帶來的影響。同時建立了應用該控制策略的直流微網小信號模型,利用阻抗比判據進行了小信號穩定性分析。最后利用PSCAD/EMTDC軟件進行建模仿真,驗證了所提控制策略的有效性。

1 虛擬直流發電機控制策略

VDCG控制策略是通過模擬直流發電機的機械方程與電氣方程,使變換器具有與直流發電機相似外特性的控制策略。直流發電機與DC/DC變換器VDCG控制策略的對應關系如圖1所示。

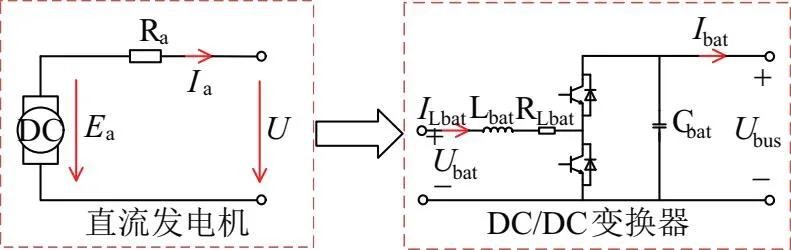
圖1 VDCM模型

VDCG數學模型如下所示。

機械方程：

(1)

(2)

式中J為轉動慣量;D為阻尼系數;Tm與Te分別為VDCG的機械轉矩與電磁轉矩;ω與ω0分別為VDCG的實際角速度與額定角速度;Pe為電磁功率。

電氣方程：

Ea=U+IaRa

(3)

Ea=CTΦω

(4)

式中Ea為電樞電動勢;U為機端電壓;Ia為電樞電流;Ra為等效電樞電阻;CT與Φ分別為轉矩系數與每極磁通。

在直流微網中,假設分布式電源輸出功率為0,則儲能系統所承擔的功率即為負載所消耗的功率與維持母線電壓偏差在允許范圍內所補償的功率之和。當直流微網中輸入輸出功率平衡時即可維持母線電壓的穩定。此時儲能系統所承擔的功率即為VDCG控制策略中的機械功率Pm。

儲能單元所承擔功率為：

(5)

式中Pbat為儲能單元所需承擔的功率;Ibat為雙向DC/DC變換器輸出電流;Uref與Ubus分別為母線參考電壓與實際母線電壓;Uload與Iload分別為負載電壓與負載電流。

根據式(1)～式(5),可得VDCG控制策略總體控制框圖如圖2所示。

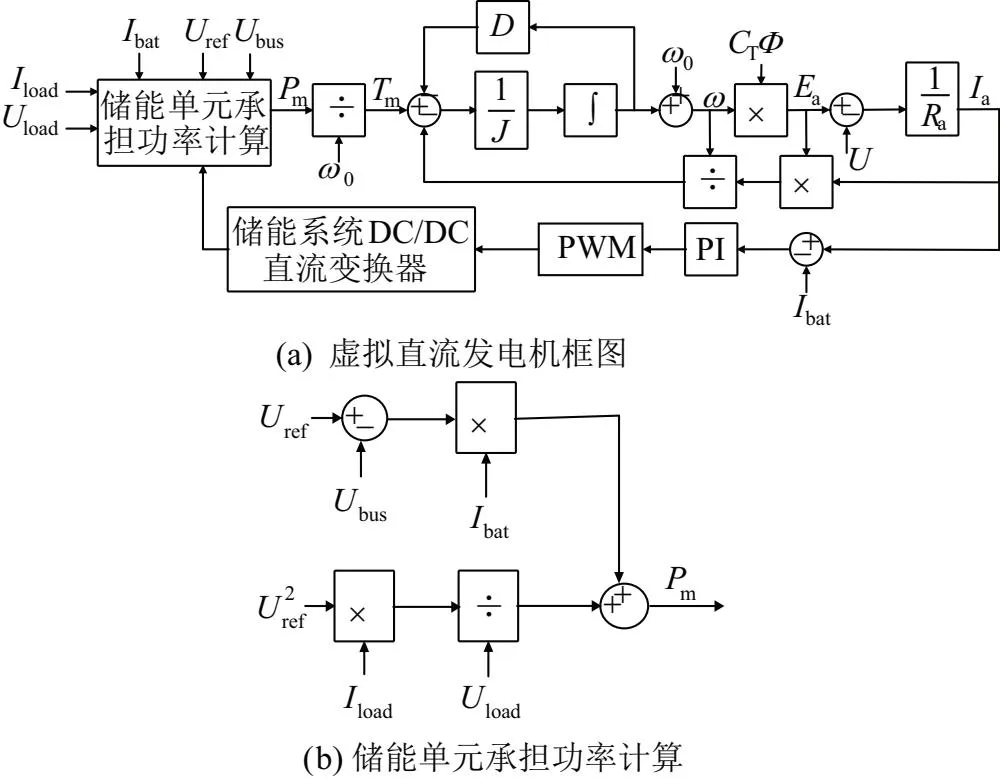
圖2 虛擬直流發電機雙向DC/DC變換器總體控制框圖

VDCG控制策略輸出的電樞電流Ia即為雙向DC/DC變換器的參考輸出電流。

2 慣量阻尼自適應控制策略

2.1 慣量阻尼參數分析

在直流微網中,儲能系統可根據系統功率缺額改變自身的輸出功率,以維持系統的功率平衡。VDCG控制策略對于雙向DC/DC變換器的控制體現在當系統發生功率波動,出現機械功率與電磁功率間的不平衡功率時,利用控制策略平滑地調節儲能系統的有功輸出功率,從而為直流微網系統增加慣性,達到抑制直流母線電壓突變的目的。

根據圖2(a)可得虛擬機械轉矩Tm至虛擬電動勢Ea的傳遞函數如式(6)所示：

(6)

由式(1)～式(4)可推得：

(7)

式中Pm=Tmω0為機械功率;Un為輸出電壓額定值;CT、Φ、Ra、ω0均為常數。

由式(6)、式(7)可知,VDCG控制策略相當于引入了一階慣性環節。當系統處于穩態時,電壓變化率為0,電壓穩定性取決于阻尼D,在輸出電壓不等于額定電壓時提供與電壓偏差值相關的阻尼轉矩,抑制由功率變化引起的電壓波動,起到減小電壓偏差的作用;當系統處于暫態時,J與D均會起到穩定電壓的作用,增大J可以在電壓變化率相同時產生更多的慣性轉矩,延緩系統的響應速度,抑制電壓波動。

綜上所述,增大J與D均會增大系統的慣性,減慢母線電壓恢復速度,給予系統更多的響應時間,從而在功率波動時起到抑制母線電壓波動的作用。

2.2 受擾動時母線電壓波動曲線分析

直流微網的穩定運行要求母線電壓具備較強的魯棒性,即：母線電壓變化時,應減小其變化的速度和幅值;母線電壓恢復時,應縮短其電壓恢復時間,使母線電壓的變化更加平滑。當直流微網功率波動時,母線電壓隨時間的變化曲線如圖3所示。

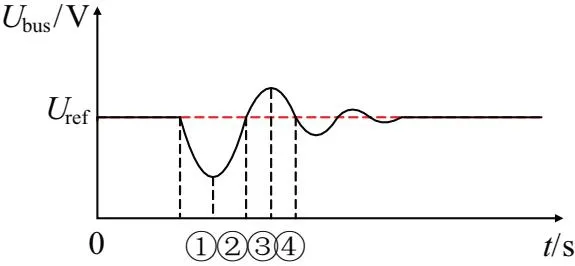
圖3 受擾動時母線電壓波動曲線

擾動時,母線電壓波動大致可分為①～④四個階段。當處于第①階段與第③階段時,電壓偏差ΔU=Ubus-Uref與電壓變化率du/dt同號,電壓偏差逐漸增大,為抑制電壓變化,應增大系統慣性,減小電壓波動幅度;當處于第②階段與第④階段時,電壓偏差與電壓變化率異號,電壓偏差逐漸減小,為加快母線電壓恢復速度,應減小系統慣性,縮短母線電壓恢復時間。在不同電壓波動階段下系統的運行狀態與對慣性的需求如表1所示。

表1 不同母線電壓波動階段系統慣性需求

2.3 慣量阻尼自適應控制策略

根據J、D參數分析與表1所示不同電壓波動階段下系統的運行狀態與對慣性的需求,提出了一種慣量阻尼自適應控制策略,其模型如下所示：

(8)

(9)

式中J0為穩態時的轉動慣量;a為慣量調節系數;Ja為J附加動態調節部分;Ju為J附加電壓調節部分;b為電壓調節系數;D0為穩態時的阻尼系數;Δd為阻尼調節系數;Du為D附加電壓調節部分;αJ、βJ、αd、βd分別為Ja與Du的底數系數與指數系數,αJ、αd取值應大于1;UdJ、UuJ與Udd分別為切換控制方式的電壓偏差上下限閾值,可根據國家標準供電電壓允許偏差規定進行選取。

如式(8)、式(9)所示,當|ΔU|小于UdJ或Udd時,為避免小干擾導致J、D頻繁波動,維持J、D為穩定值。

對于J的自適應,因J與Ja取值都不應過大,故在引入電壓變化率作為變量的方式上,采用具有限幅能力的反正切函數來構造方程。

1)當UdJ≤|ΔU|≤UuJ時,認為母線電壓處于理想范圍內,此時增大系統慣性主要用于抑制母線電壓的突變。引入Ja可以提高慣量調節的靈活性,減小αJ并增大βJ可以在電壓變化率較小時平緩增大慣量,減小對系統響應速度的影響,在電壓變化率較大時迅速增大慣量,抑制電壓變化趨勢,反之則可使慣量更平穩地變化。當電壓變化率趨近于0時,Ja趨近于1。

2)當|ΔU|>UuJ時,認為母線電壓已經超出理想范圍,但隨著電壓偏差增大,電壓變化率逐漸減小,系統慣性下降,會導致電壓偏差進一步增大。為避免電壓超出允許范圍,引入Ju,使J自適應可以根據電壓偏差動態調節,補償系統因電壓變化率減小而缺失的慣性,阻礙電壓的變化。當電壓偏差趨近于0時,Ju趨近于1。

對于D的自適應,根據分析可知,隨著D的增大,相同功率擾動引起的電壓偏差會減小,故當|ΔU|≥Udd時,引入Du作為Δd的修正量,可以在提高阻尼調節靈活性的同時,隨著電壓偏差變化動態調節D的大小,發揮D減小電壓偏差的作用。當電壓偏差趨近于0時,Du趨近于1。

3 小信號穩定性分析

為驗證應用慣量阻尼自適應VDCG控制下系統運行的穩定性以及慣量阻尼對于系統穩定運行的影響,建立附加儲能單元與負載的直流微網系統的小信號模型,并對其進行小信號穩定性分析。

如圖1所示雙向DC/DC變換器,設其占空比為d,建立雙向DC/DC變換器狀態空間方程,如下所示：

(10)

式中Lbat與RLbat分別為變換器的電感與電感寄生電阻;Cbat為變換器的輸出電容;iLbat與ibat分別為流過電感的電流與變換器的輸出電流;ubat與ubus分別為變換器輸入電壓與輸出電壓。

根據式(10)可推導得出雙向DC/DC變換器小信號動態特性,如式(11)所示：

(11)

式中Gduo為變換器占空比與輸出電壓之間的傳遞函數;Giil為變換器輸出電流與電感電流的傳遞函數;Zboo為變換器開環輸出阻抗。

根據圖2可推導出輸出電流到電樞電動勢的傳遞函數和電樞電動勢到電樞電流的傳遞函數分別如式(12)和式(13)所示：

(12)

(13)

儲能變換器小信號模型如圖4所示。

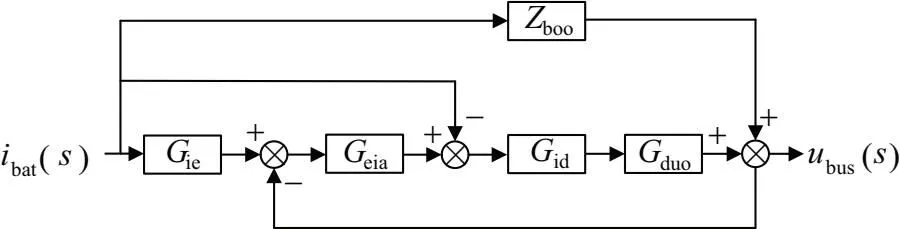
圖4 儲能變換器小信號模型

根據式(11)～式(13)與圖4可得控制策略下雙向DC/DC變換器的閉環輸出阻抗,如下所示：

(14)

式中Gid=kp+ki/s,為電流環傳遞函數;kp、ki分別為比例增益系數與積分時間常數。

假設負荷通過串聯電感與并聯電容與母線直接相連,則負荷輸入阻抗為：

(15)

式中Lload與Cload分別為濾波電感與濾波電容。

微源輸出阻抗即為儲能系統雙向DC/DC變換器的閉環輸出阻抗Zboc。

根據一種改進的阻抗比判據[12]可知,只要微源與負荷阻抗比Zboc/Zdoc的Nyquist曲線不進入禁止區即可保證系統小信號的穩定性。小信號模型的仿真參數如表2所示。

表2 小信號模型仿真參數

根據改進的阻抗比判據與仿真參數,可得到J、D的Nyquist曲線如圖5所示。

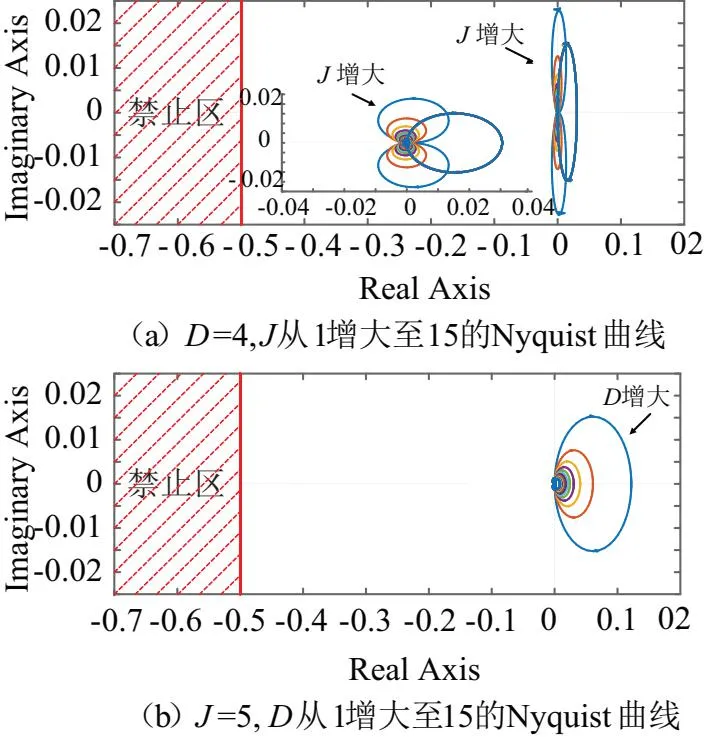
圖5 微網阻抗比Nyquist曲線圖

如圖5(a)所示,當D值恒定,逐步增大J時,Nyquist曲線圖左側部分向內收斂,右側部分幾乎沒有變化,可見增大J能夠使得Nyquist曲線逐步遠離禁止區,提高系統的穩定性。如圖5(b)所示,當J值恒定,逐步增大D時,Nyquist曲線左側部分幾乎不變,右側部分向內收斂,Nyquist曲線圖并沒有明顯遠離禁止區,可見增大D對于提高系統穩定性的影響不大。由圖5可知,無論調整J或者D,Nyquist曲線圖始終保持在禁止區外,說明在該取值下系統在穩態工作點附近能夠保證直流微網小信號穩定。

4 仿真結果與分析

為驗證慣量阻尼自適應VDCG控制策略的有效性,在PSCAD/EMTDC仿真軟件中進行仿真驗證,仿真參數如表2所示。選取J0= 5,a= 1.2,αJ= 2,βJ= 2.5,b=30,D0= 4,Δd= 1.5,αd= 1.2,βd= 0.5。

圖6所示為負載消耗功率,相同功率變化下慣量阻尼自適應VDCG控制策略與恒壓控制對母線電壓調節能力的對比如圖7所示。

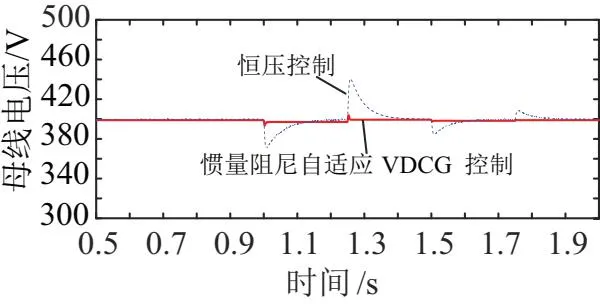
圖7 母線電壓波形

由圖7可知,在慣量阻尼自適應VDCG控制下母線電壓跌落幅度與電壓恢復時間均優于恒壓控制,表明該控制策略使系統獲得了慣性與阻尼,可以抑制負荷突變引起的母線電壓波動,維持微網穩定運行。

圖8為同在圖6所示功率擾動下,慣量阻尼自適應控制、J自適應控制、D自適應控制、傳統慣量阻尼恒定控制以及分別計及Ja、Ju、Du的電壓調節效果對比圖。

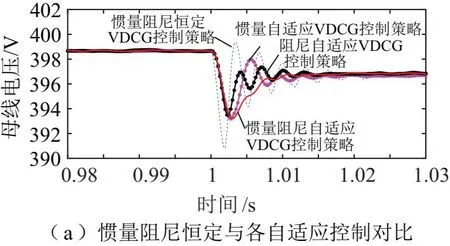
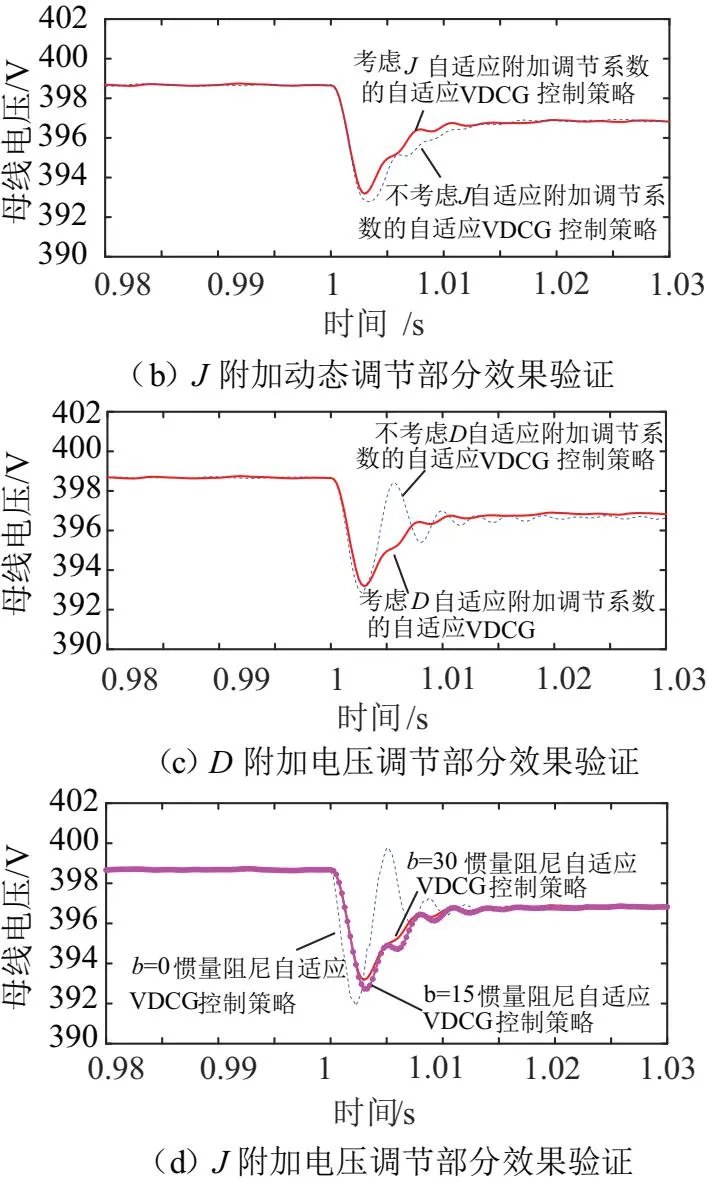
圖8 各控制方式電壓調節效果對比

由圖8(a)可知：

1)J自適應控制延緩了系統的響應速度,減少了電壓波動的次數與電壓波動幅度。說明J自適應控制可增大系統慣性,起到抑制母線電壓突變的作用。

2)相比J自適應控制,D自適應控制雖然不能減少電壓波動次數,但可進一步減小電壓波動幅度,縮短電壓恢復時間。說明D自適應控制在同功率擾動下可減小電壓偏差,對系統慣性的影響小于J自適應控制。

3)相比于其他三種控制方式,慣量阻尼自適應控制可使電壓更加平緩地達到新的穩態,幾乎沒有出現波動。說明慣量阻尼自適應控制能更好地根據系統運行狀態調節系統慣性,電壓調節效果更好。

由圖8(b)可知：考慮Ja可減小電壓跌落,提高電壓恢復速度。說明考慮Ja電壓調節效果更好。由圖8(c)可知：考慮Du可減小電壓波動幅度,使電壓的變化更加平緩。說明考慮Du可根據電壓偏差動態調節系統阻尼,減小電壓波動。由圖8(d)可知：隨著電壓調節系數b的增大,電壓跌落幅度減小。說明考慮Ju可以在電壓偏差增大時提高系統慣性,補償電壓變化率減小帶來的慣性損失,抑制電壓進一步下降。

綜上所述,相比傳統的恒定慣量阻尼控制,文中所提慣量阻尼自適應控制在同功率波動下具有更好的電壓調節效果,驗證了所提控制策略的有效性。

5 結束語

通過分析電壓波動各階段對于系統慣性的需求及轉動慣量J與阻尼系數D在虛擬直流發電機控制策略中的作用,文中提出了一種附加動態調節系數的慣量阻尼自適應控制策略,可以更好地反應系統運行狀態,提高控制的靈活性,減小功率波動對電壓的影響。同時建立了系統小信號模型,利用阻抗比判據分析了慣量阻尼對系統穩定性的影響。最后,利用PSCAD/EMTDC仿真軟件,對慣量阻尼自適應控制等多種控制方式進行仿真對比與分析,仿真結果驗證了所提慣量阻尼自適應控制策略的優越性。