研究教材習題 破解歷年真題
——以2019年人教A版教材必修第一冊58頁第5題為例

郭天總 馬靜輝 王紅波

(河北省邯鄲市永年區第二中學)

教材是教師教學、學生學習及備戰高考的最重要的資料,因為高考試題命制的一個原則是“源于課本,但高于課本”,所以高考命題很注重開發教材、研究教材,挖掘教材知識的考查價值和功能,許多高考試題所涉及的思想方法都源于對教材例、習題的深入研究.因此,在平時的教學與備考中要充分發揮教材的功能,從煩瑣的復習資料中跳出來,研讀教材,吸取營養,更好地培養學生的數學核心素養.下面作者就自己在研究教材、尋找通性通法、破解高考真題時的一些做法與大家分享、交流,希望能起到拋磚引玉的作用.

一、經典習題

(2019年人教A版必修第一冊58頁第5題)若a,b>0,且ab=a+b+3,求ab的范圍.

【分析】看問題:求ab的范圍.(屬于范圍問題)

想方法:(1)不等式思想;(2)函數思想;(3)數形結合思想;

看條件:a,b>0,ab=a+b+3;

定措施:

措施一:令ab=t(t>0),與ab=a+b+3聯立建立關于b(或a)的一元二次方程,根據方程有正根建立關于t的不等式求解.

【解析】法一:由已知得a+b=ab-3,

換元

代入ab=a+b+3,

整理得b2+(3-t)b+t=0,

聯立

因為該方程有正根,

列式

求解

所以ab的范圍為[9,+∞).

二、方法梳理

雖然上述習題可用三種方法來解決,但這三種方法中,法一、法二是常用的通性通法.通過對法二的解題過程進行梳理,可以總結出這種方法的基本步驟為:換元、聯立、列式、求解.其中的換元即把所求的g(a,b)看成一個整體t,聯立是把g(a,b)=t與題設中已知的等量關系聯立之后,構造一個一元二次方程,列式是根據方程有根(或有正根),列出關于t的不等式,通過解不等式達到求范圍的目的.這樣的歸納總結,可以培養學生的程序性思維,提高學生分析問題和解決問題的能力,提高學生的邏輯推理素養.

教師在教學中若能更多地注重“多題歸一”(所謂“一”就是具有普遍意義和廣泛遷移性的、“含金量”較高的解題方法與策略),更多地注重思考題目的“核心”是什么,從題目中“提煉”反映數學本質的東西,掌握好解決數學基本問題的通性通法,這樣才能達到學生會一道,通一片的教學目的,起到事半功倍的教學效果.

三、破解真題

“2019年人教A版必修第一冊58頁第5題:若a,b>0,且ab=a+b+3,求ab的范圍.”這是一道雙變量的求范圍問題,此題既可配湊出定值利用基本不等式或其變形求解,也可通過換元法,轉化為一元二次方程根的分布來求解.本習題中的條件ab=a+b+3是個很好的情景,該情景可以通過圓、解三角形、橢圓等知識點來呈現,因此以此題為依據擴展出來的高考題目有很多,列舉如下:

【真題1】[2023年高考全國乙卷數學(文)第11題]已知實數x,y滿足x2+y2-4x-2y-4=0,則x-y的最大值是

( )

【答案】C

【解析】法一:令x-y=t,則x=t+y,

換元

代入原式化簡得

2y2+(2t-6)y+t2-4t-4=0,

聯立

因為存在實數y,則Δ≥0,

即(2t-6)2-4×2(t2-4t-4)≥0,

列式

化簡得t2-2t-17≤0,

求解

法二:由a2+b2≥2ab(a,b∈R)得

由已知得(x-2)2+(y-1)2=9,

【真題2】(2022·新高考Ⅱ卷第12題)(多選題)對任意x,y,x2+y2-xy=1,則

( )

A.x+y≤1 B.x+y≥-2

C.x2+y2≤2 D.x2+y2≥1

【答案】BC

所以x2+y2≤2,當且僅當x=y=±1時等號成立,故C對.

由已知得x2+y2-xy=(x+y)2-3xy=1,

所以-2≤x+y≤2,故B對.

法二:令x+y=t,則y=t-x,

換元

代入x2+y2-xy=1,

可得x2+(t-x)2-x(t-x)=1,

聯立

整理得3x2-3tx+t2-1=0.

因為該方程有根,

所以Δ=9t2-4×3×(t2-1)≥0,

列式

解得-2≤t≤2,即-2≤x+y≤2.

求解

令x2+y2=t(t>0),則t-xy=1,

換元

整理得y4-ty2+(t-1)2=0,

聯立

因為該方程有根,

列式

求解

【方法點評】由已知條件x2+y2-xy=1及問題的結構特征,該題首先容易想到的是法一,即利用基本不等式及其變形求解.法二是利用換元法構造一元二次方程,然后再用判別式建立不等式去x+y,x2+y2的范圍.對比法一、法二可知,法一的計算量、思維量要比法二要小,是解決本題的最優解法.所以在平時的教學中,對于典型的習題要注意歸納總結各種不同的解法,并熟練掌握處理此類問題的通性通法,但在掌握基本方法的同時,要學會分析、比較,在會做的基礎之上尋找解決問題的最優解法,唯有如此,當學生遇到不同問題時,才會選擇恰當的方法,解題時少走彎路.

( )

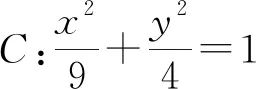
A.13 B.12 C.9 D.6

【答案】C

【詳解】法一:由橢圓的定義知

|MF1|+|MF2|=2a=6,

所以|MF1||MF2|≤9,當且僅當|MF1|=|MF2|=3時等號成立,

則|MF1|·|MF2|的最大值為9.

法二:設|MF1|·|MF2|=t(t>0),

換元

由已知得a2=9,b2=4,

則|MF1|+|MF2|=2a=6 ①,

|MF2|2-6|MF2|+t=0,

聯立

因為該方程有正根,

又t>0,所以Δ=62-4×t≥0,

列式

解得t≤9,則|MF1|·|MF2|的最大值為9.

求解

【真題4】(2020年高考數學課標Ⅱ卷理科)△ABC中,sin2A-sin2B-sin2C=sinBsinC.

(1)求A;(2)若BC=3,求△ABC周長的最大值.

【解析】(1)由正弦定理可得

BC2-AC2-AB2=AC·AB,

(2)法一:由(1)及余弦定理知AC2+AB2+AC·AB=9,即(AC+AB)2-AC·AB=9,

由基本不等式得

即4(AC+AB)2-36≤(AB+AC)2,

整理得(AC+AB)2≤12,

又AC+AB>3,

法二:令AC+AB=t(t>0),

則AC=t-AB,

換元

由(1)及余弦定理得BC2=AC2+AB2-2AC·ABcosA=AC2+AB2+AC·AB=9,

即(AC+AB)2-AC·AB=9 ①.

把AC=t-AB代入①式整理得

AB2-t·AB+t2-9=0,

聯立

列式

求解

【解析】法一:因為x>0,y>0,x+2y=5,

換元

因為該方程有正根,

構造

列式

求解

【真題6】[2018年高考數學課標Ⅲ卷(理)6題]直線x+y+2=0分別與x軸、y軸交于A,B兩點,點P在圓(x-2)2+y2=2上,則△ABP面積的取值范圍是

( )

A.[2,6] B.[4,8]

【答案】A

整理得|x-2+y|≤2,∴0≤x+y≤4,

則2≤x+y+2≤6,

∴S△PAB∈[2,6].

令t=x+y+2 ①,

換元

則①代入圓的方程整理得

2x2-2tx+t2-4t+6=0,

聯立

根據題意該方程有解,則有

Δ=4t2-4×2×(t2-4t+6)≥0,

列式

解得2≤t≤6,

求解

∴S△PAB∈[2,6].

【試題點評】

1.從時間和形式上來說,以上六道真題,從2018年到2023年,時間跨度為六年,形式上從老高考到新高考,試題的呈現形式年年不同,但考查的數學思想是不變的,用的是一種數學方法,即不等式方法,這充分體現了高考試題標新不立異,立異不偏離,常考常新,年年創新的特點.

2.從命題情境角度來說,以上六道真題是毫不相干的題目,分別考查了二元二次方程、橢圓、解三角形、直線與圓等相關的知識.但是從方法二的角度來說,相同的都是一種解題模式,即換元、聯立、列式、求解.充分體現了高考試題對于同一考點可以變換角度與變換題型再考,也就是說同樣的情境,今年這樣問,明年那樣問.

3.從方法的優越性來說,上述解析中的法一與法二孰優孰劣是相對于問題而言的,比如對于【2023年高考全國乙卷數學(文)第11題】來說,利用換元法構造不等式就比使用基本不等式簡便,但對于【2021·新高考Ⅰ卷第5題】來說,利用基本不等式就比換元法構造不等式簡便.因此平時的教學中,在會做的基礎之上,指導學生去尋找最優的解題方法,因為高考是選拔性考試,只有保證每道試題用的都是最優的解題方法,才能縮短解題時間,才有可能取得優異成績.

四、教學啟示

以上六道年份不一樣、情境不一樣的高考真題,解題方法最終歸根到底都回歸到課本上的2019年人教A版必修第一冊58頁第5題,真正做到了萬變不離其宗,而以這種思想可以解決的多元范圍問題在歷屆高考中頻頻“出鏡”.具體如下表所示:

序號年份題型知識點題號難度12018年江蘇填空題解三角形16中偏難22017年北京文科填空題多元問題11中偏難32016年山東解答題解三角形17中檔42015年湖南解答題解三角形17中檔52013新課標Ⅱ卷理科解答題解三角形17中檔62014年重慶選擇題多元問題6中檔72014高考數學課標Ⅰ理科填空題解三角形16中偏難82012年浙江選擇題多元問題9中檔92011年浙江填空題多元問題16中偏難

事實勝于雄辯,一道道高考真題告訴我們,高考試卷題目是立足于課本,根據課本上的題目加以擴展而來的.教材中的例題、習題是基礎,是根本,是非常重要的.因此在高考數學的備考中,教師和學生都要過課本上的例題關、習題關.教材中的每一道例題、習題都要研究透徹,掌握它的通性通法,掌握它的知識內涵.研究教材,深入挖掘可以作為知識考查載體的題目,深入探討有拔高潛力的題目,充分發揮例習題的隱藏功能,這樣在高中數學的教學中、在高考的備考中少走彎路,能夠起到事半功倍的效果.

綜上所述,在數學教學中,通性通法的使用和深層次的理解伴隨一個螺旋上升、逐步深化、直達本質的過程.只有真正重視通性通法,多方位、多側面地深入理解和系統總結,才能讓學生抓住數學問題的本質,將學生的知識學習引向深入的探究,提升學生的數學學科核心素養.