重通法育素養 溯源頭探本質
——以2023年高考數學全國甲卷理科第20題的解法探究為例

肖皓月 官聖淇 張 君

(四川省溫江中學)

2023年高考數學全國甲卷緊扣黨的二十大報告精神,反映新時代基礎教育課程理念.試題總體設計角度新穎,注重數學本質,突出理性思維,強調數學與生活及其他學科的聯系,滲透數學文化,積極引導中學數學教學注重對數學學科素養的培養,發揮高考“指揮棒”作用.高考是高中課堂教學的風向標,本文以2023年高考數學全國甲卷理科第20題為例,從通性通法到秒殺解法,從不同的切入點探討該題的解答,為解決此類解析幾何試題提供參考.

2023年高考數學全國甲卷理科第20題,是一道以解析幾何拋物線為背景設置的函數(最值)問題,形式新穎,綜合性強,對考生的能力要求較高,特別是對高水平的考生區分較好.圓錐曲線中的最值(或取值范圍)問題一直是歷年高考數學試卷中的熱點題型之一,常考常新,不斷創新,形式各樣,多以壓軸題形式出現.此類問題對考生的代數恒等變形能力、數學運算能力、推理論證能力等都有較高的要求,同時突出對數學知識、數學思想方法、數學核心素養的考查,具有較好的選拔性與區分度,備受命題者青睞.

1 真題呈現

(1)求p的值;

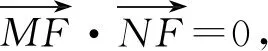
2 真題剖析

2.1 第(1)問解法探究

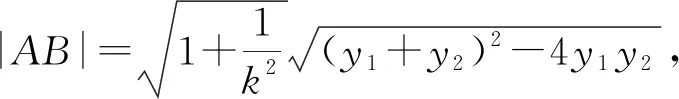
第(1)問思維導圖如下:

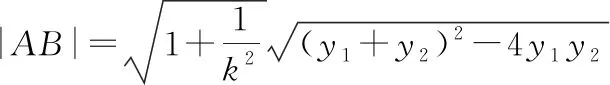
2.2 第(2)問解法探究

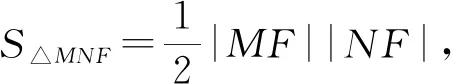
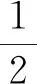
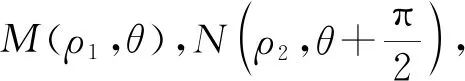
第(2)問思維導圖如下:

3 解法探究

3.1 第(1)問解答

設A(x1,y1),B(x2,y2),

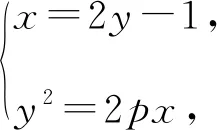
則y1+y2=4p,y1y2=2p,

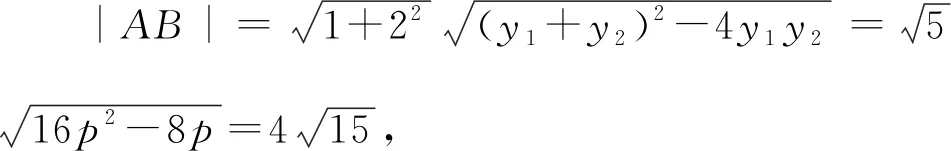
所以2p2-p-6=0.

又p>0,解得p=2.

3.2 第(2)問解答

3.2.1 思路一:綜合條件,線參法化為二次函數最值

解法1：設M(x3,y3),N(x4,y4),

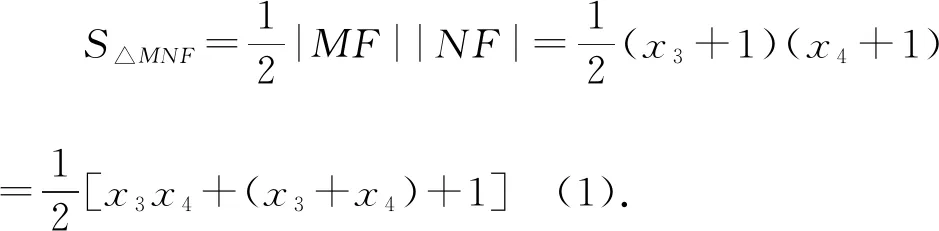
當直線MN斜率不存在的時候,設直線MN:x=s,則M(s,y3),N(s,y4),

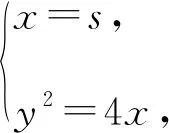
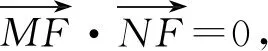
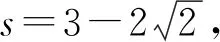
當直線MN斜率存在的時候,設直線MN:y=kx+t,

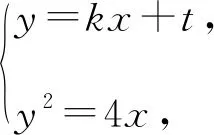
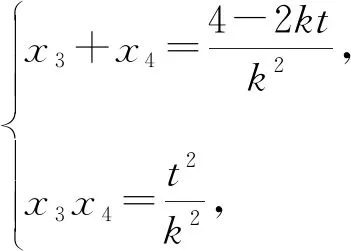
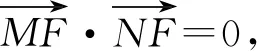
則(x3-1)(x4-1)+(kx3+t)(kx4+t)=0,

所以(x3-1)(x4-1)+(kx3+t)(kx4+t)=0,

所以(1+k2)x3x4+(kt-1)(x3+x4)+t2+1=0,

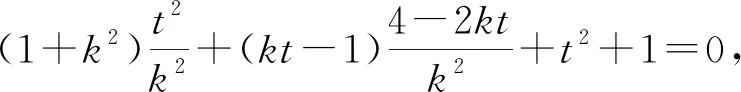
即t2+6kt+k2=4,

又t2+6kt+k2=4,

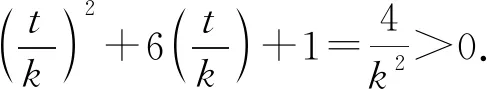
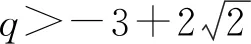
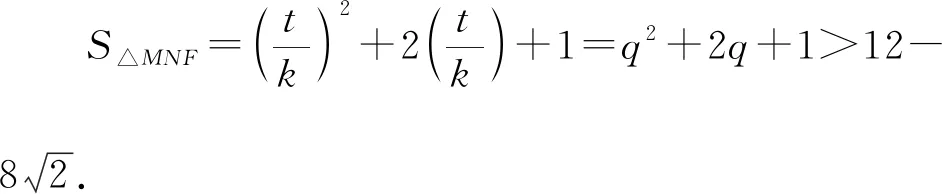
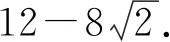
解法2：設M(x3,y3),N(x4,y4),易知直線MN斜率必不為0,則設直線MN:x=my+n,

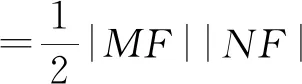
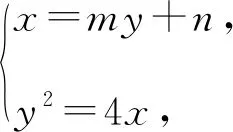
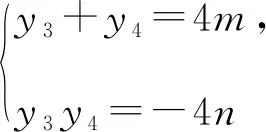
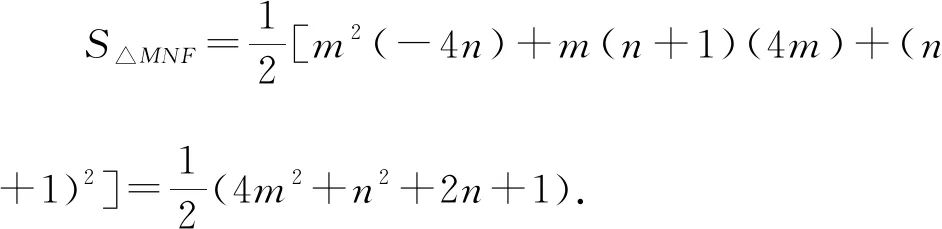
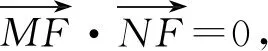
則(x3-1)(x4-1)+y3y4=0,

所以(my3+n-1)(my4+n-1)+y3y4=0,

所以(m2+1)y3y4+m(n-1)(y3+y4)+(n-1)2=0,

所以(m2+1)(-4n)+m(n-1)(4m)+(n-1)2=0,

所以4m2=n2-6n+1,

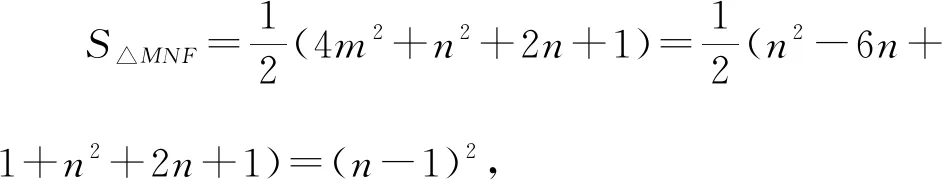
又4m2=n2-6n+1≥0,

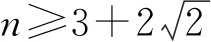
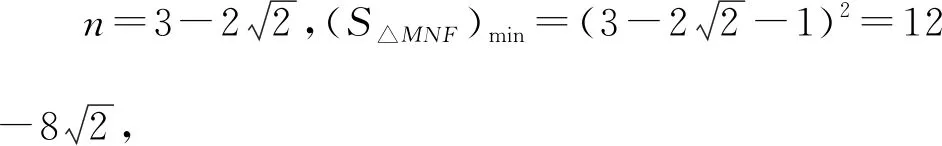
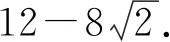
解法3：設M(x3,y3),N(x4,y4),易知直線MN斜率必不為0,則設直線MN:x=my+n,

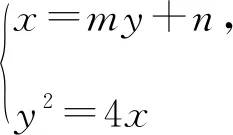
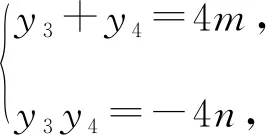
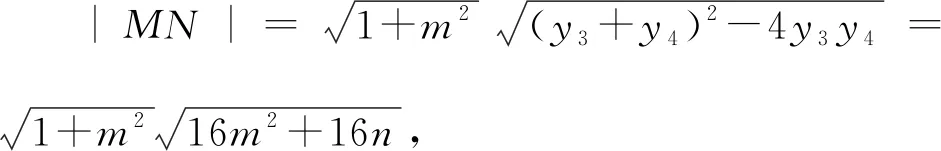
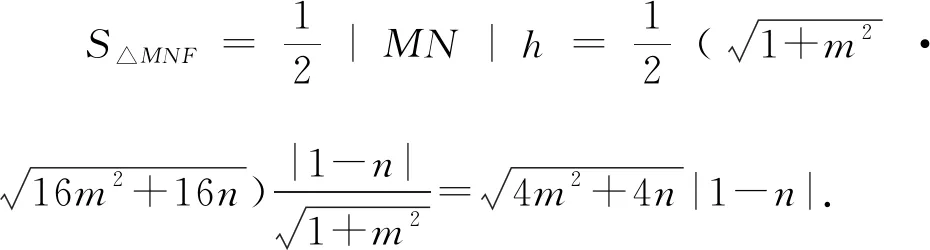
又有解法2知4m2=n2-6n+1,

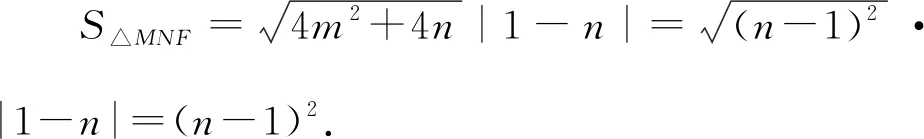
以下同解法2.

解法4：設M(x3,y3),N(x4,y4),易知直線MN斜率必不為0,則設直線MN:x=my+n,則設直線MN與x軸交于Q(n,0).

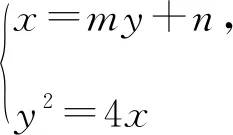
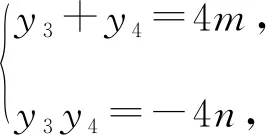
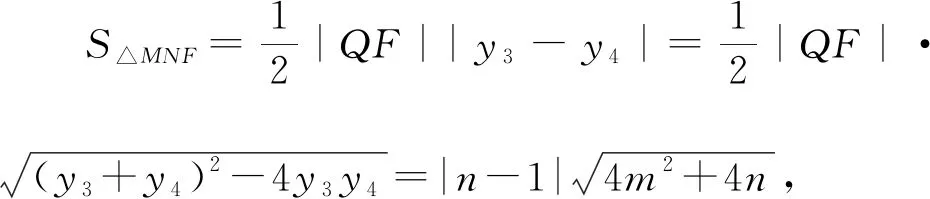
以下同解法3.

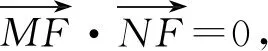
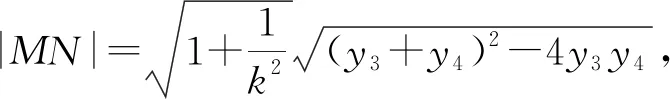
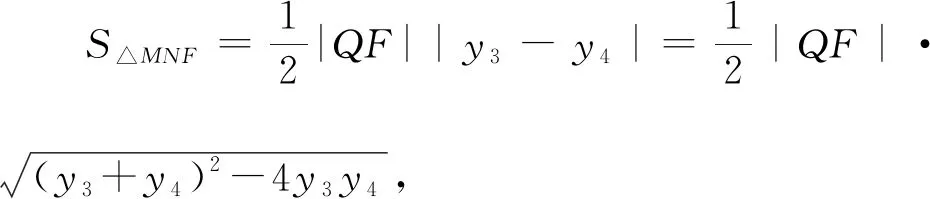
思路一主要思想是設直線方程,最終轉化為二次函數最值問題.

3.2.2 思路二:點參法轉化函數最值問題

解法5：設M(x3,y3),N(x4,y4),

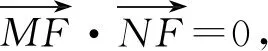
則(x3-1)(x4-1)+y3y4=0,

則x3x4-(x3+x4)+1+y3y4=0.

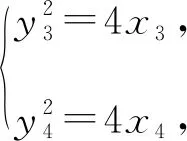
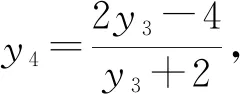
則由三角形面積的坐標式可得:

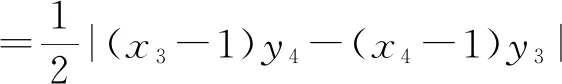
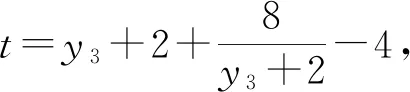
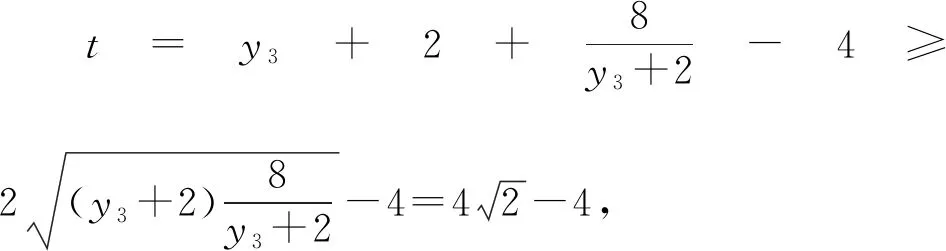
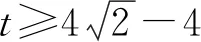
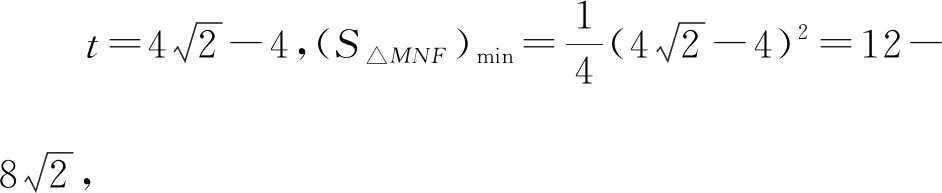
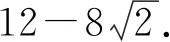
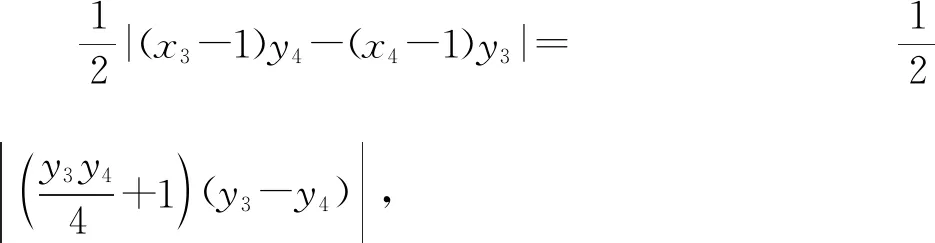
3.2.3 思路三:合理運用條件,引入角度參數

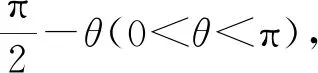
由拋物線定義,|MF|=|MF|cosθ+2,

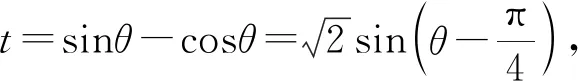
又t2=(sinθ-cosθ)2=1-2sinθcosθ,

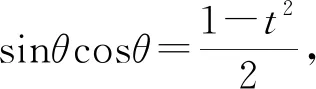
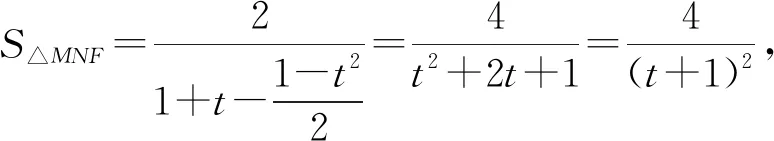
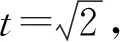
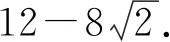
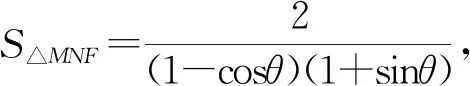
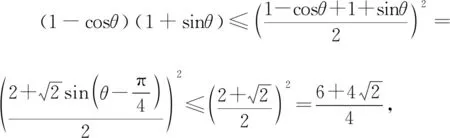
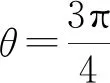
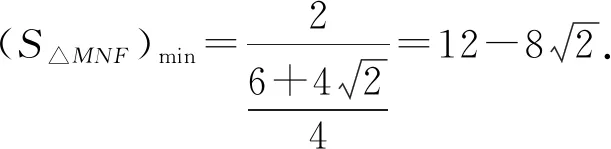
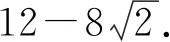
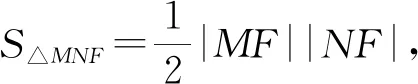
3.2.4 思路四:極坐標法簡化運算

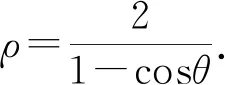
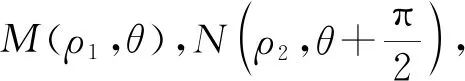
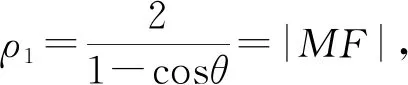
又t2=(sinθ-cosθ)2=1-2sinθcosθ,

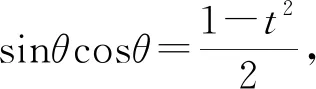
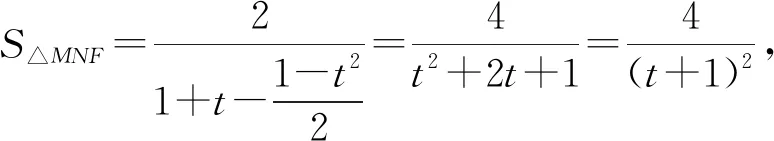
以下同解法6.

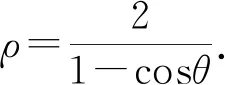
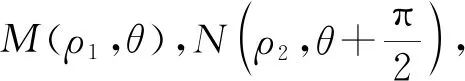
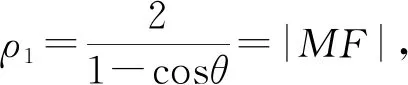
要求S△MNF的最小值,即求(1-cosθ)(1+sinθ)的最大值.

以下同解法7.

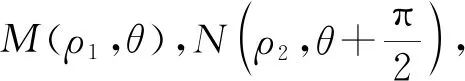
4 追本溯源

圓錐曲線中面積最值問題是高考中的熱點和難點問題,此類問題常與函數、三角、不等式等知識有機結合綜合考查.此題解法一方面注意選取合適的面積公式,從而求得面積表達式.另一方面要合理使用條件將面積表達式轉化為函數問題,我們可以追溯到2015浙江高考19題,讀者可仿照上文中解法給出第(2)問對應的解法.

(1)求實數m的取值范圍;

(2)求△AOB的面積最大值(O為坐標原點).

5 題后反思

這道高考題,考察拋物線中三角形面積最值問題,以拋物線為載體,將拋物線、三角形、函數等多項內容結合起來考察知識、思想方法、能力綜合功能,對學生數學素養要求較高.知識方面:考察直線方程、韋達定理,弦長公式、點到直線距離、三角形面積公式、拋物線定義與性質、基本初等函數(二次函數、基本初等函數、三角函數等)性質,基本不等式等多項知識;思想方法方面:考察到函數與方程、數形結合、化歸與轉化、分類討論數學思想;能力方面:考察數學運算能力、直觀想象能力、邏輯推理能力、數據處理能力.

圓錐曲線面積最值問題本質其實就是函數最值問題,解決此類問題常分兩步:第一步:選擇合適的面積公式.可用公式法或割補法或者坐標法求取三角形面積.第二步:轉化為函數最值問題.這一步也尤為重要,一方面我們可以選擇線參法或者點參法,將面積轉化為雙元問題,然后根據題設條件,尋求雙元之間關系,轉化為單元問題,最終轉化為函數最值問題.另一方面,在一些情況下若涉及焦半徑等,可以選擇角度為參數或者極坐標法,直接將面積轉化為單元問題,極大減輕計算量.

數學教學中,解決此類問題,教師應把握問題本質,落實素養導向.應引導學生多角度多方法進行探索,感悟其中的變與不變,總結多種解題方法,感悟其中數學思想.重視通法,培養數學素養,追根溯源,探索問題本質!