例談2023年高考數學試題中的數學文化及教學的實施建議

劉 洋

(吉林省教育學院)

隨著高中新一輪的課程改革,重視數學文化,在日常教學和高三備考中滲透數學文化,已成為必然趨勢.

在2017年版2020年修訂的《課程標準》第三章課程結構中說明了數學文化是指數學的思想、精神、語言、方法、觀點,以及它們的形成和發展;還包括數學在人類生活、科學技術、社會發展中的貢獻和意義,以及與數學相關的人文活動.并多次強調將數學文化融入課程內容,由此可見,數學文化的滲透十分重要.作為高中數學教師,要在學生的基礎知識和基本技能上下功夫,還要注重挖掘學生的探索精神和創造精神,使他們感知數學的文化內涵,并將其轉化為自己的數學文化氣質,具有簡化分析和解決問題的意識和能力,喚醒學生對數學文化的覺醒.對于高三年級更應關注數學文化類試題的研究和基于此的數學課堂的數學文化滲透和拓展,以便于更好地培養學生的核心素養,助力高考.

一、數學史及相關試題對數學課堂文化結構的改造

在教學中,在平時跟學生的溝通中,我們可以以教材、校本課程和課外閱讀作為載體,通過舉辦相應的數學文化講座、座談甚至是辯論賽等主題活動,讓學生閱讀更多關于數學史書籍,使其求知欲和數學素養得到充分的滿足,提升和施展,用正確的方式來發現數學的本質.數學史是很好的教學工具,可以讓學生通過故事認識所學知識的前世今生,從而避免一些因為認知障礙而產生的問題.

高三學習任務繁重,數學題的難度會整體上升,對于學生來說比較吃力,容易產生挫敗情緒,學生的沮喪情緒會使他們有些懷疑自己在數學方面的學習理解能力,影響備考.此時教師可以通過滲透數學文化元素的方式來調節學生的情緒和增強學生的信心.

例如,在學習三角函數時,2019年人教A版必修第一冊中的“三角與天文學”,就是一個非常好的切入點,學生自主閱讀,教師從側面加以輔助,可以使學生更好地認識三角函數,消除對于三角函數的恐懼心理.學習欲望呼之欲出.又如:

(1)求C的方程;

(2)記C的左、右頂點分別為A1,A2,過點B(-4,0)的直線與C的左支交于M,N兩點,M在第二象限,直線MA1與NA2交于點P,證明:點P在定直線上.

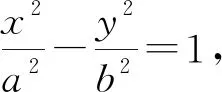
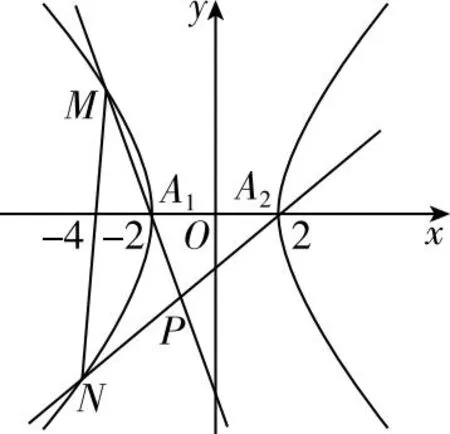
【分析】本題考查對雙曲線標準方程的理解與掌握,直線與雙曲線的位置關系,體現高考評價體系四層中的必備知識和關鍵能力.第(2)問考查直線與雙曲線的位置關系,可以從多個角度理解直線MN.本解法是把M,N看成直線MN與雙曲線的兩個交點.試題考查考生面對不確定性數學問題時,分析問題和解決問題的能力.試題背景中的兩個主要幾何元素——直線和雙曲線中,雙曲線是確定的,而直線MN是變化的,學生在分析問題時要注意.首先,對于變化的直線,要進一步分析引起MN變化的參變量是哪一個,或者是由哪個方式帶來的變化.其次,學生要認識到無論是什么方式帶來的直線MN的變化,都需要處理直線與雙曲線引出的一元二次方程的根與系數的關系.

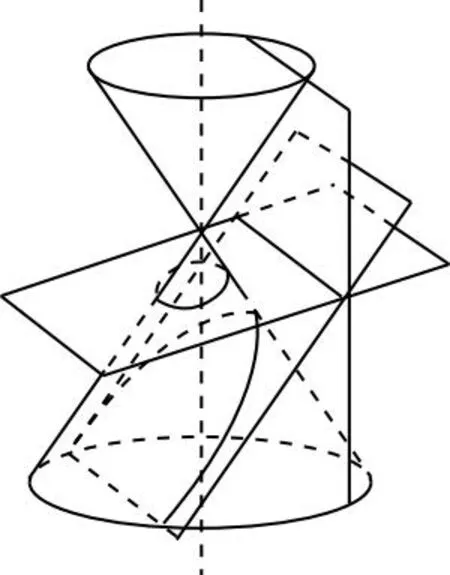
教師在講解過程中可以引申到圓錐曲線的發展歷史,緩解枯燥的課堂氛圍.圓錐曲線經歷了三個主要歷史發展階段:古典幾何階段的圓錐曲線理論:綜合古典幾何,研究幾何性質;坐標幾何階段的二次曲線理論:綜合利用代數方程與古典幾何的理論,研究圓錐曲線的代數結構;射影幾何階段的圓錐曲線理論:通過變換幾何中的射影變換(含仿射變換),研究射影不變量.不同的歷史發展階段對圓錐曲線的研究內容、研究方法和研究重點相互聯系又有明顯區別.本題在考查形式上綜合了圓錐曲線的幾何性質及射影不變量理論,在方法上綜合了代數與幾何的理論,具有深刻的數學意義及背景.

作為高考數學考查的重點,圓錐曲線具有悠久的發展歷史,在天體物理領域有著舉足輕重的地位.古希臘數學家阿波羅尼斯采用平面切割圓錐的方法來研究這幾條曲線.阿波羅尼斯曾為橢圓命名為“虧曲線”,為雙曲線命名為“超曲線”,為拋物線命名為“齊曲線”.值得一提的是,阿波羅尼斯得到了現在在高中數學中所有關于圓錐曲線的性質和結果,而他只是運用純幾何方法就做到了.16世紀時,德國天文學家開普勒在哥白尼的日心說的基礎上繼續研究,發現了行星是按照橢圓軌道,環繞太陽運行的這一現象;意大利物理學家伽利略也發現了物體斜拋運動的軌跡就是拋物線.這兩個發現給人們提供了靈感.通過以上事實對圓錐曲線的現實意義進行研究和完善,數學家們發現,圓錐曲線不僅是存在于圓錐面上的一類靜態曲線,它還在現實世界中,是物體運動的普遍形式.在1579年,蒙蒂基于天文學的研究帶來的啟發,修改橢圓的定義為:到兩個焦點距離之和為定長的動點的軌跡.我們高中階段橢圓的方程式也是根據這個定義推導出來的.

高三數學教師在有關圓錐曲線的教學中可以抓住其發展歷史脈絡,滲透學科本質,透過數學試題發現數學問題,進一步促進學生數學素養的提升.

二、通過展現數學的美,滲透數學文化和素養

有些時候,數學的美可以讓學生獲得解決數學問題的思路和方向.我們在面對實際問題需要理清其內在聯系時,可以運用數學的直觀審美,將數學問題的條件,特征與數學問題的結論聯系起來.教師可以根據學生認知發展水平,設計各種方式的活動、問題,逐步提升學生的數學審美水平和興趣,使學生在需要運用數學知識解決問題的時候,可以迅速正確地選擇思考方向,確定解決問題的具體方法.如:

【例2】(2023年高考數學新課標Ⅰ卷第12題)下列物體中,能被整體放入棱長為1(單位:m)的正方體容器(容器壁厚度忽略不計)內的有

( )

A.直徑為0.99 m的球體

B.所有棱長均為1.4 m的四面體

C.底面直徑為0.01 m,高為1.8 m的圓柱體

D.底面直徑為1.2 m,高為0.01 m的圓柱體

【答案】ABD

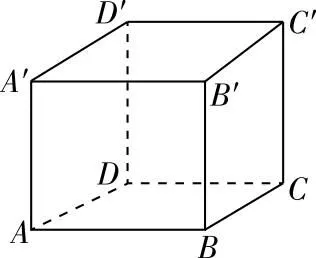
本題是一道生活類型的立體幾何題,考查學生的幾何美感與幾何直覺.首先,各正確選項中的物體均滿足一定的對稱性.例如選項D中的六邊形截面是考慮到了“正方體繞其體對角線旋轉120°后不變”這一對稱性,并且這個截面的最大性(面積最大,內部所含圓盤也最大)與該對稱性緊密相關,幾何直覺好的學生比較容易想到這個最優截面.選項B中正四面體的放置也關系到“四面體繞正方體的體對角線旋轉120°后不變”這一對稱性.有對稱性視角的學生比較容易想到幾何體的放置方法,試題考查學生靈活運用學科知識解決實際問題的能力,有利于選拔數學素養較好的考生,選拔創新型人才.

數學的美體現在教材、試題的每一個角落,不僅體現在知識的例子上,也體現在每節課后的閱讀和思考上.教師要注意提煉和整合教材中蘊含的數學美,引導學生逐步學會觀察、欣賞數學美,提升數學美的素養和做題直覺,在生活中都能用數學的眼光觀察世界,在做題時能夠有基于美感的直覺,指導他們順利解題.激發學生的學習興趣和學習動力,讓想象的翅膀在精彩的數學課堂豐滿起來,讓學生思維的智慧火花燃成灼熱的太陽,充滿力量,無畏困難.

三、通過數學思維方法的訓練體現數學文化

目前數學教育主要可以分為兩個方面,一是對于數學知識的傳授,二是對于數學的思想方法、能力、核心素養的提高.

在高中時期,轉化劃歸,數形結合,函數與方程,分類討論,特殊與一般等是最常用、最主要的數學思想方法.作為一線數學教師,在講解試題時,重點是提取其中所涉及的思想.培養學生在遇到問題難以直接解決時,通過適當的轉化,將原有的問題轉化為更熟悉、更容易的問題,從而解決原有問題的能力.從會解決一個問題到可以解決一類問題,達到舉一反三,一舉多得的效果.這就是改造思想,培養素養.舉例來說:

1.數形結合的思想

( )

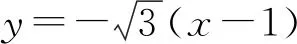
A.p=2

C.以MN為直徑的圓與l相切

D.△OMN為等腰三角形

【答案】AC

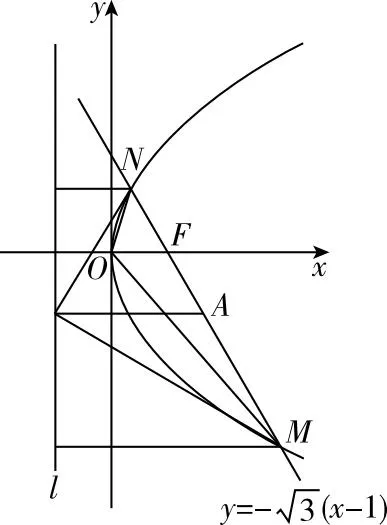
教師在教學中,讓學生具備識別和運用數形結合思想的數學思維,從而實現解題思想的升華和方法論的提升,觸類旁通.

2.轉化化歸的思想

【例4】(2023年高考數學新課標Ⅱ卷第6題)已知函數f(x)=aex-lnx在區間(1,2)上單調遞增,則a的最小值為

( )

A.e2B.e C.e-1D.e-2

【答案】C

本題是常規題型,在教材上也有類似題型.考查函數單調性與導數的關系,考查不等式的綜合運用.同時考查學生靈活運用導數相關知識,分析函數性質的能力,考查學生變未知為已知的化歸與轉化的能力.函數在(1,2)上單調遞增轉化為導數在該區間非負恒成立問題,通過分離參數轉化為不等式恒成立問題.通過構造新函數求其在(1,2)的值域進而得到a的最小值.

轉化與化歸思想在解題中經常運用,主要有直接轉化、等價轉化、正與反的相互轉化、一般與特殊的轉化等不同的轉化思路和方式.

因此,教師在講解此類問題時,要幫學生建立靈活的解題思維意識,多角度,全方位分析試題,運用不同的轉化方式簡化問題,解決問題,真正做到舉一反三.

四、通過數學知識文化背景的運用拓展數學試題內涵

我們都知道數學很抽象,但數學問題也是從具體的事物中提煉出來的.他們源于現實生活、生產,并在科學技術和現實生活中都有廣泛的應用,具有深刻的數學文化背景.我們要牢牢抓住《課程標準》,充分利用日常的教學設計等讓學生在熏陶中成為有深厚的數學素養和科學精神的新一代學生.

( )

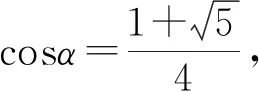
【答案】D

三角恒等變換學生非常熟悉,是高中數學課程的主干內容.學生理解三角函數的性質和運算之間的關系,就要從掌握三角恒等變換開始.從借助單位圓,直觀感受和理解三角函數的性質轉化,到通過代數運算理解并研究三角函數的性質.試題考查考生的運算求解能力.用到二倍角公式,其變形方式比較簡單.

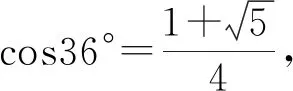
所以,在教學和復習中要關注數學知識在不同階段的縱向發展歷史脈絡,關注數學知識背后的文化意義,關注跨學科橫向聯系.在我們改編試題和命制試題時,試題背景的選擇和利用也需要我們認真考量.

五、基于數學文化的教學案例舉例

我們根據學生的認知規律,制定從特殊到一般,從具體到抽象的教學方法.多次結合數學史和數學文化,逐漸向學生滲透所講的數學知識.因為特殊就是直觀,就是具體也就是簡單,而抽象一般需要升華,需要歸納,需要總結,往往就需要很強的數學素養.

如,關于三角函數的概念,就經歷了由特殊到一般的過程,由直角三角形推出三角函數再到最后推出任意三角形的三角函數,正是遵循著這種規律.學生通過自我思考,合作探究和互相學習.能夠提升他們運用由特殊到一般的數學思想解決問題的能力,全面提升學生的數學素養.

在新課標的客觀背景下,在日常授課的同時,教師們也需要不斷學習,不斷提升,讓學生能夠在我們的課堂感受數學文化,學會思考,學會學習,全面提升數學素養.