凍融循環(huán)下FRP筋混凝土界面黏結(jié)強度預測

高 旭, 黃 麗 華

(大連理工大學 建設工程學院, 遼寧 大連 116024 )

0 引 言

纖維增強復合材料(fiber reinforced polymer,FRP)因其優(yōu)異的抗腐蝕性能,在惡劣環(huán)境下越來越多地應用在混凝土結(jié)構(gòu)中．

FRP筋混凝土的界面性能是控制結(jié)構(gòu)構(gòu)件完整性的主要因素[1]．凍融循環(huán)下FRP筋混凝土界面黏結(jié)機理復雜,已開展的大量試驗研究主要集中在定性分析上．羅小勇等[2]試驗研究發(fā)現(xiàn)凍融循環(huán)過程類似于疲勞損傷的反復積累,在荷載作用下GFRP筋肋破損嚴重,導致與混凝土的黏結(jié)性能退化．劉承斌等[3]通過試驗得出混凝土材料在凍融循環(huán)下劣化較為明顯．Yan等[4]試驗研究表明增加混凝土保護層厚度能提高凍融循環(huán)后的FRP筋混凝土界面黏結(jié)強度．金亮亮等[5]試驗研究發(fā)現(xiàn)隨著凍融循環(huán)次數(shù)的增加,FRP筋混凝土黏結(jié)性能不斷退化．杜從銘[6]通過拉拔試驗發(fā)現(xiàn)在凍融循環(huán)次數(shù)、混凝土基體強度以及BFRP筋直徑相同情況下,BFRP筋混凝土的峰值黏結(jié)應力隨著BFRP筋埋置深度的增大而減小．Khanfour等[7]試驗結(jié)果表明凍融循環(huán)對BFRP筋混凝土黏結(jié)強度影響較小．Alves等[8]研究了持續(xù)軸向荷載和凍融循環(huán)雙重因素下混凝土保護層厚度對GFRP筋混凝土黏結(jié)性能的影響．盡管凍融循環(huán)下FRP筋混凝土界面性能的試驗研究已大量開展,但是由于試驗條件不同以及影響界面性能因素較多,目前尚無通用的界面強度定量計算模型．

隨著計算機科學技術的發(fā)展,大數(shù)據(jù)、人工智能等數(shù)據(jù)分析和識別技術已越來越廣泛地用于解決工程問題．馬高等[9]基于CFRP約束混凝土圓柱試驗數(shù)據(jù),采用反向傳播神經(jīng)網(wǎng)絡(BPNN)構(gòu)建了便于應用的公式．陳健等[10]基于FRP筋混凝土拉拔試驗數(shù)據(jù),利用人工神經(jīng)網(wǎng)絡預測了FRP筋混凝土界面黏結(jié)強度．張芮椋等[11]從文獻中篩選條件參數(shù)各不相同的145組直拉試驗數(shù)據(jù),使用基因表達式編程建立了NSM FRP-混凝土黏結(jié)強度預測模型．鄧楚兵等[12]收集了不同類型FRP約束普通混凝土圓柱體的軸壓破壞試驗數(shù)據(jù),利用基因表達式編程建立了極限軸向應變與輸入?yún)?shù)之間的函數(shù)表達式．

本文利用遺傳算法優(yōu)化的反向傳播神經(jīng)網(wǎng)絡(genetic algorithm optimized back propagation neural network,GA-BPNN)以及基因表達式編程(gene expression programming,GEP)方法,基于凍融循環(huán)下FRP筋混凝土拉拔試驗數(shù)據(jù)構(gòu)建界面黏結(jié)強度計算公式．從文獻[2-7,13-20]中整理凍融循環(huán)下FRP筋混凝土拉拔試驗數(shù)據(jù)110組,隨機選取100組數(shù)據(jù)構(gòu)成訓練集用于網(wǎng)絡訓練,10組數(shù)據(jù)用于網(wǎng)絡精度測試．采用GA-BPNN方法預測凍融循環(huán)下FRP筋混凝土界面黏結(jié)強度,通過影響參數(shù)的敏感性分析,確定界面黏結(jié)強度計算模型的主要影響參數(shù),進一步利用GEP方法建立黏結(jié)強度與影響參數(shù)之間的函數(shù)表達式,通過與試驗數(shù)據(jù)和文獻模型對比,驗證本文模型可行性．

1 GA-BPNN模型

反向傳播神經(jīng)網(wǎng)絡的運行原理如圖1所示,通過適應度函數(shù)來選擇最優(yōu)模型,利用優(yōu)化后的權(quán)值和閾值作為后續(xù)反向傳播神經(jīng)網(wǎng)絡的初始權(quán)值和閾值,進而提高預測模型的精度,其具體流程如圖2所示．

圖1 反向傳播神經(jīng)網(wǎng)絡的運行原理

圖2 GA-BPNN流程圖

本文考慮了凍融循環(huán)次數(shù)(N)、最低溫度、單次凍融時間、試件破壞形式、FRP筋直徑(d)、FRP筋類型、混凝土抗壓強度(fc)、錨固長度(la)、歸一化的混凝土保護層厚度(C/d)、FRP筋表面形式10個界面性能影響參數(shù)作為神經(jīng)網(wǎng)絡的輸入層．其中FRP筋類型用數(shù)字1～3分別代表GFRP、BFRP、CFRP;FRP筋表面形式用數(shù)字1～5分別代表噴砂、纖維束螺旋纏繞且?guī)Ю摺Ю摺⒗w維束螺旋纏繞、噴砂且?guī)Ю?試件破壞形式用數(shù)字1～4分別代表拔出、FRP筋夾持處破裂、混凝土劈裂、FRP筋拉斷．具體變量的最小值、最大值、均值和標準差見表1．

表1 數(shù)據(jù)庫中變量的范圍

GA-BPNN訓練參數(shù)設置見表2,經(jīng)過試算本文采取的遺傳算法種群規(guī)模為100,最大迭代次數(shù)為1 000,交叉概率和變異概率根據(jù)經(jīng)驗以及訓練結(jié)果進行調(diào)整,分別取0.8和0.1．

圖3為GA-BPNN經(jīng)過多次迭代后網(wǎng)絡輸出與期望輸出的均方差,通過多次試算取GA-BPNN的迭代次數(shù)t為20 000,精度可達0.005左右．

采用訓練好的GA-BPNN模型,預測訓練集中100組數(shù)據(jù)和測試集中10組數(shù)據(jù),并與試驗結(jié)果對比,結(jié)果如圖4、5所示,回歸線斜率分別為1.003 5和0.999 2,決定系數(shù)R2分別為0.900 8和0.834 0．測試集中試驗值(τe)與預測值(τu)之比見表3,平均比值為1.047 1．

表2 訓練參數(shù)設置

圖3 訓練集輸出的均方差

圖4 預測值與試驗值對比(訓練集)

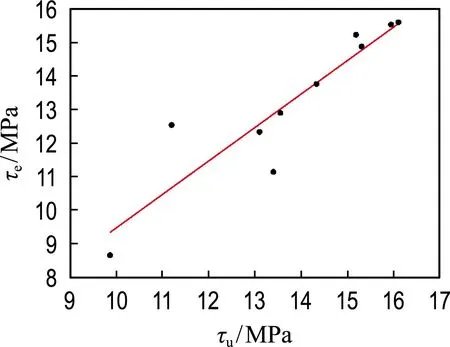
圖5 預測值與試驗值對比(測試集)

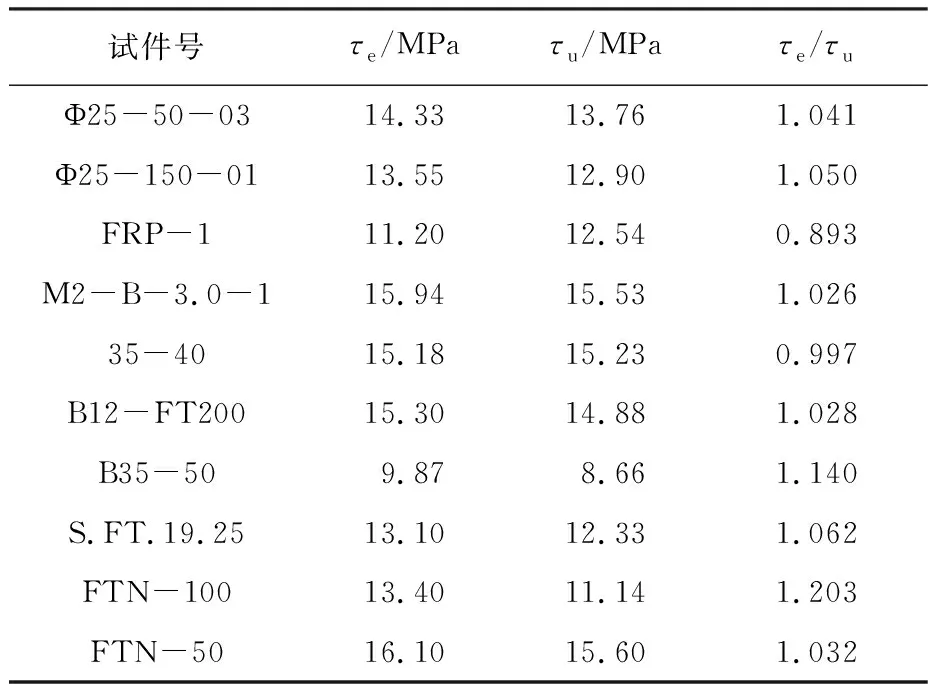
表3 測試集數(shù)據(jù)預測結(jié)果

2 輸入?yún)?shù)敏感性分析

目前基于神經(jīng)網(wǎng)絡的權(quán)重分析方法主要有Garson法[21]、Tchaban法(權(quán)積法)等．Garson法是一種利用神經(jīng)網(wǎng)絡各層之間連接權(quán)值進行權(quán)重分析的方法,基本原理是用連接權(quán)值的乘積來計算輸入變量對輸出變量的貢獻程度,Garson法相較于其他方法考慮了多個變量交互作用時對輸出的影響,計算公式如下：

(1)

式中：Rik為輸入層的第i個神經(jīng)元對輸出層的第k個神經(jīng)元的影響程度;Wij、Wjk分別為輸入層到隱含層、隱含層到輸出層的連接權(quán)值,i=1,2,…,n,k=1,2,…,m(n、m分別為輸入信號、輸出信號數(shù)量)．

本文將所選取的10個影響參數(shù)設為變量,即凍融循環(huán)次數(shù)(x1)、最低溫度(x2)、單次凍融時間(x3)、試件破壞形式(x4)、FRP筋直徑(x5)、FRP筋類型(x6)、混凝土抗壓強度(x7)、錨固長度(x8)、歸一化的混凝土保護層厚度(x9)、FRP筋表面形式(x10),將得到的神經(jīng)網(wǎng)絡模型采用Garson法進行參數(shù)敏感性分析,所得結(jié)果如圖6所示．

對比圖6中的10個輸入?yún)?shù)敏感性系數(shù)可以發(fā)現(xiàn),凍融循環(huán)次數(shù)(x1)、混凝土抗壓強度(x7)和歸一化的混凝土保護層厚度(x9)對界面黏結(jié)強度的影響占比最大,分別達到0.220、0.108和0.138,該結(jié)果與多數(shù)試驗研究的定性結(jié)論一致．

圖6 輸入?yún)?shù)的敏感性系數(shù)

3 基于GEP方法的界面黏結(jié)強度計算公式

GEP方法[22]是遺傳算法和遺傳編程的融合與升華．該方法在復雜函數(shù)發(fā)現(xiàn)和智能預測領域有著優(yōu)越的表現(xiàn),GEP方法操作流程如圖7所示．

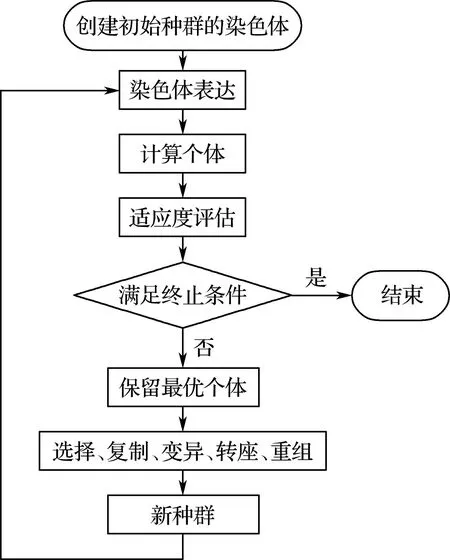
圖7 GEP方法操作流程

GEP方法包含基因語言和表達式樹語言,表現(xiàn)型編碼是按照基因型編碼的線性字符串,從左至右讀取字符,并將字符按相應的層次順序和語法規(guī)則進行排列,從而構(gòu)成GEP方法的表現(xiàn)型編碼,即表達式的樹結(jié)構(gòu)．若一個基因由集合{+,-,×,/,a,b,c,d}中的元素構(gòu)成,頭部基因長度為4,尾部基因長度為5,最大操作數(shù)為2,那么基因總長為9,則該基因編碼及對應的表達式樹如圖8所示．

圖8 基因編碼及對應的表達式樹

(2)

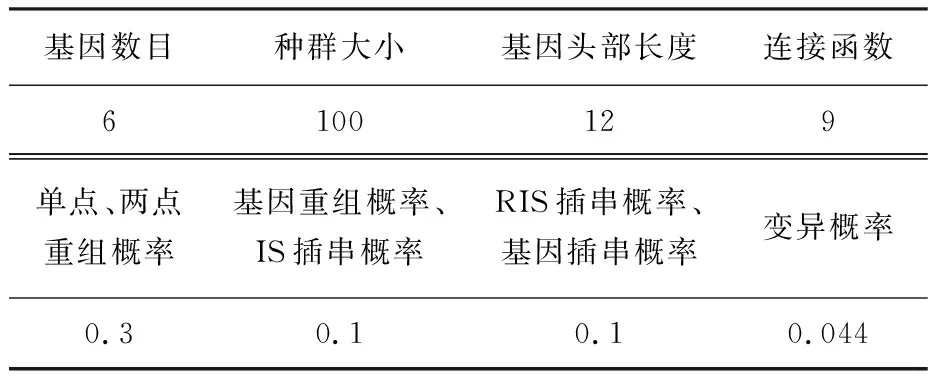
表4 GEP參數(shù)

按照表4設置的參數(shù)調(diào)試程序,可得到最優(yōu)染色體,其各基因的連接函數(shù)為“+”,得到的FRP筋混凝土界面黏結(jié)強度的預測模型函數(shù)表達如下：

(3)

由式(3)可見,混凝土抗壓強度、凍融循環(huán)次數(shù)、錨固長度出現(xiàn)頻次較高,對界面黏結(jié)強度計算結(jié)果影響較大．

4 GEP模型計算精度分析

利用式(3)計算的測試集中10組試驗數(shù)據(jù)結(jié)果(τu)見表5,與試驗結(jié)果(τe)對比的均方根誤差(RMSE)為1.024,平均絕對誤差(MAE)為0.877．100組訓練集數(shù)據(jù)預測結(jié)果的均方根誤差為4.089,平均絕對誤差為3.199．

表5 GEP模型的預測結(jié)果

目前國內(nèi)外文獻和規(guī)范中能夠查到的凍融循環(huán)下FRP筋混凝土界面黏結(jié)強度模型只有兩個．

(1)Deng等[13]2021年提出凍融循環(huán)下FRP筋混凝土界面黏結(jié)強度計算公式如下：

(4)

其中a0、a1、a2、a3、a4分別為-2.119 9、0.013 8、-14.599 4、0.002、-0.171,τu,c為凍融循環(huán)后界面黏結(jié)應力,N、d、la、C/d符號意義不變,ft(N)為相應凍融循環(huán)次數(shù)下的混凝土劈裂抗拉強度．

(2)羅小勇等[2]2014年提出了凍融循環(huán)下FRP筋混凝土界面黏結(jié)強度擬合曲線,計算公式如下：

τu=15.093 84-0.009 33N-1.723 12×10-5N2+1.584 48×10-7N3

(5)

將測試集中10組試驗數(shù)據(jù)代入式(4)、(5),分別計算模型的平均絕對誤差、均方根誤差、絕對誤差積分(IAE)及決定系數(shù)(R2)(表6)．與本文提出的GEP模型計算誤差對比可知,GEP模型的決定系數(shù)較高,平均絕對誤差、均方根誤差較小,絕對誤差積分在10%以內(nèi),表明GEP模型的預測精度更高,泛化性能更強．

表6 各模型預測結(jié)果的誤差統(tǒng)計

采用4種模型計算測試集中10組試驗數(shù)據(jù)得到的界面黏結(jié)強度如圖9所示,與試驗值對比可見,GEP模型以及GA-BPNN模型的計算結(jié)果更貼近試驗值,且變化趨勢與試驗值一致;文獻[13]模型在預測多次凍融循環(huán)下的界面黏結(jié)強度時結(jié)果偏差較大,原因在于其構(gòu)建模型的數(shù)據(jù)庫只包含0～50次凍融循環(huán)的試驗數(shù)據(jù);文獻[2]模型是一種取平均值的擬合方法,因此給出的界面黏結(jié)強度預測結(jié)果變化幅度小;GA-BPNN模型因其包含最多界面黏結(jié)強度影響參數(shù),故精度最高;GEP模型給出了凍融循環(huán)下界面黏結(jié)強度的具體計算公式,變量少,表達簡單,實用性更強．

圖9 各模型的預測值與試驗值對比

5 結(jié) 論

(1)基于大量試驗數(shù)據(jù),采用機器學習的方法預測FRP筋混凝土界面黏結(jié)強度,構(gòu)建的界面模型精度高且泛化性能強,其中GA-BPNN模型包含了影響界面黏結(jié)強度的10個參數(shù),預測結(jié)果精度最高;建立在主要影響參數(shù)基礎上的GEP模型,計算公式簡單,滿足精度要求,實用性更強．

(2)與目前文獻給出的界面黏結(jié)強度預測模型相比,本文建立在110組試驗數(shù)據(jù)基礎上的計算公式精度更高、包容性更強．

(3)基于神經(jīng)網(wǎng)絡的分析結(jié)果與多數(shù)文獻中的試驗結(jié)果一致,影響凍融循環(huán)下FRP筋混凝土界面黏結(jié)強度的主要參數(shù)包括凍融循環(huán)次數(shù)、混凝土抗壓強度、歸一化的混凝土保護層厚度、錨固長度及FRP筋直徑．