基于隨機化的混沌單分組散列函數的設計與實現

■尹滄濤，李永珍

（1.延邊職業技術學院，吉林 延吉 133000；2.延邊大學，吉林 延吉 133000）

隨著網絡技術和電子商務的迅速發展，保護數據的隱私和安全已經成為了一項極其重要的任務。為了更好地保護數據的安全，密碼學研究不斷向前推進，引入了許多新的技術和方法。其中，哈希函數就是密碼學領域中的一種重要技術。哈希函數是一種將任意長度的消息壓縮到固定長度的技術，它的輸出值稱為消息的哈希值或摘要。哈希函數是一種重要的不可逆加密算法，從而保護數據的完整性和安全性。本文對MD5 算法進行改進，意在進一步保護短消息在傳輸和保存方面的安全性。

一、相關理論基礎

（一）哈希函數及MD 系列

哈希函數是一種將任意長度的輸入數據映射為固定長度輸出的函數，哈希函數具有以下特性：唯一性、一致性、不可逆性、抗碰撞性。哈希函數在計算機科學和密碼學中有廣泛應用，例如，數字簽名、消息認證、密碼學中的密鑰派生等領域。常見的哈希函數包括MD 系列、SHA 系列、RIPEMD等。MD系列是由美國密碼學家Ronald Rivest 發明的一系列哈希函數，包括MD2、MD4、MD5 三種算法。這些算法都是基于Merkle-Damg rd 結構的迭代哈希函數，其核心思想是將消息分為若干個塊，對每個塊進行一系列的變換操作，最終得到一個固定長度的哈希值。

（二）混沌理論

混沌理論是一種研究非線性系統的數學理論，它最初被提出描述混沌現象，即一種看似隨機無序、但實際上有規律的現象。混沌理論由李天巖和Yorke J A 于1975 年提出[1]。現已成為一個廣泛研究的領域，涉及物理學、生物學、社會科學等多個領域，其具備下列特征：確定性、敏感性依賴、自相似性、穩定的隨機性、非線性。

混沌系統的輸出是非線性的、無規律的，并且受初始條件的微小變化而產生不同的結果，這些特性使得混沌系統的輸出可以被用作密碼學中的加密和解密。

目前混沌系統在密碼學中的應用主要體現在哈希函數的改造上。通過混沌系統的改造，可以使哈希函數的輸出更加隨機和無序，從而提高哈希函數的安全性和抗攻擊能力。

（三）隨機化結構

目前，對哈希函數的傳統攻擊手段，如長度擴展攻擊，第二原像攻擊，中間相遇攻擊等，都是以明確函數內部結構為前提。2004 年王小云教授等人提出了差分攻擊，成功地對具有MD 結構的算法進行了有效的碰撞，這進一步增加了哈希函數的安全隱患。差分攻擊是通過尋找哈希函數內部不同輸入值之間的差異，破解函數的攻擊方法。它利用哈希函數的差分特性，找出一些輸入的差異，從而推導出哈希函數的輸出差異。然后，通過這些輸出差異，可以生成兩個不同的輸入，使它們在哈希函數中產生相同的輸出，即碰撞攻擊。但當哈希函數的算法是不確定的時候，密碼分析將很難著手。對于一個固定的函數，要保證單向性是比較困難的，因為原則上可以根據哈希函數的結構進行逆推[2]。但是，在引入隨機函數的情況下，哈希函數的表達式、結構和形式可能是隨機的不確定的，因此，逆推哈希函數變得非常困難。

二、算法的設計與實現

（一）預處理階段

本設計所提出的哈希函數為更好的適應短消息加密，將輸入長度限制為1 bit 至128 bits。若不足128 bits，則填充1 個1 和多個0。將處理好的消息，分成A、B、C、D，4 組每組32 bits（見圖1）。

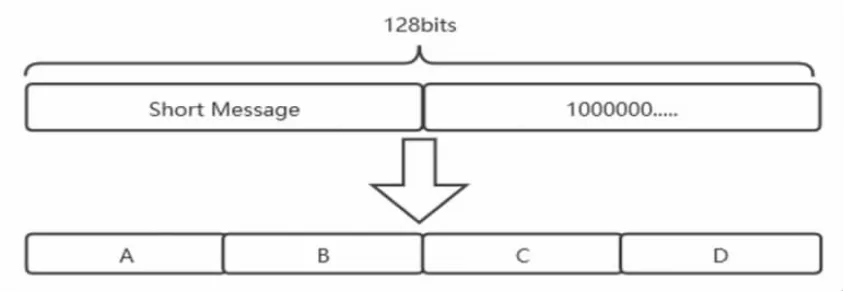
圖1 算法的初始化過程

對于安全的哈希函數，在已知哈希值和算法的時候，明文（消息）m 本質上是可以推導的，但是通過哈希值計算明文的困難讓我們通常地認為它是未知的，所以，如果哈希函數的具體形式由明文確定，即i=S(m)，哈希值H=fi(m)，則剛好滿足上面提到的“已知明文可以很容易確定函數的具體形式，已知哈希值很難確定函數的具體形式”的要求。為減少計算量，存儲量和復雜度，本設計在預處理階段確定哈希函數的具體形式。將預處理后的128 bits 內容，分為兩組M1 和M2，各64 bits。為消除預處理階段M2 填充1 和大量0 后可能產生的規律性。將M1 左循環移6 bits，M2 右循環移8 bits 后異或，并對1024 取模，結果為10 bits 的2 進制數。前8 bits 中，每2 bits 控制第2 節主循環中一個邏輯函數的具體形式。后2 bits 將被保存，并用于第3 節中混沌加密算法及其分形參數的確定。

（二）主循環邏輯

算法的主循環共經過4 輪，每輪4 步的邏輯運算，一共經過16 步運算，最終生成長度為128 bits 的輸出結果。將4 組待操作內容，分別與A，B，C，D 四個寄存器中的常量，按位與運算，在本步循環結束時獲得的運算變量替換循環前所保存的寄存器變量，用來更新寄存器內容[3]。圖2 描述了該算法主循環的整體邏輯。

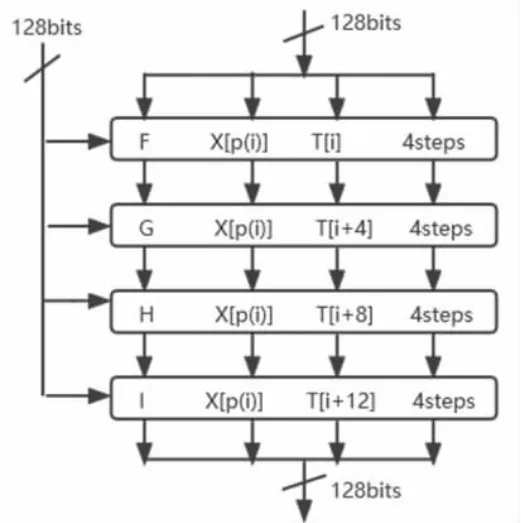
圖2 整體邏輯圖

其中，T 為128 bits 常數，其作用為對操作內容進行混淆，消除短消息內容上的規律性。F,G,H,I 為四個函數列表，內部各含有4 個不同的邏輯函數F=[f1,f2,f3,f4],G=[g1,g2,g3,g4],H=[h1,h2,h3,h4],I=[i1,i2,i3,i4]，每輪將選取列表中的一個函數參與4 步運算。

附表1 為隨機函數的定義，新設計的邏輯函數保證了結果滿足均勻分布的規律，從而確保循環后輸出結果具有統一分布。X[p（i）]為不同輪中分組的使用順序，p（i）函數具體形式如下：

附表1 隨機函數定義表

第一輪中：p（i）=i；

第二輪中：p(i)=(1+5i)mod 4；

第三輪中：p(i)=(5+3i)mod 4；

第四輪中：p(i)=7i mod 4；

（三）混沌加密算法

由于混沌映射具有良好的隨機性、初始值敏感性，與哈希函數設計原則極為貼切。因此，在過去幾十年中，有學者曾提出過具有混沌映射構建哈希函數的方案[4-6]，本設計將利用多種參數可變的混沌加密算法，對循環后的結果通過迭代處理的方式產生新的輸出值，以提高哈希函數的擴散性，整個混沌映射流程，見圖3。

圖3 混沌映射算法流程圖

由圖3 可知，為了將得到的A,B,C,D 四個寄存器的值轉換為16 個混沌映射的初始值，并落在(0,1)的值域上，首先需做如下線性變換：

βi為消息分塊后的ASCII 值。

定義可變參數的混沌映射算法如附表2 所示。

附表2 混沌映射定義表

這里將通過第2 節保存參數s，確定混沌映射的使用編號。本設計將μ 設為固定范圍的可變參數，為克服周期窗口對混沌映射的影響，其確定方式如下：

隨機參數μ 由線性同余隨機數發生器（LCG）產生，選取的混沌變換將進行36 次迭代。其中K1,K2,K3,K4 為上一輪輸出結果的分組，各32 bits。式（2）中233-1，根據文獻建議進行取值，其為一個較大的奇素數，產生的隨機數具有較大周期，保證了參數μ 的取值空間和隨機性。

經過36 輪迭代計算，得到的混沌序列為：

對迭代結果x36（1），x36（2），…，x36(16)通過公式進行逆變換。

其中floor（x）為向下取整操作，舍去小數點后的值，以提高哈希函數的單向性。根據式（4）可得到16 個0 至255 之間的整數，每個整數用8 bits 的2 進制數表示，最終將輸出128 bits 的結果。

三、實驗測試與分析

本節首先進行混沌的判別分析，驗證設計中的系統具備混沌狀態；再通過統計分析、雪崩效應以及算法效率三個方面，進行對比試驗，驗證設計的安全性以及效率。

（一）混沌的判別原則

混沌運動是非線性系統特定的運動形式，但是系統的非線性僅是出現混沌運動的必要條件而非充分條件[7]。其判別多先用數值實驗識別，再通過工程試驗驗證，實驗將采用以下兩種方式驗證系統具備混沌狀態，即李雅普諾夫指數法和分岔圖法。

證明一動力系統或自治微分方程穩定性的函數被稱為稱李雅普諾夫指數(Lyapunov Exponent)，簡稱LE。它沿某一個方向取值的大小與正負可用來描述動力學系統的相鄰軌道沿該方向的平均發散或收斂的快慢程度。正的李雅普諾夫指數越大，表示運行軌道越發散，使系統呈現出“既不收斂，也不發散，也不周期”的混沌態。一維李雅普諾夫指數計算公式如下：

其中λ 為李雅普諾夫指數，f(xi)為一維混沌映射函數。

分岔圖法中“分叉”指的是當系統中的控制參數略有變化時，如果整個動力系統的結構不穩定，系統的拓撲結構會突然改變。對于某個特定的參數，狀態變量在分叉圖上呈現為一個點或與系統等周期的點，這表明系統處于周期狀態；如果對于某個控制參數，分叉圖上有無數個點，并且每次狀態都不落在同一個點，則系統處于混沌狀態。

1.Logistic 映射

圖4 給出了Logistic 映射隨分形參數μ 變化的李雅普諾夫指數圖譜。從其圖譜可見，當參數μ∈[3.57,4]時，該映射的李雅普諾夫指數大于0，進入混沌狀態。圖5 給出了Logistic 映射的分岔圖，當參數μ 大于3.57 時映射取值范圍逐漸增大，符合混沌特點。

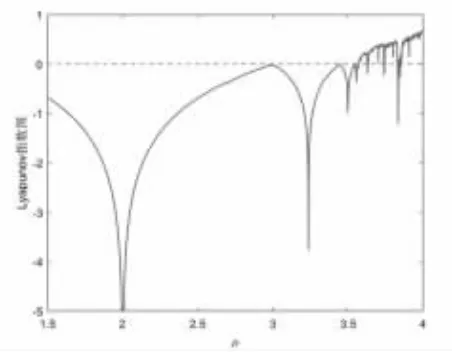
圖4 Logistic 映射李雅普諾夫指數圖譜

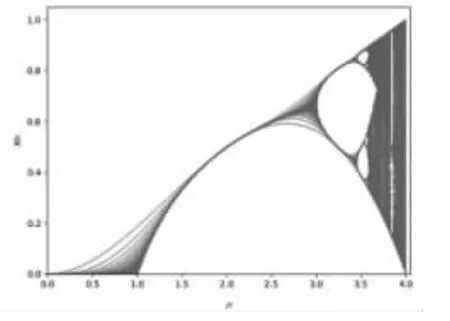
圖5 Logistic 映射的分岔圖

2.Tent 映射

Tent 映射常用于圖像加密系統，由圖6 可知，當參數μ 大于1 時，系統的李雅普諾夫指數皆大于0; 由分岔圖（見圖7）可知，當μ 大大于1.75 時，其取值范圍接近滿射。

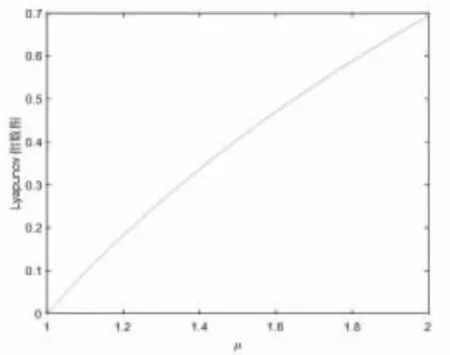
圖6 Tent 映射下μ 的李雅普諾夫指數圖譜

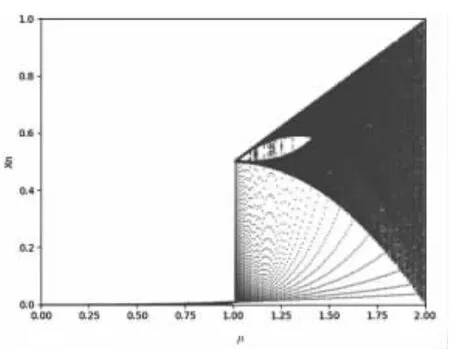
圖7 Tent 映射下分岔圖

3.Tent 映射

從圖8,9 中可見Chebyshev 映射的參數區間更大，李雅普諾夫指數也更大，說明其混沌性優于前兩者。當分形參數μ 大于1 時進入混沌狀態，大于2 時即可遍歷該區域所有狀態點。

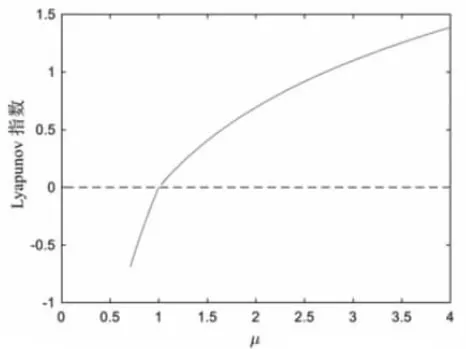
圖8 Chebyshev 映射李雅普諾夫指數圖譜

圖9 Chebyshev 映射分岔圖

4.Sine 映射

Sine 映射是混沌映射的典型代表，它的數學形式極為簡單，由圖10、圖11 可知當分形參數μ 大于0.87 時，其進入混沌狀態。

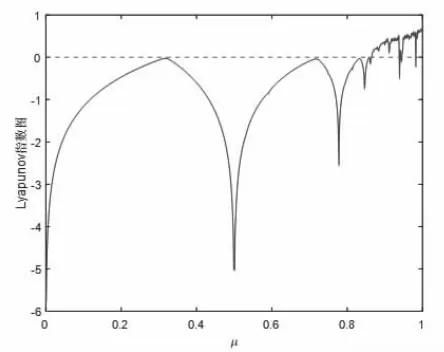
圖10 Sine 映射李雅普諾夫指數圖譜

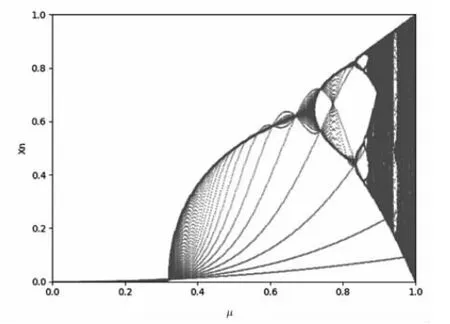
圖11 Sine 映射分岔圖

由上述實驗可知，本設計中可變參數μ 的取值范圍皆符合混沌要求，可通過迭代計算的方式，將消息通過處理得到的哈希值擴展到整個向量空間。

（二）統計分析

為確保哈希函數的安全性，要求其值域是均勻分布的，否則，攻擊者就能夠以低于暴力破解的代價找到哈希函數的碰撞[8]。本設計選取以下六個指標對哈希算法進行統計分析。

（1）最大變化比特數Bmax；

（2）最小變化比特數Bmin；

測試方法如下：首先選取1000 個長度介于1 bit 至128 bits 的短消息，計算輸出結果，再翻轉消息中任意1bit，計算改變后的輸出結果，將兩者對比得到結果，如附表3 所示。

附表3 統計分析結果

由統計測試結果可以看出，本設計提出的哈希函數平均變化比特數比傳統算法更接近于理想值，平均變化概率P 也非常接近于50%，平均變化比特數的均方差△B 和平均變化概率的均方差，P 均比傳統算法小，說明其變化幅度很小且非常穩定，同時Bmax和Bmin也較小。統計分析結果表明，本設計具有良好的抗統計攻擊能力。

（三）雪崩效應

哈希函數不同部件的數據關系越獨立，則越容易在密碼分析的過程中被逐個擊破。因此，良好的雪崩效應是一個優秀的哈希算法所應該具備的。實驗按照雪崩效應的原理來設計實驗，使用1000 對明文對，這些明文對每個都只有一位不同，通過比較兩個明文經過算法得到的結果中不相同的位數，來作為評判標準[9]。按照雪崩效應所描述的，其理想值應接近輸出結果位數的50%。

圖12—圖14 為本設計提出的算法與傳統算法的雪崩效應實驗結果，這里規定百分比大于60%的點和小于40%的點為壞點。經過統計發現各個算法壞點出現的概率如下。MD5：3.2%；單分組哈希函數SBH：2.25%；本設計提出算法：1.82%，從統計結果可以看出，添加具有隨機化參數的混沌映射使結果行成高度關聯、廣泛擴散的狀態，有效的提高了哈希函數的雪崩性和擴散效果。

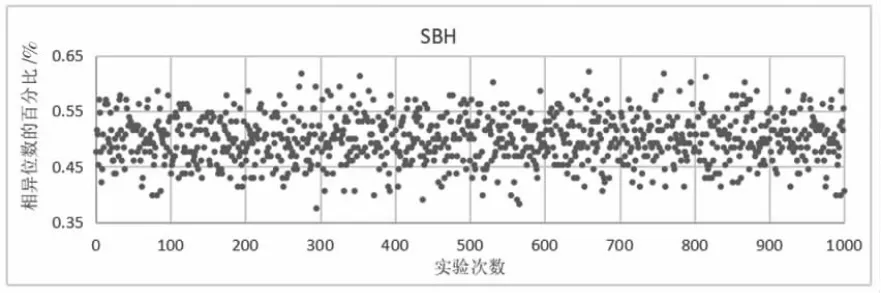
圖12 SBH 雪崩測試結果

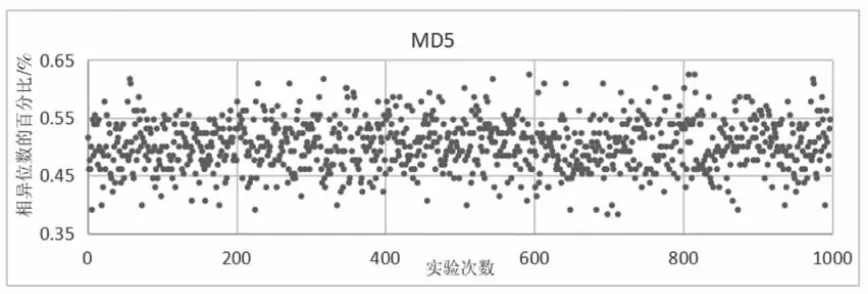
圖13 MD5 雪崩測試結果

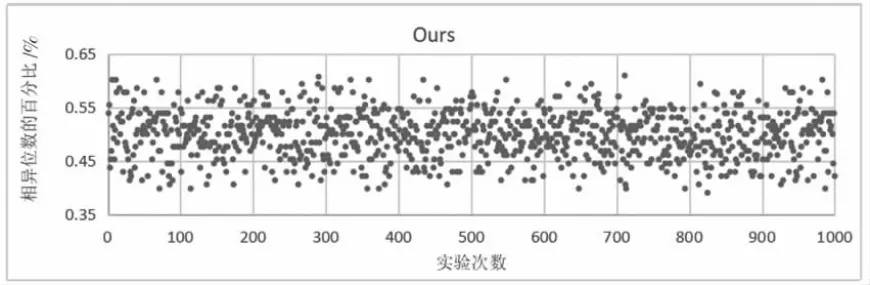
圖14 Ours 雪崩測試結果

（四）效率分析

為通過累加每次運算的時間，將時間尺度拉大，使結果便于觀察，在算法效率測試中，每個算法都需要運行10000000 次，在實驗過程中，每次輸入長度為128 bits且各不相同的消息，圖15 為效率對比結果。

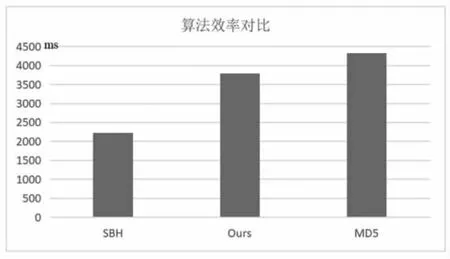
圖15 算法效率對比結果

從實驗結果可以看出，本設計提出的算法與SBH算法相比運行時間增加到了169%，與MD5 相比運行時間減少到了86.9%。由于本設計在迭代過程中引入36 步混沌映射，所以運算效率低于SBH 算法，但從結果可以看出，其依舊保留良好的密碼學算法所需的線性特性。

四、結語

本設計提出了一個針對處理短消息的哈希函數，通過引入隨機化的思想，使攻擊者在僅知到輸出結果的情況下，無法確定哈希函數的具體形式，提高了哈希函數的單向性，從而加大了攻擊難度。同時，通過多種可變參數的混沌映射，有效的解決了SBH 算法由于迭代次數過少，無法進行有效擴展的問題。由于其屬于線性運算，有效的保證了算法的運行效率。綜上所述，本設計在保證算法效率的前提下，可以有效地保障短消息在處理過程中的完整性以及安全性。