基于Gibbs 抽樣算法的兩參數Pareto分布的Bayes 估計

李凡群，韋善然

（安徽財經大學 統計與應用數學學院，安徽 蚌埠 233000）

Pareto 分布是由意大利經濟學家Pareto V 提出的收入分配理論中一個重要的分布[1]，在各個領域都被人們廣泛應用，例如城市人口容量、股票價格的波動、商業、保險等模型等都可以用Pareto 分布來進行描述，因此，研究Pareto 分布的統計性質是具有現實意義的。劉芹等[2]給出了不同損失函數下Pareto 分布參數的Bayes 估計；韓明［3］給出了Pareto 分布在尺度參數已知時，平方損失下形狀參數的E-Bayes 估計和多層Bayes 估計；朱寧［4］研究了復合MLINEX 損失函數下Pareto 分布參數的Bayes 估計，并證明了其是可容許的；楊冬霞等[5]討論了復合Mlinex 損失函數下指數威布爾分布參數的Bayes 估計；劉飛等[6]討論了基于Gibbs抽樣算法的三參數威布爾分布的Bayes 估計；喬世君等［7］討論了基于Gibbs 抽樣算法的定數截尾時威布爾分布的Bayes 估計；魏艷華［8-10］討論了基于混合Gibbs 抽樣算法的三參數威布爾分布，指數-威布爾分布和分組數據場合逆威布爾分布參數的Bayes 估計；熊常偉等[11]在熵損失函數下幾何分布可靠度的先驗分布分別為分布和冪分布時，給出了可靠度的EB 估計，并結合實際數據比較了兩種先驗分布下估計值的精度；龍兵[12]討論了雙邊定時截尾下Pareto 分布的參數估計；劉榮玄等[13]討論了三參數Pareto 分布在平方損失函數下的Bayes 估計和參數型經驗Bayes 估計等；龍兵[14]討論了雙定數混合截尾下兩參數Pareto 分布的統計分析；李鳳等[15]基于逐步增加的Ⅱ型截尾樣本,當Pareto 分布的尺度參數已知時，分別在LINEX損失和平方損失下討論了其形狀參數和可靠性指標的Bayes 估計；Pandey B N 等[16](2011)對形狀參數已知的兩參數威布爾分布的尺度參數做出了極大似然估計與Bayes 估計，并對Bayes 估計相對于極大似然估計的相對效率做了數值模擬；Saadati Nik A 等[17](2021)運用極大似然估計法、最小二乘法和貝葉斯方法（林德利近似法和馬爾可夫鏈蒙特卡洛法）估計了一種新型Pareto 分布的未知參數；Shukla G 和Kumar V[18]（2018）研究了不同先驗分布下Pareto 分布形狀參數的Bayes 估計，同時還討論了在Asymmetric Precautionary 損失函數與平方誤差損失函數下形狀參數的貝葉斯估計與極大似然估計等其它估計的比較。

本文基于Linex(Linear exponential)非對稱損失函數，給出了兩參數Pareto 分布的Bayes 估計，并且對Linex 損失函數下的Bayes 估計和極大似然估計的相對效率進行了模擬研究。

1 極大似然估計

Pareto 分布的概率密度函數表達式為

其中α是形狀參數，θ為尺度參數。

設(x1,x2,…,xn)為來自總體的獨立同分布樣本，則似然方程為

對數似然方程為

先通過極大化似然函數得

2 兩參數Pareto 分布的Bayes 估計

2.1 非正常先驗下的后驗分布

本文選取的先驗分布為非正常先驗分布：

則兩參數的后驗分布為:

其中x*=min{x1,…,xn}

2.2 基于Linex 損失函數的Bayes 估計

定義1Linex 損失函數最初是由Varian[19]提出的一種非對稱損失函數，下面給出兩參數的Linex 損失函數表達式：

定理1在Linex 損失函數(8)下，對于任一先驗分布，參數α,θ的Bayes 估計分別為：

證明：設分別為α,θ的任一估計，在損失函數(8)下，對應的Bayes 風險函數為:

上式風險函數的左端E表示為關于樣本x1,x2,…,xn的聯合分布取期望，若欲求Bayes 解，則只需要極小化

接下來令

2.3 容許性

引理1[20]在給定的Bayes 決策問題中，假設對給定的先驗分布π(θ)，θ的Bayes 估計δB(x)是唯一的，則它是容許的。

2.4 Gibbs 抽樣

MCMC 中的Gibbs 抽樣算法最初是由Geman 夫婦于1984 年提出的，并且Gibbs 抽樣算法常適用于高維隨機變量的模擬，本文將采用Gibbs抽樣算法應用于Bayes 估計。

為了能夠順利的使用Gibbs 抽樣算法從后驗分布中進行抽樣，首先需要得到兩個滿條件分布來作為轉移概率。根據后驗分布(7)，可計算出滿條件分布：

從上面兩個滿條件分布可以看到，第一個滿條件分布服從為伽馬分布，進行抽樣并不困難，而對于第二個滿條件分布則利用以下逆變換方法進行采樣。

逆變換：定義一個分布Mono(a,b)，其中a＞0,b＞0，擁有如下概率密度函數

并且對于0 ＜x＜b，分布函數為

在0 ＜x＜b上求分布函數F的逆：

因此，我們即可通過U～Uniform(0,1) 從Mono(a,b)中進行采樣，令X=bU1/a（事實上，這是Pareto 分布的倒數，如果X～Pareto(α,θ)，那么，反之亦然。）

于是得到兩個滿條件分布分別服從：

3 模擬研究

在模擬研究中，首先通過R 軟件中的actuar包生成了服從Pareto 分布的隨機樣本，并基于這些隨機樣本比較了極大似然估計與Bayes 估計的相對效率。樣本容量分別為n=1 050 100。在比較形狀參數α的相對效率時，α選取了1.5 至4，步長設置為0.25，θ=1；而在比較尺度參數θ的相對效率時，α=1.5，θ選取了1 至4，步長設置為0.2。對于Linex 非對稱損失函數的尺度參數a，在模擬形狀參數θ的相對效率時，選取了a=1,2,-1,-2 分別代表高估和低估的權重；在模擬尺度參數θ的相對效率時，選取了a=1,-1 分別代表高估和低估的權重。迭代次數M為1 000。

形狀參數與尺度參數的風險分別為：

于是兩參數Pareto 分布在Linex 損失下的Bayes 估計相對于極大似然估計的相對效率分別記為：

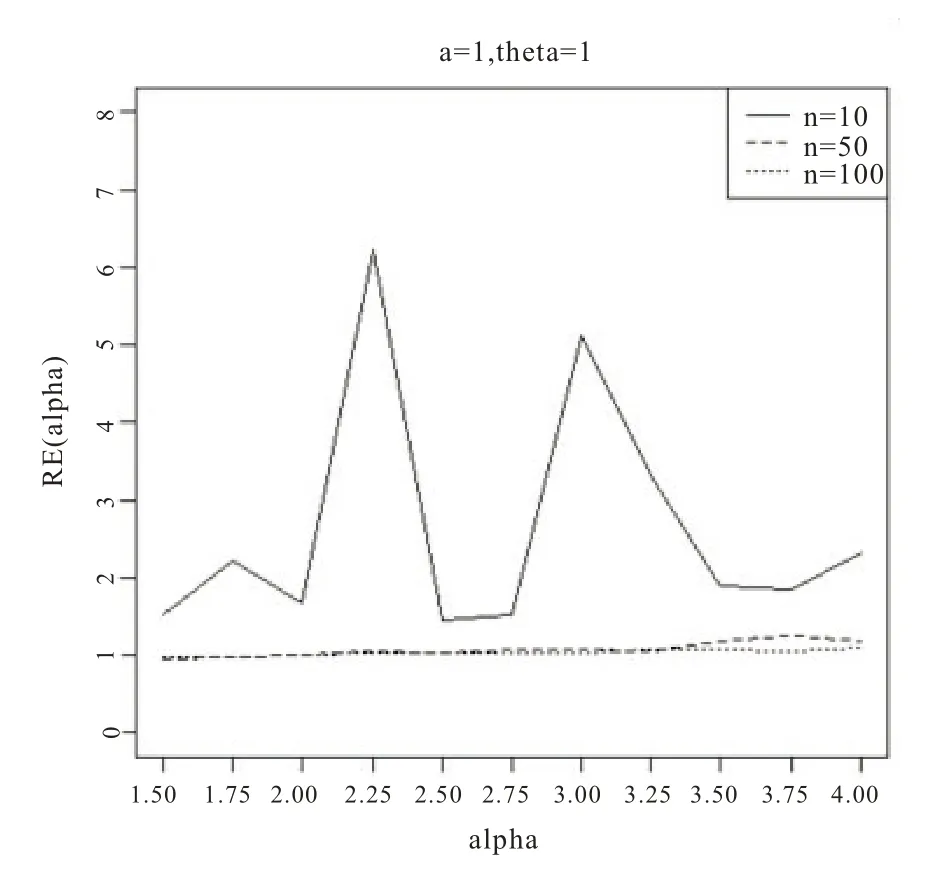
圖1 基于a=1,θ=1

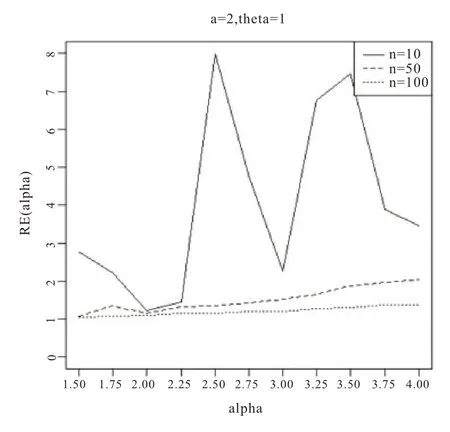
圖3 基于a=2,θ=1

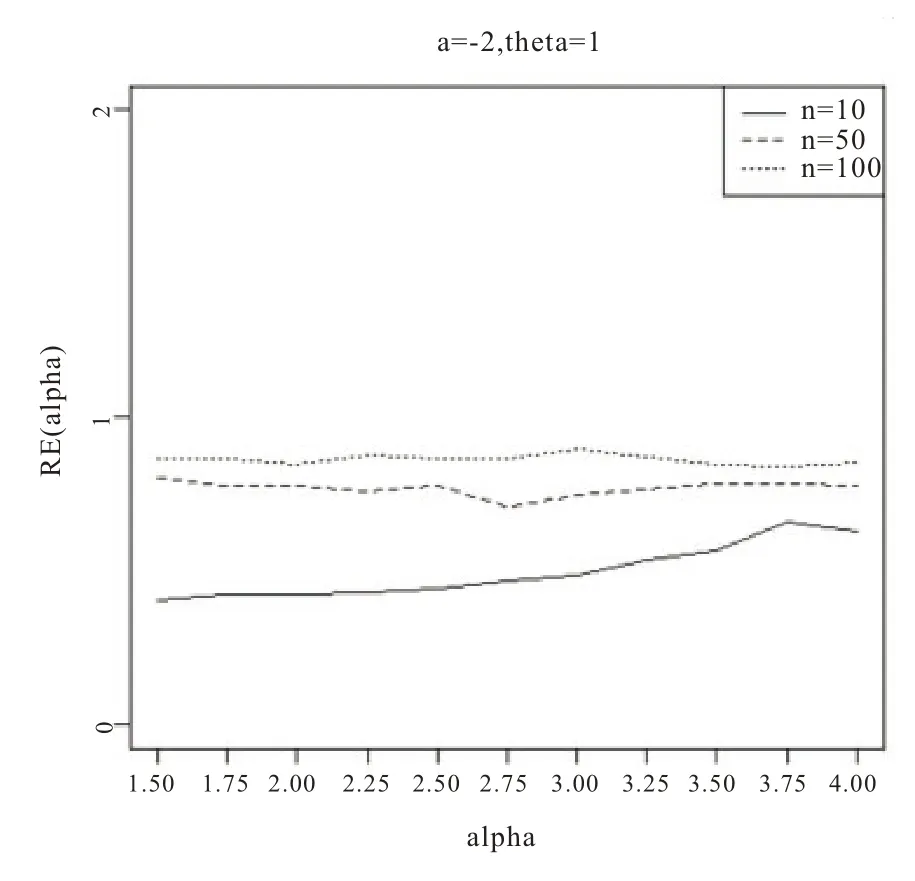
圖4 基于a=-2,θ=1

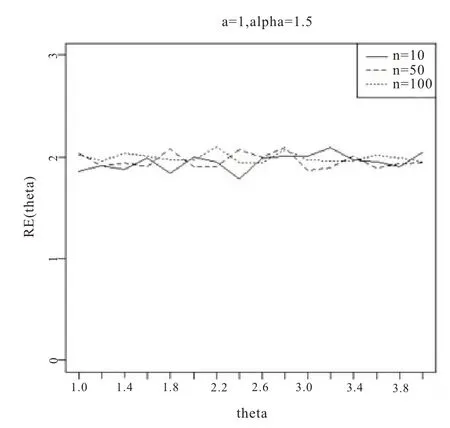
圖5 基于a=1,θ=1.5

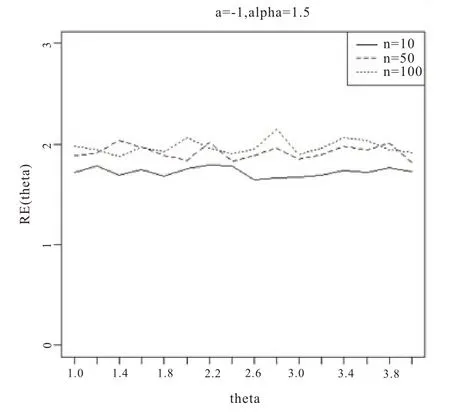
圖6 基于a=-1,α=1.5

從圖1-6 的結果表明，尺度參數θ的Bayes 估計效率要一致高于極大似然估計；而對于形狀參數a：當a＞0 時，即高估的權重大于低估時，在小樣本的情況下，Bayes 估計的效率要高于極大似然估計，而隨著樣本量的增加，兩種估計方法的效率逐漸趨于相同；當a＜0 時，即低估的權重大于高估時，在小樣本的情況下，極大似然估計的效率要高于Bayes 估計，而隨著樣本量的增加，兩種估計方法的效率也趨于相同。

4 結論

本文首先給出了兩參數Pareto 分布的極大似然估計，然后給出了基于Linex 損失函數下兩參數Pareto 分布的Bayes 估計，并利用Gibbs 抽樣算法進行了Bayes 估計實現，最后對兩者估計的相對效率進行了數值模擬。結果表明尺度參數θ的Bayes 估計效率一致高于極大似然估計；在小樣本情形下，當損失函數的尺度參數大于0 時，形狀參數α的Bayes 估計的效率高于極大似然估計。所以在小樣本情形下，對于形狀參數與尺度參數的估計，Bayes 估計的效率是要明顯優于極大似然估計的。事實上，在我們的現實生活當中，可能會經常出現一些高估比低估更關鍵的情形，并且高估應該被賦予更高的權重。例如，當分析一個地區的城市人口容量時，若大量的進行模擬研究，會給相關統計部門帶來相當大的負擔，因此在這些情形下，我們會盡可能的使用小樣本。基于這些適用于小樣本的情形，建議可在這些場景中使用Bayes 估計。