基于CFD-DPM方法的通風速度對煤塵擴散影響分析

李世民

(山西煤炭進出口集團蒲縣豹子溝煤業公司,山西 臨汾 041204)

0 引言

在未來幾十年里,煤炭仍將在我國能源結構中占主體地位[1]。目前,我國90%以上的煤炭采用地下開采方法生產[2]。隨著機械化的發展,煤炭的勘探效率大大提高。然而,在煤炭開采過程中會產生大量的煤塵顆粒。根據現有的現場實測數據,煤礦巷道中煤塵顆粒濃度可能高達2 000 mg/m3,且目前尚無有效的防塵措施。以往的研究數據顯示,煤礦巷道產生的煤塵中,采煤巷道產生的煤塵占全部煤塵的80%以上[3]。這種高濃度的煤塵顆粒不僅危害到礦工的健康,而且大大增加了煤塵爆炸的可能性[4]。高揚塵濃度的安全風險會大大增加,對煤礦環境和安全構成潛在的嚴重威脅。研究發現,隨著煤塵濃度的增加,煤塵爆炸壓力和爆炸指標呈現先上升后下降的趨勢[5]。據統計,我國532個重點煤礦中存在煤塵爆炸危險的占87.32%。此外,在煤礦巷道中完成的生產工作通常是為進一步挖掘工作面的開采做準備。因此,巷道的運行效率將直接決定開采工作面進度,直接影響到礦山的整體生產效率。氣流場被認為是決定煤塵顆粒擴散的主要因素。研究發現,合理調整風量可以有效緩解煤礦煤塵問題[6]。因此,研究強制通風氣流對綜采工作面煤塵污染特性的影響,對于改進目前采用的防塵處理方法具有重要意義。

數值模擬是一種有效且操作性強的方法,現已廣泛應用于煤礦巷道氣固流動的研究[6]。例如,WANG等[7]基于CFD研究了掘進巷道約束壁面射流通風系統的氣流分布。趙雷雨等[8]利用CFD軟件模擬煤礦工作面煤塵分布和風流行為。KURNIA等[9]將CFD模型和歐拉-拉格朗日方法相結合,研究了地下礦井中煤塵顆粒的軌跡。巫宗賓等[10]利用CFD模型研究了煤礦綜放工作面呼吸性煤塵運動和流動規律。HUA等[11]利用FLUENT方法研究了煤礦巷道2種典型通風方式下的礦塵污染特征。為此,采用離散相模型(DPM)和計算流體力學(CFD)軟件,研究不同通風速度條件下煤礦巷道內煤塵的擴散和流場特征,并通過與現場實測數據的對比,來驗證數值模擬結果的可靠性。

1 數學模型及模型構建

1.1 數學模型

煤塵在煤礦巷道氣流條件下的運動稱為氣固兩相流。因此,在建立數學模型時,既要考慮氣流運動,又要考慮煤塵擴散運動。假設煤塵是由不同大小的球形顆粒組成,將煤塵顆粒作為離散介質處理,將氣流視為連續介質,忽略傳熱和傳質。如前所述,采用歐拉-拉格朗日方法建立數學模型[12]。

1.1.1 氣流數學模型

氣流的連續性方程為

(1)

式中,ρ為空氣密度,kg/m3;ui為x、y或z方向的空氣速度,m/s;xi為x、y、z、m方向上的坐標。

由于假設氣體是不可壓縮的,根據Navier-Stokes方程,氣流動量方程可以寫成

(2)

式中,p為湍流有效壓力,Pa;μ為層流黏度系數,Pa·s;μt為湍流黏度系數,Pa·s。

μt可表示為

μt=pCμk2/ε

(3)

k方程為

(4)

ε-方程為

(5)

式中,ε為湍動能耗散速度,m2/s-3;k為湍流動量,m2/s2;Cμ,σk,σε,C1ε和C2ε分別為0.09,1.00,1.30,1.44和1.92。

1.1.2 煤塵數學模型

塵流中單個塵粒所受的力是復雜的,包括重力、拖曳力、馬格努斯力、薩弗曼力、黏附力、浮力、巴塞特力和假質量力等。一般來說,其他力比重力和拖曳力小得多,所以可以忽略不計。根據牛頓第二運動定律,作用在煤塵顆粒上的總力為[13]

(6)

式中,mp為煤塵顆粒質量,kg;up向上為煤顆粒的速度,m/s;Fd為顆粒上的阻力,N;Fg為重力,N。因此,Fd可以表示為

(7)

式中,dp為顆粒直徑,m;u為風速,m/s;up為粒子速度;Cd為阻力系數,可表示為：Cd=a1+a2/Re+a3/Re,其中a1,a2,a3為常數;Re為雷諾數,可以表示為Re=ρdp|up-u|。

1.2 物理模型和邊界條件

選取山西長治張村煤礦2601綜采工作面作為物理原型,如圖1所示。由圖可知,巷道為正長方體30.0 m×5.0 m×3.5 m(長×寬×高)。有一個掘進機、橋梁轉移機、皮帶輸送機、壓力風筒包括在模型中。進塵口位于切割頭與掘進面接觸處,進塵口的寬度和高度分別為0.65 m和0.35 m。

同時,x軸正方向從掘進工作面指向巷道末端;y軸正方向從壓力風筒所在的巷道壁面指向掘進機;z軸的正方向從地板指向巷道頂部。物理模型的參數設置見表1。

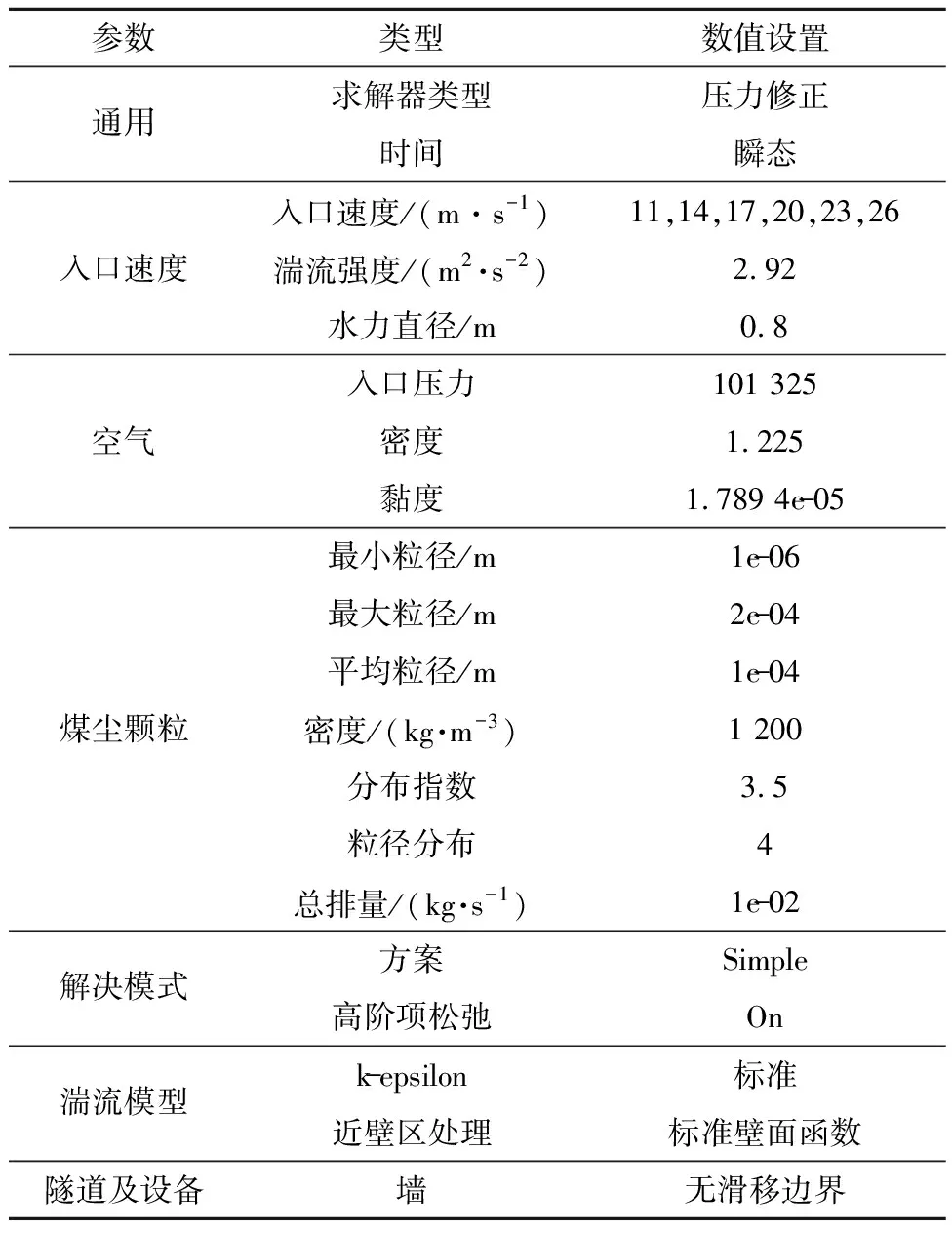
表1 計算模型參數

2 數值模擬結果分析

設通風速度V分別為11 m/s、14 m/s、17 m/s、20 m/s、23 m/s和26 m/s。

2.1 氣流遷移分析

氣流場遷移如圖2所示,各截面平均氣流速度如圖3所示。

圖2 煤礦巷道氣流場遷移圖Fig.2 Airflow field migration of coal mine roadway

由圖3可知,由于在計算域所有固體表面均施加無滑移邊界條件時巷道壁面流速為0 m /s,因此將X=0 m、X=30 m、Z=0 m、Z=3.5 m的流速分別替換為X=0.01 m、X=29.99 m、Z=0.01 m、Z=3.49 m的流速。此外,根據風流速度和風流方向的大小,將煤礦巷道沿X方向分為湍流區、回流區和穩定區。隨著通風速度的增加,各X斷面的平均風流速度增大。當通風速度不大于17 m/s時,由于過低的氣流條件攜帶的煤塵較少,X=30 m段的濃度有所增加。而當速度超過20 m/s時,氣流攜帶的煤塵速度達到平衡,因此煤塵濃度不隨X坐標變化。出現這種情況的原因是來自風筒的氣流在湍流區域的速度有所增加,而掘進機對氣流的阻塞和限制導致湍流區域氣流速度衰減加速。因此,在湍流區域內,各種通風速度的氣流均呈指數下降。由于氣流速度較小,方向相對穩定,發現再循環區氣流處于線性衰減狀態。根據風量守恒,單位時間內流出再循環區域的空氣量隨總速度的增加而增加。由于掘進機和巷道墻的限制,空間突然縮小。觀察到氣流受到空間的限制,當氣流首次進入再循環區時,無序程度迅速降低。因此,確定平均氣流在X為4～10 m時呈線性變化。掘進機區域內空間突然擴大造成局部損失,氣流速度會突然下降。但是,X為4～10 m時的氣流衰減速率明顯大于X為10～20 m時的氣流衰減速率。當氣流進入穩定區域時,氣流的方向是穩定的,并確定風流速度與巷道橫截面積及穩定區域內的通風速度呈不斷相關關系。因此,根據質量守恒定律,空氣在慣性作用下以勻速涌出巷道。

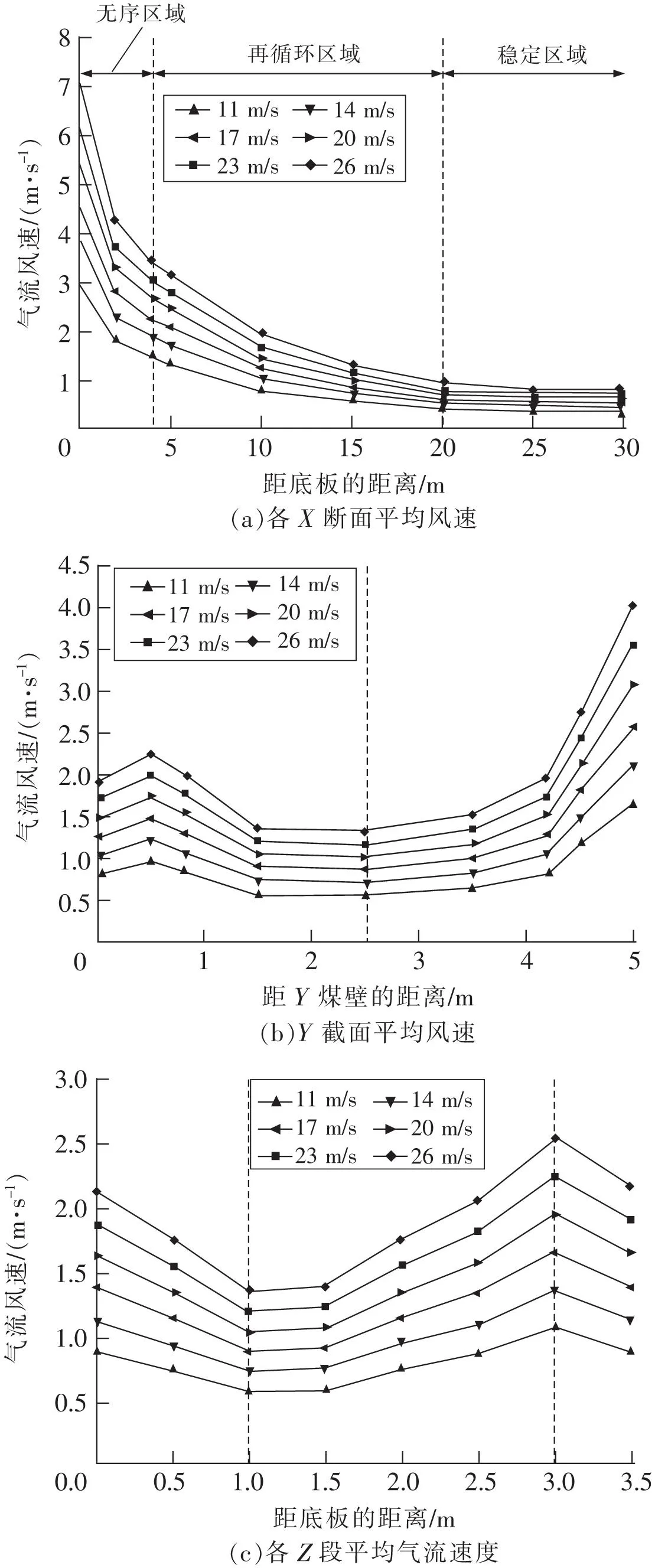
圖3 煤礦巷道各斷面平均風速Fig.3 Each section’s average ventilation velocity of coal mine roadway

不同通風速度條件下,Y截面的風速呈現出相同的變化趨勢,如圖3(b)所示。根據質量守恒定律,以時間為單位的風筒氣流增加了。因此,同一Y段的平均風速隨著通風速度的增加而增大。風筒出口在Y為0～2.5 m時,風筒排出的氣流大部分在Y為3.5～5 m時沿巷道壁向+X方向移動。其次,與迎頭相撞后,Y為3.5～5 m時的平均風速大于Y為0～1.5 m和Y為1.5～3.5 m時的平均風速。根據質量守恒,部分氣流經過掘進機,在壓力風筒出口處受夾帶作用,進入Y為0～1.5 m。這導致Y為0～1.5 m時的平均氣流速度大于Y為1.5～3.5 m時的平均氣流速度。

如圖3(c)所示,雖然速度存在差異,但Z段氣流的變化趨勢基本一致。由于風筒位置靠近巷道頂板,因此分析了從頂板到底板的氣流變化趨勢。本研究將風速的變化分為3個階段。在Z為3.5～3 m時,氣流在接近風筒出口時增加了19.29%。在Z為1～3 m時,氣流速度呈下降趨勢,這是由于在湍流區風筒外的氣流損失了大量能量所致。在Z為1.5～3 m時衰減較快,衰減速率為30.11%/m;在Z為1.5～1 m時衰減極慢,衰減率僅為6.18%。結果證實,Z為1.5～3 m時的氣流速度越高,在擾動中損失的能量越多,氣流下降的速度也越快。但在Z為1～111.5 m時氣流接近最小值,氣流趨于穩定,受擾動影響較小。根據質量守恒定律,氣流在重力作用下不斷遷移,然后向+X方向擴散。此外,風筒中的空氣在接觸掘進工作面后,直接沿掘進工作面向下擴散到巷道底板,幾乎沒有能量損失。這導致在Z為0～1 m時的氣流速度再次增加,增加了56.91%。

截面X的氣流矢量如圖4所示。在巷道兩側巷道壁的限制下,兩股氣流發生碰撞、反彈并遠離掘進工作面。圖4(a)中,在X≤4 m范圍內,由于掘進機和掘進工作面在該區域內形成相對狹窄的空間,由于夾帶作用,使得小動量空氣加速,導致該區域出現無序。從湍流區流出的氣流主要是在遠離風筒沿巷道壁、頂板回流區流動,如圖4(b)、4(c)所示。同時存在氣流渦旋場,氣流沿X軸旋轉,導致空氣流過靠近風筒的巷道壁面,繞過掘進機。然后,氣流在回流區從后向靠近掘進機風筒的一側流動。確定氣流渦旋形成的原因是掘進機左右兩側氣流流量和流速差異較大。根據伯努利定理,流體中流速越大,壓力越小。由于風筒出口處的氣流比其他區域的氣流快,因此巷道內的壓力最小。因此,觀察到風筒出口處存在射流的夾帶作用,使經過掘進機的空氣得到再循環。在穩定區域,由于氣流離風筒出口較遠,確定氣流受夾帶影響可以忽略不計。此時,高動量氣流繞帶罩旋轉,以0.5 m/s的速度流出巷道,如圖4(d)所示。

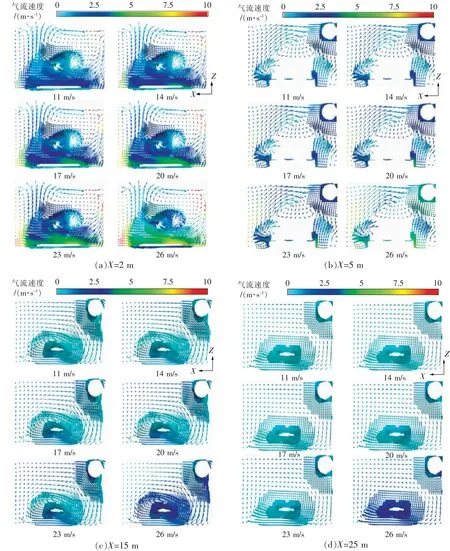
圖4 煤礦巷道X斷面氣流矢量Fig.4 X section’s airflow vector of coal mine roadway

2.2 煤塵運移

不同通風速度下巷道內煤塵運動軌跡如圖5所示。煤塵速度的間隔設置在0～5 m/s之間,便于區分煤塵速度的變化。

各斷面平均煤塵濃度如圖6所示。由于在計算域所有固體表面均施加無滑移邊界條件時巷道壁面平均煤塵濃度為0 m/s,因此將X=0 m、X=30 m、Z=0 m、Z=3.5 m的平均煤塵濃度分別替換為X=0.01 m、X=29.99 m、Z=0.01 m、Z=3.49 m的平均煤塵濃度。

煤體切割產生的煤塵在壓力筒排出的空氣的夾帶作用下,沿巷道壁面迅速移動,遠離壓力筒進入巷道出口,如圖5所示。煤塵顆粒經過掘進機后,大部分在自由擴散過程中逐漸減少,煤塵開始積累。觀察到回流帶的少量煤塵已被再循環到掘進工作面。通過分析圖5、圖6的結果,發現在湍流區X方向的煤塵濃度呈現先增加后降低的趨勢。當通風速度分別為11 m/s、14 m/s和17 m/s時,各斷面的濃度均隨通風速度的增加而降低。煤塵濃度沿X方向減小。當通風速度分別為20 m/s、23 m/s和26 m/s時,各路段的煤塵濃度均隨風速的增加而增加。這是由于當氣流速度小于17 m/s時,氣流較小,煤塵在湍流區堆積所致。但隨著氣流速度的增加,在單位時間內,湍流區煤塵顆粒的數量增大。當氣流速度不小于20 m/s時,由于通風速度的增大,夾帶作用變得明顯。

如圖6(b)所示,在通風速度為26 m/s時,除Y=0.5 m外,通風速度越高,Y方向各斷面的濃度越小。然而,當比例為26 m/s時,風筒的夾帶作用非常明顯。隨著煤塵回流速度的增大,Y=0.5 m段的煤塵濃度突然增大,如圖5(f)所示。從圖5(b)和圖6(b)可以看出,在不同風速下,Y=0.5 m處的煤塵濃度均大于Y=4.5 m處的煤塵濃度,這是由于Y=0.5 m處的氣流大于Y=4.5 m處的氣流。

圖5 煤礦巷道煤塵軌跡Fig.5 Coal dust trajectory of coal mine roadway

如圖6(c)所示,除通風速度為26 m/s時Z=3.5 m處濃度異常高外,其余Z段濃度均隨通風速度的增加而降低。這是由于當通風速度為26 m/s時,筒體出口產生了夾帶作用,在筒體出口形成了一個高含塵區。在Z為1～3.5m時,重力作用導致煤塵沉降,使得區間內的高度越小,煤塵濃度越高。

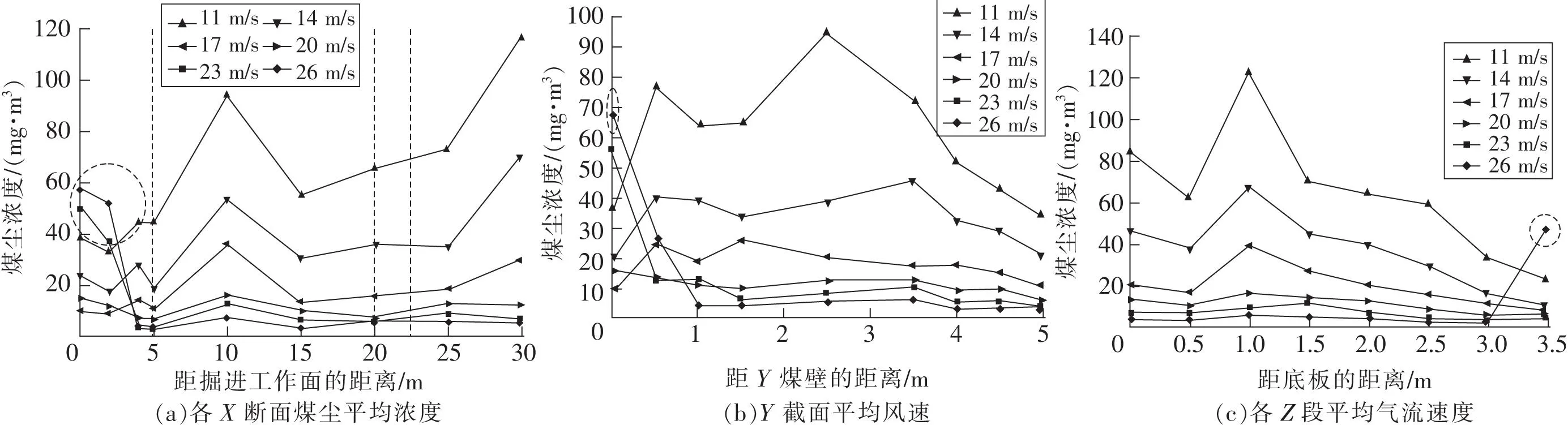
圖6 煤礦巷道各斷面煤塵平均濃度Fig.6 Each section’s coal dust average concentration of coal mine roadway

2.3 現場驗證

為了驗證模型的有效性和相關參數設置,對某煤礦巷道的現場數據進行了檢驗。測點設為1.5 m,即呼吸區高度。選取AKFC-92A礦塵采樣器和CFJ5風速儀分別測量每個測點的煤塵濃度和風速。根據現場實測數據,在開挖過程中風筒的速度為17 m/s。因此,對現場數據進行了測量,并與設定風筒速度為17 m/s時的數值結果進行對比。如圖7所示,5個測量斷面到掘進工作面的距離分別為5 m、10 m、15 m、20 m、25 m。設置這些是為了測量氣流速度和煤塵濃度。設各斷面測點坐標為：A(0.82 m,1.5 m),B(4.18 m,1.5 m)。然后,為了減少隨機誤差的可能性,連續測量煤塵濃度和氣流速度3次,并取平均值。

風速實測值和煤塵濃度的實測值、風速和煤塵濃度實測值和模擬值的標準差分別如圖8(a)和圖8(b)所示。可見,模擬的氣流速度與現場實測的速度結果基本吻合,數值模擬結果與現場實測值吻合較好。模擬風速與實際風速的平均相對誤差為4.42%。煤塵濃度模擬值與實測值的平均相對誤差為5.59%。模擬的風速和煤塵濃度與現場實測值之間的誤差較小。這些結果表明,本研究的數學模型和基本參數設置相當準確。

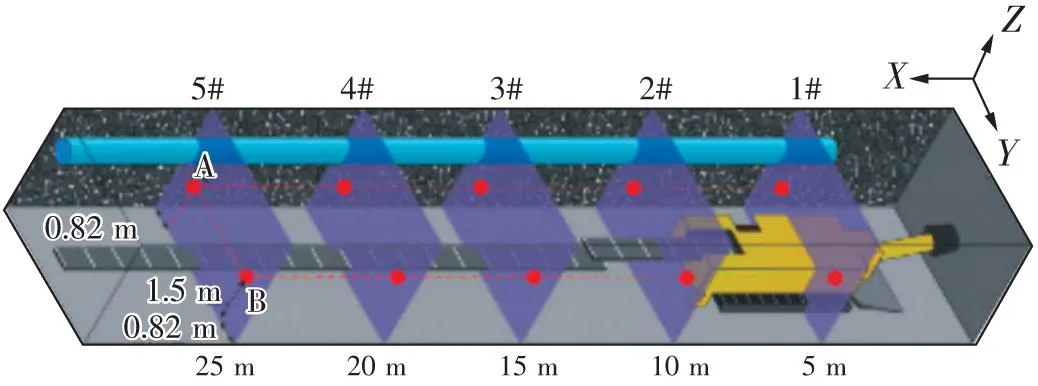
圖7 測點布置Fig.7 Layout of observing points

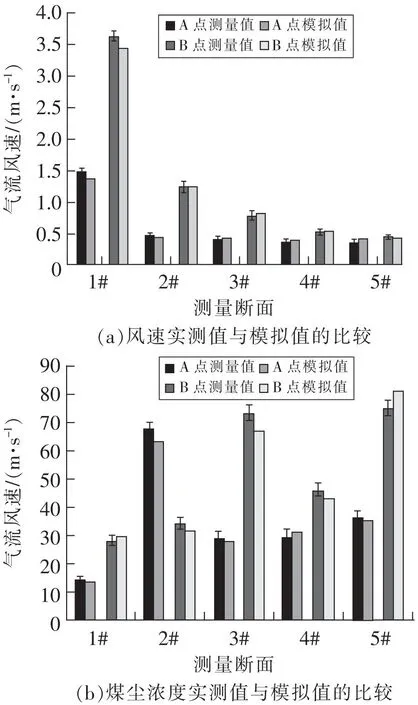
圖8 實測值與模擬值的比較Fig.8 Comparison of actually measured and simulated values

3 結論

(1)在煤礦巷道中,氣流場可分為湍流區、回流區和穩定區。巷道掘進工作面與掘進機之間存在著多個高速氣流相互作用的無序區域。在遠離風筒的沿巷道壁面的回流區域內存在較大的氣流。大部分氣流直接進入穩定區,其余氣流沿風筒同側回流進入湍流區。由于氣流在穩定區域的平穩遷移,風流速度與巷道橫截面積和通風速度呈常數關系。

(2)大部分的煤塵顆粒是通過掘進機沿巷道壁的氣流運動帶離風筒而產生的。在掘進機后方約5 m處,由于氣流速度較低,煤塵濃度突然增加,部分煤塵沉降。研究發現,大量的煤塵顆粒被帶入穩定區域,來自掘進機后部的煤塵顆粒在夾帶作用下遷移到風筒出口。

(3)當通風速度不超過17 m/s時,穩定區域的煤塵濃度呈現出突然上升的趨勢,其原因是煤塵產生速率超過了煤塵遷移速率。在風筒出口處存在明顯的煤塵堆積區,這是由于卷吸作用造成的,當通風速度超過17 m/s時,有更多的煤塵顆粒被回流帶入該區域。