基本圖形的分解與重構(gòu)能力考查：以2023年天津中考數(shù)學(xué)試題為例

馮玉嫻

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022 年版）》（以下簡(jiǎn)稱“《課標(biāo)》”）指出：初中階段“圖形與幾何”領(lǐng)域的內(nèi)容分為“圖形的性質(zhì)”“圖形的變化”“圖形與坐標(biāo)”三個(gè)主題。初中生主要學(xué)習(xí)點(diǎn)、線、面、角、三角形、多邊形和圓等幾何圖形，從演繹證明、運(yùn)動(dòng)變化、量化分析三個(gè)方面研究這些圖形的基本性質(zhì)和相互關(guān)系。“圖形的性質(zhì)”主要側(cè)重學(xué)生對(duì)圖形概念的理解，以及對(duì)基于概念的圖形性質(zhì)、關(guān)系、變化規(guī)律的理解，重點(diǎn)強(qiáng)調(diào)直觀發(fā)現(xiàn)、整體聯(lián)想、邏輯推理來(lái)研究圖形；“圖形的變化”強(qiáng)調(diào)從運(yùn)動(dòng)變化的觀點(diǎn)來(lái)研究圖形；“圖形與坐標(biāo)”強(qiáng)調(diào)數(shù)形結(jié)合，用代數(shù)方法研究幾何圖形[1]。因此，“圖形的性質(zhì)”是“圖形與幾何”領(lǐng)域的主干知識(shí)，是“圖形的變化”“圖形與坐標(biāo)”的學(xué)習(xí)基礎(chǔ)，是中考命題考查的核心內(nèi)容。中考試題中通常是以單個(gè)圖形或幾個(gè)基本圖形的組合圖形為背景，考查圖形的概念和性質(zhì)的簡(jiǎn)單應(yīng)用，注重基本圖形的性質(zhì)對(duì)圖形中相關(guān)線段、角、局部等對(duì)象進(jìn)行定性與定量的分析，以促進(jìn)學(xué)生對(duì)圖形的性質(zhì)的全面理解和整體把握[2]。2023 年天津市中考落實(shí)《課標(biāo)》的學(xué)業(yè)要求，既有傳承又有創(chuàng)新。以下通過(guò)對(duì)試卷中第（17）題和第（21）題的詳細(xì)剖析，闡述在圖形中考查學(xué)生分析和解決問(wèn)題的設(shè)計(jì)思路及分析方法。

一、試題評(píng)析

（一）關(guān)注圖形，強(qiáng)化關(guān)聯(lián)

（17）題：如圖1，在邊長(zhǎng)為3的正方形ABCD的外側(cè)，作等腰三角形ADE，且EA=ED=

（Ⅰ）△ADE的面積為__________；

（Ⅱ）若F是BE的中點(diǎn)，連接AF交CD于點(diǎn)G，則AG的長(zhǎng)為__________.

1.考查意圖解析

此題參考人教版數(shù)學(xué)教材八年級(jí)下冊(cè)第十八章平行四邊形復(fù)習(xí)題第1 題（3），將原題的等邊三角形，變?yōu)檠c底邊不相等的等腰三角形，將角的計(jì)算改為求線段長(zhǎng)的問(wèn)題，重點(diǎn)突出變中不變的規(guī)律，探尋圖形中邊、角兩個(gè)重要組成要素之間的關(guān)系。考查正方形的性質(zhì)、等腰三角形的性質(zhì)、平行線分線段成比例的基本事實(shí)、全等三角形的判定和性質(zhì)、勾股定理等數(shù)學(xué)知識(shí)，其中，靈活的運(yùn)算能力是解決此題的重要因素。

本題涵蓋正方形、等腰三角形、直角三角形、三角形的中位線、全等三角形等內(nèi)容，關(guān)注學(xué)生在復(fù)雜圖形中分解出基本圖形的能力，是對(duì)學(xué)生的識(shí)圖能力、推理能力的綜合考查。強(qiáng)調(diào)了基本圖形的基本性質(zhì)、探究圖形的基本要素之間的內(nèi)在聯(lián)系，這樣有助于學(xué)生合理選擇數(shù)學(xué)方法，養(yǎng)成良好的思維品質(zhì)。抓住“關(guān)鍵要素”，探究相關(guān)聯(lián)系是解決本題的重要思路。這樣的設(shè)計(jì)，主要考查圖形的主要要素之間的位置關(guān)系和數(shù)量關(guān)系，學(xué)生需要在新的圖形情境中，借助幾何直觀分析問(wèn)題。本題給學(xué)生預(yù)留很大的探索空間，學(xué)生在解決問(wèn)題的過(guò)程中，可以體會(huì)多角度思考問(wèn)題，發(fā)展推理能力。

2.解法分析

第（Ⅰ）問(wèn)求△ADE的面積，需要求等腰△ADE底邊的高EM，而EM在Rt△AME中，運(yùn)用勾股定理得到EM=2。體現(xiàn)了等腰三角形中“見等腰作底邊上的高”的通性通法。

第（Ⅱ）問(wèn)求線段AG的長(zhǎng)，首先考慮所求線段在什么圖形中研究。按照“它是誰(shuí)，在哪，與誰(shuí)有關(guān)系”三個(gè)層次的思維方式思考，也就是說(shuō)，所求的線段是哪個(gè)圖形的組成要素，能在這個(gè)圖形中求解嗎？若圖形的已知條件滿足，可以直接求解；若已知條件不足，可以將缺少的要素轉(zhuǎn)化至另一個(gè)可以求解的圖形中。

【思路一：直擊目標(biāo)】

常見的分析方法是“執(zhí)果索因”，即要求線段AG的長(zhǎng)，發(fā)現(xiàn)圖中AG在Rt△AGD中，AD的長(zhǎng)是已知條件，因此轉(zhuǎn)化為求GD的長(zhǎng)的問(wèn)題。

【方法1：借助軸對(duì)稱構(gòu)造全等三角形】

如圖2，過(guò)點(diǎn)E作EM⊥AD，延長(zhǎng)EM交AG于點(diǎn)N，由平行線分線段成比例的基本事實(shí)可知GD=2MN，轉(zhuǎn)化為求MN的長(zhǎng)。由F是BE中點(diǎn)，可以聯(lián)想到△ABF≌△NEF，得到NE=AB=3，從而得出MN=1，進(jìn)而計(jì)算出GD=2，由勾股定理得AG=。解決本題的關(guān)鍵是發(fā)現(xiàn)由正方形和等腰三角形組合而成的整體圖形是軸對(duì)稱圖形，EM所在直線是對(duì)稱軸，將第（Ⅰ）問(wèn)和第（Ⅱ）問(wèn)巧妙地建立聯(lián)系，體現(xiàn)最優(yōu)化最簡(jiǎn)潔的解題思路。

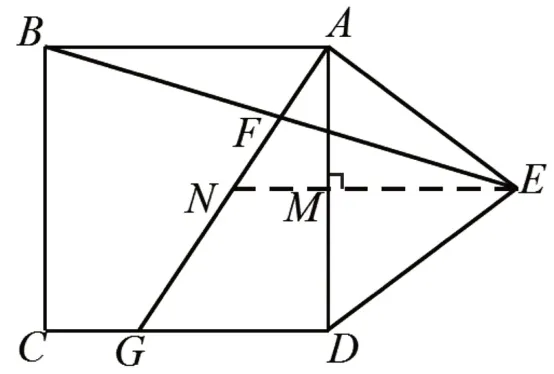
圖2

【方法2：借助中點(diǎn)構(gòu)造三角形的中位線】

如圖3，由中點(diǎn)F，聯(lián)想AF是哪個(gè)三角形的中位線。延長(zhǎng)BA，使AH=BA=3，連接HE。將問(wèn)題轉(zhuǎn)化為關(guān)鍵點(diǎn)E與誰(shuí)有關(guān)？分別延長(zhǎng)HE和AE，與CD的延長(zhǎng)線分別相交于點(diǎn)M、N。發(fā)現(xiàn)在Rt△ADN中，點(diǎn)E是斜邊AN的中點(diǎn)，根據(jù)勾股定理得于是有△AEH≌△NEM，可知MN=3。由四邊形AGMH是平行四邊形可知GM=AH=3，從而計(jì)算出GD=2。回到基本圖形Rt△AGD中，得這種方法看似煩瑣，但是學(xué)生能從中點(diǎn)出發(fā)構(gòu)造基本圖形的思維方法是有意義的，凸顯在復(fù)雜圖形中識(shí)別基本圖形的能力。

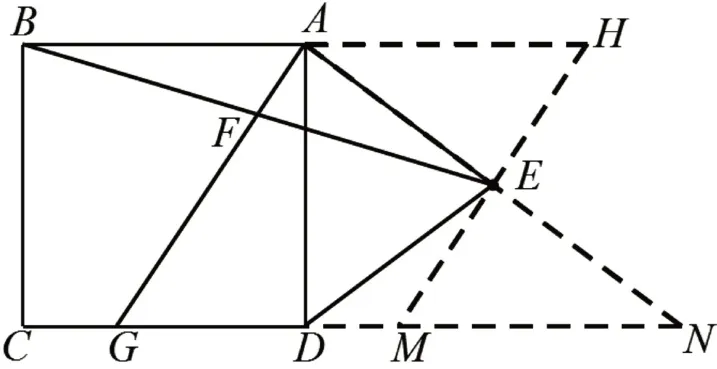
圖3

【方法3：構(gòu)造相似三角形】

如圖4，由關(guān)鍵點(diǎn)E聯(lián)想到構(gòu)造相似三角形。延長(zhǎng)CD、BE交于點(diǎn)H，點(diǎn)E作EM⊥CH，垂足為M。由BH。由AB∥GH得△ABF∽△GHF，有得GH=9。因?yàn)镋M∥BC得△HEM∽△HBC，有得到MH=5，從而計(jì)算出GD=2，從而計(jì)算出有的學(xué)生對(duì)平行線分線段成比例的基本事實(shí)和相似三角形情有獨(dú)鐘，善于靈活運(yùn)用到解題中，積累了豐富的數(shù)學(xué)活動(dòng)經(jīng)驗(yàn)，體現(xiàn)學(xué)生思維的廣闊性。

圖4

【教學(xué)建議】教學(xué)中，教師應(yīng)引導(dǎo)學(xué)生發(fā)現(xiàn)圖形的對(duì)稱特點(diǎn)，幫助學(xué)生學(xué)會(huì)用整體的、聯(lián)系的、發(fā)展的眼光看問(wèn)題。運(yùn)用第一種方法解決問(wèn)題，凸顯通性通法的重要性，這是中考考查的重點(diǎn)。學(xué)生只有積累了豐富的解題經(jīng)驗(yàn)，才能在中考答題時(shí)游刃有余，避免將簡(jiǎn)單的問(wèn)題復(fù)雜化。

【思路二：樹木成林】

由樹木見森林，由部分看整體是一種解題策略。AF是AG的一部分，可將求AG的長(zhǎng)轉(zhuǎn)化為求AF的長(zhǎng)，或者轉(zhuǎn)化為求AG的長(zhǎng)。

【方法1：借助線段的倍分關(guān)系求解】

由于學(xué)生的思維存在差異，對(duì)于中點(diǎn)F所處的位置會(huì)產(chǎn)生不同的聯(lián)想。如圖2，發(fā)現(xiàn)AG=2AN，于是轉(zhuǎn)化為求AN的長(zhǎng)。在Rt△AMN中，由MN=1，AM=計(jì)算得，推出

【方法2：借助比例關(guān)系求解】

有的學(xué)生發(fā)現(xiàn)AG=AF+FG，重新構(gòu)造新的直角三角形，分別求AF，F(xiàn)G的長(zhǎng)。見到中點(diǎn)F，想到構(gòu)造三角形的中位線是一種常見的思維方法。

如圖5，過(guò)點(diǎn)作FM⊥BA，垂足為M。延長(zhǎng)MF交CD于點(diǎn)N，過(guò)點(diǎn)作EH⊥BA，與BA的延長(zhǎng)線交于點(diǎn)H。由根據(jù)勾股定理得。由AM∥GN得所以FG=3AF，進(jìn)而AG=AF+FG=4AF=

圖5

【教學(xué)建議】教學(xué)中，教師應(yīng)善于拓寬學(xué)生的解題思路，引導(dǎo)學(xué)生從多角度思考問(wèn)題，從整體問(wèn)題的一部分切入，也是一種常見的思維方法。“借助線段倍分關(guān)系求解”與思路一“借助軸對(duì)稱構(gòu)造全等三角形”有異曲同工之處，區(qū)別在于放在不同的直角三角形求線段的長(zhǎng)，體現(xiàn)直接求解和間接求解各自的優(yōu)勢(shì)，學(xué)生應(yīng)該具備優(yōu)化解題思路的能力。

【思路三：創(chuàng)設(shè)情境】

借助圖形的特征，建立平面直角坐標(biāo)系，將“圖形的性質(zhì)”轉(zhuǎn)化為“圖形與坐標(biāo)”的問(wèn)題，運(yùn)用幾何直觀，從“形”和“數(shù)”兩個(gè)方面進(jìn)行思考，將求AG的長(zhǎng)轉(zhuǎn)化為求點(diǎn)A與點(diǎn)G之間的距離。

如圖6，以C為原點(diǎn)，CD所在直線為x軸，CB所在直線為y軸。易得點(diǎn)，由于直線AF：y=kx+b過(guò)點(diǎn)A（3，3）、點(diǎn)，所以有

圖6

這種解題思路對(duì)于初中生不常見，當(dāng)學(xué)生發(fā)現(xiàn)圖形形狀的特殊性，且在平面直角坐標(biāo)系中可以用坐標(biāo)表示圖形中點(diǎn)A、B、E的位置，學(xué)生能理解平面上的點(diǎn)與坐標(biāo)之間的一一對(duì)應(yīng)關(guān)系，才能想到用代數(shù)方法研究幾何圖形。在具體問(wèn)題情境中，學(xué)生會(huì)從代數(shù)的角度分析和解決幾何問(wèn)題，體現(xiàn)數(shù)形結(jié)合思想，用坐標(biāo)法分析和解決問(wèn)題，是發(fā)展幾何直觀和創(chuàng)新意識(shí)的途徑之一。

（二）多解歸一，探尋本質(zhì)

（21）在⊙O中，半徑OC垂直于弦AB，垂足為D，∠AOC=60°，E為弦AB所對(duì)的優(yōu)弧上一點(diǎn).

（Ⅰ）如圖7，求∠AOB和∠CEB的大小；

圖7

（Ⅱ）如圖8，CE與AB相交于點(diǎn)F，EF=EB，過(guò)點(diǎn)E作⊙O的切線，與CO的延長(zhǎng)線相交于點(diǎn)G.若OA=3，求EG的長(zhǎng).

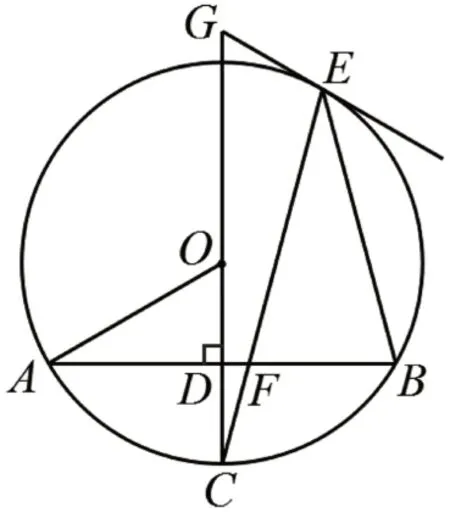
圖8

1.考查意圖解析

此題參考人教版數(shù)學(xué)教科書九年級(jí)上冊(cè)習(xí)題24.1 第5 題，已知垂直于弦的半徑，由圓心角的度數(shù)求出另一個(gè)圓心角∠AOB的度數(shù)和圓周角∠CEB的度數(shù)。題目中的點(diǎn)D是垂足，也是弦AB的中點(diǎn)，點(diǎn)E為弦AB所對(duì)的優(yōu)弧上一點(diǎn)，將圖7 和圖8 有機(jī)融合，建立聯(lián)系。又將問(wèn)題拓展為直線與圓相切的位置關(guān)系，以切點(diǎn)為頂點(diǎn)構(gòu)造等腰三角形BEF，從而求切線長(zhǎng)GE。

本題將圓與等腰三角形、直角三角形有機(jī)結(jié)合，是一道以圓的有關(guān)知識(shí)為基礎(chǔ)的幾何圖形計(jì)算題，考查學(xué)生的識(shí)圖能力、幾何直觀、推理能力。本題結(jié)構(gòu)鮮明，思路順暢，重點(diǎn)考查圓周角定理、切線的性質(zhì)、等腰三角形的性質(zhì)、直角三角形的性質(zhì)、三角形內(nèi)角和定理、解直角三角形等知識(shí)。

2.解法分析

第（Ⅰ）問(wèn)求角的度數(shù)，首先分析∠AOB是圓心角，是已知的圓心角∠AOC的2 倍，所求的圓周角∠CEB與圓心角∠BOC對(duì)著同一條弧，容易解決問(wèn)題。

【思路一：“圓”來(lái)如此】

垂徑定理是解決問(wèn)題的關(guān)鍵，圓是一種曲線圖形，它既是軸對(duì)稱圖形又是中心對(duì)稱圖形，因此借助圓的性質(zhì)就能解決問(wèn)題。由垂徑定理得在同圓中，如果兩條弧相等，那么它們所對(duì)的圓心角相等，所以得出∠AOC=∠BOC，進(jìn)而得出∠AOB=2∠AOC=120°，根據(jù)圓周角定理有∠CEB=30°。

【思路二：對(duì)稱之美】

由于等腰三角形是軸對(duì)稱圖形，探究得到等腰三角形的性質(zhì)，它是解決本題的關(guān)鍵。由等腰三角形AOB的“三線合一”可知∠AOC=∠BOC，易得∠AOB=2∠AOC=120°，從而求出30°。

對(duì)比兩種思路，圖7 中兩個(gè)基本圖形垂徑定理和等腰△AOB都能求∠AOB的度數(shù)，再運(yùn)用圓周角定理求圓周角∠CEB的度數(shù)。第（Ⅰ）問(wèn)重點(diǎn)考查基礎(chǔ)知識(shí)和基本圖形，學(xué)生可以從不同的角度思考，很容易求解。

第（Ⅱ）問(wèn)求線段GE的長(zhǎng)，GE在△GCE中無(wú)法求解，需要重新構(gòu)造基本圖形，將問(wèn)題層層轉(zhuǎn)化。GE是圓的切線，依據(jù)切線的性質(zhì)，自然想到“見切線連半徑”，連接OE有OE⊥GE。在Rt△OEG中，已知半徑OE=3，斜邊OG不可求，問(wèn)題轉(zhuǎn)化為求∠GOE或∠G的大小。問(wèn)題逐步轉(zhuǎn)化，由“要知”思考到“需知”，思路自然順暢，合情合理[3]。

【思路一：自“圓”其說(shuō)】

借助圓周角∠C求圓心角∠GOE的大小，這是圓中求圓心角的通性通法。

【方法1：運(yùn)用等腰三角形的“等邊對(duì)等角”求圓周角∠C】

如圖9，等腰三角形的頂角和底角是重要要素，等腰三角形的兩個(gè)底角相等，所以由頂角的度數(shù)知底角的度數(shù)，有∠EFB=75°，看到圖中∠DFC和∠EFB是對(duì)頂角，問(wèn)題轉(zhuǎn)化為Rt△CDF中兩個(gè)銳角互余，求得∠C=15°。由 圓 周 角 定 理 得∠GOE=2 ∠C=30°。∠GOE既是圓心角，又是直角三角形的一個(gè)銳角，架起兩個(gè)圖形之間的橋梁。在Rt△OEG中，tan∠GOE=

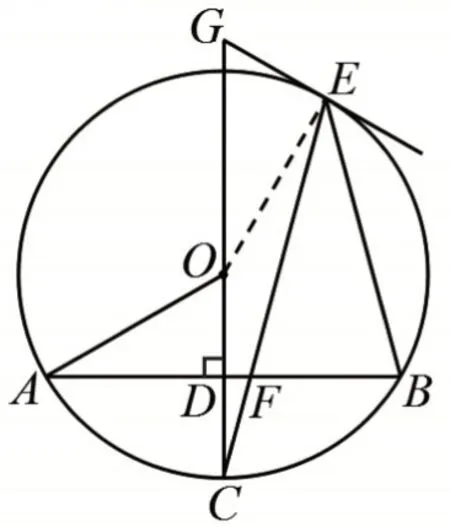
圖9

【方法2：運(yùn)用等腰三角形的“三線合一”求圓周角∠C】

如圖10，連接OE，過(guò)點(diǎn)E作EM⊥FB，垂足為M。等腰三角形底邊上的高、底邊上的中線、頂角的平分線互相重合，可知已知OC⊥AB，有OC∥EM，所以∠C=∠FEM=15°，進(jìn)而∠GOE=2∠C=30°，所以

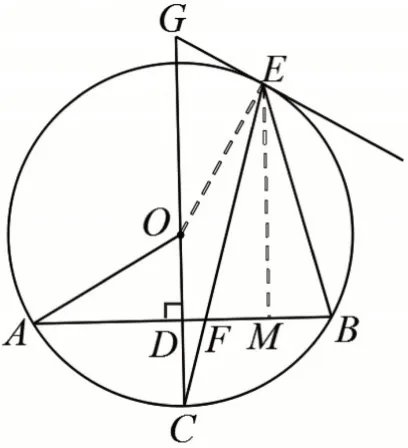
圖10

【思路二：積沙成塔】

運(yùn)用圓心角的和差關(guān)系求角，就是把相關(guān)的角逐一求出，最后運(yùn)用這些角的位置關(guān)系和數(shù)量關(guān)系解決問(wèn)題。

【方法1：圓周角是橋梁】

如圖9，等腰三角形BEF的兩個(gè)底角相等，求得∠EBF=∠EFB=75°。根據(jù)圓周角定理可知∠AOE=2∠EBF=150°，所以有∠GOE=∠AOE-∠AOG=30°，所以

【方法2：等腰直角三角形是橋梁】

如圖11，連接OE、OB，易得∠OBE=∠EBF-∠OBF=45°，發(fā)現(xiàn)△BOE是等腰直角三角形，得∠BOE=90°，從而得到∠GOE=180°-∠BOE-∠COB=30°，所以EG=。輔助線OB將第（Ⅱ）問(wèn)的圖形轉(zhuǎn)化為第（Ⅰ）問(wèn)的圖形，第（Ⅰ）問(wèn)中的結(jié)論和解題方法是第（Ⅱ）問(wèn)的基礎(chǔ)和延續(xù)，讓兩個(gè)問(wèn)題相輔相成、相得益彰。

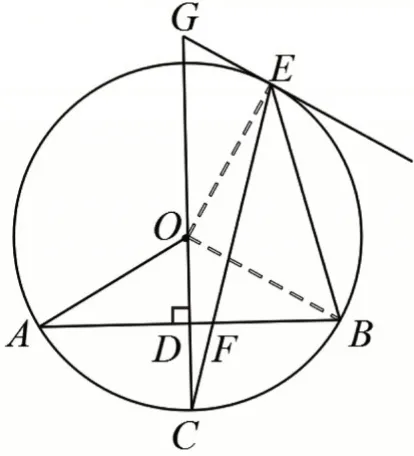
圖11

【方法3：四邊形是橋梁】

如圖11，在四邊形DBEG中，∠GDB=90°，∠DBE=75°，∠GEB=∠GEO+∠BEO=135°，可得∠G=60°，所以

【教學(xué)建議】基本圖形在數(shù)學(xué)解題中有著舉足輕重的作用，由于學(xué)生的知識(shí)儲(chǔ)備、思考問(wèn)題的方式不同，所以學(xué)生解決問(wèn)題的策略和方向也就不同。從一題多解到多解歸一，使解題經(jīng)驗(yàn)升華到系統(tǒng)思維高度。教師要理解學(xué)生的所思所想，秉承“不同的人在數(shù)學(xué)上得到不同的發(fā)展”的數(shù)學(xué)課程基本理念，為不同學(xué)生的多樣性發(fā)展提供空間[4]。這樣的題目設(shè)計(jì)采用經(jīng)典圖形，注重學(xué)生對(duì)所學(xué)基礎(chǔ)知識(shí)的理解，讓學(xué)生體會(huì)數(shù)學(xué)知識(shí)之間的聯(lián)系，發(fā)展幾何直觀和推理能力。

二、教學(xué)啟示

（一）夯實(shí)基礎(chǔ)，培養(yǎng)識(shí)圖能力

掌握好基礎(chǔ)知識(shí)、基本技能是從事高水平數(shù)學(xué)活動(dòng)的保證，為學(xué)生形成高階思維奠定堅(jiān)實(shí)的基礎(chǔ)。“圖形的性質(zhì)”強(qiáng)調(diào)通過(guò)實(shí)驗(yàn)探究、直觀發(fā)現(xiàn)、推理論證來(lái)研究圖形，學(xué)生應(yīng)經(jīng)歷知識(shí)的發(fā)生、發(fā)展過(guò)程，明確“為什么學(xué)？”“是什么？”“有什么用？”“怎么用？”如，第（17）和（21）題中涉及的基礎(chǔ)知識(shí)覆蓋初中學(xué)段“幾何與圖形”領(lǐng)域的核心內(nèi)容，涵蓋三角形、四邊形和圓等相關(guān)知識(shí)，學(xué)生應(yīng)結(jié)合基本圖形，從文字語(yǔ)言、符號(hào)語(yǔ)言和圖形語(yǔ)言描述概念和性質(zhì)。學(xué)生通過(guò)對(duì)第（17）和（21）題的圖形結(jié)構(gòu)進(jìn)行再認(rèn)識(shí)、新構(gòu)思，才能形成解題策略。因此，教學(xué)中關(guān)注學(xué)生“怎樣想到的”比“怎樣解決的”更為重要。教師應(yīng)幫助學(xué)生梳理知識(shí)結(jié)構(gòu)，讓知識(shí)之間建立聯(lián)系，形成知識(shí)體系，加強(qiáng)核心知識(shí)的研究，理解并掌握通性通法。既要培養(yǎng)學(xué)生注重對(duì)基本圖形的形的提煉、辨認(rèn)、分離、聯(lián)想和重構(gòu)，也要注重培養(yǎng)學(xué)生對(duì)基本圖形的探索、理解、詮釋、感悟和內(nèi)化，這樣才能使學(xué)生的解題能力得到實(shí)質(zhì)性的提升。

（二）積累經(jīng)驗(yàn)，重視一般觀念引領(lǐng)

章建躍博士說(shuō)，數(shù)學(xué)教材的體系結(jié)構(gòu)遵循“一定之規(guī)”，一般按“背景—定義—分類—性質(zhì)—特例—聯(lián)系”的邏輯展開。一般觀念是指研究一個(gè)數(shù)學(xué)對(duì)象，首先要定義對(duì)象，再?gòu)亩x出發(fā)研究性質(zhì)。性質(zhì)要研究的問(wèn)題是對(duì)象的要素之間的關(guān)系、相關(guān)的重要元素之間的關(guān)系、對(duì)象之間的相互關(guān)系等。例如，等腰三角形是一種特殊的三角形，它除了具有一般三角形的所有性質(zhì)外，還有許多特殊的性質(zhì)，這些特殊的性質(zhì)，都和它是軸對(duì)稱圖形有關(guān)，得出“等邊對(duì)等角”“三線合一”等性質(zhì)，并進(jìn)一步討論等腰三角形的判定方法以及等邊三角形的性質(zhì)與判定方法等內(nèi)容。教學(xué)中，要重視對(duì)教學(xué)內(nèi)容的整體分析，幫助學(xué)生建立能體現(xiàn)數(shù)學(xué)本質(zhì)，整體把握學(xué)習(xí)“圖形的性質(zhì)”的主要脈絡(luò)，突出“概念—性質(zhì)—判定—聯(lián)系—應(yīng)用”的研究主線，讓學(xué)生學(xué)會(huì)從特殊到一般，從一般到特殊，從具體到抽象的探究方法，在觀察、實(shí)驗(yàn)、計(jì)算、操作、猜想、驗(yàn)證、推理中體會(huì)并運(yùn)用數(shù)學(xué)思想與方法，積累數(shù)學(xué)的基本活動(dòng)經(jīng)驗(yàn)，逐步形成核心素養(yǎng)。

（三）全面聯(lián)動(dòng)，發(fā)展思維能力

思維是數(shù)學(xué)學(xué)習(xí)的核心，是發(fā)展能力的關(guān)鍵，是數(shù)學(xué)核心素養(yǎng)的重要體現(xiàn)，數(shù)學(xué)知識(shí)及其背后蘊(yùn)含的數(shù)學(xué)思想方法，是提升和培養(yǎng)學(xué)生思維能力的重要載體。例如，第（21）題第（Ⅱ）問(wèn)求線段的長(zhǎng)，不同的學(xué)生對(duì)問(wèn)題的思考角度不相同，因此解決問(wèn)題的路徑也就不相同。學(xué)生將問(wèn)題轉(zhuǎn)化為熟悉的基本圖形，將未知轉(zhuǎn)化為已知，將復(fù)雜的問(wèn)題轉(zhuǎn)化為簡(jiǎn)單的問(wèn)題，充分體現(xiàn)轉(zhuǎn)化是初中數(shù)學(xué)的核心思想。數(shù)學(xué)思想方法是對(duì)數(shù)學(xué)知識(shí)在更高層次上的抽象和概括，它具有總結(jié)性、實(shí)用性、規(guī)律性，也具備一定的基礎(chǔ)性。數(shù)學(xué)思想的形成需要經(jīng)歷一個(gè)從模糊到清晰、從理解到應(yīng)用的長(zhǎng)期發(fā)展過(guò)程。學(xué)生只有經(jīng)歷了這樣的過(guò)程，才能深刻體驗(yàn)、感悟、內(nèi)化數(shù)學(xué)思想方法，從而真正地發(fā)展思維能力[4]。教學(xué)中，教師應(yīng)精選、整合教材中相關(guān)內(nèi)容，重視變式與創(chuàng)新，關(guān)注內(nèi)容與能力共融的綜合性問(wèn)題，鼓勵(lì)學(xué)生從多角度分析問(wèn)題、解決問(wèn)題，培養(yǎng)學(xué)生數(shù)學(xué)思維的靈活性、深刻性和廣闊性，實(shí)現(xiàn)正向遷移，觸類旁通，力求達(dá)到“做一題，會(huì)一類，通一片”的教學(xué)效果。通過(guò)一題多解、一題多變，不僅能夠有效觸發(fā)學(xué)生多角度、多方位地思考，更重要的是全面聯(lián)動(dòng)數(shù)學(xué)知識(shí)，促進(jìn)數(shù)學(xué)知識(shí)體系的有效構(gòu)建，提升關(guān)鍵能力，發(fā)展核心素養(yǎng)。

總之，在數(shù)學(xué)教學(xué)與評(píng)價(jià)中，教師應(yīng)以《課標(biāo)》為依據(jù)，在關(guān)注數(shù)學(xué)學(xué)習(xí)結(jié)果的同時(shí)，更要關(guān)注學(xué)生對(duì)思考問(wèn)題、解決問(wèn)題方法的提煉和歸納，讓學(xué)生不僅“知其然”，還要“知其所以然”，達(dá)到“何由以知其所以然”。只有這樣，學(xué)生無(wú)論遇到什么樣的新問(wèn)題和新題型，都能用數(shù)學(xué)的眼光、數(shù)學(xué)的思維、數(shù)學(xué)的語(yǔ)言從容應(yīng)對(duì)，進(jìn)一步發(fā)展推理能力和運(yùn)算能力，增強(qiáng)應(yīng)用意識(shí)和創(chuàng)新意識(shí)。