同步發電機定子-繞組系統耦合振動特性

摘 要：針對同步發電機定子-繞組系統耦合振動問題，重點研究了發電機定子-繞組系統的一、二次強迫耦合振動特性。首先建立了發電機鐵心和繞組系統的力學解析模型，推導得到了定子鐵心所受的磁拉力解析表達式、定子繞組所受的電磁力解析表達式，分析兩種載荷各自的激勵特性和相互間的耦合特性、定子鐵心和定子繞組的振動響應特性。然后，在有限元仿真軟件中建立了發電機三維全局模型并進行了機-電-磁多場耦合仿真計算，得到了鐵心與繞組的載荷激勵數據和力學響應數據。最后，利用YC-3型一、二次強迫振動耦合實驗機組，對繞組所受到的一次強迫振動、二次強迫振動和一、二次強迫耦合振動特性進行驗證。結果表明，發電機運行時定子-繞組系統激勵及其一、二次強迫振動均為耦合加成關系，端部繞組耦合激勵/耦合振動主要包括直流分量和二倍頻成分，且直流分量和二倍頻成分的幅值大于僅受單一激勵下的幅值。

關鍵詞：同步發電機；定子-繞組系統；定子磁拉力；繞組電磁力；耦合振動

DOI：10.15938/j.emc.2024.11.002

中圖分類號：TM311

文獻標志碼：A

文章編號：1007-449X（2024）11-0012-13

Coupling vibration characteristics of stator-winding system in synchronous generators

XU Mingxing^1，2， HE Yuling¹， ZHANG Wen¹， DAI Derui¹， FU Zixiang¹， WAN Shuting¹

（1.Hebei Engineering Research Center for Advanced Manufacturing and Intelligent Operation and Maintenance of Electric Power Machinery， North China Electric Power University， Baoding 071000，China; 2.Baoding Key Laboratory of Intelligent Measurement and Control and Industrial Interconnection， Hebei Software Institute， Baoding 071000， China）

Abstract：Regarding the issues of synchronous generator stator-winding system coupling vibration， the research focuses on the first and second forced coupling vibration characteristics of the generator stator-winding system. Firstly， the mechanical analytical model of the generator core and winding system was established， and the stator core magnetic pull force analytical expression and stator winding electromagnetic force analytical expression were derived to analyze the excitation characteristics of the two kinds of loads and their mutual coupling characteristics， as well as the vibration response characteristics of the stator core and stator winding. Then， a three-dimensional global model of the generator was established in finite element simulation software and the mechanical-electrical-magnetic multi-field coupling simulation was carried out， and the load excitation data and mechanical response data of the stator core and the winding were obtained. Finally， the first forced vibration， second forced vibration and first and second forced coupled vibration characteristics of the windings subjected to in the YC-3 type first and second forced vibration coupling experimental set were verified. It is shown that the stator-winding system excitation and its first and second forced vibrations during generator operation are both coupled and additive. The coupled excitation/coupled vibration of the end winding mainly consists of DC component and 2nd frequency component， and the amplitude of DC component and 2nd frequency component is larger than that of the single excitation only.

Keywords：synchronous generator; stator-winding system; stator magnetic pull; winding electromagnetic force; coupling vibration

0 引 言

發電機組作為電網系統的關鍵組成部分，在電網運行過程中發揮著重要作用。通常發電機組的自動保護系統根據振動幅度和繞組溫度的閾值控制來執行保護操作，且電樞繞組的劇烈振動將嚴重影響能量轉換效率并降低發電機的使用壽命，然而，發電機在實際運行過程中許多因素都將加劇繞組的振動。因此，對發電機繞組振動的監測和抑制受到越來越多的關注^[1]。

以定子端部繞組為例，由于其獨特的結構和在發電機運行過程中的重要作用，其劇烈的振動已成為發電機發生故障的主要原因之一^[2-]。到目前為止，已有許多學者對定子端部繞組的振動特性做出了出色的研究工作。例如在正常工況中，文獻[4-6]基于有限元分析計算了端部繞組的磁場分布與端部繞組電磁力的分布，并通過結合集成方法得到了轉子端部的漏磁場和繞組電磁力，最后通過實驗進行了驗證，以此來評估端部繞組的振動特性。隨后，研究人員進一步研究了發電機在偏心、短路以及偏心和短路復合故障下的端部繞組受力及振動特性^[7-8]。

由于計算機技術的快速發展，有限元軟件不斷得到改進，具備了更高的計算精度和效率。因此，在更先進的有限元軟件的輔助下，繞組電磁力在端部繞組上的詳細分布^[9]、繞組電磁力引起的端部繞組的振動響應^[10]及其特性^[11]得到了更深入的研究。更重要的是，如何在有限元軟件中建立更適合振動分析的端部繞組新模型^[12]、優化端部繞組結構設計方案^[1]以及確定端部繞組振動特性^[8，10-11]已成為新的研究課題。

現有研究已經針對端部繞組受力及振動做了大量的工作，但以往的研究工作主要集中在單一的端部繞組電磁場特性以及由其引起的繞組振動。顯然對于發電機中各部件相互聯系的復雜機械系統，其端部繞組的振動不可能僅由電磁力作用引起。Patel和Butler于二十世紀八十年代就已提出定子鐵心-繞組系統可以等同于2個自由度系統的論點^[14]。不僅繞組電磁力會引起端部繞組振動，而且鐵心振動也會通過定子繞組的直線段傳遞到端部繞組。因此，端部繞組的振動在發電機中應為耦合振動。

基于上述分析，在研究定子端部繞組的振動特性時，也應考慮定子鐵心的振動特性。對于定子鐵心的振動特性，也有很多學者進行了非常詳細的研究。例如，文獻[15]為克服解析法和有限元法在電磁力波計算中的缺點，提出一種電磁力波的快速準確計算方法。文獻[16]提出一種解析方法用于計算定子鐵心的振動特性，克服了當前有限元計算耗時太長等缺點，并驗證得到了兩者分析結果誤差小于5%。以上研究為定子振動特性的分析提供了重要參考，但未提及定子振動對端部繞組的影響。尤其是未考慮定子-繞組的激勵耦合特性與振動響應特性。

本文以定子鐵心-繞組系統的耦合振動為出發點，通過理論解析、有限元計算和動模實驗驗證探索直線段繞組二次強迫振動（定子鐵心傳遞）與端部繞組一次強迫振動（電磁力激發）的耦合作用機制，為電機設計者對耦合振動下絕緣磨損退化風險位置進行定位、針對性地進行特殊的工藝處理及相關繞組制造、安裝工藝的改進提供理論參考。

1 理論分析

1.1 物理模型

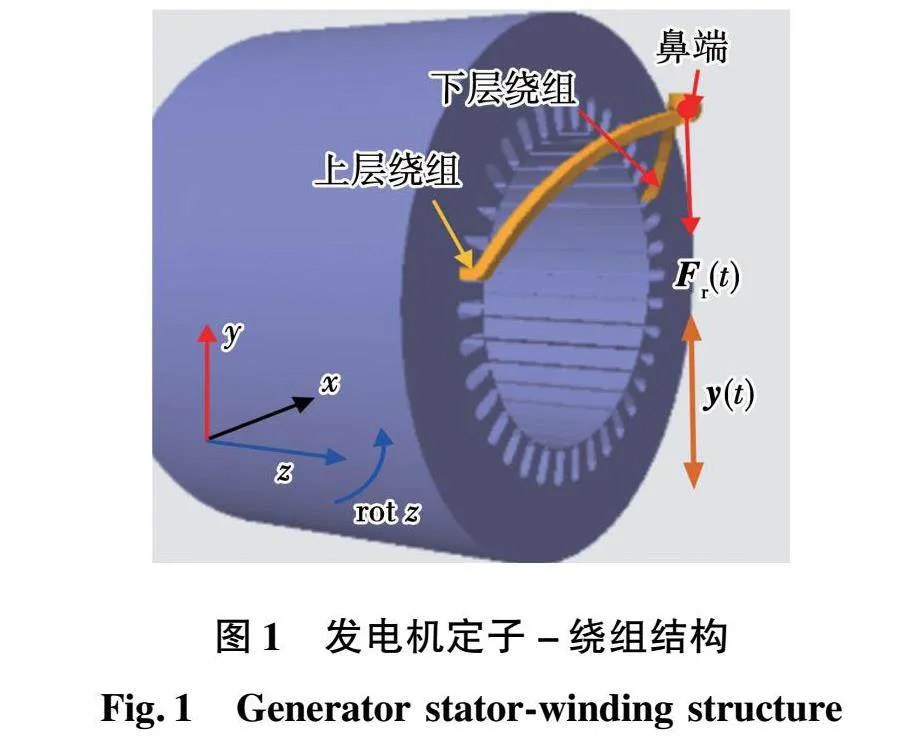
簡化后的鐵心-繞組力學激勵的耦合物理模型如圖1所示，端部繞組為類似懸臂梁結構，直線段繞組為類似多支撐彈性簡支梁結構。

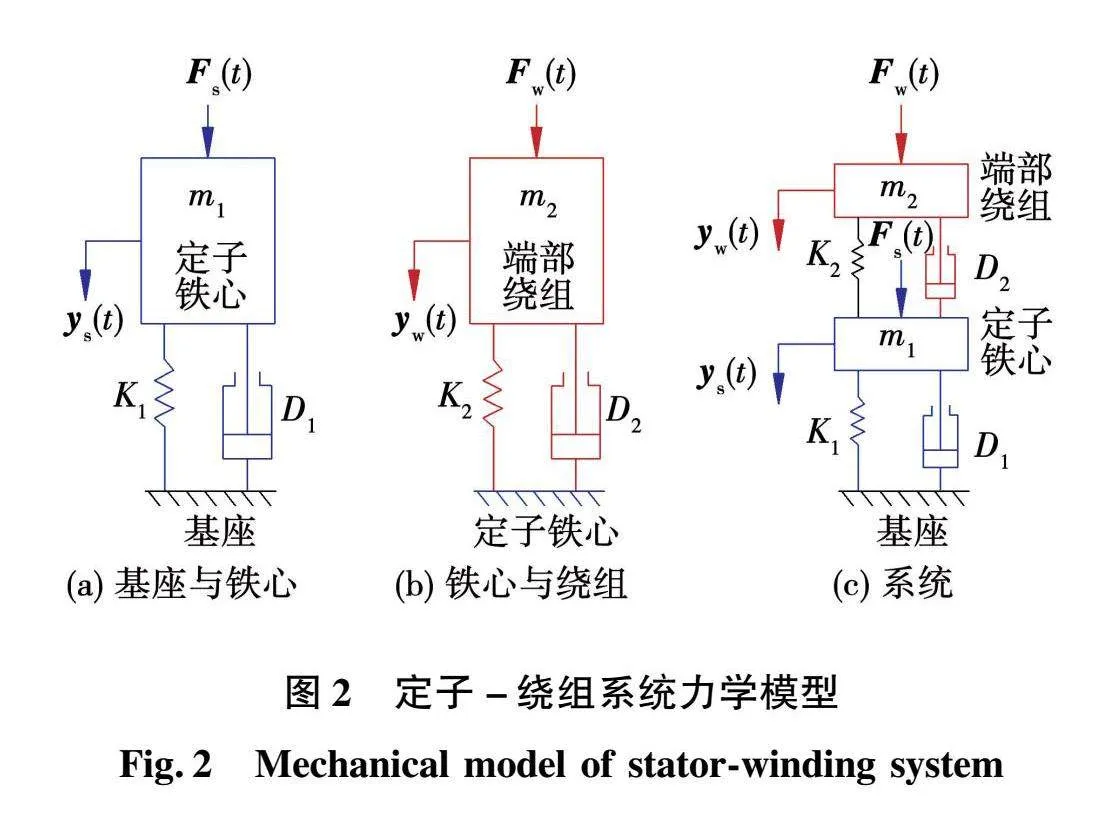
由于與端部繞組相連的直線段繞組嵌裝在鐵心中，不同運行狀態將引發定子鐵心產生不同程度、不同規律的振動，并通過直線段繞組將振動傳遞至端部繞組。相當于整個定子繞組在端部承受電磁力激勵產生振動的同時，還將承受直線段部分傳遞的來自于定子鐵心所施加的強迫振動（其本質激勵源為定子鐵心在不同運行狀態下所受的磁拉力）。因此，根據系統結構及所受約束的特點得到二力學自由度的定子-繞組精簡結構模型，如圖2所示。

圖2中：Fw為端部繞組電磁力；K1表示剛度；D1表示阻尼；yw（t）為端部繞組振動的位移矩陣，用來反映繞組總體變形量；m1表示定子鐵心質量；Fs為定子鐵心所受磁拉力；K2為剛度；D2為阻尼；ys（t）為定子鐵心振動的位移矩陣，用來反映振幅即總體變形量；m2表示繞組質量。在發電機正常運行時Fw和Fs總是同時存在，即yw（t）和ys（t）之間存在一定的耦合關系。系統的動力學方程為：

F′（t）=Ma;

F′（t）=F（t）－FK（t）－FD（t）；

F（t）=Fw（t）Fs（t）；

FK（t）=Ky（t）=k1+k2－k2－k2k2yw（t）ys（t）；

FD（t）=Dy·（t）=D1+D2－D2－D2D2y·w（t）y·s（t）；

M=m100m2；

a=y··（t）=y··w（t）y··s（t）。（1）

式中：K為剛度矩陣；D為拉線作用的阻尼矩陣；M為質量矩陣；FK（t）和FD（t）分別是由彈性彈簧和阻尼提供的抵抗力矩陣；F（t）為激勵載荷矩陣；y（t）為位移矩陣。

雖然已將實際系統化簡為多自由度系統，但研究其振動的幅值波動仍具有一定難度。因此對分析過程進行了簡化，意圖通過激勵特性來映射振動特性。即從系統的受力入手進行分析。實際上，由于技術條件的限制，這種力很難測量，因此常通過測量加速度來反應力的振動，這是因為力與繞組的加速度成比例，具體參考式（1）。

1.2 電磁力與鐵心磁拉力

對定子鐵心所受磁拉力與定子繞組所受電磁力這兩種激勵關聯耦合效應進行分析與求解。其中：定子鐵心的材料為硅鋼片，是一種典型的導磁體，定子鐵心所受的磁拉力屬于磁場力的一種（典型特征為受力體不通電）；而定子繞組材料一般為銅，是典型的導電體，他受到的電磁力（安培力）為另一種形式的磁場力（典型特征為受力體通電）。其中，氣隙磁通密度作為計算電磁力和鐵心磁拉力的關鍵參量，可由氣隙磁動勢^[17]與磁導^[18]相乘獲得。即氣隙磁通密度為

B（αm，t）=f（αm，t）Λ（αm，t）=

Fccos（ωt－pαm－β）Λ0。（2）

式中：Fc為氣隙合成磁動勢；Λ0為單位面積氣隙磁導。

由圖3可知，發電機轉子為實心圓柱體結構，而定子為對稱空心殼體結構。在正常運行時合力相互抵消，故定子振動只能用其鐵心磁拉力來反映^[19]，因此，定子振動借由內圓面所受鐵心磁拉力表達，可表示為

q（αm，t）=B（t）22μ0=［Λ0Fccos（ωt－pαm－β）］22μ0=

F2cΛ204μ0［1+cos（2ωt－2pαm－2β）］。（3）

對于定子鐵心磁拉力，可以將其理解為磁體對于導磁體的引力。再根據定子鐵心結構，可以得到定子鐵心在磁場中的受力與變形，如圖3所示。

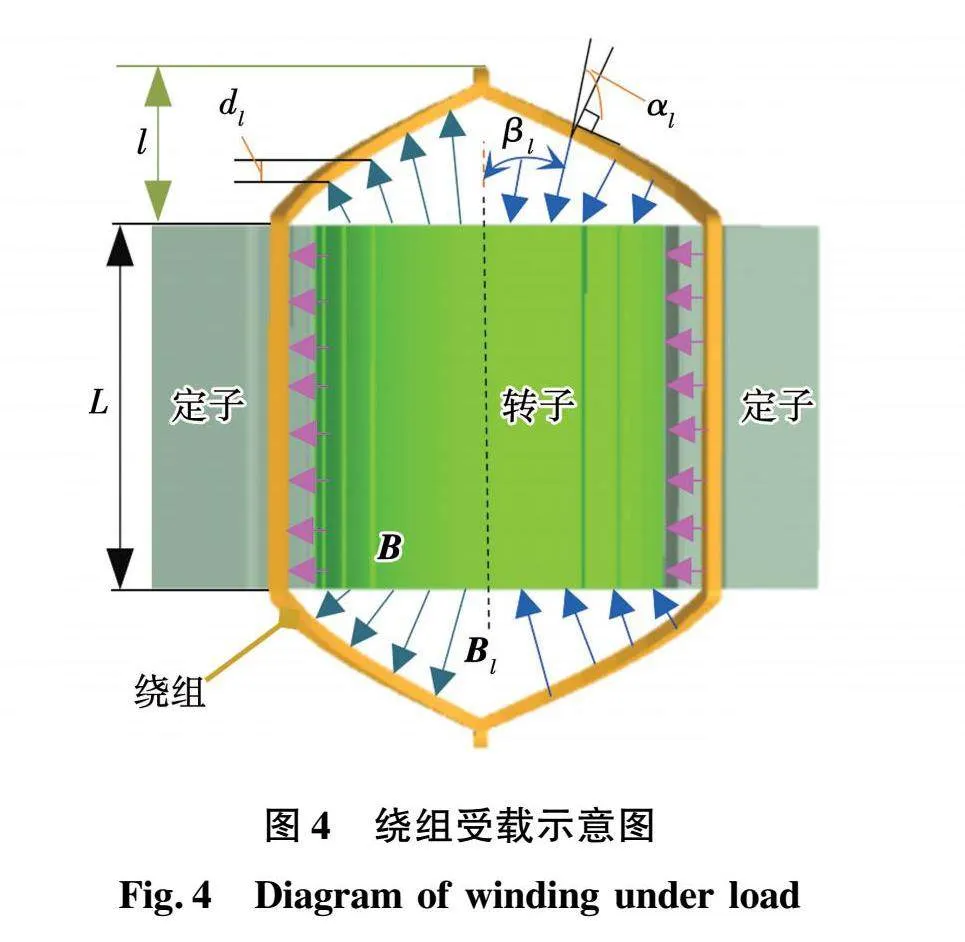
根據圖1與圖4所示的繞組結構及其受載示意圖，端部繞組電磁力^[20]為

Fs（αm，t）=∫l0Bl（αm，t）i（αm，t）cosαlsinβldl=

∫l0Bl（αm，t）［B（αm，t）Lv/Z］cosαlsinβldl=

ηB2（αm，t）Llv/Z=

12F2cΛ20ηLlv［cos（2ωt－2pαm－2β）+1］/Z。（4）

式中：Bl（αm，t）為發電機端部磁通密度，數值上為B（αm，t）與削弱系數η的乘積，其中0lt;ηlt;1；i為電流；L為繞組直線部分的長度；l為繞組漸開線部分軸向長度；αl為端部繞組某點磁通密度與該點法線的夾角；βl為端部繞組某點法線與轉子軸線的夾角；v為直線段繞組切割磁感線的速度；Z為阻抗。

發電機在無故障時磁場呈對稱分布，如圖5所示。在1個周期內發電機內部磁場變化可以分解為4種特殊時刻的狀態，如圖6所示。

由圖6可得，1對極同步發電機直線段繞組電磁力方向總是在切向和徑向之間來回切換。具體來說，發電機從狀態1變為狀態3時，轉子旋轉了180°，同時繞組電流方向也發生了改變。根據左手定則可得出直線段繞組電磁力方向為切向，如圖6（a）和圖6（c）所示；同理，發電機從狀態2變為狀態4時，直線段繞組電磁力方向為徑向（垂直于圓心向外）。根據電磁力方向的變換次數，可直觀地得出繞組電磁力的頻率為發電機工頻（50 Hz）的兩倍（100 Hz）。

1.3 耦合特性

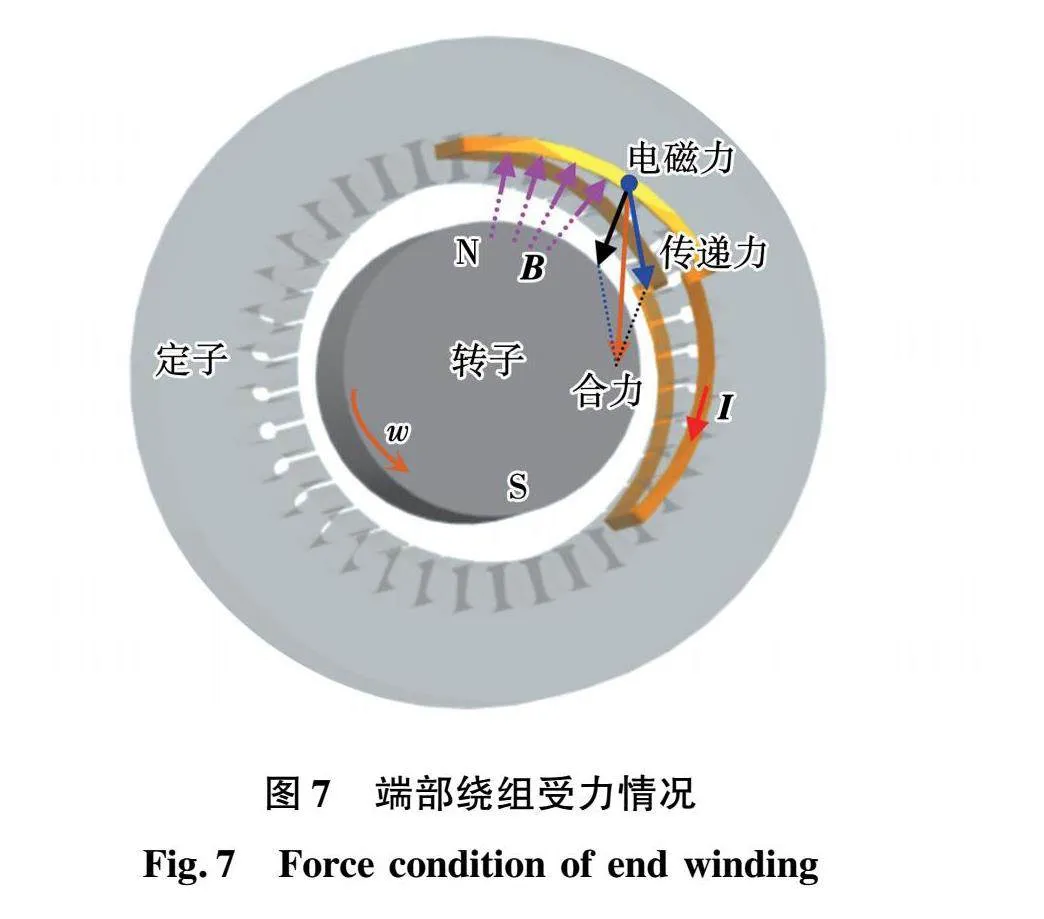
所研究的發電機以系統工頻旋轉。由式（3）和式（4）可知，忽略高次諧波后，電磁力和磁拉力存在同頻成分（直流分量和二倍頻成分）。鐵心磁拉力與繞組電磁力為同頻關系，將其看作2個同頻的周期信號。但因為磁拉力與電磁力作用對象不同，不能直接耦合，在實際的發電機中，定子鐵心將受到磁拉力而產生振動，振動將通過繞組直線段傳遞到端部，而端部也會受到電磁力的作用而產生與傳遞的振動同頻的振動，故實際發電機繞組與鐵心的關系為振動（位移）耦合。為簡化計算，將定子鐵心傳遞至端部繞組的振動簡化為一個力作用在端部繞組上而產生的振動，此力為傳遞力q1，如圖7所示。故繞組的振動可看作傳遞力與電磁力耦合作用后的結果。另外，近似認為傳遞力與定子鐵心磁拉力一致。

首先，通過對傳遞力與繞組電磁力的互相關分析獲取兩種激勵的相位差確定兩者的關系。設兩信號分別為x（t）和y（t），且其表達式為：

x（t）=A1sin（ωt+θ）;y（t）=A2sin（ωt+θ+φ）。（5）

由于x（t）、y（t）具有相同的周期，故兩者符合同頻相關，其互相關函數為

Rxy（τ）=limT→∞1T∫T0x（t）y（t+τ）dt=

1T0∫^T00A1sin（ωt+θ）A2sin［ω（t+τ）+θ+φ］dt=12A1A2cos（ωτ+φ）。（6）

式中T0為兩列信號的周期。

在互相關函數Rxy（τ）中，不僅保留了相位差φ的信息，而且完整保留了兩信號的ω及A的信息。利用該方法，將式（6）中的x（t）和y（t）用端部繞組電磁力和傳遞力代入發現兩者時間上的相位差為0。

根據力的合成原理，得到發電機繞組受載情況示意圖，如圖7所示。進而得到繞組的合力表達式為

|F|=|q1+Fs|=

|q1|2+|Fs|2－2|q1‖Fs|cos（π－φ）=

Z2+4η2L2l2v2μ20+4ηLlvμ0Zcosφ=

F2cΛ20［1+cos（2ωt－2pαm－2β）］4μ0Z×

Z2+4η2L2l2v2μ20+4ηLlvμ0Zcosφ。（7）

其中：

|q1|=F2cΛ204μ0［1+cos（2ωt－2pαm－2β）］；

|Fs|=ηF2cΛ20Llv2Z［1+cos（2ωt－2pαm－2β）］。（8）

式中φ為傳遞力與繞組端部電磁力夾角。

由圖8可得，傳遞力與繞組端部電磁力夾角φ與發電機繞組節距有關，由發電機結構可得

φ≤y2360°z≤τ2360°z=z2p2360°z=90°p。（9）

式中：p為極對數；z為定子槽數；τ為極距，2個磁極之間的距離，通常采用定子槽數來表示；y為繞組節距，繞組線圈兩條直線邊間隔的距離，可用定子槽數來表示。

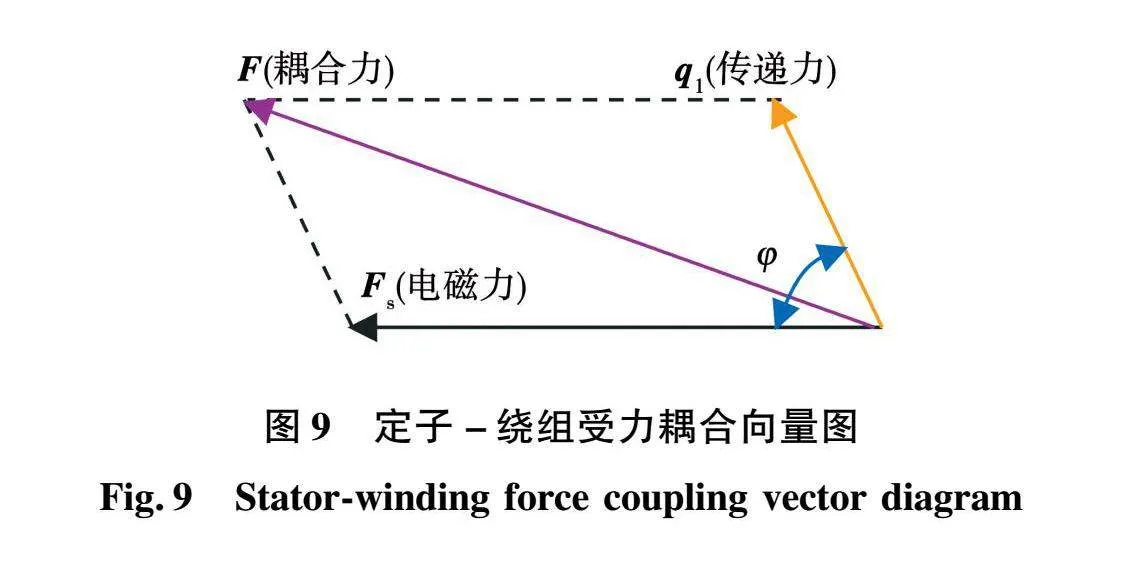
所以當發電機確定后，傳遞力與繞組端部電磁力夾角也就隨之確定了，且其一般小于90°。傳遞力與繞組端部電磁力矢量圖如圖9所示，結合時域相位差與分析的空間關系可以推斷出系統的激勵為加成耦合關系，故振動也應為加成關系。

2 有限元仿真

2.1 研究對象及設置

根據河北省電力機械裝備健康維護與失效預防重點實驗室的CS-5型故障模擬發電機參數進行了三維有限元建模，如圖10（a）所示。為了與實驗機組保持一致，有限元仿真通過設置外接電路使發電機在額定工況下運行，如圖10（b）所示。發電機的關鍵參數如表1所示。

經過有限元仿真分析后，將得到的計算結果導入另一個模塊中，計算繞組機械響應，數據導入過程如圖10（c）所示。

2.2 仿真分析

從圖11中可以看出，當轉子逆時針旋轉180°從圖11（a）狀態1變為圖11（c）狀態3時，直線段繞組電磁力與端部繞組電磁力大小和方向均未發生巨大改變。另外，直線段繞組電磁力方向雖然未能嚴格指向轉子切向方向，但大部分電磁力方向仍保持一致，始終朝向轉子轉動方向。端部繞組電磁力方向與直線段繞組電磁力方向相比有些許變化，其與繞組切線垂直且遠離發電機端部，并與端部呈銳角。此外，從圖11（b）狀態2變為圖11（d）狀態4時，轉子依然轉動了180°，并且從圖中可以看出直線段繞組電磁力的方向始終沿徑向方向（垂直于圓心向外），端部繞組電磁力與繞組切線垂直且指向遠離軸線方向。

從圖11中可以發現，從狀態1到狀態4實際上就是發電機轉子的一個旋轉周期。在這個旋轉周期內，繞組電磁力的方向跟隨轉子的轉動變化了2次，由此可得繞組電磁力的頻率為100 Hz。圖11與圖6基本保持一致，說明對定子繞組電磁力的仿真較好地驗證了理論推導的準確性。

同樣在圖12中，定子鐵心所受磁拉力隨著轉子磁極轉動而發生變化，在狀態1和狀態3中，定子鐵心各部位所受磁拉力大小幾乎一致，方向皆沿徑向并指向圓心；同理，狀態2和狀態4亦是如此。從狀態1到狀態4定子鐵心磁拉力在發電機的一個轉動周期內變換了2次。可以得出定子鐵心磁拉力與繞組電磁力頻率一致，即都為100 Hz。顯然，圖12所得結果與圖3理論分析結果一致。

為了更加直觀地表示繞組變化趨勢，利用仿真軟件中的“probe”探針工具，并在繞組中選擇了5個測點對繞組變形量進行分析。具體位置如圖10（d）所示，其中，測點1和測點5位于直線部分與漸開線部分的連接處，測點2和測點4位于漸開線部分的中間位置，測點3位于繞組鼻端。不同激勵導致的繞組變形量如圖13、圖14和圖15所示。將圖13、圖14和圖15中的變形值進行總結整理，如圖16所示。圖16中圖例“電磁力”為定子繞組電磁力導致的變形量幅值，簡稱一次強迫振動。“磁拉力”為定子鐵心磁拉力導致的定子端部繞組變形量幅值，簡稱二次強迫振動。“耦合”則是定子繞組電磁力和定子鐵心磁拉力同時施加，即傳遞力與電磁力耦合激勵下的繞組變形量幅值，簡稱一、二次強迫耦合振動。

從圖16中可以看出無論在何種狀態下，“耦合”激勵下的形變量幅值總是最大。且在4種狀態下，“耦合”作用下5個測點的變形量也為最大值。仿真分析結果可以得出一次強迫振動與二次強迫振動為耦合加成關系，與理論結果基本一致。

3 樣機試驗

3.1 實驗設置

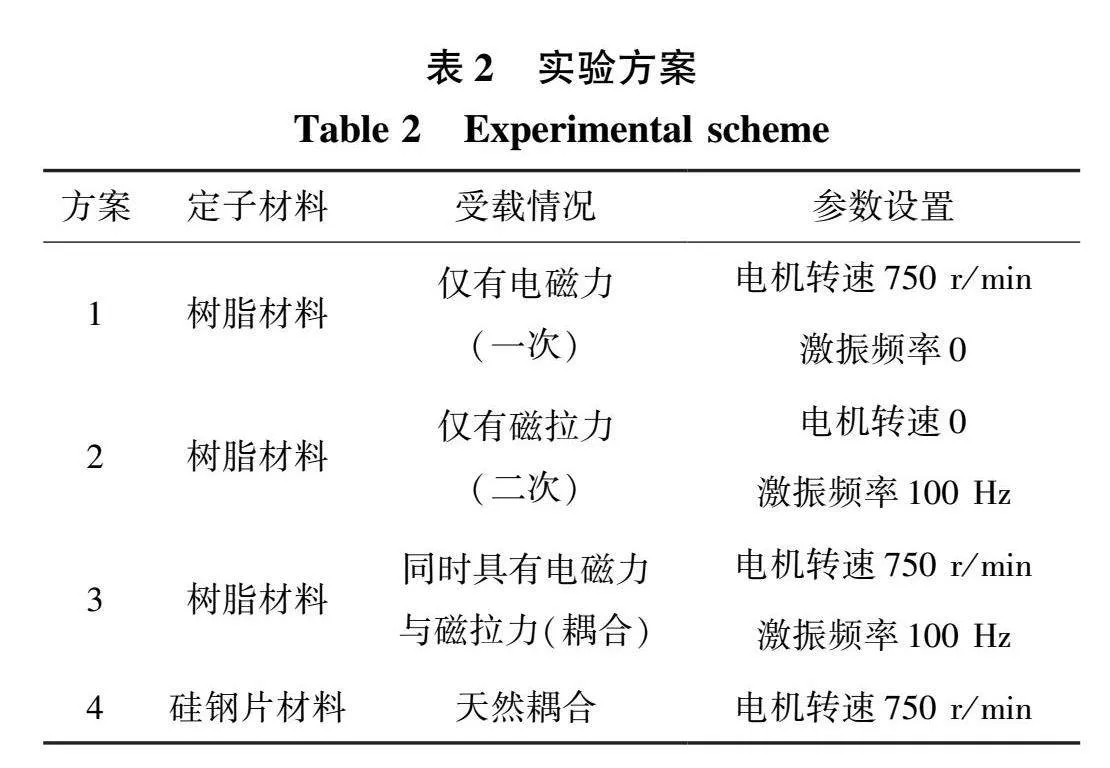
為實現對一次強迫振動和二次強迫振動的單獨模擬，作者設計并制作了YC-3型一、二次強迫振動耦合實驗機組。該機組能夠將繞組電磁力和定子鐵心磁拉力進行分離。由于端部繞組的受力情況復雜、模擬難度大，而定子鐵心上某處的振動變化近似于正弦，模擬定子鐵心磁拉力將更為容易，所以從定子鐵心所受磁拉力沿徑向的特點入手設計實驗方案。設計了一個樹脂材料“鐵心”（近似空氣磁路），利用激振器徑向激振“鐵心”來模擬定子鐵心磁拉力，如圖17（a）所示。

在實驗中設置四對極發電機的轉速為750 r/min，系統工頻為50 Hz。發電機繞組作為一個閉合回路，在旋轉磁場中作切割磁感線運動，繞組回路中產生感應電動勢，從而在繞組中產生電流。最后通電導體在旋轉磁場中產生力的作用，即繞組電磁力。

具體實驗驗證方法為：

1）機組運行，激振器不工作，獲取繞組在電磁力激勵下的振動響應。由于定子鐵心為樹脂材料不導磁，不會因鐵心受磁拉力而引發電磁振動，此時測得的繞組振動即為電磁力所激發的振動，見圖17（b）。

2）機組不運行，將不同方案下的定子磁拉力波形作為輸入，使激振器對樹脂材料定子鐵心進行激勵，獲得繞組二次強迫振動響應，見圖17（c）。

3）機組運行，激振器也運行（樹脂定子），見圖17（f），此時測得的繞組振動即為一、二次強迫耦合振動。

4）機組運行，激振器不運行（硅鋼片定子），見圖17（e），此時測得的繞組振動即為天然耦合振動（一、二次強迫耦合振動），見圖17（d）。

5）對比前面4種情況下測得的振動響應，驗證其是否符合合成規律，具體實驗方案見表2。

在實驗過程中激振器頻率設置為系統工頻的2倍，100 Hz，即可模擬由磁拉力引起的定子鐵心振動，并將振動傳遞到繞組。YC-3型機組實驗中發電機繞組的振動數據由壓電陶瓷雙屈曲梁（piezoelectric ceramic bimorph，PCB）加速度傳感器測取，且傳感器布置位置與有限元仿真中測點3（見圖10（d））位置相同，都位于端部繞組鼻端。

3.2 實驗分析

通過表2中實驗方案4得到的硅鋼片材料定子（常規發電機）的端部繞組振動加速度如圖18所示。通過調節激振力的大小，直至方案3中的端部繞組振動加速度具體數值與方案4相同，如圖19（c）和圖19（f）所示（實驗數據提取轉換幅值存在微小差異，可忽略不計），此時激振力的大小為5 N。類似的在方案2中設置激振力大小為5 N，以模擬作用在定子繞組上的傳遞力（忽略定子為樹脂材料自身物理、機械性能在二次強迫振動和一、二強迫耦合振動的影響）。

如圖19所示，端部繞組振動的主要頻率成分為二倍頻，與仿真和理論得到的特征頻率成分一致；此外，由圖19可知一、二次強迫耦合振動在徑向方向的幅值總是大于單獨的強迫振動。實驗結果證明了系統的一、二次強迫振動為加成耦合關系。

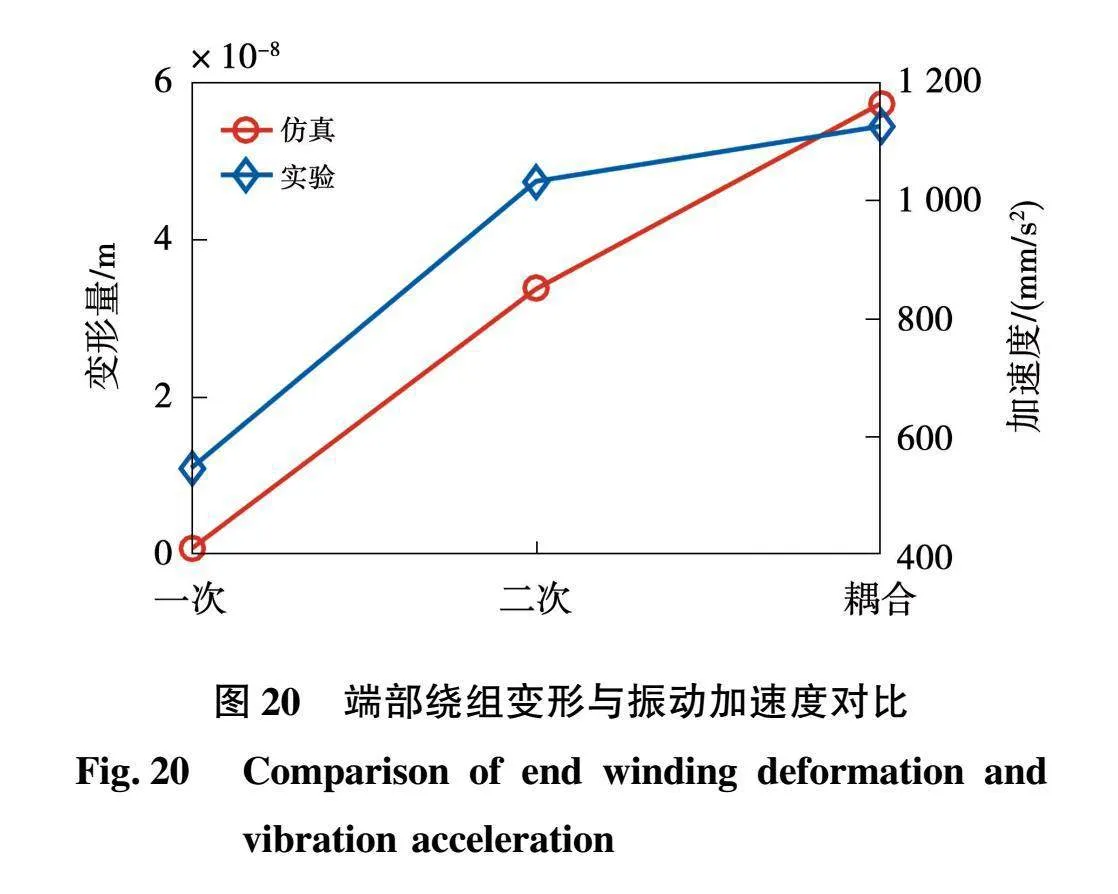
取狀態1中的端部繞組測點3在不同激勵下的變形幅值與測試的振動進行對比，如圖20所示，可以發現在耦合情況下端部繞組的變形量和加速度為最大。與理論推導結果基本一致。

4 結 論

本文通過理論推導、有限元仿真計算和實驗驗證對同步發電機額定運行工況下定子-繞組系統的一、二次強迫耦合振動特性進行了分析，結論如下：

1）定子-繞組系統的一次強迫振動的激勵源為繞組電磁力，二次強迫振動的激勵源為定子鐵心磁拉力，其二者的主要頻率成分均為二倍頻。

2）發電機運行時，直線段繞組電磁力方向總是在徑向和切向間來回切換。

3）定子-繞組系統合力振動的耦合關系為加成關系。合力振動主要包含直流分量和二倍頻成分，且頻率成分幅值都大于僅受單一激勵下的幅值。

4）無論轉子在何種狀態，5個測點變形量在耦合激勵情況下總是最大。

本研究將有助于更全面地了解發電機的性能和振動特性，尤其是定子鐵心磁拉力與電樞繞組電磁力之間的相互作用。研究內容能夠給發電機繞組振動磨損和絕緣保護提供寶貴的參考依據。

下一步工作將進一步分析繞組在電磁力激勵下振動響應導致的絕緣磨損規律，找出絕緣破壞的危險位置點，以期在制造裝配過程中有針對性地對危險位置進行特殊工藝處理，實現絕緣磨損的主動預防。

參 考 文 獻：

［1］ 肖陽，宋金元，屈仁浩，等.變頻諧波對電機振動噪聲特性的影響規律[J]. 電工技術學報，2021，36（12）： 2607.

XIAO Yang， SONG Jinyuan， QU Renhao， et al. The effect of harmonics on electromagnetic vibration and noise characteristic in inverter-duty motor[J]. Transactions of China Electrotechnical Society， 2021， 36（12）： 2607.

［2］ LETAL J， SATMOKO B， MANIK N. Statorend-winding vibration in two-pole machines： avoiding generator failure [J]. IEEE Industry Applications Magazine， 2020， 26（6）： 29.

［3］ KREISCHER C. Modern methods to monitor end winding vibrations in turbo-generators [J]. COMPEL-The International Journal for Computation and Mathematics in Electrical and Electronic Engineering， 2019， 38（4）：1214.

［4］ 趙洋，劉晉琿，肖洋，等. 大型汽輪發電機定子端部繞組物理參數識別及數學模型建立方法研究 [J]. 振動與沖擊， 2024， 43 （5）： 202.

ZHAO Yang， LIU Jinhui， XIAO Yang， et al. Identification of physical parameters and establishment of mathematical model for stator end winding of large turbogenerator[J]. Journal of Vibration and Shock， 2024， 43（5）：202.

［5］ 王頲，楊震，趙洋，等. 大型發電機端部繞組電磁力物理數字孿生建模[J].計算機集成制造系統，2024，30（9）：2998.

WANG Tian， YANG Zhen， ZHAO Yang， et al. Digital twin modelling of electromagnetic-force physics for large turbo-generator stator-end winding [J]. Computer Integrated Manufacturing Systems， 2024， 30（9）：2998.

［6］ 趙洋，何樂，劉晉琿，等. 基于近似模型的大型汽輪發電機定子端部繞組動力響應預測研究 [J]. 振動與沖擊， 2023， 42（21）： 81.

ZHAO Yang， HE Le， LIU Jinhui， et al. Dynamic response predietion of large turbo-generator stator end winding based on approximate model[J].Journal of Vibration and Shock， 2023，" 42（21）： 81.

［7］ 何玉靈，徐明星，張文，等. 氣隙靜偏心故障對永磁風力發電機定子繞組振動的影響 [J]. 中國工程機械學報， 2024， 22 （1）： 83.

HE Yuling， XU Mingxing， ZHANG Wen， et al. Impact of static air gap eccentricity fault on stator winding vibration in permanent magnet wind generator [J]. Chinese Journal of Construction Machinery， 2024， 22（1）： 83.

［8］ XU Mingxing， HE Yuling， ZHANG Wen， et al. Comprehensive investigation of winding mechanical properties in generators under RISC： Impact of position， degree， and eccentricity [J]. IEEJ Transactions on Electrical and Electronic Engineering， 2024， 19（11）：1842.

［9］ 喬長帥，唐贏武，鐘博.牽引電機定子端部繞組電磁力計算分析[J].電機技術，2020（5）：15.

QIAO Changshuai， TANG Yingwu， ZHONG Bo. Calculation and analysis of electromagnetic force in stator end winding of traction motor[J]. Electrical Machinery Technology， 2020（5）： 15.

［10］ HE Yuling， XU Mingxing， ZHANG Wen， et al. Impact of stator interturn short circuit position on end winding vibration in synchronous generators[J]. IEEE Transactions on Energy Conversion， 2021， 36（2）： 713.

［11］ DAI Derui， HE Yuling， XU Mingxing， et al. Mechanical properties and insulation damage of PMSG stator end windings with eccentricity considerations[J]. Alexandria Engineering Journal， 2024， 105：156.

［12］ IGA Y， TAKAHASHI K， YAMAMOTO Y. Finite element modelling of turbine generator stator end windings for vibration analysis[J]. IET Electric Power Applications， 2016， 10（2）：75.

［13］ ZHAO Y， YAN B， ZENG C， et al. Optimal scheme for structural design of large turbogenerator stator end winding[J]. IEEE Transactions on Energy Conversion， 2016， 31（4）：1423.

［14］ PATEL M R， BUTLER J M. End-winding vibrations in large synchronous generators[J]. IEEE Transactions on Power Apparatus and Systems， 1983， 102（5）：1371.

［15］ 邢澤智，王秀和，趙文良，等.表貼式永磁同步電機電磁激振力波計算與定子振動特性分析[J].中國電機工程學報， 2021， 41（14）： 5004.

XING Zezhi， WANG Xiuhe， ZHAO Wenliang， et al. Calculation of electromagnetic force waves and analysis of stator vibration characteristics of surface mount permanent magnet synchronous motor [J]. Proceedings of the CSEE， 2021， 41（14）： 5004.

［16］ 屈仁浩，蔣偉康.電機定子鐵心振動特性分析的一種解析方法[J].振動與沖擊， 2021， 40（3）： 81.

QU Renhao，JIANG Weikang. An analytical method for vibration characteristics analysis of motor stator core [J]. Journal of Vibration and Shock， 2021， 40（3）： 81.

［17］ HE Yuling， JIANG Mengya， SUN Kai， et al. Comprehensive analysis on rotor vibration characteristics based on a novel dynamic stator interturn short circuit model of synchronous generator [J]. IEEE Transactions on Energy Conversion， 2024， 39（3）： 1658.

［18］ 何玉靈，雷歡，張文，等. 三維氣隙偏心對同步發電機轉子鐵心溫度特性的影響 [J].電力自動化設備， 2021， 41（7）： 196.

HE Yuling，LEI Huan，ZHANG Wen，et al. Impact of three-dimensional air gap eccentricity on rotor core temperature of synchronous generator [J]. Electric Power Automation Equipment， 2021， 41（7）： 196.

［19］ 何玉靈，孫凱，孫悅欣，等. 氣隙軸向靜偏心對發電機定子-繞組受載及振動的影響[J].振動工程學報， 2022， 35（3）： 745.

HE Yuling， SUN Kai， SUN Yuexin， et al. Impact of axially static air-gap eccentricity on load and vibration of stator-winding system in generator [J]. Journal of Vibration Engineering， 2022， 35（3）： 745.

［20］ 何玉靈，張文，張鈺陽，等. 發電機定子匝間短路對繞組電磁力的影響[J].電工技術學報，2020，35（13）： 2879.

HE Yuling， ZHANG Wen， ZHANG Yuyang， et al. Effect of stator inter-turn short circuit on winding electromagnetic forces in generators[J]. Transactions of China Electrotechnical Society， 2020， 35（13）： 2879.

（編輯：劉琳琳）