借助函數對稱性，巧解數學綜合題

■孫艷艷

函數的對稱性是函數基本性質中最為特殊的一個性質,在歷年高考命題中,函數的對稱性常與函數的其他性質綜合交匯,成為數學分析、數學應用與數學研究的一大有力工具。

一、函數對稱性的一些重要“二級結論”

性質1:函數y=f(x+a)是偶函數?函數y=f(x)的圖像關于直線x=a對稱?等式f(a+x)=f(a-x)成立。

性質2:函數y=f(x+a)是奇函數?函數y=f(x)的圖像關于點(a,0)中心對稱?等式f(a+x)=-f(a-x)成立。

推論1:等式f(x)+f(2a-x)=0成立?函數y=f(x)的圖像關于點(a,0)中心對稱?函數y=f(x+a)是奇函數。

推論2:函數y=f(x+a)-b是奇函數?函數y=f(x)的圖像關于點(a,b)中心對稱?等式f(a+x)+f(a-x)=2b成立。

性質3:函數y=f(a+x)與y=f(ax)的圖像關于y軸對稱,函數y=f(a+x)與y=-f(a-x)的圖像關于坐標原點對稱。

二、函數對稱性的綜合應用

1.函數值的求解

例1 設函數f(x)的定義域為R,f(x+1)為奇函數,f(x+2)為偶函數,當x∈[1,2]時,f(x)=ax2+b。若f(0)+f(3)=3,則的值是( )。

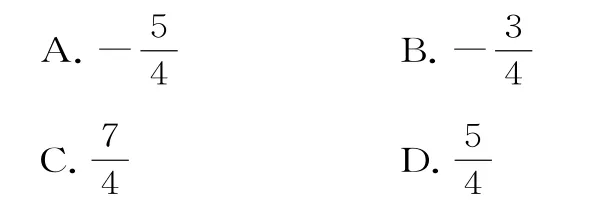
分析:結合抽象函數的奇偶性和函數對稱性的性質,構建函數關系式,確定函數的周期,利用賦值求出函數的解析式,即得函數的值。

解:由f(x+1)為奇函數,結合性質2得函數f(x)的圖像關于點(1,0)對稱,則f(1)=0,且f(x+1)=-f(-x+1)。 ①

由f(x+2)為偶函數,結合性質1 得函數f(x)的圖像關于直線x=2 對稱,則f(x+2)=f(-x+2)。 ②

熟練掌握一些函數對稱性及其對應的關系式,可以較快構建一些合適的關系式,為問題的有效解決奠定基礎。

2.代數式的求解

例2 已知函數f(x)=(2x2-4x+3)·(ex-1-e1-x)-2x+1在區間[0,2]上的最大值為M,最小值為m,則M+m=。

分析:構造函數g(x),結合關系式的結構特征,得到g(x)+g(2-x)=0,確定函數g(x)的中心對稱,利用對稱性的基本性質即可求值。

由函數對稱性的基本性質,可知M+m=-1×2=-2。

抓住函數關系式的變形與應用,構建不同函數關系式之間的聯系,為進一步利用函數的對稱性質提供條件。

3.不等式的求解

例3 已知f(x-1)是定義在R 上的奇函數,f(1)=0,且f(x)在[-1,0)上單調遞增,在[0,+ ∞)上單調遞減,則不等式f(2x-3)<0的解集為( )。

A.(1,2)

B.(-∞,1)

C.(2,+∞)

D.(-∞,1)∪(2,+∞)

分析:利用函數的對稱性與單調性,確定函數的單調區間,通過自變量取值的分類討論,得到不等式的解集。

解:由f(x-1)是定義在R 上的奇函數,結合性質2得f(x-1)=-f(-x-1),即函數f(x)的圖像關于點(-1,0)對稱。

當x=-2 時,代入上式得f(-3)=-f(1)=0,當x=0時,代入上式得f(-1)=-f(-1),即f(-1)=0。由f(x)在[-1,0)上單調遞增,在[0,+∞)上單調遞減,利用奇函數f(x)關于(-1,0)對稱知f(x)在(-∞,-2)上單調遞減,在(-2,0)上單調遞增,在(0,+∞)上單調遞減。

對于不等式f(2x-3)<0,當2x-3<-2時,2x-3>-3,解得x<0;當-2≤2x-3≤0時,2x-3<-1,解得0≤x<1;當2x-3>0時,2x-3>1,解得x>2。

綜上可得,不等式f(2x-3)<0 的解集為(-∞,1)∪(2,+∞)。應選D。

解題時,注意分類討論的巧妙應用,以及函數單調性的逆向應用。

4.綜合應用問題

例4 已知函數f(x)的定義域為R,且f(x+2)為偶函數,f(2x+1)為奇函數,則下列選項中的值一定為0的是( )。

C.f(2) D.f(4)

分析:結合題設條件,確定函數的周期性,利用奇函數的性質確定對應的特殊值,為問題的判斷提供有力根據。

解:由函數f(x+2)為偶函數,結合性質1得f(2+x)=f(2-x),則f(x+3)=f(1-x)。由函數f(2x+1)為奇函數,結合性質2 得f(1-2x)=-f(2x+1),所 以f(1-x)=-f(x+1),所以f(x+3)=-f(x+1),則f(x+1)=-f(x-1),所以f(x+3)=f(x-1),即f(x)=f(x+4),故函數f(x)是以4為周期的周期函數。因為f(2x+1)為奇函數,所以f(1)=0,所以f(-1)=f(-1+4)=f(3)=f(2+1)=-f(1)=0,B 正確。由f(2+x)=f(2-x),令x=2,可得f(4)=f(0),f(0)的值無法確定,D 錯誤。由f(x+2)=-f(x),f(0)的值無法確定,可知f(2)的值無法確定,C錯誤。同理,的值也無法確定,A 錯誤。應選B。

這里綜合函數的奇偶性、對稱性與周期性,結合幾個不同函數值的設置,巧妙得到函數值為0 的一個選項。