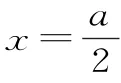例說二次函數y=ax2+bx+c(a≠0)在閉區間[m,n]上的最值問題
2024-01-27 07:06:18王岳軍
中學生數理化·高一版 2024年1期
■王岳軍
閉區間上二次函數的最值問題,從數的角度而言,與二次項系數a的正負有關,與的值有關,與的值和m,n的大小關系有關;從形的角度而言,與二次函數的圖像的開口方向有關,與圖像的對稱軸有關,與對稱軸和閉區間的位置關系有關。
例1 若函數f(x)=2x2-2ax+3 在[-1,1]上有最小值,記作g(a),求g(a)的表達式。
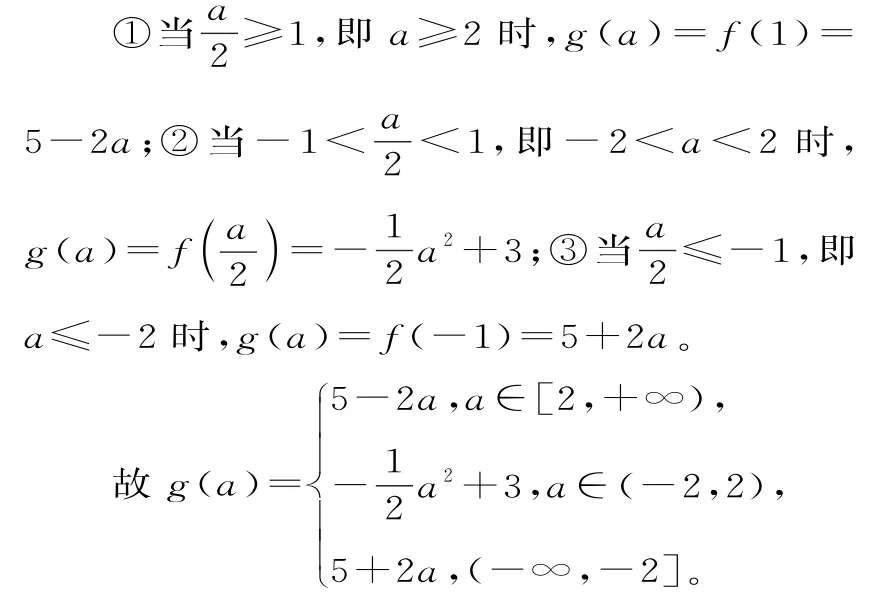
解:此函數的圖像開口向下,對稱軸為x=0,下面分三種情況討論求解。

當a+b=0 時,f(a)=f(b),2a=f(a)=f(b)=2b,此時a的值不存在;
當a+b<0時,f(a) 綜上可得,區間[a,b]為[1,3]或 例3 若函數y=log0.5(x2-ax+3a)在區間[2,+∞)上是減函數,求實數a的取值范圍。 解:要使此函數在區間[2,+∞)上有意義,需滿足f(x)=x2-ax+3a在區間[2,+∞)上的最小值大于零。由f(x)的最小值f(2)=4-2a+3a=4+a>0,解得a>-4。 結合復合函數的單調性知f(x)=x2-ax+3a在區間[2,+∞)上為增函數,且區間[2,+∞)必在此拋物線的對稱軸的右側,即,解得a≤4。 故實數a的取值范圍為-4