GeoGebra支持下POE教學策略實踐研究

寧鎮宇　夏羿娥　馮潔　李紅梅

［摘 要］利用POE教學策略結合GeoGebra軟件設計“拋體運動的規律”的教學方案，可以體現以學生為主體、教師為主導的教學觀。運用GeoGebra軟件，可以將拋體運動規律更加直觀地顯示出來，這樣有利于學生觀察與研究，有利于培養學生動手操作和解決問題的能力。

［關鍵詞］POE教學策略；拋體運動規律；GeoGebra

［中圖分類號］? ? G633.7? ? ? ? ［文獻標識碼］? ? A? ? ? ? ［文章編號］? ? 1674-6058（2023）29-0054-04

POE（Predict-Observe-Explain，意為預測、觀察、解釋）教學策略是基于學生行為建立的實驗演示策略［1］。在這種策略的指引下，教師以學生為主體開展演示活動。運用GeoGebra軟件的目的是將抽象的現象變得更加直觀，有利于學生觀察。本文將POE教學策略和GeoGebra軟件有機融合，用于探究拋體運動的規律，以幫助學生加深對平拋運動規律的理解，幫助學生建構物理知識，培養學生發現問題和解決問題的能力。

一、POE教學策略的理論研究

（一）理論基礎

建構主義理論認為，知識的學習是個體積極主動地進行意義建構的過程，學生在經歷圖式、順應、同化、平衡后，將他們在日常生活和學習中積累的經驗、看法、見解整合成新的知識進行建構，進而形成新的見解和經驗［2］。POE教學策略的預測、觀察、解釋的三個階段剛好和建構主義的四個過程高度一致。可見，建構主義學習理論為POE教學策略提供了理論基礎。

（二）POE教學策略的來源

POE教學策略是由岡斯通（Gunstone）和懷特（White）于1992年提出的。它分為三個環節：預測、觀察、解釋，是一種應用于實驗的演示策略［3］。它與傳統的演示實驗過程相比，更能體現以學生為主體、以教師為主導的實驗過程，并且運用POE策略能暴露學生已有的前概念。學生暴露前概念后，教師可以根據學生暴露的問題進行教學設計，從而在教學過程中將學生的前概念進行轉變，加深學生對新概念的理解。POE教學策略下的演示實驗可以引起學生的好奇心，激發學生的學習興趣，這對提高教學效率有一定的幫助。

在傳統的演示實驗過程（提出問題—猜想與假設—制訂計劃與設計實驗—進行實驗與收集證據—分析與論證—評估—交流與合作）中，教師占據主體地位（實驗操作過程和演示都是教師一個人完成），而學生的任務是觀察與記錄，這違背了當前的教育教學觀，不利于培養學生的動手操作能力以及發現問題與解決問題的能力。而POE教學策略符合當前素質教育的教學觀。

（三） POE教學策略的三個環節

預測（P）：是指學生結合自己已有的生活經驗和在教師設定的特定情境（提供的素材、視頻、實驗作為預測提示）下做出的預判。

觀察（O）：指學生在教師的指導下進行實驗、觀察現象，得出總結。

解釋（P）：指教師引導學生運用所學知識解釋觀察結果和預測結果之間的相同之處和差異。

它們三者之間的關系：預測是實施POE教學策略的開始環節，是觀察和解釋的前提，起到先鋒的作用；觀察是實施POE教學策略的中間環節，對預測和解釋有承上啟下的作用；解釋是實施POE教學策略的最后環節，是對預測和觀察的總結。

（四） POE教學策略的流程圖

POE教學策略的三個環節環環相扣，每個環節都有不同的步驟，利用流程圖的模式將POE教學策略整合成如圖1所示的關系圖。

二、GeoGebra軟件的介紹

GeoGebra是一套結合幾何、代數、數據表、圖形、統計和計算的動態數學軟件，同時具有處理代數與幾何的功能，其功能強大，操作簡單［4］。將GeoGebra軟件應用于“拋體運動的規律”教學，可以將平拋運動直觀化，激發學生的學習興趣，促進學生物理觀念、科學思維的形成。

三、教學設計

（一）教材分析

“拋體運動的規律”是新人教版高中物理必修第二冊第五章“拋體運動”中的第4節，具體可以把拋體運動的知識點分為三個階段進行分析：第一階段從生活中的實際現象入手，學生討論、分析、交流，能初步了解什么是平拋運動；第二階段通過運用實驗探究得出平拋運動的特點和規律，構建物理模型，推導平拋運動的速度和位移公式；第三階段運用平拋運動的知識解決實際問題。

（二）學情分析

高一學生已經理解了直線運動，會利用牛頓運動定律分析判斷直線運動的形式，對運動與相互作用觀念形成初步認識。拋體運動將學生的認知從一維空間擴展到二維空間，進一步發展學生的運動與相互作用觀念和運用所學知識解決新問題的能力。本章是培養學生抽象能力和實驗探究能力的重要章節，高一學生已經開始從形象思維向抽象思維過渡，注重從現象到本質的追尋。

生活中的拋體運動、曲線運動的情境比比皆是，之前的直線運動不能很好地解決物理與生活中的很多問題。學生學習拋體運動時，教師可以利用學生的好奇心、探究欲望激發學生的學習興趣，還可以幫助或引導學生建構運用已知獲取未知的臺階，即通過已經學過的直線運動相關概念和規律、牛頓運動定律的知識和數學知識，嘗試通過“化曲為直”的思想，把曲線運動分解成直線運動。

（三）重難點分析

重點：掌握平拋運動的條件、特點以及平拋運動的規律，會運用實驗分析平拋運動在水平方向和豎直方向的特點，并對平拋運動的知識進行總結概括和運用。

難點：引導學生設計平拋運動實驗，并探究其運動特點和規律。

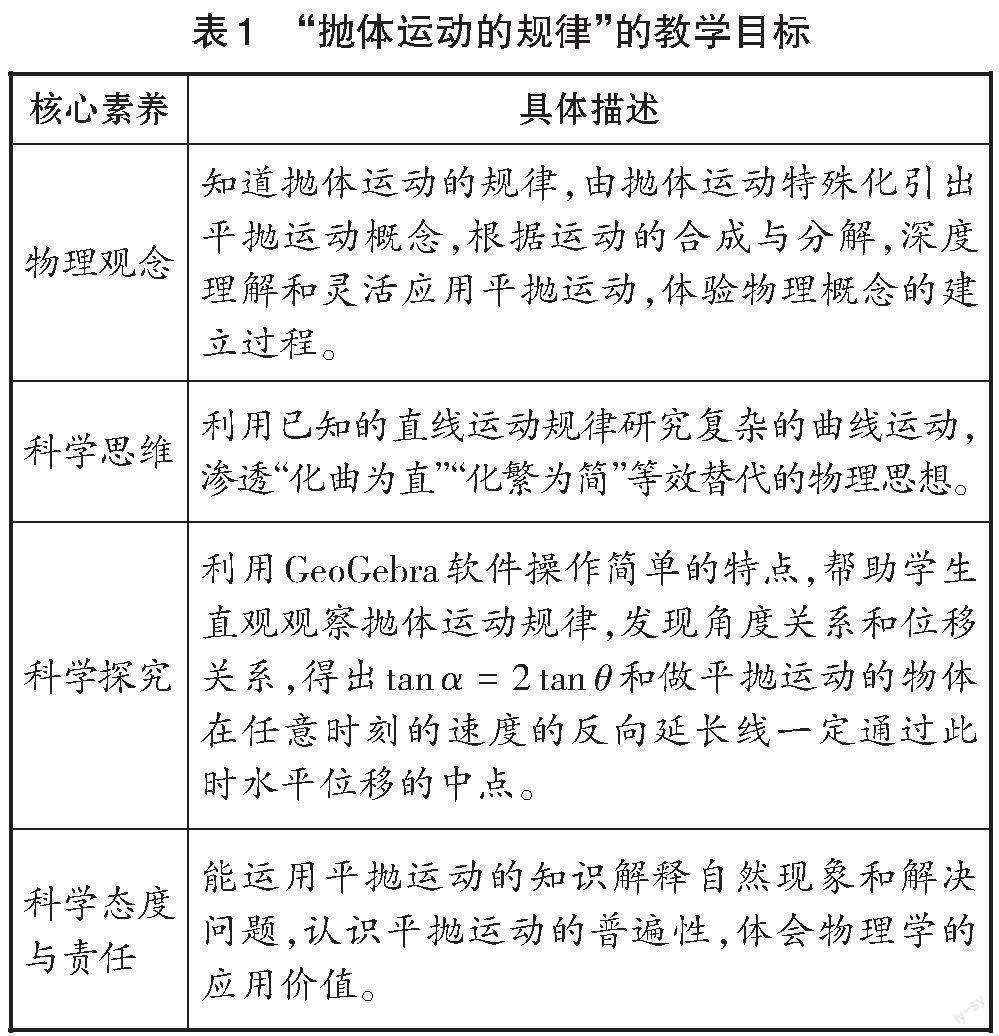
（四）教學目標分析

“拋體運動的規律”的教學目標如表1所示。

（五）教學過程設計

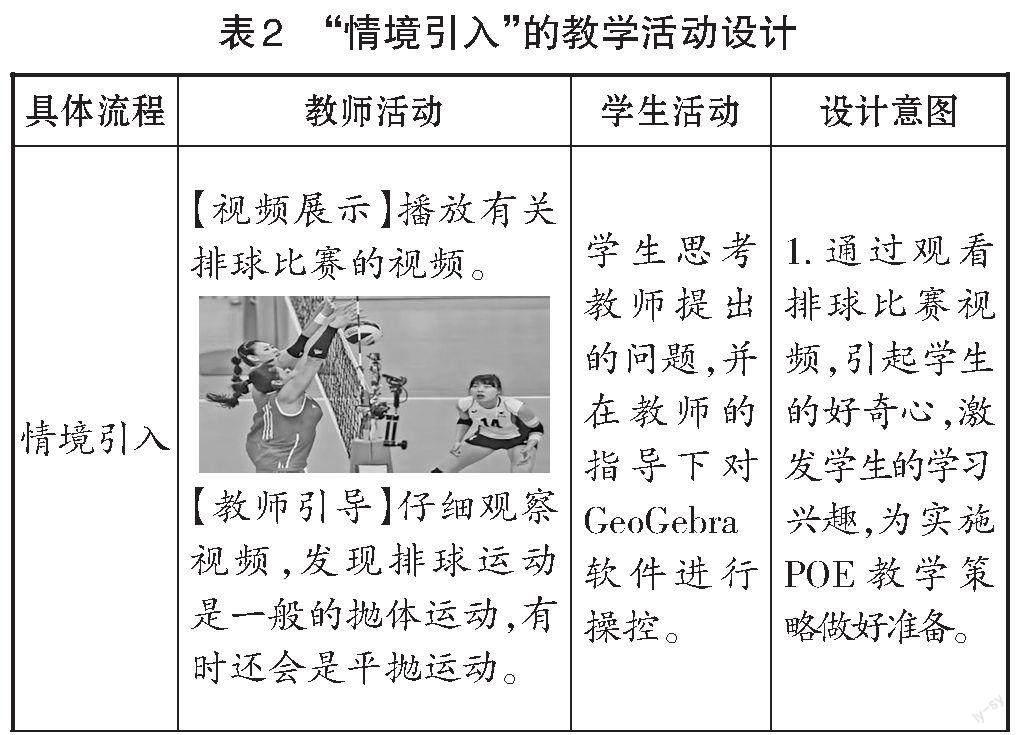
1.情境引入

“情境引入”的教學活動設計如表2所示。

2.在POE教學策略下利用GeoGebra軟件繪制拋體運動的軌跡及呈現其規律。

環節一：預測

預測是POE教學策略的首要環節，是學生基于已有的認識去思考教師提出的問題，它能暴露學生的前概念，在新舊知識之間產生認知沖突，也為教師的教學提供幫助。在預測環節中，學生在教師的幫助下，利用GeoGebra軟件繪制排球的運動軌跡，學生主動參與其中，這樣可以提高學生的學習興趣。“預測”環節的教學活動設計如表3所示。

環節二：觀察

觀察是POE教學策略的中間環節，它是對預測環節進行驗證，學生利用GeoGebra軟件繪制排球的運動軌跡圖、平拋運動的角度關系圖和位移關系圖。在觀察環節中，學生以預測的問題為基礎，利用GeoGebra軟件中的動畫演示進行觀察，研究預測的問題，得出規律。“觀察”環節的教學活動設計如表4所示。

環節三：解釋

解釋是POE教學策略的最后環節，它是對預測和觀察兩個環節進行概括，分析得出的結論是否與預測一致。讓學生全程參與討論交流，提出各自的見解和想法。“解釋”環節的教學活動設計如表4所示。

將POE教學策略應用于探究平拋運動的規律，可以激發學生的學習興趣；在探究的過程中體現了以學生為主體、以教師為主導的教學觀，符合當前提倡的素質教育要求；對學生的語言表達、概括總結、動手操作、邏輯推理有一定的幫助。

GeoGebra軟件可以幫助學生將問題和研究對象更直觀地表示出來，有利于問題的解決。

［? ?參? ?考? ?文? ?獻? ?］

［1］? 林雪梅，張軍朋.“POE”教學策略及其在物理教學中的應用［J］.物理教學探討，2011，29（4）：74-76.

［2］? 周玨誼，張軍朋.POE教學策略在物理教學中的應用：以“決定浮力大小的因素”為例［J］.物理教學探討，2021，39（5）：5-7，11.

［3］? 劉健智，程婷.GeoGebra軟件在物理可視化教學中的應用［J］.物理教師，2021，42（6）：70-73.