到達時間差與掃描時間差定位精度分析

鄧 兵,姚山峰,楊宇翔,賀 青,歐陽鑫信

(信號盲處理國家級重點實驗室, 成都 610041)

0 引言

對于周期性旋轉掃描雷達信號輻射源的定位屬于無源定位的研究范疇之一,長期以來受到國內外眾多學者的關注[1-7]。常用的雷達信號無源定位方法主要包括測向交會定位(angle of arrival,AOA)與到達時間差(time difference of arrival,TDOA)定位2種技術體制[8-13]。其中測向交會定位利用2個以上接收站對雷達信號的來波方向進行測量,然后通過不同的測向線交會得到目標的位置信息。而到達時間差則利用2組以上雷達信號到達不同的接收站路徑差異所帶來的時間差值實現目標輻射源定位。由于以上方法隱蔽性強、實用性好、系統復雜度低等優勢,在實際當中受到廣泛應用。

然而由于測向交會定位精度受限于目標來波方位估計精度,而高精度測向系統往往復雜度較高,對于天線尺寸、構型等有較高要求;時差定位技術需要3站或者3站以上,要求信號能夠多站同時接收,且一般信號時差估計精度受限于接收站所獲取雷達信號的信噪比、帶寬等因素,對于站間同步精度要求高[14]。這些因素制約了測向交會與時差定位2種體制在部分高精度定位需求場合下的使用。

針對靜止或者慢速運動的周期性旋轉掃描雷達輻射源,提出一種基于到達時間差與掃描時間差聯合的無源定位方法。該方法僅需要2個接收站,通過測量2站之間所接收雷達信號的到達時間差(TDOA)和雷達輻射源信號主瓣掃描到2個接收站之間的時間差,即掃描時間差(time difference of scan,TDOS),其中到達時間差(TDOA)確定了一條以2個接收站為焦點的雙曲面,與地球球面相交后,形成了一條到達時間差定位雙曲線;掃描時間差(TDOS)確定了一個到2個接收站夾角為定值的曲面,該曲面以兩接收站連線為弦,以等角度線為弧線組成弓形,繞兩接收站連線對稱旋轉形成,同樣與地球球面相交后,形成了一條定位掃描時差等角度線,雷達輻射源位于到達時間差定位雙曲線和掃描時間差等角度線交點上。

雷達信號到達時間差估計可以通過脈沖描述字(pulse description word,PDW)參數提取,精度較高;掃描時間差可以通過檢測兩站雷達信號幅度隨時間變化曲線的峰值位置估計雷達主瓣信號經過兩接收站的掃描用時,進而獲得掃描時間差信息,該信息簡單易獲得、精度很高[1,10]。因此,通過到達時間差與掃描時間差聯合定位方法不僅定位精度高,而且可以減少傳統時差系統對于接收站的數量需求,相對3站接收,雙站共視接收概率更好保證,提高對于周期性旋轉掃描雷達輻射源信號的定位成功率。

文中首先給出到達時間差與掃描時間差聯合定位基本原理以及定位方程,并給出了閉式求解算法,在此基礎上,推導了該體制定位克拉美羅下限(cramer-rao low bound,CRLB),分析了對目標定位精度有影響的不同因素,最后通過計算機仿真總結出了提高到達時間差和掃描時間差角度信息參數測量精度、增大站間基線長度、減小平臺位置誤差來提升目標定位精度的基本結論,并通過在到達時間差為20 ns、掃描時間差為10 μs(等角誤差約為0.001°)典型值情況下,距離接收站連線中心處450 km處,目標定位精度可以達到50 m,證明了該方法具有很好的實際應用價值。

1 到達時間差與掃描時間差定位原理

1.1 掃描時間差定位原理

周期性掃描雷達通過信號回波提取目標位置及方位信息,其掃描周期 一般固定。通過提取雷達旋轉掃描時天線主瓣經過兩接收站的掃描用時,可以獲取得到雷達輻射源與2個接收站形成的夾角信息,其提取基本原理如圖1所示。

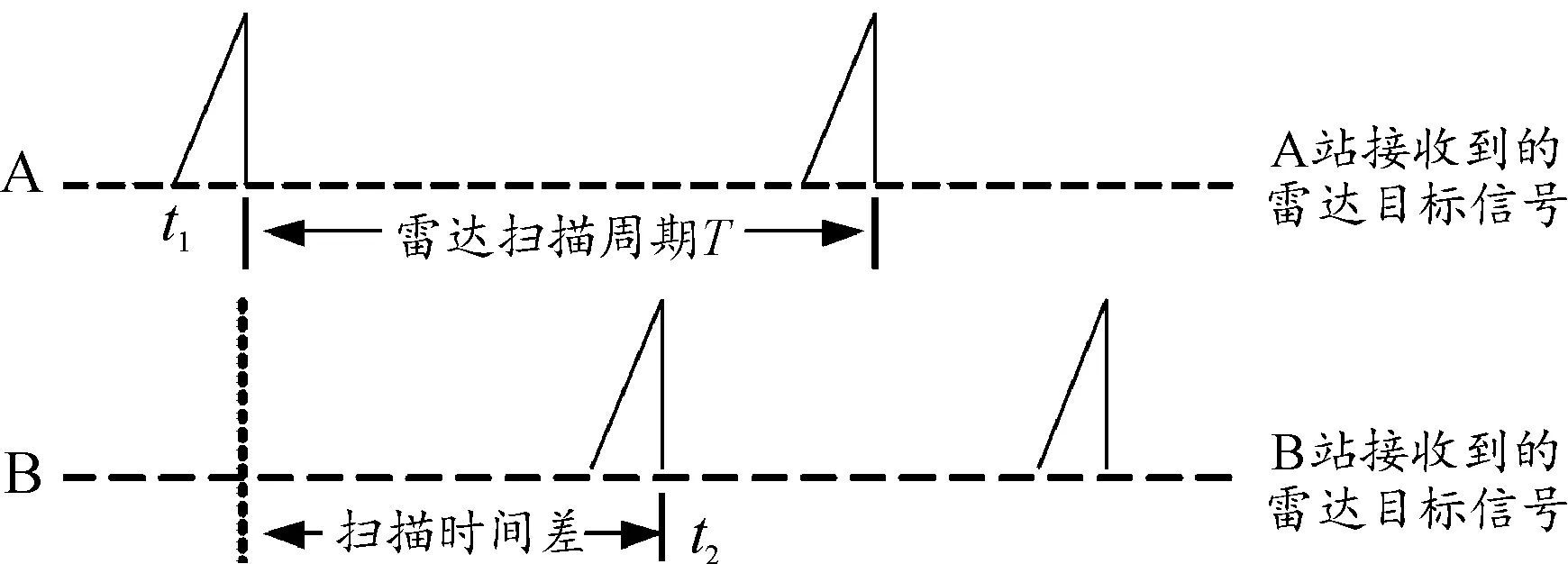
圖1 雷達目標與兩接收站夾角信息示意圖

根據幾何原理,到達2個定點夾角為固定值的點跡不唯一,故利用該夾角信息與地球表面相交,形成一條以2個接收站為端點的圓弧掃描時間差等角線,則目標位于該等角線上。

而對于該夾角θ,其取值區間為[0°,180°]。當θ=0°時,則掃描時間差等角線為以2個接收站為連線的延長線上;當0°<θ<90°時,掃描時間差等角線為遠離2個接收站的近似“8”字圓弧;當θ=90°時,則掃描時間差等角線為以2個接收站為直徑的圓;當90°<θ<180°時,掃描時間差等角線為靠近2個接收站的近似橢圓圓弧;當θ=180°時,則等角線為以2個接收站為連線的線段上。如圖2所示。

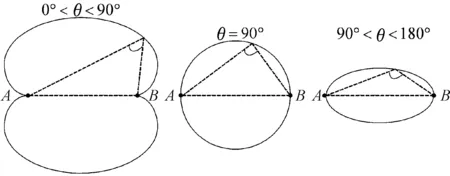
圖2 等角線不同情況示意圖

同時通過提取雷達目標信號到達2個接收站的時差信息,則同樣可以獲得一條到達時間差曲線,聯合獲取的掃描時間差等角線可以實現目標位置求解。其基本原理如圖3所示。

圖3 到達時間差與掃描時間差定位原理示意圖

1.2 定位信息提取方法

1.2.1到達時間差提取方法

對于雷達信號的時差提取分為2種情況:一是當兩站接收信號均為高信噪比的脈沖信號時,提取脈沖的上升沿時間作為脈沖到達時間,然后將兩站接收信號的脈沖到達時間直接相減得到時差;二是當2個接收站中有一站的接收信號為低信噪比的脈沖信號或兩站接收信號為連續波雷達信號時,通過采樣數據二維相關法實現兩站接收信號的到達時間差估計[15-18]。利用以上方法,一般到達時間差測量精度可以到10～50 ns級左右。

1.2.2掃描時間差提取方法

掃描時間差提取方法主要是:對接收信號的幅度包絡進行曲線擬合得到信號幅度隨時間的變化曲線,搜索信號幅度隨時間變化曲線的峰值位置,確定雷達主瓣照射到2個接收站的時刻,由此估計雷達旋轉掃描經過兩接收站的掃描用時,根據掃描用時以及雷達的旋轉方向、旋轉掃描速率計算雷達旋轉掃描經過兩接收站的掃描時間差。

根據該原理可以得到該掃描時間差為

tdos=t2-t1

(1)

式(1)中:t1、t2分別表示雷達信號主瓣到達接收站1、接收站2的時間。

根據雷達掃描周期,可以得到該雷達與2個接收站之間的夾角信息為

θ=|t2-t1|/T*2π

(2)

式(2)中:T為雷達信號掃描周期;θ表示雷達信號與接收站1、2的夾角。當知道雷達旋轉方向或者信號到達兩站先后時,可以去掉|·|符號。

由于雷達掃描周期一般為秒級,而表示雷達信號主瓣到達接收站1、2的時間差(t2-t1)提取精度比較容易可以達到微秒級。

假設雷達掃描周期為3 s,而掃描時間差提取精度為5 μs,則提取的等角信息測量精度約為6×10-4度,可見,該方法能夠獲取很高的等角線測量精度,一般可以達到0.01°～0.000 1°左右。

1.3 定位方程

假設輻射源位置坐標為u=[x,y,z]T,接收站的位置坐標為si=[xi,yi,zi]T,i=1,2。

1.3.1時差定位方程

不失一般性,以接收站1為參考,則根據時差定位原理,可以得到時差方程:

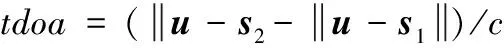
(3)

1.3.2角度定位方程

根據幾何關系,目標信號與接收站1、2之間的夾角為:

(4)

聯合式(3)和式(4)即得到了基于到達時間差與掃描時間差等角信息聯合的目標定位方程:

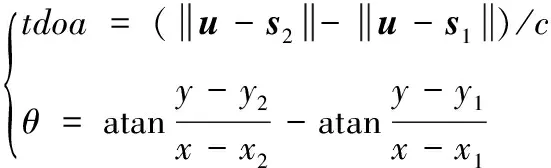
(5)

可以通過上述方程,利用三角余弦定理和幾何關系,推導得到:

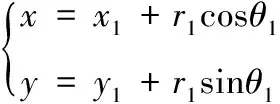
(6)

該解析解復雜度低,可以實時計算出目標位置。

2 定位誤差分析

根據統計信號估計理論,無偏估計量的方差存在理論下界,常用克拉美羅下限(cramer-rao low bound,CRLB)表示[15-20]。并將算法逼近這一下限的程度作為評價各種算法好壞的一個標準。

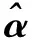
(7)

式(7)中:J為Fisher信息矩陣,其表達式為

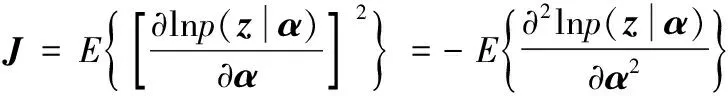
(8)

(9)

令m=[tdoa,θ]T表示到達時間差與掃描時間差等角測量信息。下面根據以上理論來分析到達時間差與掃描時間差等角信息聯合的目標定位克拉美羅界。

2.1 定位誤差與測量誤差的關系

根據式(5),到達時間差與掃描時間差等角信息測量方程兩邊對輻射源坐標位置矢量u微分后可以得出:

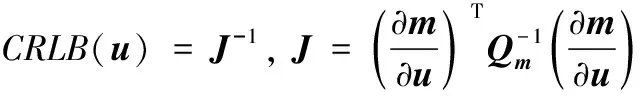
(10)

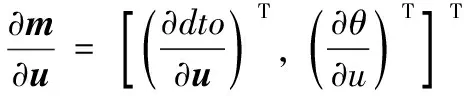
(11)

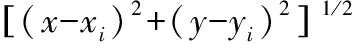
Qm=diag(Qt,Qθ),表示到達時間差與掃描時間差等角信息測量誤差協方差矩陣。

則目標定位的均方根(RMSE)誤差為

RMSE=tr(CRLB(u))

(12)

式(12)中:tr(·)表示取矩陣跡。

2.2 定位誤差與平臺誤差的關系

由于定位過程中,到達時間差、掃描時間差等角信息測量值與平臺的位置相關,若接收平臺自身位置在計算時存在誤差,則該誤差將被引入到目標位置估計過程中,進而使得輻射源位置估計精度受到影響。

進一步推導存在平臺站址誤差時的定位下限。根據相關文獻[19-20],此時的CRLB表達式為:

CRLB(u)=J-1,J=X-YZ-1YT

(13)

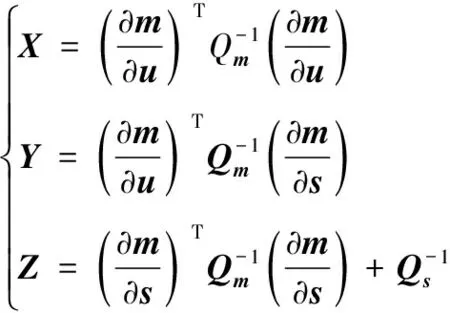
(14)

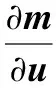
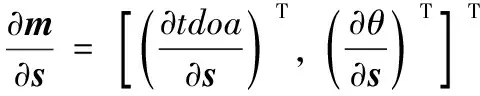
(15)

Qs為對應的平臺位置誤差協方差矩陣。

3 仿真分析

為進一步說明到達時間差與掃描時間差等角信息聯合定位體制中各影響因素對于目標輻射源定位精度的影響,分別從測到達時間差誤差大小、等角信息測量大小、平臺位置誤差大小等方面,進行輻射源定位誤差仿真分析,以便直觀說明這些因素對于定位誤差的影響。

為避免特殊化,假設2個觀測平臺初始位置分別位于(100° E,40° N,0 m)、(101° E,40° N,0 m)處(表1)。

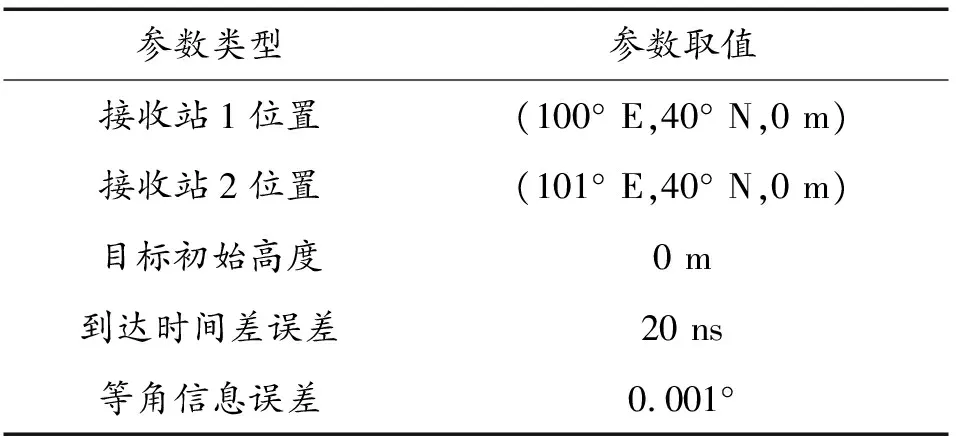
表1 初始仿真參數設置

按照以上參數,仿真得到目標定位GDOP分布,結果如圖4所示。

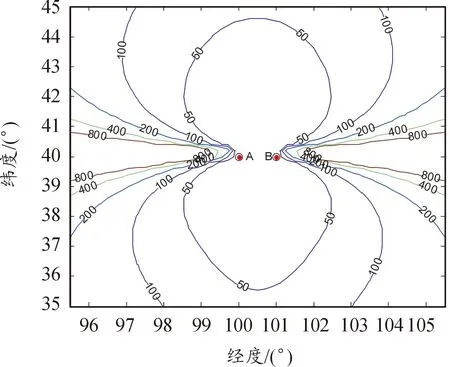
圖4 時差等角線定位誤差GDOP分布圖

從圖4可以看出:

1) 目標定位精度關于2個接收站連線呈上下、左右對稱分布;

2) 目標位置越靠近2個接收站連線垂線方向定位精度越高,然后隨著目標位置的遠離定位精度隨之下降;

3) 目標位于2個接收站連線延長線上時,定位精度最差,離觀測平臺越遠,誤差越大,近乎不可觀測。

4) 在到達時間差為20 ns、掃描時間差為10 μs(等角誤差約為0.001°)典型值情況下,距離接收站連線中心處450 km處,目標定位精度可以達到50 m,遠遠超過目前的時差定位系統。

在對于誤差分布基本情況有所直觀印象下,以定位精度200 m為標準,通過觀察滿足該精度的目標分布方位,進一步分析不同誤差影響因素對輻射源定位精度的影響。

3.1 到達時間差精度影響

首先分析到達時間差測量精度的影響。假設到達時間差測量精度分別為10、20、50 ns。等角信息誤差為0.000 1°,在以上參數假設條件下,200 m定位精度GDOP分布結果如圖5所示。

圖5 不同時差測量誤差條件下GDOP分布圖

從該仿真條件下的GDOP結果圖可以看出:時差測量精度越高,相同位置處的目標定位精度越高。

3.2 掃描時間差等角信息精度影響

分析掃描時間差等角測量精度的影響。假設到達時間差測量精度為20 ns。等角信息測量誤差分別為0.000 1°、0.001°、0.005°。在以上參數假設條件下,200 m定位精度GDOP分布如圖6所示。

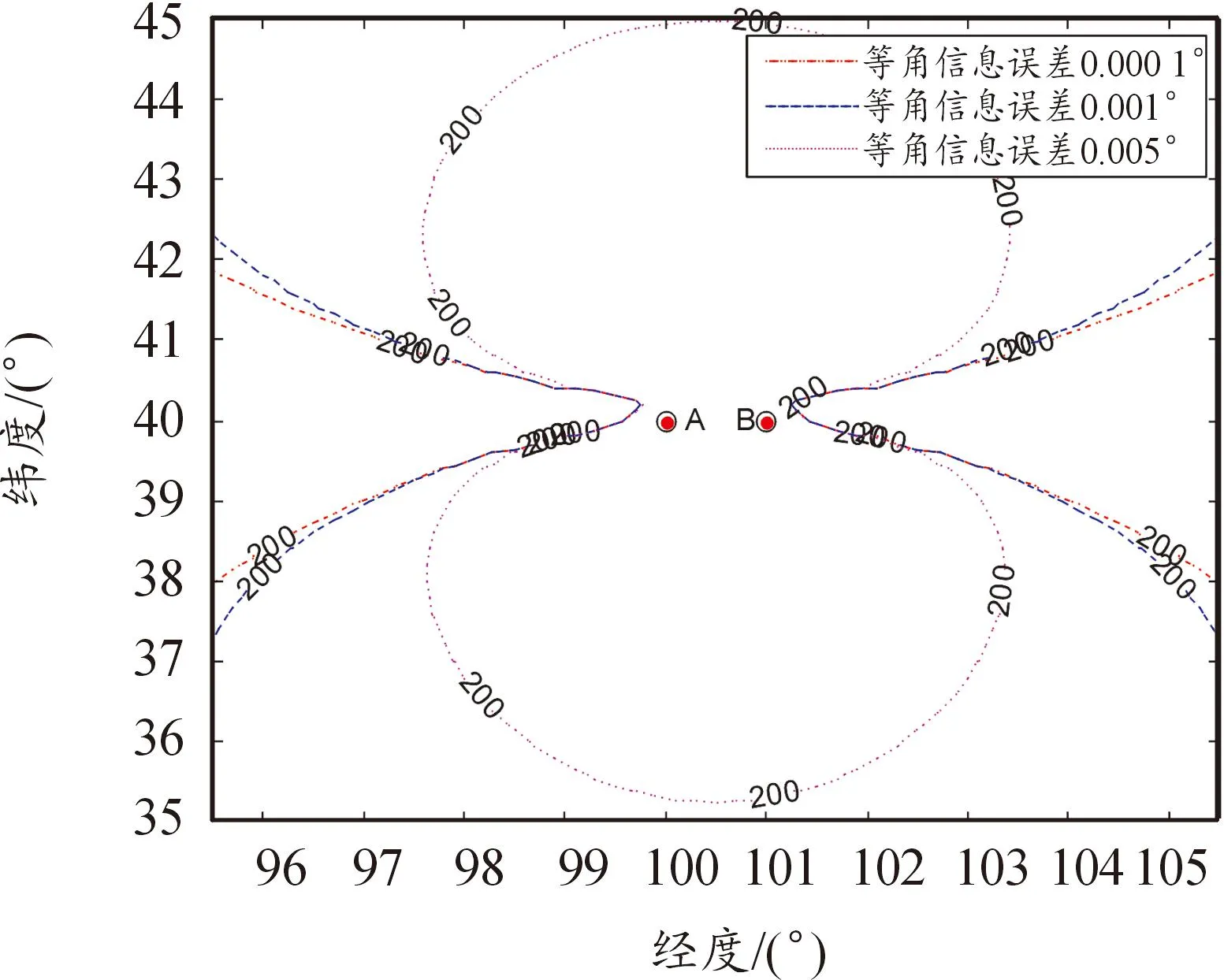
圖6 不同等角測量誤差條件下GDOP分布圖

從該仿真條件下的GDOP結果圖可以看出:等角信息測量精度越高,相同位置處的目標定位精度越高。

3.3 基線長度影響

分析不同平臺基線長度對定位精度的影響。到達時間差測量精度為50 ns,等角信息誤差為0.000 1°,平臺高度0 km。假設平臺基線長度分別為10、50、100 km。在以上參數假設條件下,目標GDOP分布如圖7所示。

圖7 不同基線長度下GDOP分布圖

從該仿真條件下的GDOP結果圖可以看出:相同測量條件下,接收站平臺之間基線越長,相同位置處的目標定位精度越高。

3.4 平臺高度影響

分析不同接收站平臺高度對定位精度的影響。到達時間差測量精度為50 ns,等角信息誤差為0.001°,假設平臺高度分別為0、5、10 km。在以上參數假設條件下,目標GDOP分布如圖8所示。

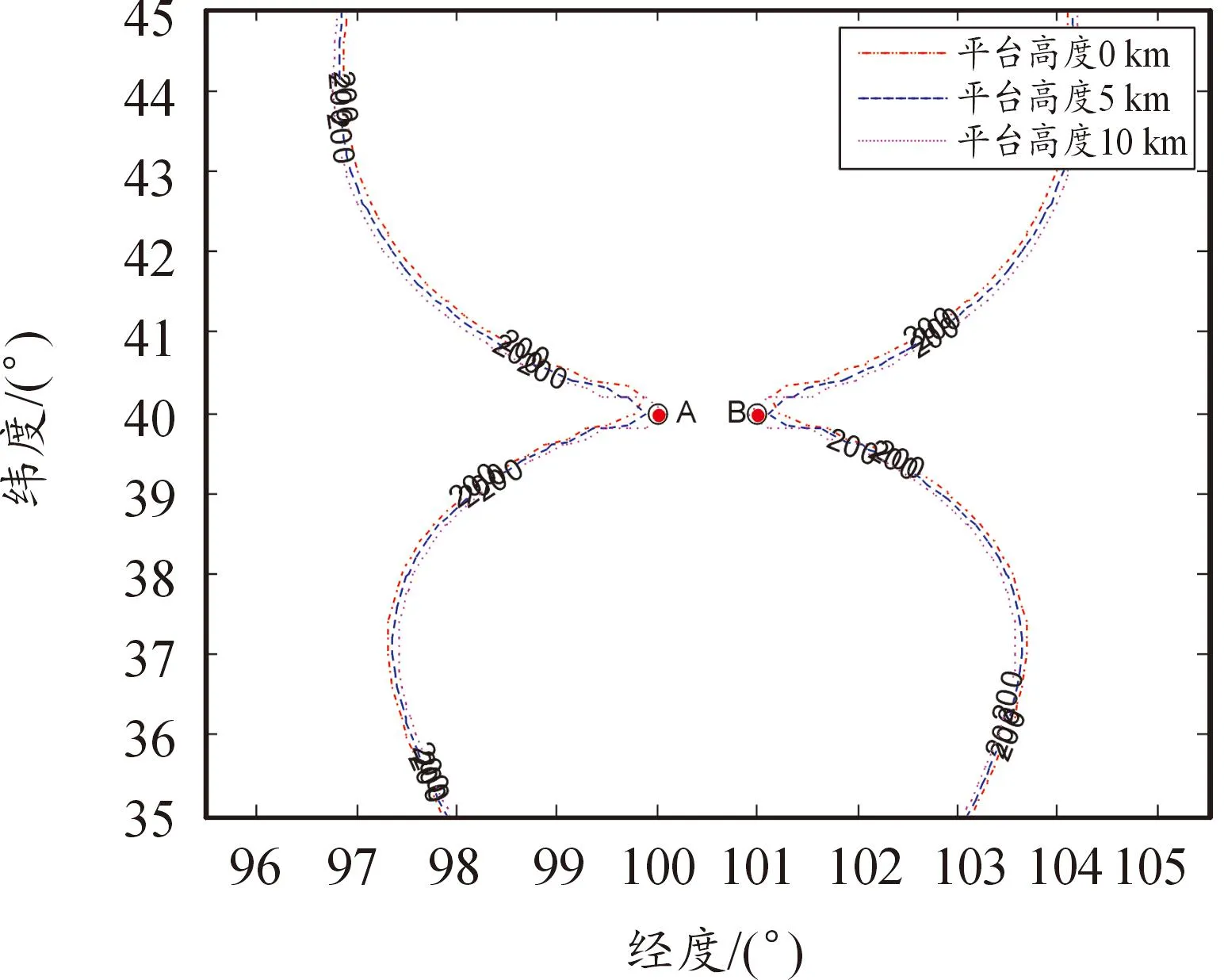
圖8 不同平臺高度條件下GDOP分布圖

從該仿真條件下的GDOP結果圖可以看出:相同測量條件下,接收站平臺高度越高,相同位置處的目標定位精度越高,但是差距不大,在到達時間差、掃描時間差等角信息測量精度高時可以忽略平臺高度的影響。

3.5 平臺位置誤差影響

分析不同接收站平臺位置誤差對定位精度的影響。到達時間差測量精度為20 ns,等角信息誤差為0.001°,假設平臺位置誤差分別為1、5、10 m。在以上參數假設條件下,目標GDOP分布如圖9所示。

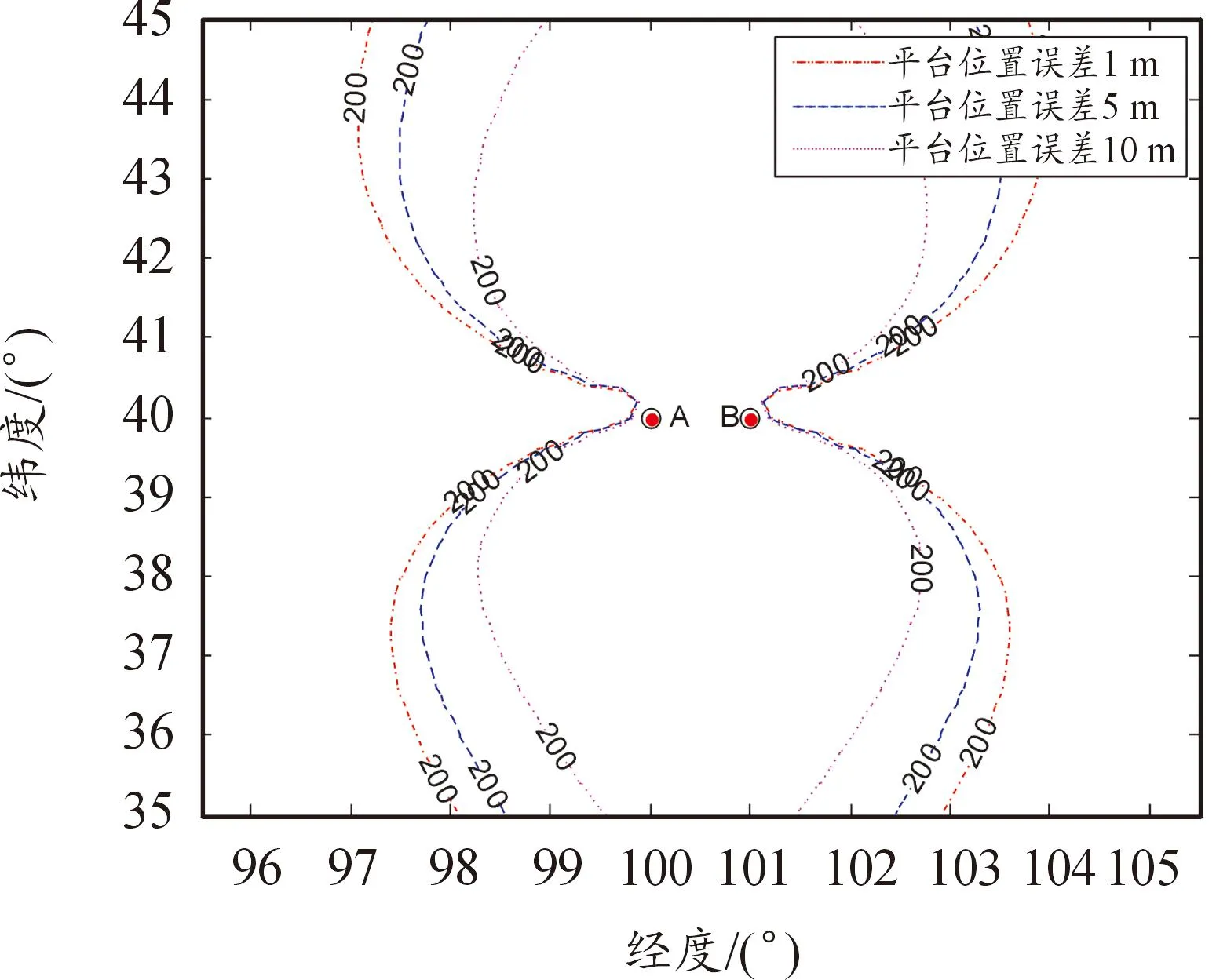
圖9 不同平臺位置誤差條件下GDOP分布圖

從該仿真條件下的GDOP結果圖可以看出:在當前的參數測量條件下,平臺位置誤差越小,相同位置處的目標定位精度越高。

3.6 仿真結論

根據仿真結果可以看出,基于到達時間差與掃描時間差聯合的無源定位當中,通過提高到達時間差和掃描時間差角度信息參數測量精度、增大站間基線長度、減小平臺位置誤差等都能夠明顯提升目標定位精度。

進一步分析可以看出,提高到達時間差和掃描時間差角度信息參數測量精度均是從測量信息入手,越精確的測量參數表明對于目標的信號特征參數估計地越準確;減小平臺位置誤差等主要是降低定位解算中直接相關的誤差項,進而降低目標定位誤差。

4 結論

基于雙站到達時間差和掃描時間差信息的掃描型輻射源定位系統,相對三站時差定位系統,減少了觀測站數目需求,便于靈活布站選址,是一種簡單有效的無源定位手段。

下一步,將進一步利用以上定位模型、誤差定位克拉美羅界,指導實際系統的信號接收及參數提取、高精度定位算法以及運動接收平臺下的目標定位等展開研究工作。