基于EW-AHP改良未確知測度理論的泥石流危險性評價方法

賈世濟，孫 碩，高 帥

1.河北地質大學 城市地質與工程學院，河北 石家莊 050031；2.滄州交通學院 土木建筑工程學院，河北 滄州 061100

0 引言

泥石流的危害巨大且誘因眾多，相較崩塌、滑坡和洪水等單一災害，其破壞范圍更加廣泛，破壞程度更加嚴重[1]。泥石流危險性對于把握泥石流整體特征、預測泥石流危害具有十分重要的作用，因此，開展泥石流危險性評價研究、合理地進行危險等級劃分非常重要，是泥石流防災減災研究的重點和難道。

中國對泥石流危險性評價的研究始于20世紀80年代初，研究歷經定性分析—定性打分—定量計算，研究指標也從單一評價過渡到多指標綜合評價，使泥石流危險性評價有了較為長足的發展[2]。但整體上仍然存在許多半經驗半理論評價內容，尤其對于各評價指標賦權問題上，仍然存在不合理因素。近年來，不確定分析方法在泥石流危險性評價研究中得到了迅猛發展，如灰色關聯度、支持向量機、隨機信息理論、模糊綜合評價等[3]，這些方法拓展了泥石流危險性的研究思路，但均存在一定待完善之處。

泥石流危險性評價的影響因素極其復雜多樣，既有地質體內外因素，又有外部誘因。所以，如何建立科學合理的評價體系，并進行有效的危險性評價，是泥石流危險性研究面臨的重要問題。未確知測度理論是由王光遠提出的一種不確定性信息分析理論[4]，未確知測度評價模型能處理多種不確定性信息，在地質災害領域已經取得了一定效果。

合理確定泥石流危害主影響因素的權重是建立評價模型的關鍵，本文嘗試利用EW-AHP組合賦權確定權重，建立基于未確知測度理論的泥石流危險性評價模型，為此種災害的防治研究探索一條新的路徑。

1 組合賦權的未確知測度原理

1.1 單指標測度

將待評價的m個指標I1，I2，…，Im，指標空間I={I1，I2，…，Im}分別劃分出s個危險性評價等級{c1，c2…cs}，根據各指標危險性等級分別確定m個測度函數，待測的m個指標根據對應測度函數計算后可分別得出相應的評價向量{βi1，βi2，βi3…βis}，各評價向量組成單指標評價矩陣，如下式所示。

(1)

1.2 EW-AHP的組合賦權

1.2.1 層次分析法

通過層次分析，可以把多個因素有機地結合起來，創造出一個多維度的分析框架，需要完成以下幾個步驟：①構建層次架構；②通過建立一個框架，把問題的每一部分細化成若干層次，并且詳細描述它們之間的相互聯系(表1)；③構造判斷矩陣(表2)[5，6]；④考查層次分析的效果。

表1 確定元素的 1-9 標度方法Table 1 1-9 scaling methods of the elements of the judgment matrix

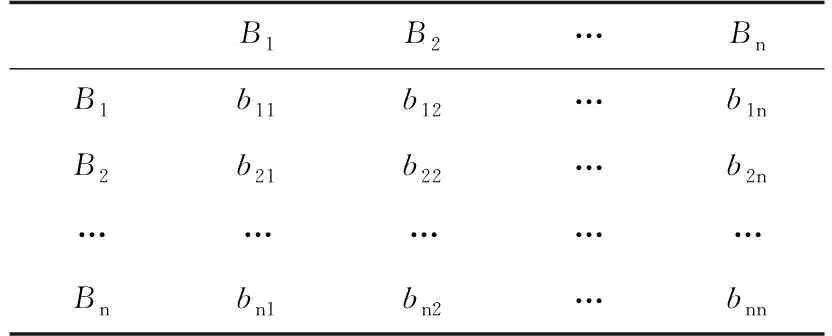
表2 判斷矩陣的形式Table 2 Form of judgment matrix

歸一化處理矩陣最大特征根λmax和自身特征向量，得到評價指標權重集W：{w1，w2，…，wn}。

一致性指標(CI)的計算式為：

(2)

結果CR=CI/RI判斷標準(表3)：CR<0.1，矩陣一致性良好，認為合理；CR=0.1，矩陣一致性良好，認為合理；CR>0.1，矩陣不符合一致性原則，需重新調整，直到結果滿意。

表3 平均隨機一致性指標(RI)Table 3 Mean Random Consistency Index (RI)

1.2.2 熵權法

將待評價指標進行無量綱化處理，可根據測度評價矩陣中的βij估算各指標的信息熵值：

《湖南省建設教育強省規劃綱要（2010～2020年）》（湘發［2010］22號）也明確指出：“將教育信息化納入‘數字湖南’建設體系，以教育信息化促進教育內容、教學手段和方法現代化”，教師運用數字化教學資源開展教學活動已成為一種趨勢。

(3)

用Wij表示指標的權重：

(4)

1.2.3 EW-AHP組合賦權

組合賦權是將熵權法和層次分析法得出的權重值進行耦合，運用乘法合成歸一的方法得出更加科學的綜合權重[7-10]，即：

(5)

1.3 多指標綜合測度

將組合賦權得到的綜合權值Wj與單指標評價矩陣相乘，即：

βe=βij×Wj

(6)

其中βe={β1e，β2e，…，βse}；∑βie=1，{β1e，β2e，…，βse}為評價向量。

1.4 置信度識別

考慮到評價等級劃分的有序性，需將置信度作為識別準則。設置信度為λ(λ≥0.5)。

2 單溝泥石流危險性評價模型

2.1 區域概況

2.2 構建測度函數

本文將使用7個關鍵因素來評估武都區兩水村的泥石流風險，包括：一次泥石流最大沖出量、流域面積、主溝長度、流域相對高差、泥沙補給段長度比、24 h最大降雨量、人口密度[11](表4)。

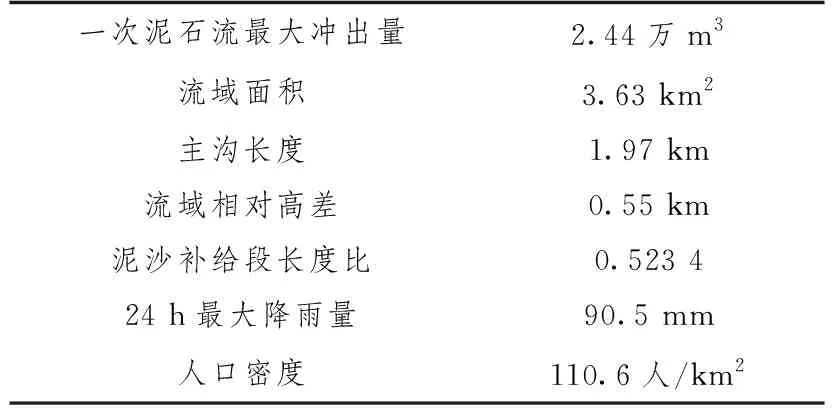
表4 待評泥石流溝評價指標取值Table 4 Evaluation index of debris flow ditch to be evaluated

通過對流域面積等7個指標參照表1進行評價指標等級劃分。

根據表5[12]繪制了7個評價指標測度函數(圖1—圖7)。

圖1 泥石流規模/104 m3Fig.1 Debris flow scale

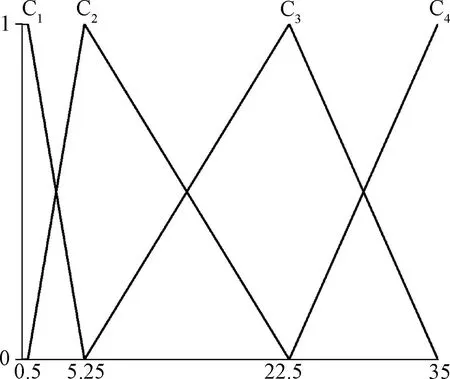
圖2 流域面積/km2Fig.2 Watershed area

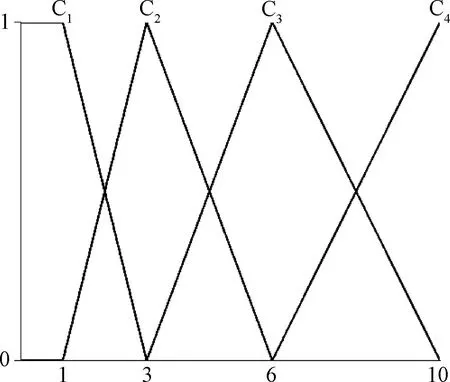
圖3 主溝長度/kmFig.3 Main trench length

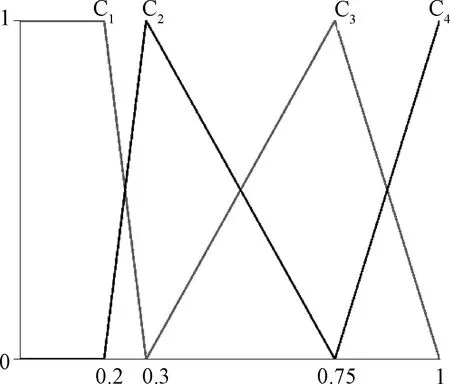
圖4 最大相對高差/kmFig.4 Maximum relative height difference

圖5 泥沙補給長度比Fig.5 Sediment replenishment length ratio

圖6 24 h最大降雨量/mmFig.6 24 h maximum rainfall

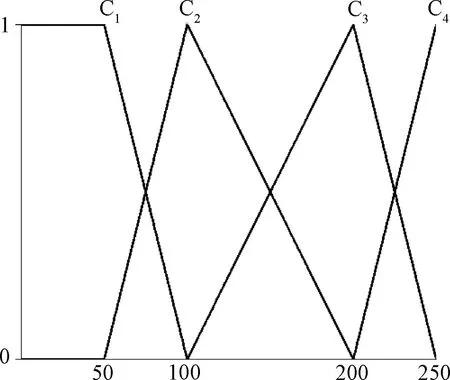
圖7 人口密度(人/km2)Fig.7 Population density

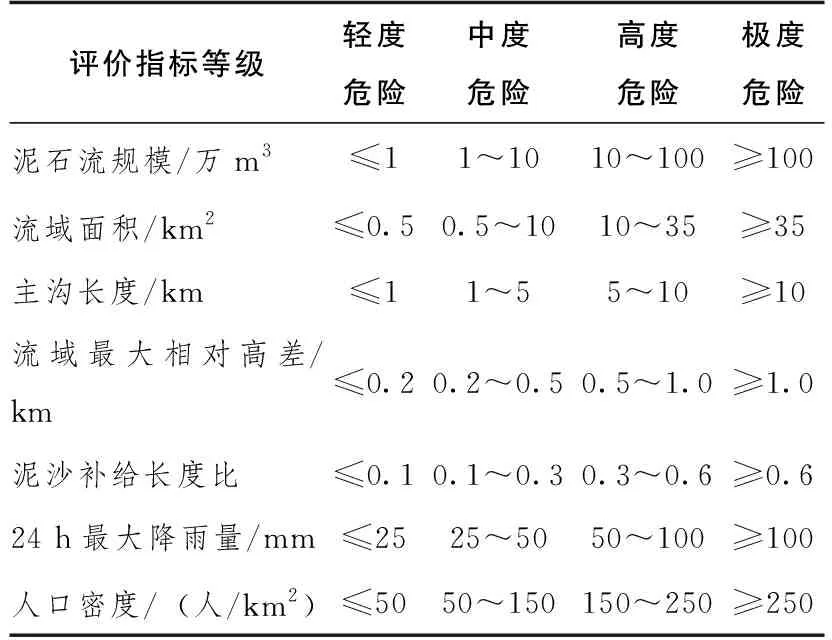
表5 泥石流危險性評價指標等級Table 5 Debris flow risk evaluation index grades

表4評價指標代入相應測度函數，得評價向量。本例流域面積3.63 km2，據相應測度函數(圖2)得：

(7)

將流域面積值x=3.63帶入式 (7)，可得關于流域面積的評價向量(0.336 8，0.663 2，0，0)。依次類推，可得出整個泥石流的評價矩陣βij：

2.3 組合確權

2.3.1 層次分析法賦權

通過分析以上7個指標，我們可以建立一個判斷矩陣來進行分析(表6)：

表6 判斷矩陣Table 6 Judgment matrix

B1表示一次泥石流最大沖出量；B2表示流域面積；B3表示主溝長度；B4表示流域相對高差；B5表示泥沙補給段長度比；B6表示24 h最大降雨量；B7表示人口密度。

利用方根法求得判斷矩陣的特征向量為：3.556 7，2.429 7，1.303 7，1.017 0，0.615 1，0.442 7，0.320 5。

特征向量歸一化可獲7種指標權重：WA={0.367 3，0.250 9，0.134 6，0.105 0，0.063 5，0.045 8，0.033 7}。矩陣的最大特征值λmax=7.663 1；判斷矩陣一致性：

則隨機一致性比率：CR=CI/RI≤0.1 ，判斷矩陣一致性良好。

2.3.2 熵權法賦權

利用信息熵計算各評價指標權重，熵值越大，表示該指標對泥石流危險性給貢獻越大。根據以上(1)式(2)式得出各指標權重：WE={0.137 8，0.136 0，0.125 8，0.126 9，0.125 8，0.159 1，0.190 2}。

2.3.3 EW-AHP組合賦權

根據(3)式合成歸一，兩種權向量耦合可得最終權重向量為：Wj=(0.370 5，0.249 7，0.123 7，0.097 4，0.058 5，0.053 4，0.046 9)。

2.4 確定綜合測度評價向量

將權重向量代入(4)式βe=βij×Wj，可得該泥石流溝的多指標綜合測度向量βe=(0.399 7，0.430 4，0.131 3，0.039 7)。

2.5 置信度識別

取置信度λ=0.5，根據該泥石流溝的多指標綜合測度結果置信度識別準則，該泥石流危險性評價結果為中度等級，與勘察報告相比，結論基本一致。

3 結論

針對泥石流危險性評價中諸多影響因素的不確定性，通過研究7項可能會影響泥石流危害性的因素，構建出一個未確知測度函數，更準確地評估這些因素的作用。此外，我們還采用熵權和層次分析法對指標權重綜合賦權，將客觀因素與主觀因素相結合，更好地反映出泥石流的風險特征。

綜合考慮隴南市武都區兩水村大灣溝泥石流特征，通過應用EW-AHP和未確知測度理論，構建了一個新的泥石流危險性評估模型，能夠提供更加客觀準確的評估結果，表明本模型對泥石流危險性評價在理論和現實層面都有重要意義，是泥石流危險性評價研究中的一條新途徑。