高滲透率下基于并網逆變器阻抗重塑的鎖相環設計方法

楊 明 楊 倬 李玉龍 趙月圓 朱 軍

高滲透率下基于并網逆變器阻抗重塑的鎖相環設計方法

楊 明 楊 倬 李玉龍 趙月圓 朱 軍

（河南理工大學電氣工程與自動化學院河南省煤礦裝備智能檢測與控制重點實驗室 焦作 454003）

針對鎖相環、電網阻抗與并網逆變器相互耦合所引發的系統穩定性下降問題。首先，建立考慮電網阻抗的鎖相環控制結構模型，通過分析鎖相環閉環傳遞函數可知，電網阻抗會使鎖相環系統產生右半平面閉環極點，嚴重影響鎖相環與逆變器系統的穩定性。其次，通過分析逆變器系統輸出阻抗，說明鎖相環所引入的負阻抗是逆變器系統穩定裕度下降的主要原因。鑒于此，該文提出一種新型鎖相環設計方法，理論分析表明，所提方法既能夠保證高滲透率下鎖相環具有高魯棒性，又能夠對逆變器系統輸出阻抗進行重塑，有效拓寬系統對電網阻抗的適應范圍。最后，通過仿真與實驗驗證所提新型鎖相環設計方法的有效性。

高滲透率 并網逆變器 鎖相環 阻抗重塑 魯棒性

0 引言

目前，隨著光伏、風電等新能源發電技術與裝機容量的不斷提高，高滲透率新能源發電已成為必然趨勢，此時，電網往往表現出低短路比的弱電網特性甚至極弱電網特性，即含有不可忽略的電網阻抗，因此，通常可以由最大短路比（Short Circuit Ratio, SCR）的大小來判斷出電網的強弱，從而間接地判斷出新能源發電系統滲透率的高低[1-3]。基于鎖相環（Phase-Locked Loop, PLL）同步控制的并網逆變器是新能源發電的重要組成部分，其穩定性往往受到電網阻抗與PLL的影響[4-5]。因此，高滲透率下PLL對并網逆變器穩定性影響的分析與研究是十分必要的。

弱電網下，并網公共耦合點（Point of Common Coupling, PCC）電壓作為PLL的輸入信號，由于其受電網阻抗的影響，間接導致PLL穩定性受電網阻抗的影響[6]。高滲透率下PLL對并網逆變器穩定性影響的研究可分為兩個方面：一是對PLL控制結構而言，電網阻抗的存在使PLL結構引入了額外的反饋回路，對PLL自身魯棒性產生影響；二是逆變器系統考慮PLL時，系統輸出阻抗會引入與PLL相關的負阻抗，此負阻抗直接影響系統輸出阻抗的幅值、相位，導致并網逆變器系統穩定裕度下降。

目前，針對上述問題，許多學者采用不同的分析方法進行了研究。文獻[7-8]通過對并網逆變器系統阻抗模型進行分析，提出了在傳統PLL前串聯二階低通濾波器或復數濾波器的設計方法，從而降低逆變器輸出阻抗分母中與鎖相環相關的附加項對逆變器穩定性的影響。但上述兩種方法會引入額外的相位補償或濾波能力不足的問題。文獻[9-10]提出了一種基于電網阻抗在線測量的自適應控制策略，可有效解決電網阻抗較大時并網系統的失穩問題，但此方法過度依賴電網阻抗在線測量的準確性。在文獻[11]所提對稱PLL結構基礎上，文獻[12]提出了一種基于復數濾波器的對稱鎖相環同步結構，所提方案在不增加額外控制補償和調整系統控制參數前提下，實現了并網逆變系統頻率解耦控制。文獻[13]通過對文獻[7]所提新型PLL結構進行分析，提出了一種基于電流二階校正的阻抗重塑方法，該方法通過約束二階校正環節參數，實現了并網逆變器單位功率因數并網與穩定運行。文獻[14-15]對逆變器系統等效輸出阻抗進行重塑，提高其與電網阻抗交截頻率處的相位裕度。上述研究表明，弱電網下，雖然基于傳統PLL的改進型PLL結構與控制策略多種多樣，但電網阻抗所導致的PLL自身魯棒性下降問題仍未被充分研究，因此，高滲透率下PLL系統與逆變器系統穩定性的交互影響仍需進一步研究。

基于上述研究現狀，本文以弱電網下單相LCL濾波并網逆變器為研究對象，通過深入揭示鎖相環自身魯棒性與逆變器系統穩定裕度下降的原因，提出了一種以并網點電壓、并網點電流為輸入信號的新型鎖相環控制結構，所提新型鎖相環控制結構不僅自身具有高魯棒性，而且能夠對系統輸出阻抗相位特性進行重塑，極大地提高了并網逆變器系統在弱電網甚至極弱電網下的穩定性。最后，通過仿真與實驗驗證了本文理論分析的正確性以及所提新型鎖相環設計方法的有效性。

1 弱電網下逆變器系統穩定性分析

1.1 LCL濾波并網逆變器的數學模型

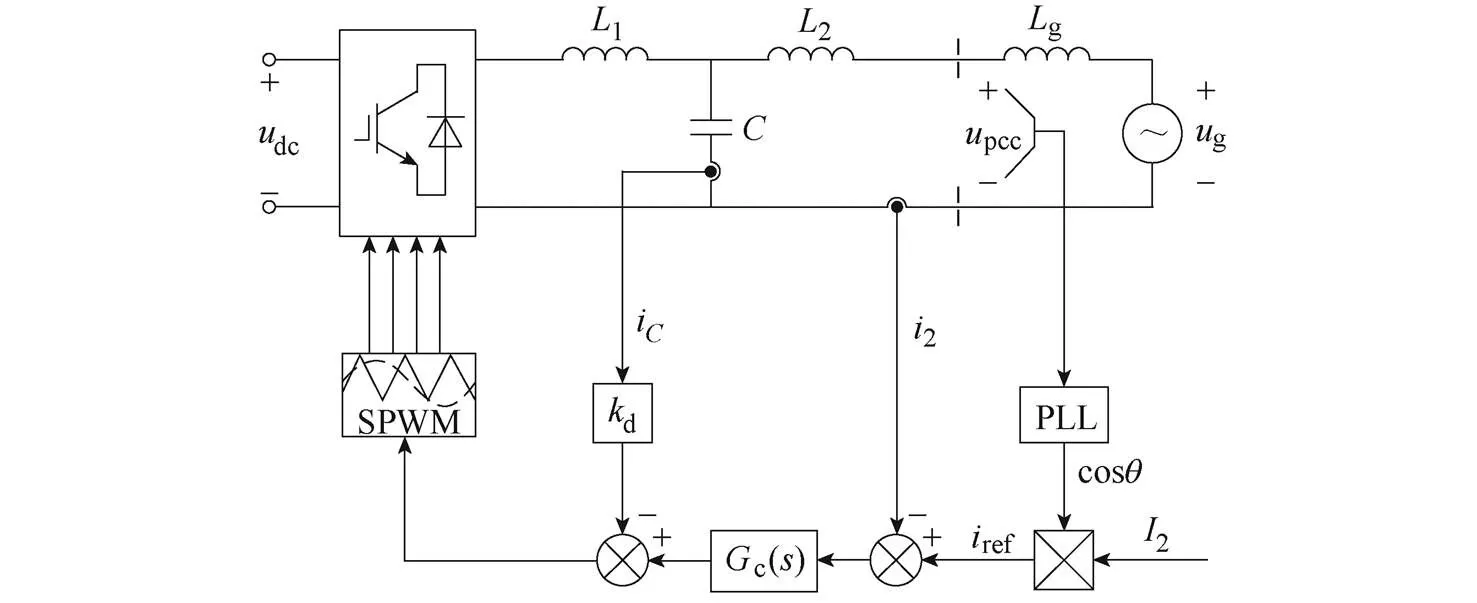
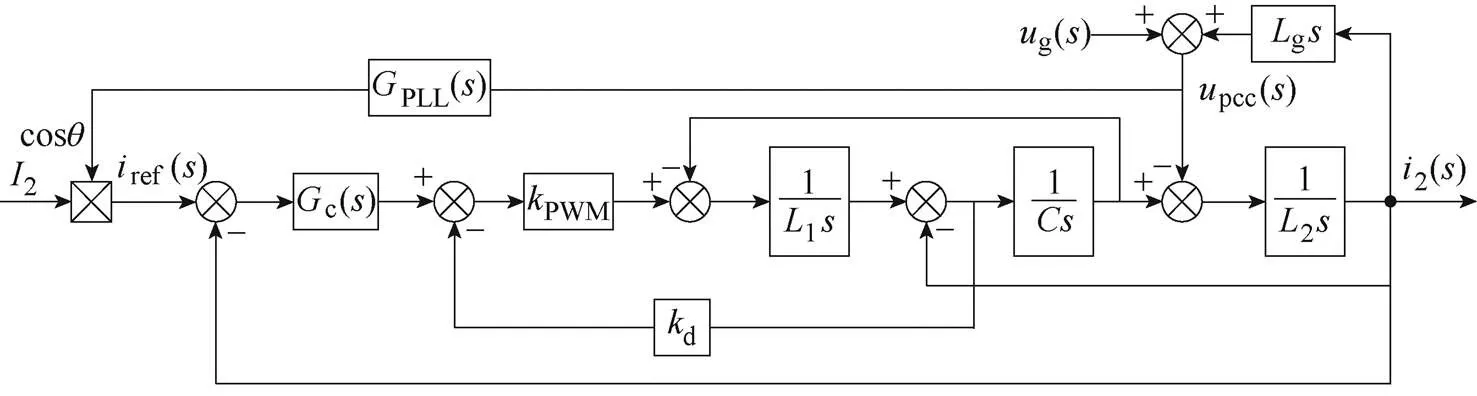
圖1為采用并網電流反饋和電容電流有源阻尼策略的單相并網逆變器的拓撲結構和控制框圖。

（a）拓撲結構

（b）系統控制框圖

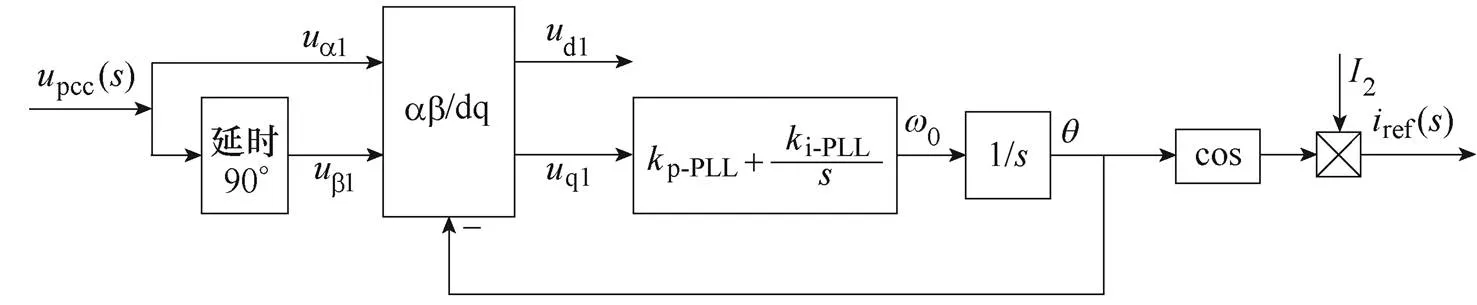
（c）傳統PLL控制結構

圖1 單相并網逆變器的拓撲結構和控制框圖

Fig.1 Topology structure and control block diagram of single-phase grid-connected inverter

圖1中，逆變側電感1、濾波電容和網側電感2構成LCL濾波器；電網等效為電壓源與電網阻抗串聯的等效模型，g為電網電壓，g為電網阻抗（本文考慮最惡劣情況，即電網阻抗為純電感）；dc、pcc分別為直流母線電壓、PCC處電壓；1、2、i分別為逆變器機側電流、并網電流、濾波電容電流；ref、2分別為并網電流基準值、給定幅值；為PLL輸出相位（PCC處相位），p-PLL、i-PLL分別為PLL控制器的比例系數、積分系數；d為電容電流有源阻尼系數；c()為電流控制器，本文采用準比例諧振（Quasi Proportional Resonant, QPR）控制器對電流進行控制。

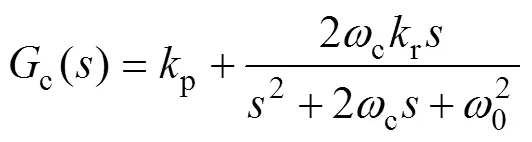
式中，p、r、0、c分別為QPR控制器的比例系數、諧振系數、諧振角頻率和控制帶寬。

此外通過文獻[8]可知，傳統PLL控制環節的傳遞函數表達式為

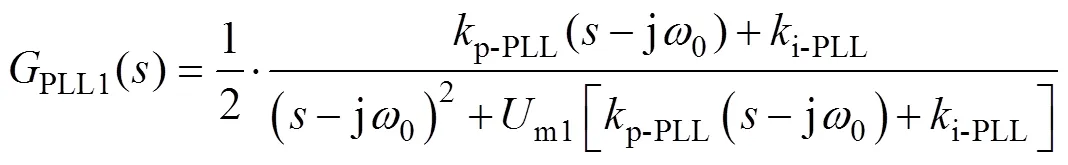
式中，m1為并網點電壓pcc的幅值。

弱電網下，由于電網阻抗不可忽略，當并網逆變器系統考慮鎖相環時，為保證系統穩定性，不僅要考慮鎖相環自身的穩定性，還需要考慮系統輸出阻抗在交截頻率范圍內的穩定裕度。

1.2 弱電網下傳統PLL穩定性分析

根據圖1a可知，強電網下，PLL輸入信號為電網電壓g()，弱電網下，由于受電網阻抗的影響，PLL輸入信號為并網點電壓pcc()，即

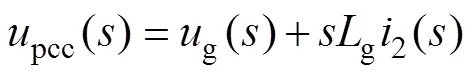
根據式（3）并結合圖1c可得，PLL輸入信號pcc()與a1b1之間的時域關系表達式為

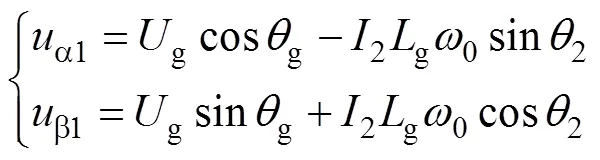
式中，g、g為g()的幅值和相位；2為并網電流2相位；g0為電網阻抗模值。

進一步地，對式（4）進行ab-dq坐標變換可得

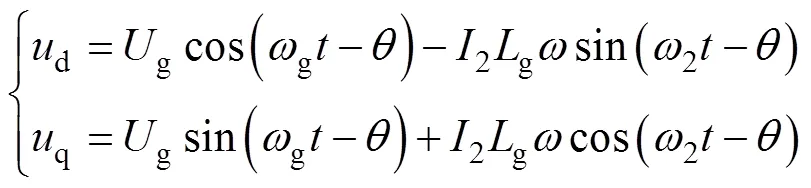
式中，g、2分別為電網電壓和并網電流的角頻率，且有g=g、2=2。

考慮到系統穩定運行時，PCC與電網電壓相位差較小，與并網電流相位一致，即g-q≈0，2-=0，因此，式（5）中分量q1可簡化為

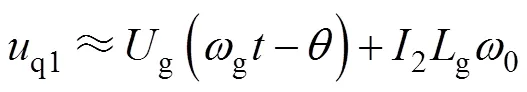
根據式（6）和圖1b可得如圖2所示的弱電網下傳統PLL控制系統框圖。

由圖2可知，弱電網下傳統PLL輸出相位對參考輸入相位g的閉環傳遞函數1()表達式為

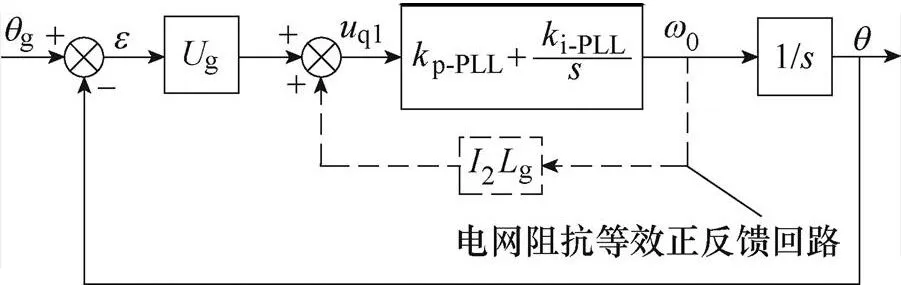
圖2 弱電網下傳統PLL控制系統框圖

通過式（7）可以分析出：PLL控制系統的閉環極點分布受電網阻抗影響，當電網阻抗寬范圍變化時，PLL控制系統會產生右半平面的閉環極點，從而導致PLL系統失穩。此外，結合式（3）和圖2分析可知，正是由于PLL輸入信號中存在分量g2，導致PLL控制環路中引入一條與電網阻抗有關的正反饋回路，此反饋回路直接改變了傳統PLL的控制結構，進而影響了PLL輸入輸出閉環傳遞函數及其自身穩定性。

1.3 弱電網下系統輸出阻抗穩定性分析

由圖1b所示的系統控制框圖可以推導出并網電流2()表達式為

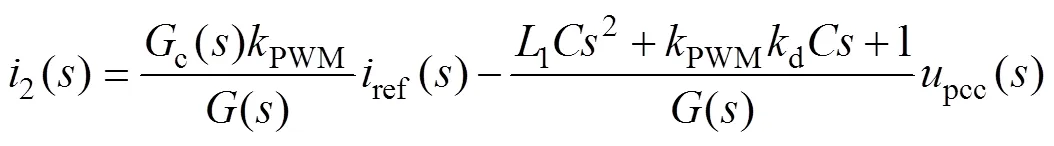
其中

()=123+PWMd22+(1+2)+c()PWM

此外，考慮PLL因素時，由于參考電流ref()=2PLL1()pcc()，將其代入式（8）化簡可得

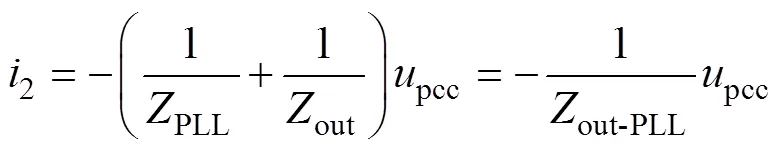
式中，PLL為考慮PLL時所引入的負阻抗；out為不考慮PLL時的系統輸出阻抗；out-PLL為考慮PLL時的系統輸出阻抗。

根據式（9）可得，考慮PLL時的并網逆變器等效電路，out-PLL()、PLL()的表達式分別為

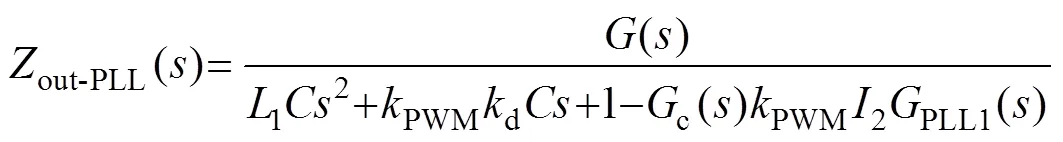
令式（10）中的PLL1()=0即為不考慮PLL時的系統輸出阻抗out。

由文獻[16]可知，并網逆變器系統穩定條件為系統相位裕度（Phase Margin, PM）大于0 °，即要求系統輸出阻抗在交截頻率處的相位必須大于-90 °。根據式（10）、式（11）并結合表1所示參數，可繪制out-PLL、out和PLL的伯德圖如圖3所示。

表1 并網逆變器相關參數

Tab.1 Relevant parameters of grid-connected inverter

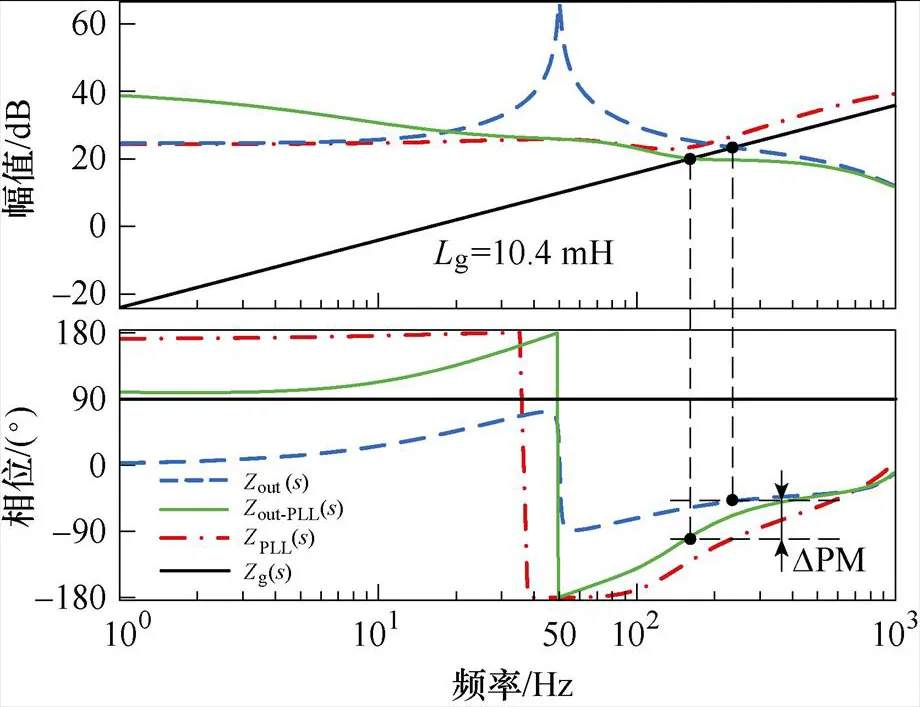
圖3 Zout(s)、Zout-PLL(s)、ZPLL(s)的伯德圖

根據式（9）可知，阻抗out-PLL等效為負阻抗PLL與阻抗out二者并聯所得。由圖3可以看出，在50～1 000 Hz頻率范圍內，負阻抗PLL的相位均小于阻抗out的相位，因此，相較于阻抗out，阻抗out-PLL在交截頻率處的相位大幅下降，且下降角度為DPM。

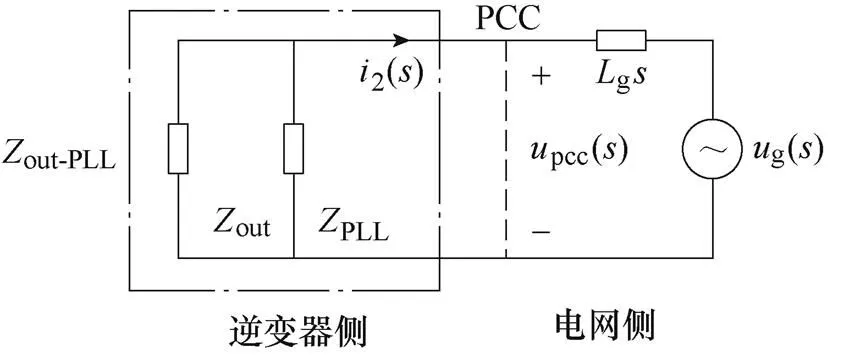
考慮PLL時的并網逆變器等效電路如圖4所示。基于上述分析可知，當電網阻抗寬范圍變化時，考慮PLL時所引入的負阻抗PLL會導致系統在中低頻段穩定裕度大幅降低甚至失穩。為降低負阻抗PLL對系統穩定性的影響，本文提出以下兩種方法：

（a）未阻抗重塑

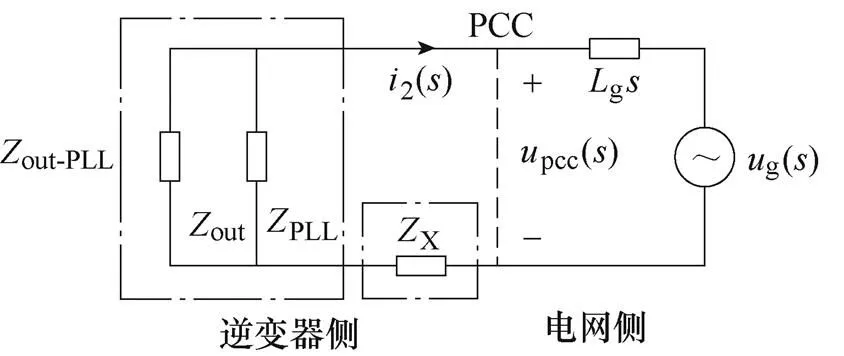
（b）通過串聯阻抗進行阻抗重塑

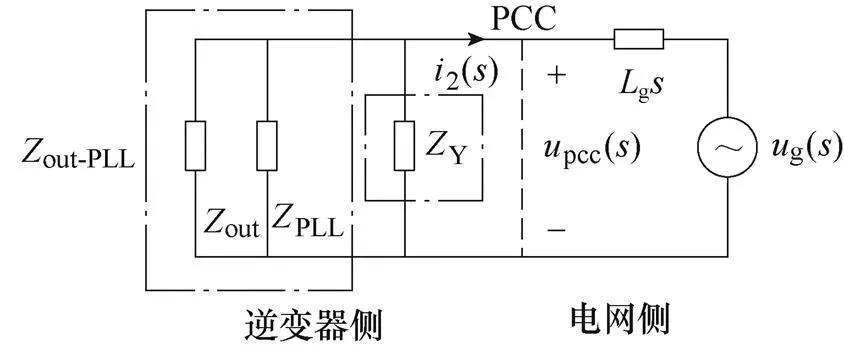
（c）通過并聯阻抗進行阻抗重塑

圖4 考慮PLL時的并網逆變器等效電路

Fig.4 Equivalent circuit of grid-connected inverter considering PLL

（1）從并網電流2到參考電流ref之間引入一條傳遞函數為X()的支路，此時，ref()=2PLL1()pcc()+X()2()，等效為在并網逆變器輸出端串聯一個阻抗X，以對輸出阻抗進行重塑，如圖4b所示，其中，阻抗X可以通過合理設計傳遞函數X()進行配置。

（2）從并網點電流2到并網點電壓pcc之間引入一條傳遞函數為Y()的支路，等效為在并網逆變器輸出端并聯阻抗Y，以對系統輸出阻抗進行重塑，如圖4c所示，其中，阻抗Y可以通過合理地設計傳遞函數Y()進行配置。

上述兩種方法均可以對輸出阻抗out-PLL進行重塑，提升其在交截頻率范圍內的穩定裕度，從而達到減小甚至消除PLL的影響。結合本文新型PLL的設計方法，為避免引入額外的電流支路或相位補償環節，只考慮方法（1），方法（2）暫不考慮。

2 新型PLL及其參數設計方法

2.1 新型PLL的提出

基于第1節分析，本文提出了一種以并網點電壓、并網點電流為輸入信號的新型PLL設計方法，具體控制結構如圖5所示。圖5中，v()為微分環節，w()為阻抗重塑環節，q()為相位補償環節。

由圖5可以看出，根據輸入信號的不同，新型PLL控制結構可分為兩部分：第一部分為基于并網點電壓pcc()為輸入信號的鎖相功能部分；第二部分為基于并網點電流2()為輸入信號的提高PLL魯棒性部分，這兩部分均為基頻信號輸入。以下分別從新型PLL高魯棒性、阻抗重塑環節和相位矯正環節三個角度進行分析與設計。

2.2 新型PLL高魯棒性分析

本節暫不考慮阻抗重塑環節與相位補償環節。為提高PLL自身魯棒性，降低傳統PLL輸入信號中所含分量g2對PLL自身穩定性的影響，如圖5所示，可采用小信號注入法對電網阻抗進行在線測量[17-18]，即利用電網阻抗測量值g0與微分環節v()對新型PLL中并網電流2()支路進行動態調整，進而實現對傳統PLL輸入信號中所含分量g2的限制。

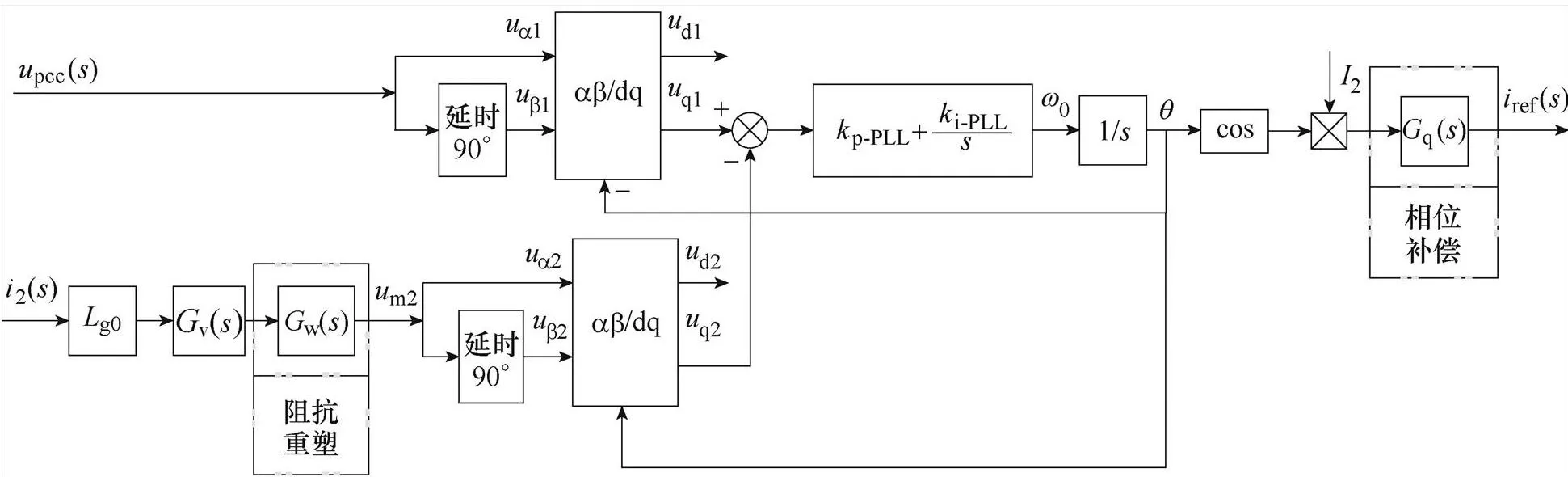
圖5 新型PLL控制結構

由于二階線性微分跟蹤器在實際工程中易于實現，且具有良好的高頻噪聲抑制能力[19]，本文使用二階線性微分跟蹤器代替傳統微分環節v0()=，其中，二階線性微分跟蹤器的表達式v()為

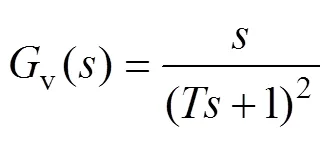
式中，為二階線性微分跟蹤器的時間常數。

圖6給出了二階線性微分跟蹤器v()與傳統微分環節v0()的伯德圖。

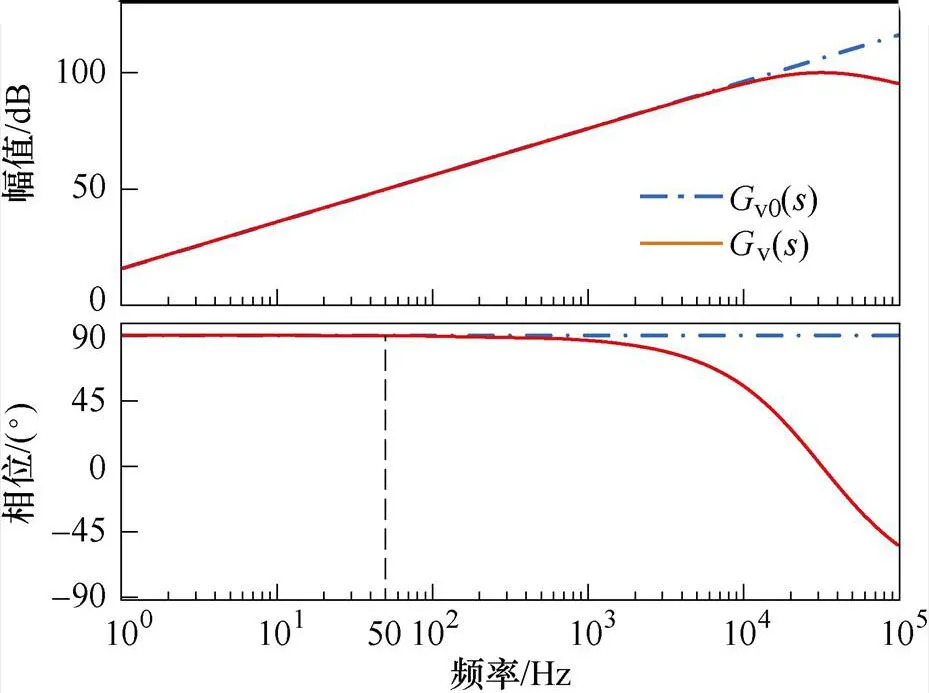
圖6 不同微分環節伯德圖

圖6中，對于時間常數的取值，只需二階線性微分跟蹤器的轉折頻率1/大于系統開關頻率即可，結合表1參數，本文取=5ms。

從圖6中可以看出，二階線性微分跟蹤器與傳統微分環節在低于1 kHz頻率范圍內幾乎重合，雖然高頻處有一定差別，但高頻信號對并網電流2()支路的輸入信號影響很小，可忽略不計。

結合圖5和式（2）可以推導出，新型PLL中參考電流ref()對并網電流2()支路的傳遞函數表達式PLL2()為

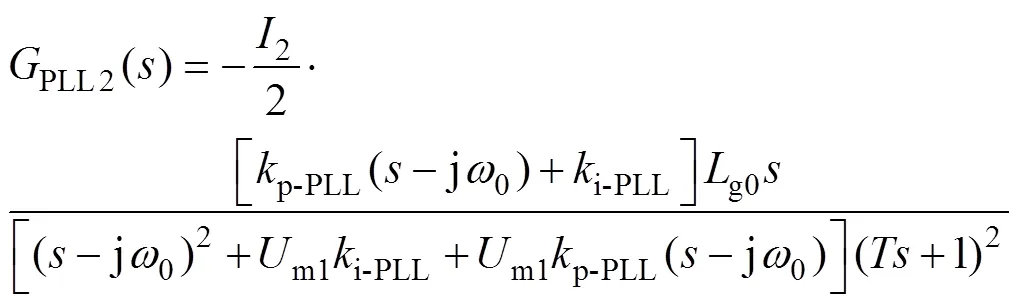
為進一步揭示新型PLL的高魯棒性，根據圖5可得并網電流2()支路中等效電壓m2()和并網電流2()之間的相量關系為

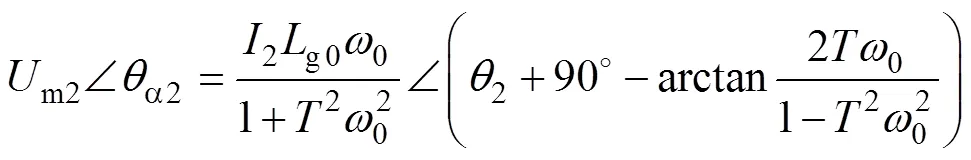
式中，m2、a2為m2()的幅值、相位；g00為在線測量電網阻抗模值。

借鑒式（4）～式（6）的分析方法，對式（14）進行分析與化簡，同時，考慮時間常數的取值，可得簡化后的分量q2為

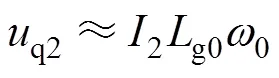
結合式（6）、式（15）和圖2可得新型PLL控制系統框圖，如圖7所示。

根據圖7可得新型PLL輸出相位對參考輸入相位g的閉環傳遞函數表達式2()為

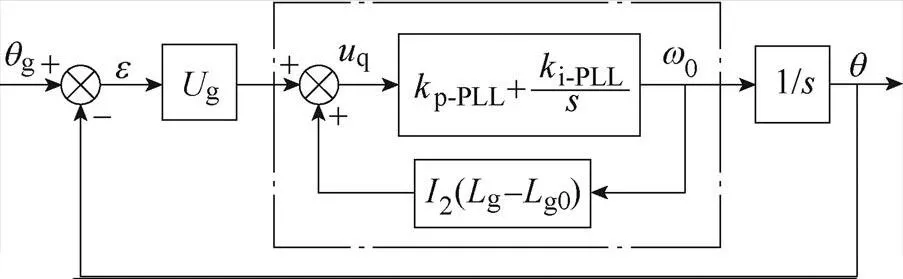
圖7 弱電網下新型PLL控制系統框圖

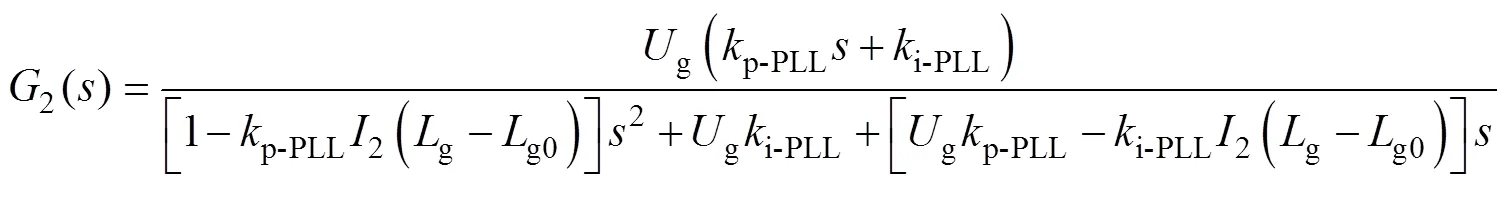
由于g0為在線測量值，具有一定誤差，其誤差范圍通常在±20 %之間，考慮其誤差最大情況即g0=0.8g，若系統在此情況下PLL依舊具有穩定性，則說明g0在誤差范圍內無論取何值，均可以保證PLL穩定運行。結合表1參數并考慮電網阻抗寬范圍變化情況，當電網阻抗g=31.2 mH（SCR=1）時，新型PLL控制系統仍未產生右半平面閉環極點，即PLL系統保持穩定，有效降低了弱電網下傳統PLL輸入信號中所含分量g2對PLL自身穩定性影響。

2.3 阻抗重塑環節分析與設計

在上述分析基礎上，為降低負阻抗PLL對系統穩定性的影響，可在新型PLL中并網點電流2()支路上串聯超前校正器w()，其等效為1.3節所述第（1）種方法，即通過串聯阻抗對系統輸出阻抗out-PLL進行重塑，具體分析與設計過程如下。

對于w()的設計，首先應滿足w()在基頻處的幅值與相位為0，以保證新型PLL的高魯棒性；其次w()環節在交截頻率范圍內應具有較高相位，以提高輸出阻抗out-PLL在交截頻率處的穩定裕度。超前校正器w()的[20]表達式為

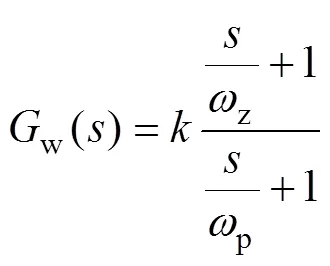
式中，為超前校正器的開環增益。

結合表1參數，系統輸出阻抗out-PLL的交截頻率介于z=100 Hz與p=250 Hz之間時，系統穩定裕度較低，由此可得

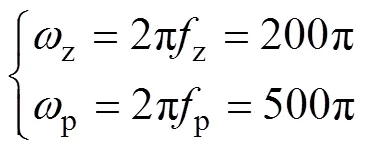
結合式（13）、式（17）和圖5可得不考慮相位補償時，新型PLL中參考電流ref()對并網電流2()支路的傳遞函數ZPLL2()為

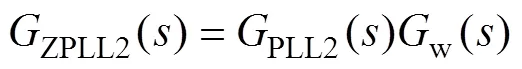
圖8所示為傳遞函數PLL2()和ZPLL2()的伯德圖。對比PLL2()和ZPLL2()可以看出，相較于PLL2()，考慮阻抗重塑時ZPLL2()會在50 Hz基頻處產生很小的相位偏差，但對鎖相功能無影響。此外，ZPLL2()的基頻幅值與w()中的系數有關，出于減小誤差考慮，本文選擇=1，此時基頻幅值無誤差。

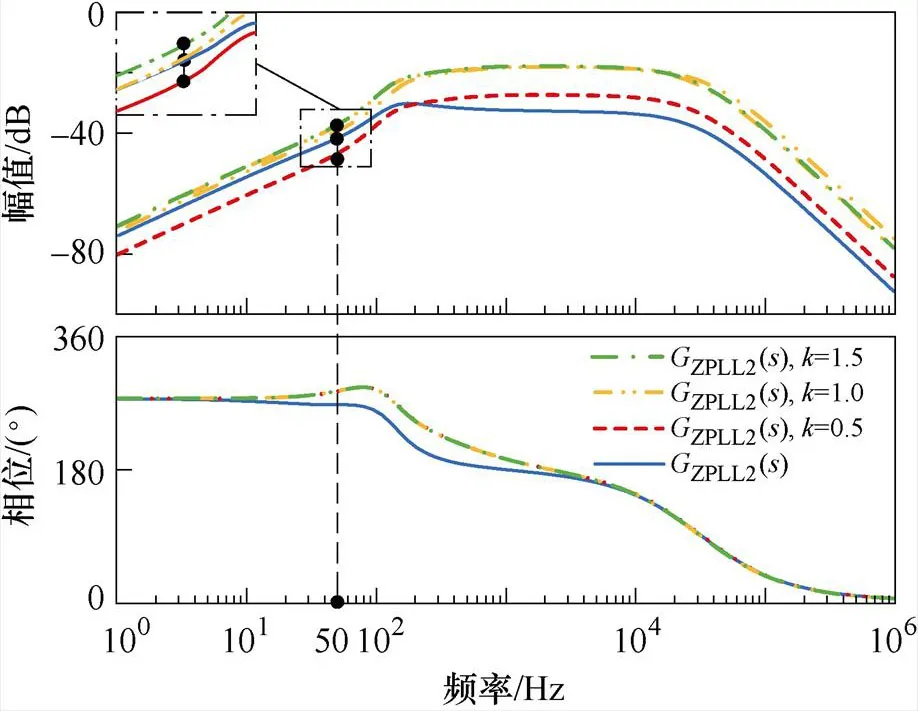
圖8 不同k值下GPLL2(s)、GZPLL2(s)伯德圖

進一步地，結合式（19）與圖5可知，參考電流ref()=2PLL1()pcc()+ZPLL2()2()。將ref()代入式（8）可得，阻抗重塑后的系統輸出阻抗out-ZPLL為

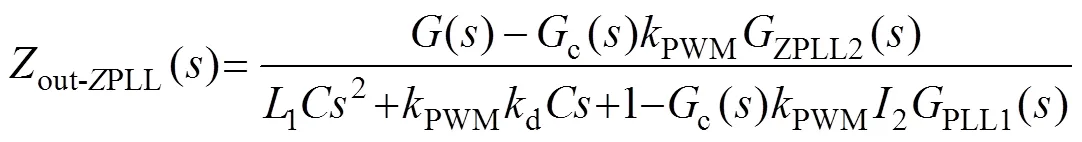
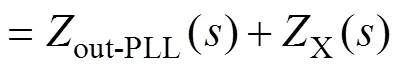
根據圖4b可知，在輸出阻抗支路串聯的阻抗X為

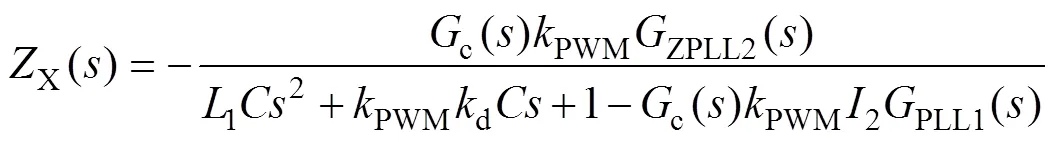
根據式（10）、式（20）、式（21）可以繪制out-PLL、out、X和out-ZPLL的伯德圖，如圖9所示。

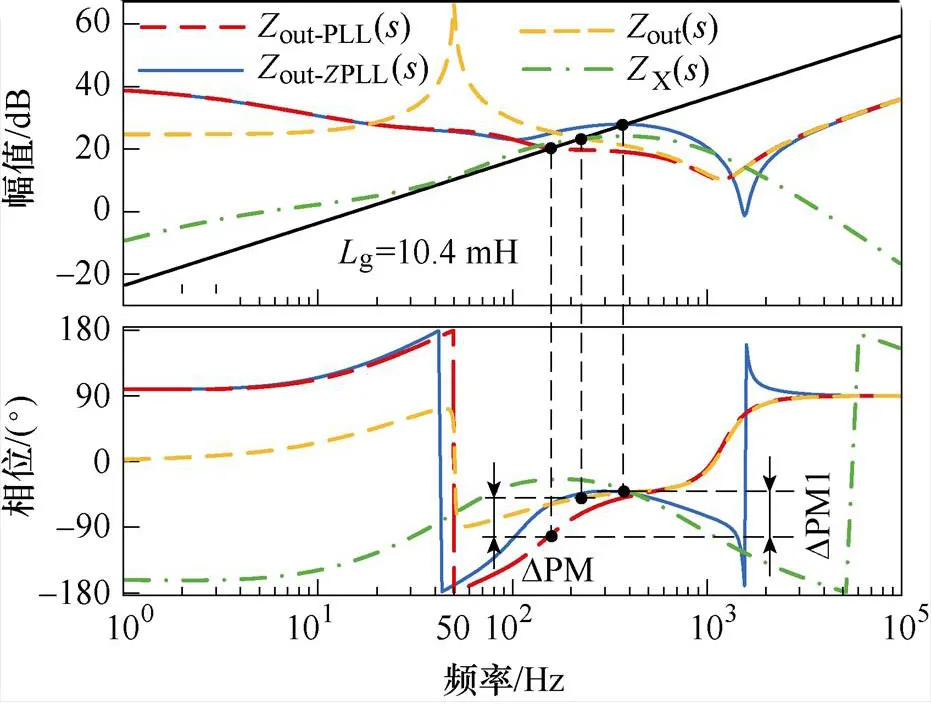
圖9 Zout、Zout-PLL、Zout-ZPLL和ZX的伯德圖

根據式（20）可知重塑后的系統輸出阻抗out-ZPLL是由阻抗X與阻抗out-PLL串聯所得。分析圖9，阻抗X在交截頻率范圍內相位較高，且大于阻抗out-PLL的相位，因此，相較于阻抗out-PLL，阻抗out-ZPLL在交截頻率處的相位大幅提升，且提升角度為DPM1，同時，系統穩定裕度顯著提高，系統魯棒性得到保證。

此外，由于新型PLL控制結構改變了傳統PLL的輸入信號，所以會導致新型PLL的輸出相位與并網點電壓pcc()之間存在相位偏差。從圖9也可以看出，阻抗重塑后的out-ZPLL與阻抗未重塑時的out-PLL在50 Hz基頻處相位不同步，因此需要進行必要的基頻相位矯正。

2.4 相位矯正環節分析與設計

由于逆變器穩定運行時，PCC電壓與電網電壓相位差較小，且與并網電流相位一致，即g-q≈0，2-q=0，進而得出2≈g

根據上述分析，傳統PLL下，式（5）中的q軸信號分量可化簡為信號qc，即

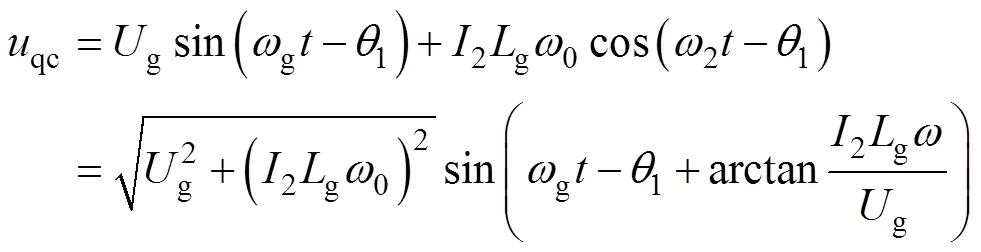
由式（22）可得，傳統PLL輸出的相位1為

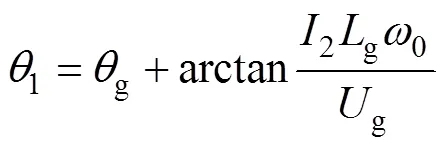
同理，結合式（5）、式（14）、式（15）可得新型PLL下化簡后的q軸信號分量qx為

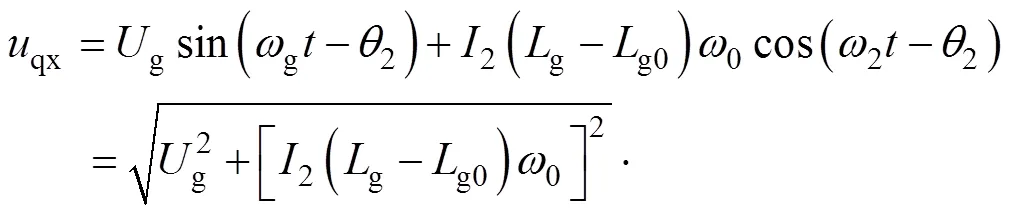
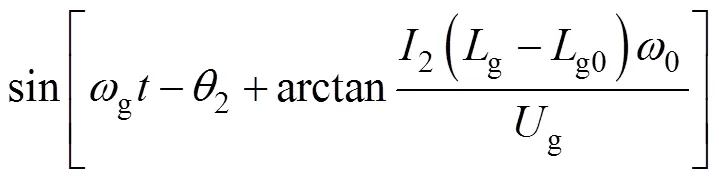
由式（24）可得，新型PLL輸出的相位2為

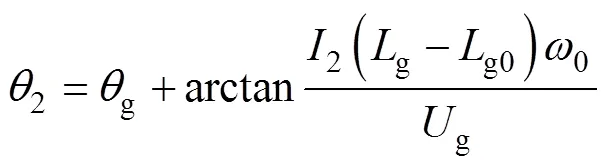
將式（23）與式（25）作差可得，傳統PLL與新型PLL輸出的相位誤差Dq1為

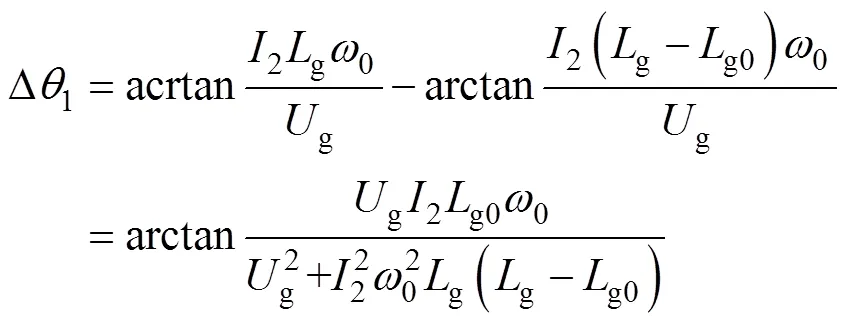
式（26）為新型PLL需要進行相位矯正的相位大小，由于含有未知量電網電感g和電網電壓幅值g，所以使用在線測量信號近似代替未知信號，即g0≈g和pcc≈g，則相位近似矯正1為

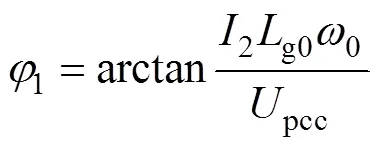
為證明相位近似矯正的可行性，令式（26）與式（27）作差可得相位近似矯正的誤差大小Dq2為

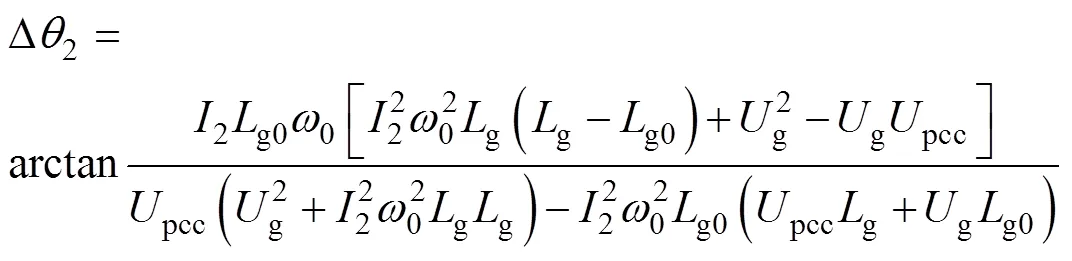
將表1所示參數代入式（28），可得相位近似矯正的誤差數量級為10-3，對于反三角函數而言，可忽略不計，所以相位偏差可按1進行矯正。

為便于在實際工程中進行相位矯正，考慮到全通濾波器只會從轉折頻率處改變相位，并且不會改變原有信號的幅值，因此在新型PLL后串聯一階全通濾波器q()環節用于相位矯正[21]，q()表達式為

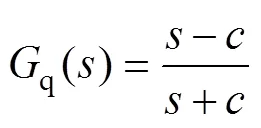
式中，為q()的轉折頻率。

令j0，并代入式（29）中可以推導出全通濾波器q()在基頻處的相位表達式為

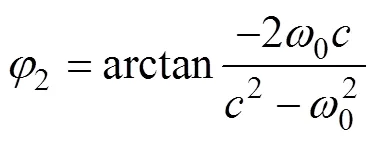
令式（27）與式（30）相等，即1=2。則有

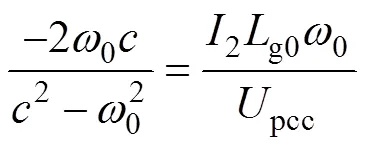
由式（31）即可得到全通濾波器的轉折頻率，進而實現相位矯正。

3 系統魯棒性分析

并網逆變器控制系統的魯棒性可通過推導其輸出阻抗并借助阻抗穩定判據進行分析，鑒于此，本節首先給出了基于新型PLL控制時的系統輸出阻抗與控制框圖，然后通過設計示例從理論層面說明本文所提新型PLL的有效性。

3.1 新型PLL下系統輸出阻抗

當采用圖5所示新型PLL時，考慮式（2）、式（19）、式（29），可得參考電流ref()到并網點電壓pcc()和并網電流2()的函數關系表達式為

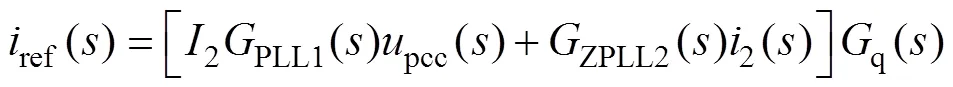
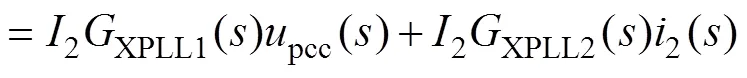
式中，XPLL1()、XPLL2()分別為新型PLL環節中并網點電壓和并網點電流的等效傳遞函數。

根據上述分析可得如圖10所示的基于新型PLL的系統控制框圖。

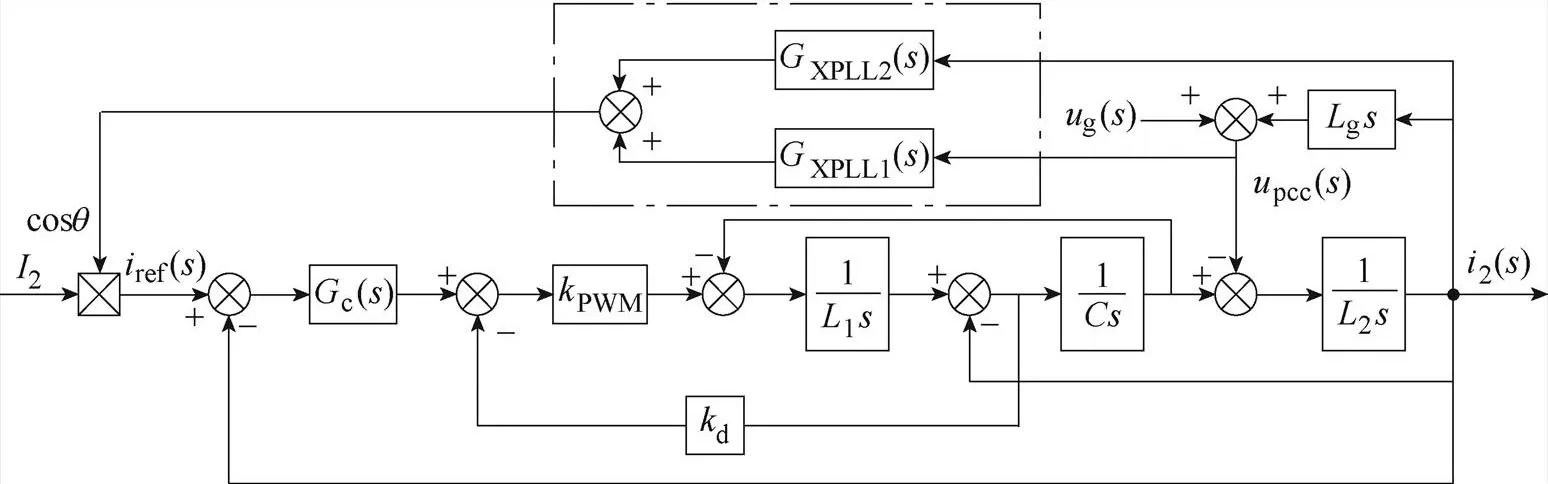
圖10 新型PLL的系統控制框圖

將式（32）代入式（8），可得考慮新型PLL時系統的輸出阻抗out-XPLL()為

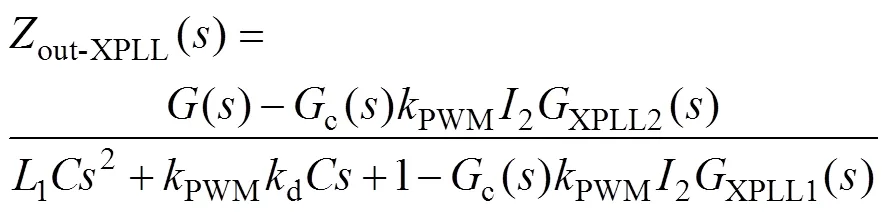
3.2 系統魯棒性分析

為了便于對比分析，給出并網逆變器的相關參數見表1。此外，為了保證PLL具有較好的動態響應能力，本文以PLL帶寬BW=250 Hz為例進行設計[16]。

圖11給出了考慮傳統PLL控制時的系統輸出阻抗out-PLL的伯德圖。從圖中可以看出，采用傳統PLL控制時，隨著電網阻抗g的增大，系統輸出阻抗out-PLL與g在交截頻率范圍內的相位裕度逐漸減小，系統魯棒性逐漸下降直至失穩。

圖12為不同電網阻抗、不同短路比時，新型PLL下有無考慮誤差時的系統輸出阻抗out-XPLL的伯德圖。

由圖12a可知，采用新型PLL控制時，弱電網下，當電網阻抗g=10.4 mH（SCR=3）時，系統相位裕度提升了57.8 °，相位裕度為47.8 °，系統魯棒性得到保證；極弱電網下，即使當電網阻抗g= 20.8 mH（SCR=1.5）或g=31.2 mH（SCR=1）時，系統的相位裕度分別提升了101.3 °、120.4 °，相位裕度分別為54.3 °、58.4 °，系統依舊具有極高的魯棒性。此外，考慮到新型PLL中電網阻抗測量值g0存在一定誤差，且誤差范圍通常在±20 %之間。以SCR=1.5時為例，圖12b給出了考慮誤差時的系統輸出阻抗out-PLL伯德圖。從圖中可以看出，系統相位裕度依然大于50 °，滿足實際工程要求。

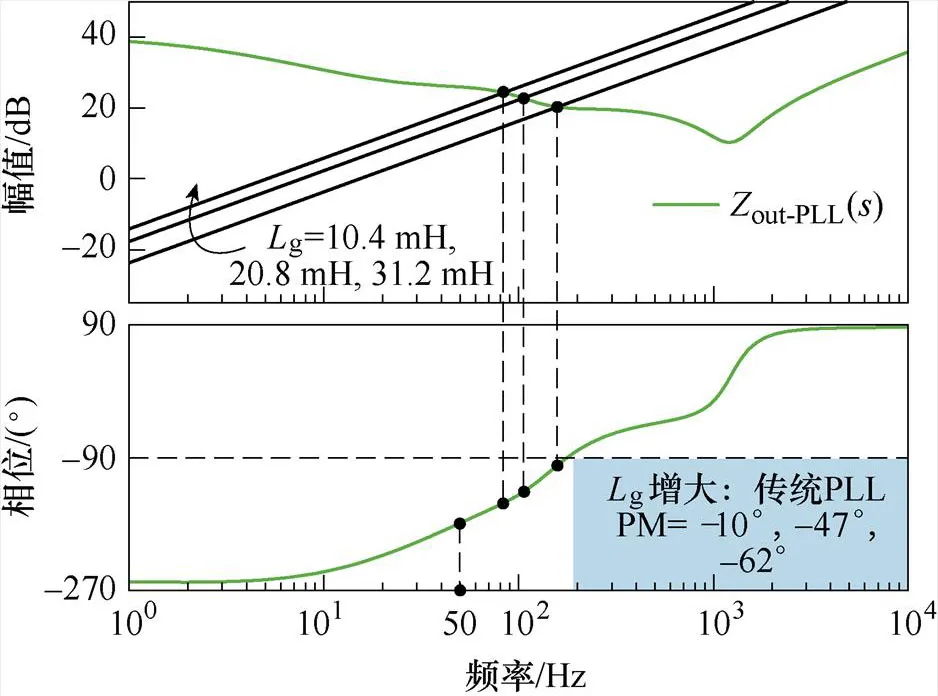
圖11 不同電網阻抗下Zout-PLL的伯德圖

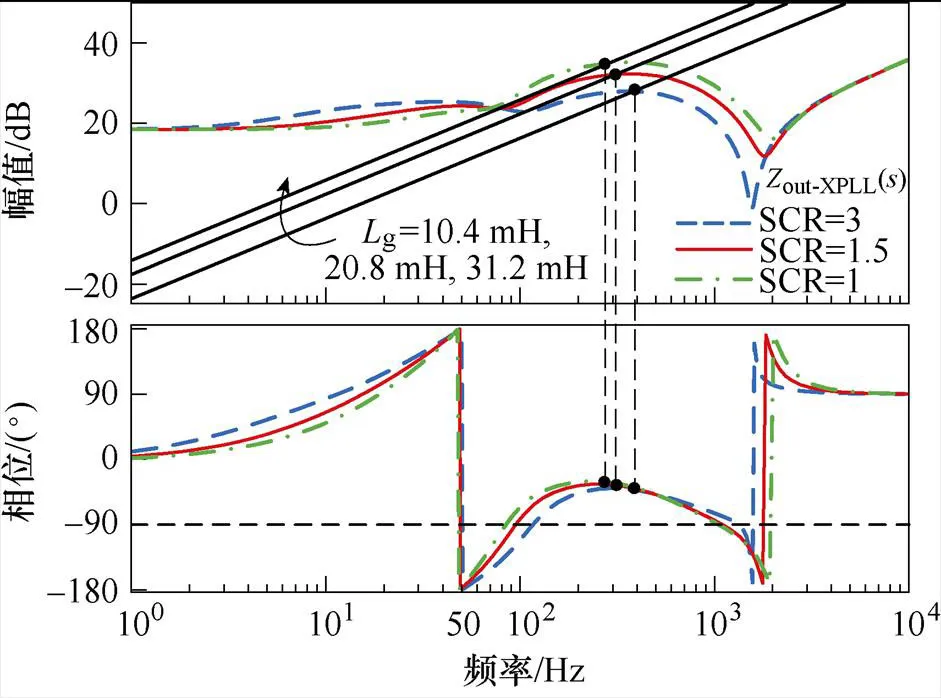
（a）不同電網阻抗下out-XPLL的伯德圖

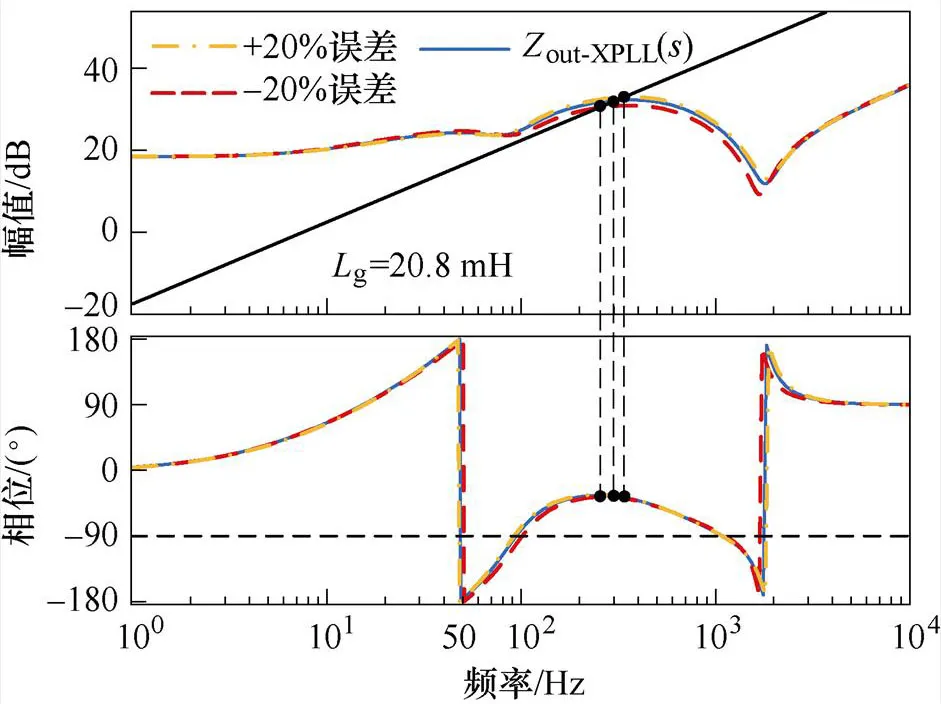
（b）考慮誤差下out-XPLL的伯德圖

圖12out-XPLL的伯德圖

Fig.12 Bode plot ofout-XPLL

4 仿真與實驗驗證

4.1 仿真驗證

為驗證所提新型PLL的有效性，在Matlab/ Simulink中搭建了單相LCL型并網逆變器仿真模型，參數見表1。

圖13為采用傳統PLL和新型PLL控制時的系統仿真波形。采用傳統PLL控制時，如圖13a所示，當電網阻抗g=2.6 mH（SCR=12）時，并網電流波形穩定；當電網阻抗g=5.2 mH（SCR=6）時，并網電流總諧波畸變率（Total Harmonic Distortion, THD）為4.93 %，已處于并網標準的臨界值；當電網阻抗g=10.4 mH（SCR=3）時，并網電流發生嚴重振蕩，且已無法滿足并網要求。采用新型PLL控制時，如圖13b所示，并網電流質量得到了明顯改善，并且在極弱電網下，如電網阻抗g=31.2 mH（SCR=1）時，并網電流THD為1.47 %，依然滿足并網要求。此外，如圖13c所示，采用新型PLL控制時，并網點電壓、電流不存在相位偏差，滿足并網點單位功率因數并網的要求。

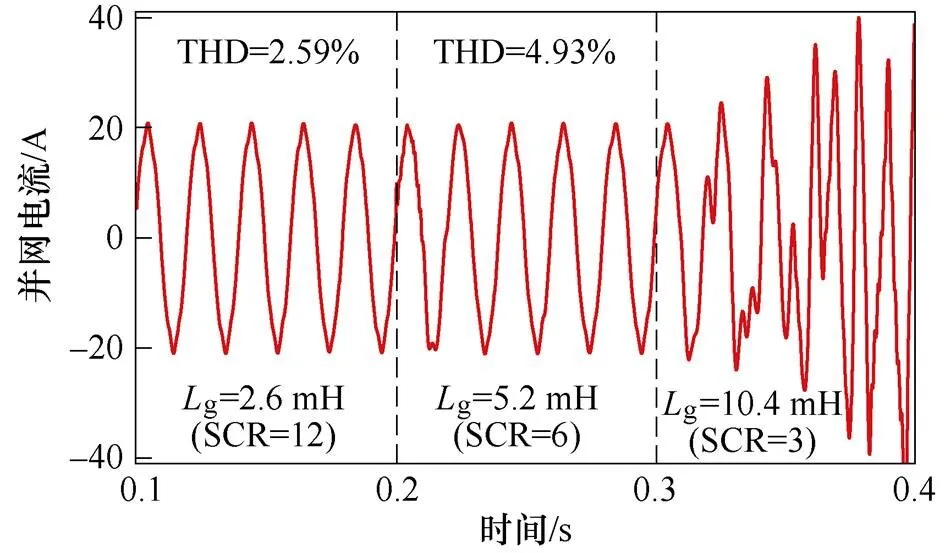
（a）傳統PLL控制時并網電流仿真波形

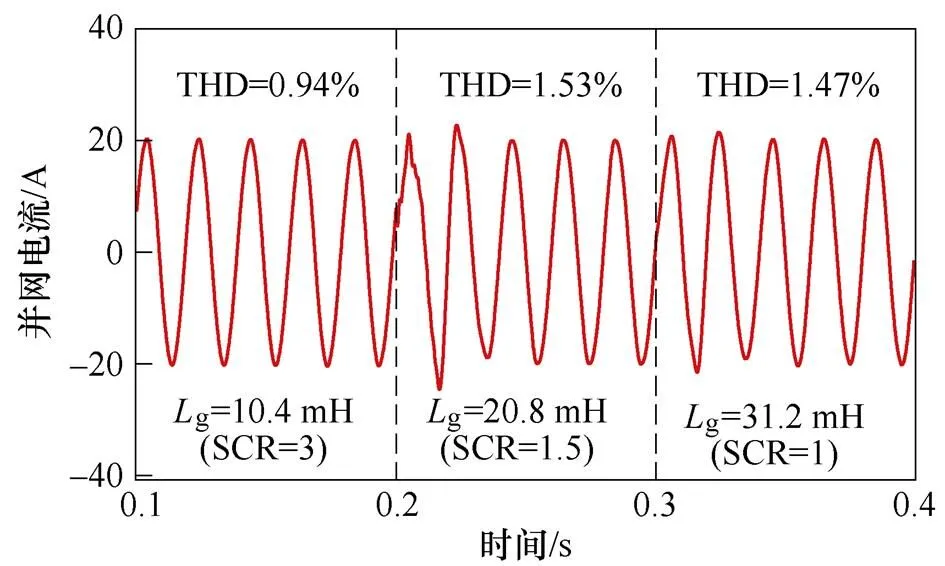
（b）新型PLL控制時并網電流仿真波形

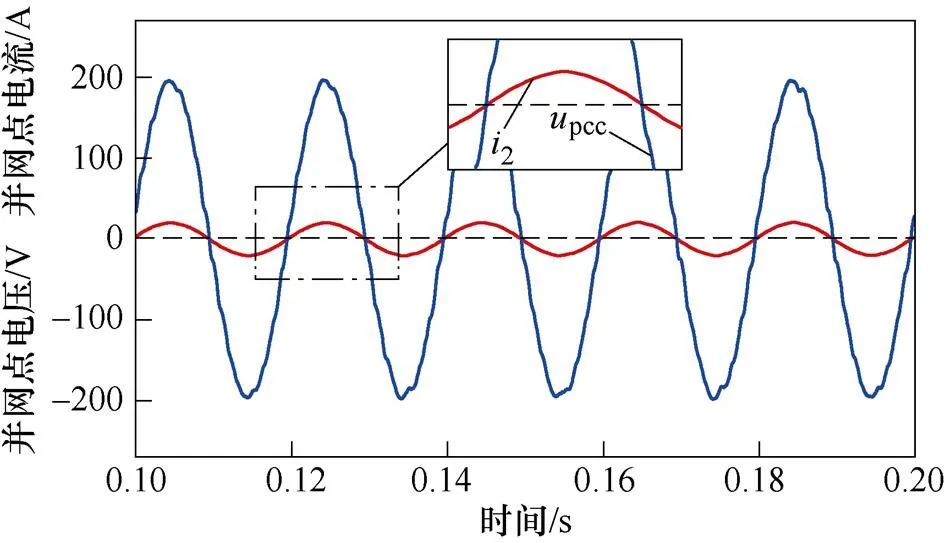
（c）新型PLL控制時并網點電流、電壓仿真波形

圖13 傳統PLL與新型PLL控制時系統仿真波形

Fig.13 System simulation waveforms of traditional PLL and new PLL control

4.2 實驗驗證

為進一步驗證本文所提新型PLL的有效性，采用實時數字控制器RTU-BOX204控制平臺，搭建了如圖14所示的2 kW單相LCL型并網逆變器實驗平臺，具體實驗參數與表1一致。

圖15為采用傳統PLL控制時并網點電壓、電流實驗波形。從圖15可以看出，當電網阻抗g= 5.2 mH時，并網電流出現較大畸變，當g繼續增大時，并網電流會出現嚴重畸變甚至發生振蕩，實驗樣機自動保護，系統斷開。

圖16為采用新型PLL控制時的系統并網點電壓、電流實驗波形。從圖中可以看出，當電網阻抗g=10.4 mH（SCR=3）和g=20.8 mH（SCR=1.5）時，并網電流保持穩定運行，系統魯棒性得到加強；當電網阻抗g=31.2 mH（SCR=1）時，并網電流仍能穩定運行且畸變較小。并且并網電壓與并網電流同時過零點，無相位偏差。以上實驗結論與4.1節仿真驗證結論一致，但是需要指出的是，由于電網阻抗的存在，并網點電壓不可避免地受到影響，并且隨著電網阻抗g的增大，并網電壓出現了明顯的低頻諧波失真，同時，電網電壓的相位與并網點電壓相位偏差的逐漸增大，導致并網點電壓幅值下降。

圖14 實驗平臺示意圖

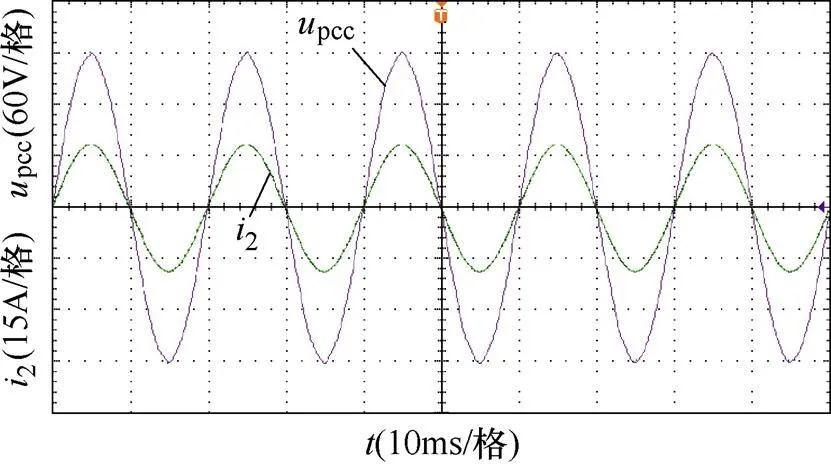
（a）g=10.4 mH

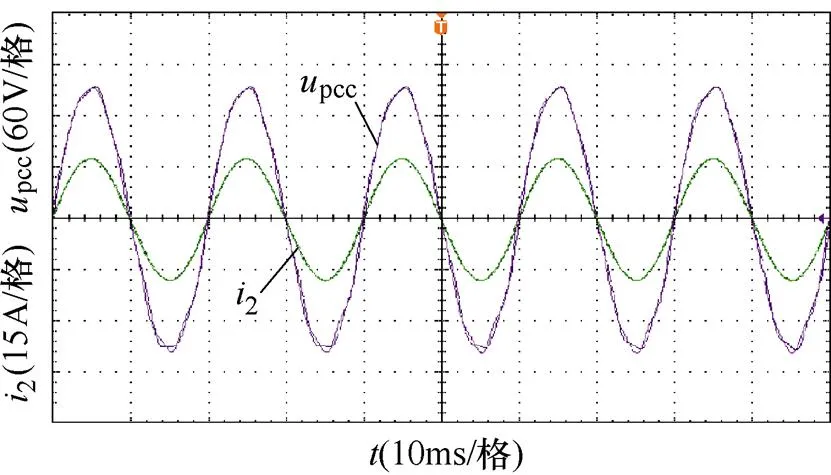
（b）g=20.8 mH

（c）g=31.2 mH

圖16 新型PLL控制時并網點電壓、電流波形

Fig.16 Experimental waveforms of voltage and current under new PLL control

此外，圖17給出了新型PLL控制時系統并網電流跳變時的動態實驗波形，為使動態實驗波形更加清晰直觀，此實驗選擇在電網阻抗g=5.2 mH的情況下進行，此時并網點電壓、電流畸變率均較小。如圖17所示，當實驗設置參考電流由滿載到半載跳變時，并網電流在跳變瞬間出現短暫的調節過程，并在半個工頻周期內進入穩態，說明基于新型PLL控制時系統具有良好的動態性能。

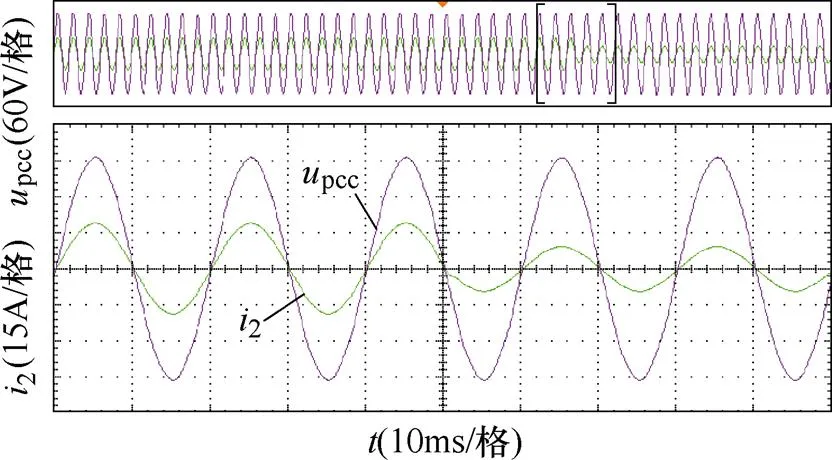
圖17 新型PLL控制時并網點電壓、電流動態實驗波形

基于上述仿真與實驗結果表明，提出的新型PLL控制結構可以有效解決高滲透率下系統魯棒性下降甚至失穩問題，拓寬了弱電網甚至極弱電網下系統對電網阻抗寬范圍變化的適應能力。

5 結論

本文以LCL濾波單相并網逆變器為例，提出了一種新型PLL控制結構，該結構能夠有效解決高滲透率下PLL與系統魯棒性下降問題，并得到以下幾點結論：

1）高滲透率下，PLL與電網阻抗之間存在耦合，等效為在PLL控制環路中引入了一條與電網阻抗有關的正反饋回路，此反饋回路直接影響了PLL輸出及其自身穩定性。

2）從阻抗角度分析，PLL的引入降低了并網逆變器輸出阻抗的相位，并且系統的交截頻率隨著電網阻抗的增大而減小，二者共同作用導致系統穩定裕度降低甚至系統失穩。

3）所提新型PLL控制結構通過對系統輸出阻抗進行重塑和相位校正，即使是在極弱電網下，依舊可以準確提取電壓相位并確保系統高魯棒性，拓寬了高滲透率下并網逆變器電流控制系統對電網阻抗的適應范圍。

4）下一步將在本文1.3節所提串并聯阻抗重塑的基礎上，通過對并網逆變器控制框圖的等效變換，推導得到可以完全消除負阻抗PLL對輸出阻抗影響的電網電壓前饋函數，并基于電網電壓前饋控制實現對逆變器輸出阻抗相位特性進行重塑。

[1] 沈姝衡, 方天治, 章益凡. 高帶寬數字控制LCL型并網逆變器及其提高并網系統魯棒性的諧振抑制技術研究[J]. 電工技術學報, 2022, 37(21): 5548- 5561.

Shen Shuheng, Fang Tianzhi, Zhang Yifan. A high- bandwidth digital-control LCL-type grid-tied inverter and resonance-suppressing technique for improving the robustness of grid-connected system[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(21): 5548-5561.

[2] Wang Xiongfei, Blaabjerg F, Loh P C. Grid-current- feedback active damping for LCL resonance in grid- connected voltage-source converters[J]. IEEE Transa- ctions on Power Electronics, 2016, 31(1): 213-223.

[3] 李明. 高滲透率新能源發電并網逆變器阻抗自適應雙模式控制研究[D]. 合肥: 合肥工業大學, 2020.

[4] 郭小強, 朱鐵影. 新型非隔離型三相三電平光伏并網逆變器及其漏電流抑制研究[J]. 電工技術學報, 2018, 33(1): 26-37.

Guo Xiaoqiang, Zhu Tieying. Research on leakage current suppression of novel three-phase three-level non-isolated PV inverter[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 26-37.

[5] Davari M, Mohamed Y A R I. Robust vector control of a very weak-grid-connected voltage-source converter considering the phase-locked loop dynamics[J]. IEEE Transactions on Power Electronics, 2017, 32(2): 977- 994.

[6] 張興, 李明, 郭梓暄, 等. 新能源并網逆變器控制策略研究綜述與展望[J]. 全球能源互聯網, 2021, 4(5): 506-515.

Zhang Xing, Li Ming, Guo Zixuan, et al. Review and perspectives on control strategies for renewable energy grid-connected inverters[J]. Journal of Global Energy Interconnection, 2021, 4(5): 506-515.

[7] 許津銘, 卞申一陽, 錢浩, 等. 弱電網下單相并網逆變器延時鎖相環的魯棒控制及優化方法[J]. 中國電機工程學報, 2020, 40(7): 2062-2070, 2386.

Xu Jinming, Bian Shenyiyang, Qian Hao, et al. Robust control and optimization of delay-based phase-locked loop of single-phase grid-connected inverters under weak grid conditions[J]. Proceedings of the CSEE, 2020, 40(7): 2062-2070, 2386.

[8] 涂春鳴, 高家元, 李慶, 等. 具有復數濾波器結構鎖相環的并網逆變器對弱電網的適應性研究[J]. 電工技術學報, 2020, 35(12): 2632-2642.

Tu Chunming, Gao Jiayuan, Li Qing, et al. Research on adaptability of grid-connected inverter with com- plex coefficient-filter structure phase locked loop to weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(12): 2632-2642.

[9] Cespedes M, Sun Jian. Adaptive control of grid- connected inverters based on online grid impedance measurements[J]. IEEE Transactions on Sustainable Energy, 2014, 5(2): 516-523.

[10] 許津銘, 謝少軍, 唐婷. 弱電網下LCL濾波并網逆變器自適應電流控制[J]. 中國電機工程學報, 2014, 34(24): 4031-4039.

Xu Jinming, Xie Shaojun, Tang Ting. An adaptive current control for grid-connected LCL-filtered inver- ters in weak grid case[J]. Proceedings of the CSEE, 2014, 34(24): 4031-4039.

[11] 錢一濤, 趙晉斌, 馬俊清, 等. 弱電網基于對稱PLL結構的并網逆變器頻率耦合消除與穩定性增強方法[J]. 電網技術, 2022, 46(10): 3893-3901.

Qian Yitao, Zhao Jinbin, Ma Junqing, et al. Gird- connected inverter frequency coupling elimination and stability enhancement method based on sym- metrical PLL structure under weak grid[J]. Power System Technology, 2021, 46(10): 3893-3901.

[12] Yang Dongsheng, Wang Xiongfei, Liu Fangcheng, et al. Symmetrical PLL for SISO impedance modeling and enhanced stability in weak grids[J]. IEEE Transa- ctions on Power Electronics, 2019, 35(2): 1473-1483.

[13] 杜燕, 言明明, 楊向真, 等. 多目標約束下逆變器阻抗的電流矯正方法[J]. 控制理論與應用, 2022, 39(4): 701-710.

Du Yan, Yan Mingming, Yang Xiangzhen, et al. Current correction method for grid-connected inverter impedance under multi-objective constraints[J]. Con- trol Theory & Applications, 2022, 39(4): 701-710.

[14] 高家元, 肖凡, 姜飛, 等. 弱電網下具有新型PLL結構的并網逆變器阻抗相位重塑控制[J]. 中國電機工程學報, 2020, 40(20): 6682-6694.

Gao Jiayuan, Xiao Fan, Jiang Fei, et al. Grid- connected inverter impedance phase reshaping control with novel PLL structure in weak grid[J]. Proceedings of the CSEE, 2020, 40(20): 6682-6694.

[15] 張燁, 田慕琴, 宋建成, 等. 弱電網下計及鎖相環影響的并網逆變器輸出阻抗重塑[J]. 高電壓技術, 2021, 47(11): 4033-4044.

Zhang Ye, Tian Muqin, Song Jiancheng, et al. Recon- struction of the output impedance of grid-connected inverter considering PLL effect in weak grids[J]. High Voltage Engineering, 2021, 47(11): 4033-4044.

[16] 吳恒, 阮新波, 楊東升. 弱電網條件下鎖相環對LCL型并網逆變器穩定性的影響研究及鎖相環參數設計[J]. 中國電機工程學報, 2014, 34(30): 5259- 5268.

Wu Heng, Ruan Xinbo, Yang Dongsheng. Research on the stability caused by phase-locked loop for LCL- type grid-connected inverter in weak grid condition[J]. Proceedings of the CSEE, 2014, 34(30): 5259-5268.

[17] 涂春鳴, 高家元, 趙晉斌, 等. 弱電網下具有定穩定裕度的并網逆變器阻抗重塑分析與設計[J]. 電工技術學報, 2020, 35(6): 1327-1335.

Tu Chunming, Gao Jiayuan, Zhao Jinbin, et al. Analysis and design of grid-connected inverter impedance remodeling with fixed stability margin in weak grid[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1327-1335.

[18] 李楊, 帥智康, 方俊彬, 等. 基于阻抗測量的多逆變器系統穩定性校驗方法[J]. 電力系統自動化, 2021, 45(11): 95-101.

Li Yang, Shuai Zhikang, Fang Junbin, et al. Stability check method for multi-inverter system based on impedance measurement[J]. Automation of Electric Power Systems, 2021, 45(11): 95-101.

[19] 鄧吉鴿. 高階線性跟蹤微分器性能研究[J]. 艦船電子工程, 2012, 32(4): 68-70.

Deng Jige. Study on high order linear tarcking differentlator[J]. Ship Electronic Engineering, 2012, 32(4): 68-70.

[20] 方天治, 黃淳, 陳乃銘, 等. 一種提高弱電網下LCL型并網逆變器魯棒性的相位超前補償策略[J]. 電工技術學報, 2018, 33(20): 4813-4822.

Fang Tianzhi, Huang Chun, Chen Naiming, et al. A phase-lead compensation strategy on enhancing robustness of LCL-type grid-tied inverters under weak grid conditions[J]. Transactions of China Elec- trotechnical Society, 2018, 33(20): 4813-4822.

[21] 張莉華. 全通IIR數字濾波器的設計和應用[D]. 杭州: 杭州電子科技大學, 2015.

A Phase-Locked Loop Design Method Based on Impedance Remodeling of Grid-Connected Inverter under High Permeability

（Henan Key Laboratory of Intelligent Detection and Control of Coal Mine Equipment School of Electrical Engineering and Automation Henan Polytechnic University Jiaozuo 454003 China）

Under high permeability, the phase-locked loop (PLL), grid impedance, and grid-connected inverter are coupled, seriously impacting the stable operation of the grid-connected inverter system based on synchronous control of PLL. Firstly, for the PLL control structure, grid impedance leads to the introduction of additional feedback loops in the PLL structure. When the grid impedance changes in a wide range, the PLL system will generate the right half plane pole, decreasing the stability of the PLL or even instability. Secondly, for the grid-connected inverter system, when PLL is considered, the additional negative impedance will be introduced into the output impedance of the system, which directly affects the amplitude and phase of the output impedance of the system, decreasing the stability margin of the grid-connected inverter system.

Therefore, this paper takes the single-phase LCL filter grid-connected inverter under the weak current network as the research object and proposes a new PLL control structure with the dot connection current and dot connection voltage as input signals. The new PLL control structure uses the grid impedance measurement value and differential link to dynamically adjust the grid-connected current branch in the new PLL, limiting the grid impedance component in the PLL input signal. Meanwhile, the advance corrector is used to reshape the phase characteristics of the system output impedance. The influence of additional negative impedance on system stability was reduced. Then, the output phase Angle of the new PLL was corrected using an all-pass filter to ensure that the fundamental frequency phase was consistent before and after impedance remodeling.

The robustness analysis of the grid-connected inverter system based on the new PLL control shows that the new PLL structure has high robustness and can reshape the output impedance of the inverter system to improve the phase angle of the output impedance at the intercept frequency. When the system is in a weak grid, the phase margin is greater than 30o, and the system robustness is guaranteed. In addition, the simulation and experimental verification show that the quality of the grid-connected current of the system is improved when the new PLL control is adopted. The voltage and current of the grid connection point do not have phase deviation, which meets the requirements of the grid connection point unit power factor. Moreover, the system has good dynamic performance, and effectively expands the adaptive range of the grid-connected inverter electrical system to the grid impedance under high permeability.

In the next step, the grid voltage feedforward function, which can eliminate the influence of PLL, will be obtained by an equivalent transformation of the control block diagram of the grid-connected inverter. The phase characteristics of the output impedance of the inverter will be reshaped using grid voltage feedforward control to improve the stability of the grid-connected inverter system under high permeability.

High permeability, grid-connected inverters, phase-locked loop, impedance remodeling, robustness

TM464

10.19595/j.cnki.1000-6753.tces.222018

國家自然科學基金資助項目（U1804143）。

2022-10-26

2023-01-08

楊 明 男，1982年生，博士，副教授，研究方向為新能源并網發電技術、電能質量控制、虛擬同步發電機等。E-mail: yangming0391@163.com

楊 倬 男，1999年生，碩士研究生，研究方向為并網逆變器控制及穩定性分析。E-mail: 1135229637@qq.com（通信作者）

（編輯 陳 誠）