中國外商直接投資的空間分異與動態演進
——基于非參數核密度估計的實證研究

裴艷麗，趙 龍

（揚州大學 廣陵學院，江蘇 揚州 225000）

一、引言

改革開放40 多年來，外商直接投資在中國經濟高質量發展中發揮了重要作用，高度流動性的外商直接投資促進我國產業結構轉型升級，也為我國跨國公司核心競爭力的提升創造了條件。但外商直接投資呈現區位分布不均衡、結構分布不合理等特征，制約了地區經濟協同發展。不少學者都對FDI的空間分布特征進行研究，但應用經濟學在研究過程中經常會遇到一個普遍存在的問題，即研究人員在面對大數據時經常需要弄清楚不同研究對象的實際分布特征，對現行經濟數據通過校準隨機模型參數進行準確描述，對未來趨勢發展進行準確預測。

對FDI 分布特征的研究大多從其區位影響因素著手，分析傳統因素和新經濟因素在FDI 區位選擇中分別發揮的作用。Coughlin 等（1991）[1]以美國各州外商直接投資的區位分布實際數值為準探究發展潛力、聚集水平、投資能力對區位選擇的影響。Haskcl 等（2007）[2]認為外商直接投資的區位分布會影響本地區和相鄰地區的經濟效率。Judson 和Owen（1999）[3]構建計量經濟模型，最終發現通貨膨脹率和GDP 水平對區位選擇的影響是顯著的，政府政策的加持加大了其顯著性的體現。Adhikary（2017）[4]基于最小二乘法對南亞國家區位因素進行分析，不同國家呈現出不同的分布特征，利率、匯率、通貨膨脹率等因素對南亞國家區位分布影響呈現不一樣的表現。顏銀根（2014）[5]運用Tobit 面板模型提出同源國效應作為一種新經濟因素對中國外商直接投資的區位選擇產生重大影響。李建華（2019）[6]分析外商直接投資的區位和產業特征，發現產業集聚與外商直接投資呈相輔相成的關系，產業溢出效應與效益效應并存。除此之外，不少國內外學者也從空間視角探究外商在華投資的特征和區位現狀，2000 年Coughlin 最早將計量經濟學方法與研究外商直接投資特征相聯系，發現從空間視角上，本地區FDI 與相鄰地區FDI 呈正相關關系。董玉琪（2018）[7]對江蘇省外商直接投資分布特征分析發現，地區集聚會向周邊城市擴散，二次聚集現象明顯。綜合目前國內外研究結果，在促進國內國際雙循環大背景下，充分把握目前外商直接投資分布特征和動態演化規律對正確制定“引進來”與“走出去”戰略有重要意義。但目前準確描述外商直接投資的分布特征，以數學模型準確描述其分布的實踐較少。因此本文提出一種基于Golub-Welsch 算法的非參數校準方法，以2000—2020 年中國29 個省份面板數據為樣本，考察不同省份的外商直接投資分布特征和動態演進。

二、研究方法和數據

（一）研究方法

核密度估計是一種估計隨機變量的概率密度函數的非參數方法，如果一組數據的密度函數很難基于參數分布估計，采用非參數核密度估計的方式可以較好地描述隨機變量的分布規律。具體的表達公式為：

其中xi是指每一個樣本變量的觀測值，x為均值，K（x）為核函數，要根據不同的樣本類型選擇合適的核函數。h代表帶寬，始終是大于0 的常數。h的取值參照經驗公式：

核密度估計的重點在于核函數和最優帶寬的計算，目前常用的是高斯核函數，Tauchen（1986）[8]，Tauchen 和Hussey（1991）[9]運用有限狀態馬爾科夫鏈方法用于離散具有高斯沖擊的隨機過程。高斯分布模型由于對其分析可處理性較強，一直受到學術界歡迎。姜楠和周曉滄（2006）[10]用非線性規劃的方式改進FCM 算法的不足。劉君（2012）[11]基于多元q-高斯分布研究投資組合模型。夏利宇等（2019）[12]提出基于ACACM 準則的數據離散化算法，用于研究信用評級模型，基于該算法可以提高模型參數準確性和風險控制力。上述研究都是基于高斯分布進行的研究，主要得益于基于高斯分布分析的可處理性較強。但隨著現代經濟的發展，在經濟學中研究非高斯模型正變得越來越普遍。Rietz（1988）[13]將罕見災害的出現引入資產定價模型中，一定程度上解釋了低無風險利率之謎。宮曉莉等（2020）[14]假設信息隨機因子服從非高斯分布，研究B-S 期權定價模型，非高斯分布可以更加準確地描述金融數據的特征。但本文在研究外商直接投資實際數據時，并沒有具體的數學表達式，數據分布較為隨機，基于高斯分布擬合的曲線和實際分布曲線差距較大。唐偉敏等（2020）[15]考慮了一般非高斯馬爾可夫過程的離散化。在其中一種應用中，他們通過用正態混合近似來離散預先指定網格上的非參數密度。因此本文提出一種基于特征值的非參數估計方法，對特征多項式構造三項遞推關系，從而將高斯節點的求解轉變為三項式特征值的求解，用來進行核密度估計和帶寬的計算，并選用一組隨機數值驗證算法的效性，因此本文所提出的方法更容易實現，速度更快。

（二）外商直接投資數據說明

本文所使用數據為2000—2020 年中國各省份的外商直接投資數據，因為西藏和新疆部分數據缺失，因此選用中國29 個省（市、區）的數據。為了對比方便，選擇5 年為一個間隔點，分析2000 年、2005年、2010 年、2015 年、2020 年這5 個年份的外商直接投資動態演進過程，具體數據如表1 所示。

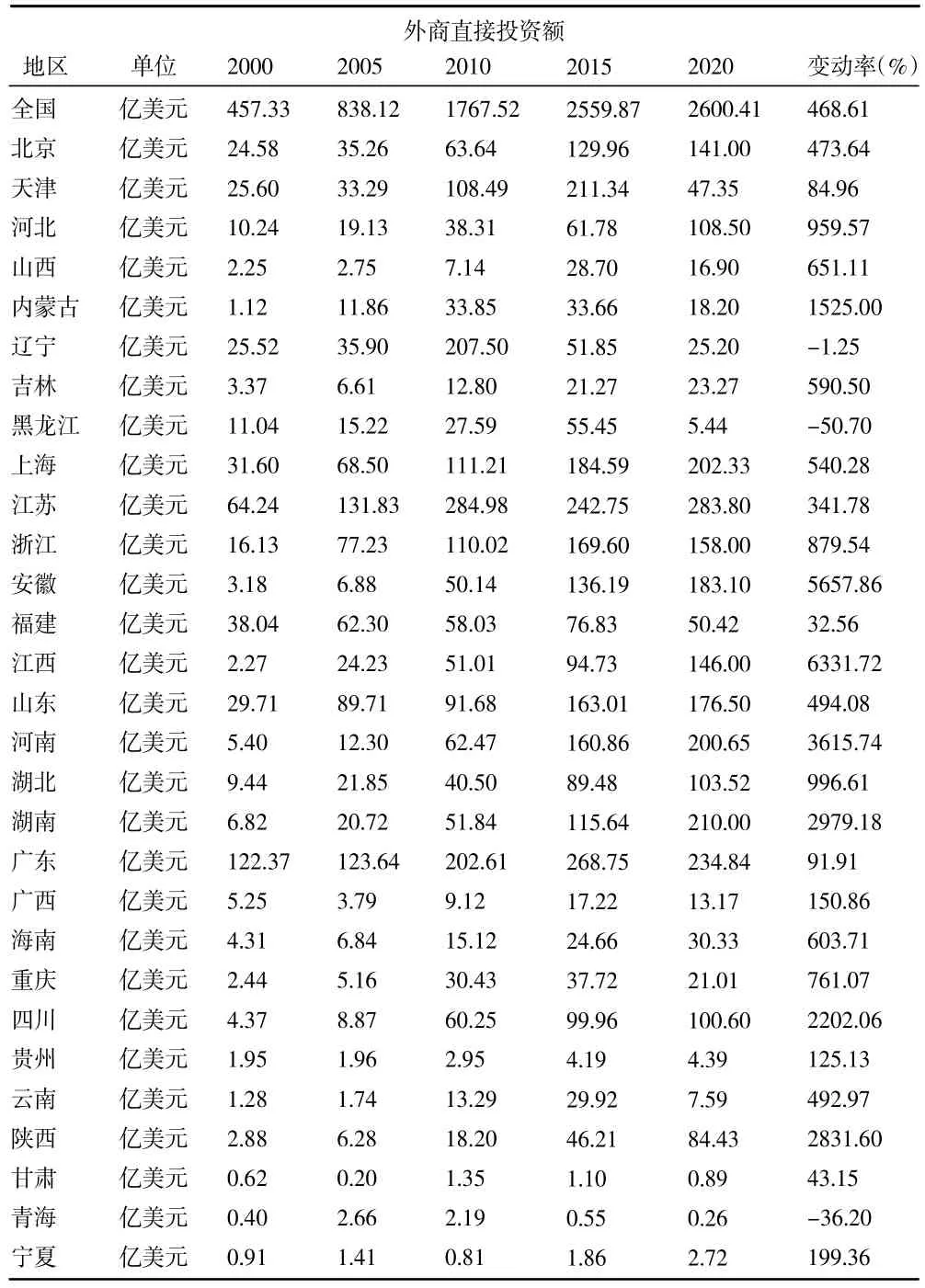
表1 外商直接投資數據

表2 算法1 具體操作步驟

表3 算法2 具體操作步驟

就2020 年而言，外商直接投資總量排名前5 位的省市分別為江蘇、廣東、湖南、上海、河南，直接利用外商直接投資額分別為：283.80 億元、234.84 億元、210.00 億元、202.33 億元、200.65 億元。2015 年，外商直接投資利用額排名前5 位的省市從高到低分別是廣東、江蘇、天津、上海、浙江，利用外商直接投資額分別為：268.75 億元、242.75 億元、211.34 億元、184.59 億元、169.60 億元。近5 年來江蘇、廣東、上海三個省市利用外商直接投資額較為平穩，一直維持在全國前五的地位。從總體狀況看，2000—2020 年各省份利用外商直接投資額呈現增長的態勢，但各個省市利用外商直接投資額的絕對值波動較大。相較于2000 年，只有青海、黑龍江和遼寧三個省份直接外商投資額下降，其余所有省份均上升，增長率排名前5 的省份為江西、安徽、河南、湖南、陜西，江西增長率高達6 331.72%。

三、非參數估計算法的提出

假設非參數密度f（x）已知。由于隨機模型通常涉及期望，因此希望找到節點和權重，使得：

其中g 是被積函數，X 是概率密度為f（x）的隨機變量。等式（1）的右側定義了一個N點求積公式。在此我們假設對于所有的n≥0 存在，其中-∞≤a＜b≤∞是固定的。通過下式定義函數f，g的內積＜f，g＞：

（1）deg（pn）=n且pn的首系數為1；

（2）對于所有的m≠n，有＜pm，pn＞=0。

令a＜x1＜…＜xN＜b是N階正交多項式pN（x）的N個根，并且定義：

是N-1 階多項式，xn取值1，xm（m∈{1，…，N} ）取值為0。則對于所有高達2N-1 階的所有多項式p（x），有：

注意，算法1 的唯一輸入是節點數N和概率密度f的矩，其中k=0，…，2N。因此，對于給定數據的非參數密度離散化，一個自然的想法是將樣本矩輸入到算法1 中。之后基于算法1，構建了以下基于數據的非參數分布自動離散化算法。

由于N點高斯求積具有2N-1 的精度，通過構造N點離散化將數據的樣本矩匹配到2N-1 階（以及數值誤差）。由高斯-馬爾可夫定理可知，樣本矩是總體矩的最佳線性無偏估計，即在形式的所有估計中，具有最小的均方誤差，其中為某個權值，算法2 在某種意義上是最優的，對于在0鄰域內具有有限矩生成函數的隨機變量，分布與其矩生成函數之間存在一一對應關系。因此，應用泰勒近似，我們期望通過匹配足夠多的矩來近似隨機變量的特性。

四、數值仿真分析

（一）精確性分析

與任何數值方法一樣，進行算法的精度評價是非常重要的。由于提出的方法是為了離散非參數分布（特別是非正態分布），因此本文第一個實驗中假設數據分布是正態混合。在第二個實驗中假設數據分布形式是正態分布，以觀察非參數高斯求積方法相對于正確指定參數的方法在性能上有何差異。

1.正態混合分布。為了進行研究，本文設計如下數值實驗。首先，隨機構建一個包含兩個組成部分的正態分布的數據集。各組的比例、均值和標準差分別為p=（pj）=（0.1392，0.8608）、μ=（μi）=（0.15，0.55）和σ=（σj）=（0.05，0.15）。然后根據此概率分布密度生成一組包含5 000 個點的離散數據集。之后，基于生成的離散數據集，采用三種方法分析此數據滿足的概率分布情況。最后，與實際概率分布曲線進行對比，以驗證算法的有效性。這三種方法分別為：（1）非參數高斯求積法（算法2），簡稱“NP-GQ”；（2）Gauss算法，其均值和標準差用極大似然估計；（3）最大熵方法，其中的核密度估計（帶高斯核）被輸入，在本文中將其簡稱為“NP-ME”。圖1 展示了這三種方法對設定滿足混合分布數據集的概率密度匹配情況。

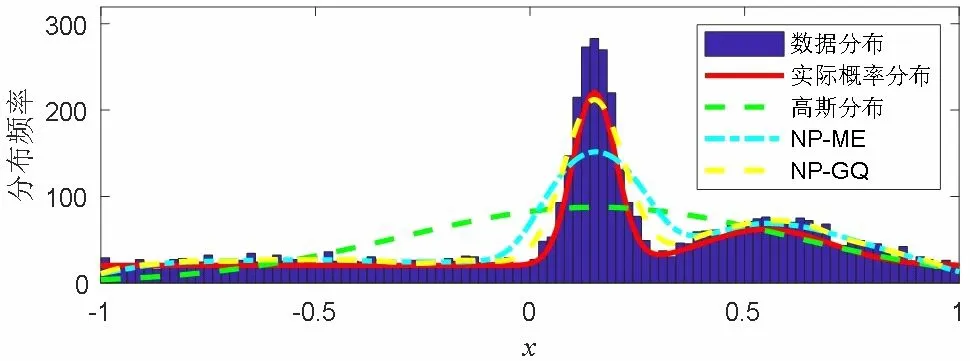
圖1 混合分布數據下概率密度估算對比圖

根據圖1 可以得知，正如所預期，使用Gauss 計算的正態分布無法正確地反映數據規律。NP-ME 方法雖然能夠跟蹤到數據的非參數分布趨勢，但是其精度低于NP-GQ 方法計算出的結果。并且與實際概率分布密度曲線對比可知，NP-GQ 方法的估算結果與其十分接近，此說明了本文所提NP-GQ 方法的有效性。

2.正態分布。在此生成一組滿足均值為1，方差為2 正態分布的數據集，其數據大小為1 000。然后基于此數據集，以觀察非參數高斯求積方法相對于正確指定參數的方法在性能上的區別。將本文提出的非參數高斯求積方法NP-GQ 與Guass 算法和NPME 方法進行了比較，圖2 展示了這一仿真結果。

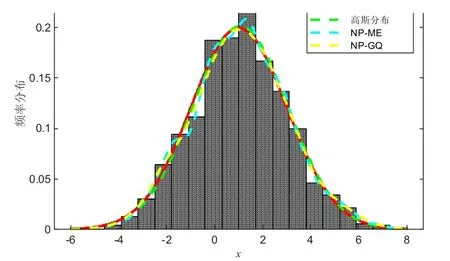
圖2 正態分布數據下概率密度估算對比圖

根據圖中仿真結果表明，工程應用中流行的NPME 方法效果較差。由于Tauchen 方法的不良性能在其他文獻中也有記錄，因此這一結果并不令人驚訝。然而，令人驚訝的是，非參數高斯混合方法（NP-GQ）表現與Guass 算法的結果相似（只是略差于）。并且Guass 算法是求解標準正態分布時的最優的方法。因此，本實驗表明，即使數據的分布情況已被正確指定，使用本文所提的非參數高斯混合也不一定會較大地影響精度。

綜合上述仿真結果可知，若參數分布非混合，本文提出方法不會與標準正態分布存在過大偏差；當參數分布為混合情況或被錯誤指定時，本文提出方法的精確度超過了使用參數分布的精確度。

（二）外商直接投資的核密度估計

在此基于1997—2020 年不同省份外商直接投資額數據，利用本文提出的基于數據的非參數分布自動離散化算法對其進行分析，以2017 年為例分別統計出2017 年利用外商直接投資額的直方圖，非參數分布和參數分布。從圖3 結果可以看出，非參數分布曲線更契合實際的分布直方圖，因此再次佐證，研究外商直接投資的分布特征和演進應該采用非參數分布方法。進一步研究，基于上述算法進行外商直接投資的核密度估計。

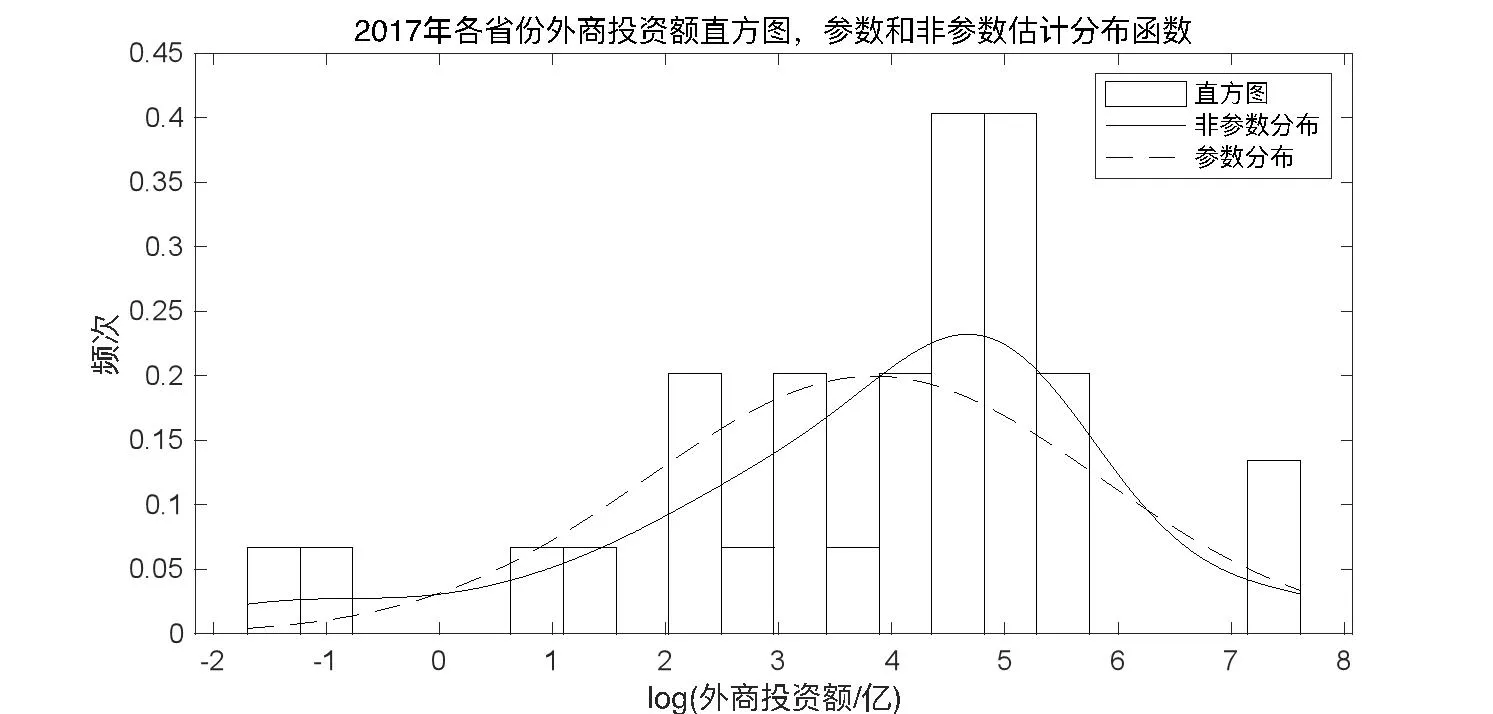
圖3 2017 年不同省份參數與非參數分布的對比圖

以對數外商直接投資額為指標，基于上述所提算法進行核密度估計，準確描繪出外商直接投資的動態分布圖。2000—2020 年周期較長，將全部年份描繪在同一圖中會造成視覺的重疊。因此，將較長的樣本周期按5 年為一個時間節點，觀察2000 年、2005 年、2010 年、2015 年、2020 年這5 個不同年份的趨勢變化。從圖4 可以看出不同時期中國外商直接投資的動態演進圖，通過對圖4 的分析可以把握中國外商直接投資的分布特征。2000—2020 年我國29 個省市外商直接投資額的分布特征表現出兩個特點：（1）密度函數的中心峰度不斷地向右移動，變化區間呈現先變小再變大的趨勢，峰值不斷變大。這可以表明，我國絕大多數的省市外商直接投資的數額在不斷地變大，利用外商直接投資水平不斷提高，省際間的外商直接投資絕對值差距經歷先變小又變大的演變。（2）我國外商直接投資的增長分布也發生比較明顯的變化，波峰由原先的“一主一小”逐漸向“多小一主”的格局演變。2000 年呈現“一主一小”的格局，主峰在左。2005 年仍然呈現“一主一小”格局，但主峰在右。2010 年開始呈現“多小一主”的分布格局，主峰一直在右，多峰形態明顯，表明省際間的外商直接投資額差距不斷增大。

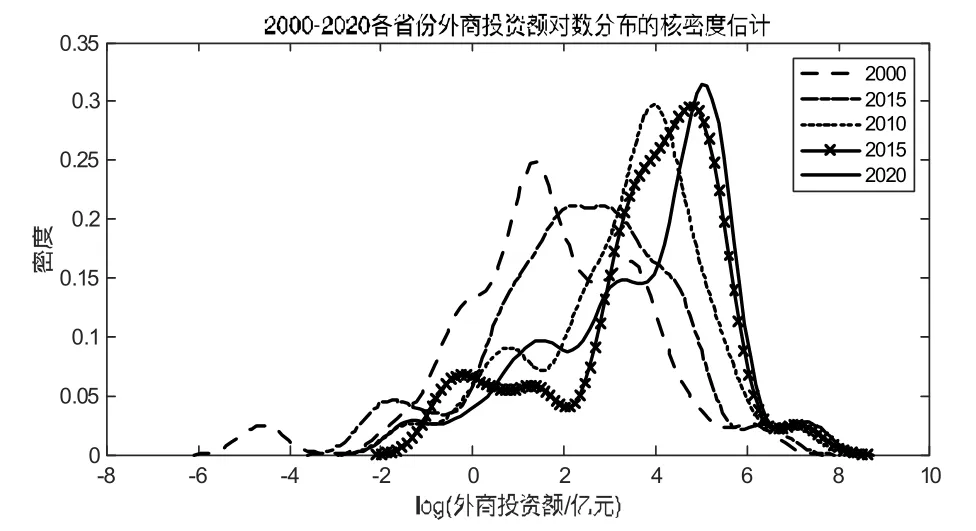
圖4 中國外商直接投資的動態分布圖

五、結論

本文提出一種新的非參數分布自動離散化算法，擬合最優的相關參數，優化非參分布數據下的核密度估計。隨著經濟發展，我國外商直接投資呈現出幾方面的轉變。從政策角度看，政策導向以稅收優惠為主逐漸向以法律制度為主推動外商享受同等國民待遇方面轉變。從結構方面，外商直接投資產業制造業所占比重逐步下降，服務業所占比重日益提升。從區域特點看，東部地區實際利用外資額占據主導地位，但中西部外商直接投資利用額逐步擴大。為此外商直接投資作為國內經濟循環和國際經濟循環的重要銜接點，有望在我國經濟高質量發展中獲得更多商機，繼續保持穩定增長趨勢，在構建新發展格局中發揮獨特功能。