數字金融對綠色創新效率及其收斂性的影響
——以長江經濟帶城市為例

盧淑慧

（貴州大學 經濟學院，貴州 貴陽 550025）

一、引言與文獻綜述

長江經濟帶依托長江黃金水道打造，集中布局了鋼鐵、石化、汽車、機電等一批國家重點工業項目。然而大中型工業企業作為長江經濟帶經濟增長主力軍的同時也破壞了生態環境，粗放式的工業生產模式使得流域結構性污染問題突出[1]。綠色創新是構建沿江綠色發展軸，實現長江經濟帶綠色發展的重要手段之一，但是受長江經濟帶沿江的自然地理條件、經濟地理區位、國家區域開發政策等因素的影響，長江各區域間發展不平衡問題突出[2]。數字金融作為一種金融創新是政府部門和學者關注的熱點，但長江經濟帶區域綠色創新效率是否呈現收斂特征？數字金融對綠色創新效率及其收斂性的影響程度如何？這些問題值得深入探討。

在綠色創新效率的測度方面，諸多學者主要采用DEA[3]、SFA[4]、SBM[5]等模型測算綠色創新效率。在綠色創新效率的收斂性方面，現有文獻從經濟發展水平、政府科技支出、環境規制[5]、教育水平、產業結構、金融支持水平[6]、創新系統主體間的協同關系[7]等方面解釋了區域綠色創新效率收斂速度的差異性。城市創新能力內生于經濟結構，諸如經濟水平、國際貿易水平、金融水平等因素都會不同程度地促進或抑制城市創新能力[8]。金融對綠色創新效率的重要性不言而喻，數字化時代的到來，金融模式發生轉變，數字金融通過降低交易成本、提高資金使用效率、為創新要素在區域間的自由流動提供便利的渠道、豐富企業融資方式[9]、緩解金融錯配、加速人力資本積累[10]等渠道影響綠色創新。

可見，綠色創新效率及其收斂性問題已引起部分學者的關注，也有學者對數字金融與綠色創新進行了多角度探討，但對數字金融對綠色創新效率收斂性的影響卻鮮有提及，這為本研究提供了新的研究視角。基于此，考慮到現有研究的不足，本文以2011—2020 年長江經濟帶108 個城市面板數據為研究單元，使用基于非期望產出的超效率SBM 模型測算區域綠色創新效率，并通過建立空間回歸模型進行數字金融對長江經濟帶城市綠色創新效率及其收斂性的影響研究。

二、理論分析與假說

相較于傳統的金融形式，數字金融從兩個方面影響綠色創新效率。第一，數字金融借助數字化技術形成更為完善的風控體系，保障創新資本安全[10]，推動企業綠色創新項目的實施效率。第二，數字金融憑借數字化技術突破傳統金融的時空限制，有效發揮信息網絡功能，打破信息不對稱壁壘、提高投資和交易的便利性[11]、降低綠色創新主體資金搜尋成本等渠道激勵企業高效開展綠色創新，促進綠色創新效率提升。基于此，提出假說1：

H1：數字金融有利于提高綠色創新效率。

一方面，數字化的金融交易、金融要素等本身具有天然的流動性，體現出較強的空間溢出效應；另一方面，依托數字化技術，數字金融還可以促進其他創新要素在地區間流動，加強創新要素市場關聯度[12]，進而促進了地區創新主體之間的技術交流與合作，發達地區產生較大的技術溢出，有助于欠發達地區進行模仿內化和創新升級，發達地區與欠發達地區在創新領域的差距逐漸縮小，從而幫助區域綠色創新實現收斂發展[13]。基于此，提出假說2：

H2：數字金融有利于提高綠色創新效率的收斂速度。

三、研究方法與數據說明

（一）基準回歸模型

通過建立空間面板模型來研究數字金融對綠色創新效率的影響效應，模型設定如下：

式中：當δ=γ=λ=0 時，為空間滯后模型；當ρ=δ=γ=0 時，為空間誤差模型；當λ=0 時，為空間杜賓模型。μi和ηt表示空間、時間效應，ρ為空間自回歸系數；λ為空間自相關系數；εi，t表示隨機擾動項。

（二）β 收斂分析

收斂理論源于新古典增長理論，最初用于考察不同國家或區域的人均收入水平增速問題，近年來逐漸被延伸至資源環境、能源、農業等不同領域[14]。收斂性分析是研究不同城市間綠色創新效率差距隨時間變化的趨勢，即收斂或發散的特征。現有關于收斂性研究的文獻主要涉及σ收斂、β收斂和俱樂部收斂，而其中β收斂占主導地位[14]。β收斂可以進一步分為絕對β收斂和條件β收斂，結合本文研究內容，前者嚴格假設不同國家或地區有相同的經濟特征，它強調各地區綠色創新效率向同一穩態水平趨近；而條件β收斂則承認不同國家和地區在經濟條件、資源稟賦等各方面的差異，認為各地區綠色創新效率會隨時間推移收斂于各自穩態水平。具體的模型為：

絕對β收斂：

其中，GIi，t+1、GIi，t代表t+1、t時期城市i的綠色創新效率，）即綠色創新效率同比增長率；β為收斂系數，當β＜0 且顯著時說明綠色創新效率呈β收斂趨勢，反之則趨于發散。

條件β收斂：

其中，Xi，t+1為反映城市特征的控制變量，其余變量與上式相同。

經典β收斂僅考察了綠色創新效率在時間演變上的收斂特征，未考慮到地區間相關性。因此，為避免收斂結論的有偏性[14]，本文引入空間計量方法，建立空間β收斂模型對長江經濟帶綠色創新效率的收斂特征進行檢驗，具體模型設定如下：

空間絕對β收斂：

式中：當δ=λ=0 時，為空間滯后模型；當ρ=δ=0時，為空間誤差模型；當λ=0 時，為空間杜賓模型。

空間條件β收斂：

式中：當δ=λ=0 時，為空間滯后模型；當ρ=δ=0時，為空間誤差模型；當λ=0 時，為空間杜賓模型。

另外，根據收斂系數的估計值還可以計算綠色創新效率收斂速度υ和收斂半衰期τ，即落后城市追趕上發達城市所需要的時間。計算公式如下：

（三）空間權重矩陣的構建

本文使用地理距離權重矩陣，即隨著地理距離的拉大，綠色創新效率水平的聯系越小，反之則越大。

（四）變量與數據介紹

1.被解釋變量。被解釋變量——綠色創新效率（GI）：綠色創新效率的估算需要明確投入變量、期望產出變量與非期望產出變量。本文參考許玉潔和劉曙光（2022）[3]的做法，選科學技術支出、科技服務人員分別作為綠色創新勞動和資本投入；資源投入方面，使用供氣總量（煤氣、天然氣）、液化石油氣供氣總量和全社會用電量分別折標準煤后的總和衡量能源投入；對于綠色創新產出，使用CNRDS 統計的綠色發明和綠色實用新型數量；考慮到長江經濟帶資源粗放利用帶來流域結構性污染問題，選取工業廢水、工業二氧化硫、工業煙（粉）塵排放量作為非期望產出。

2.核心解釋變量。數字金融發展指數（DF）：本文使用北京大學數字普惠金融指數作為各地區數字金融發展的代理變量。

3.控制變量。本文參考成瓊文等（2020）[15]、聶秀華等（2021）[9]的研究，選取以下與綠色創新效率有關的變量作為控制變量。其中，平均企業規模（MCS）使用規模上工業企業生產總值和規模上工業企業數的比值衡量；產業結構（IS）使用各地第二產業增加值與地區生產總值的比值來衡量；外商直接投資（FDI）使用各地外商直接投資額與地區生產總值的比值衡量。

綠色發明和綠色實用新型數量來自CNRDS、外商直接投資來源于CSMAR，其余數據來源于《中國城市統計年鑒》《中國環境統計年鑒》《中國能源統計年鑒》以及各省市統計年鑒。部分缺失數據由插值法補齊。

四、實證分析

在進行模型參數估計之前，需要對綠色創新效率的空間相關性予以檢驗，以及對空間計量模型進行比選。首先，在整個研究期間，綠色創新效率Moran's I 指數顯示綠色創新效率在空間分布上呈顯著的正相關性，臨近城市間的綠色創新效率存在空間依賴性（見表1）。其次，本文結合LM 檢驗、穩健LM 檢驗和AIC 準則篩選最佳模型，最后基準回歸模型選用空間杜賓模型，β收斂分析選用空間誤差模型。

表1 長江經濟帶綠色創新效率的全局莫蘭指數

（一）數字金融對綠色創新效率的影響分析

表2 展示了數字金融對綠色創新效率影響的空間杜賓回歸結果。結果表明不管從長江經濟帶整體，還是從上游中游下游區域來看，核心解釋變量數字金融的系數均在5%水平上顯著為正，即數字金融對綠色創新效率有正向促進作用，因此H1 得以驗證。

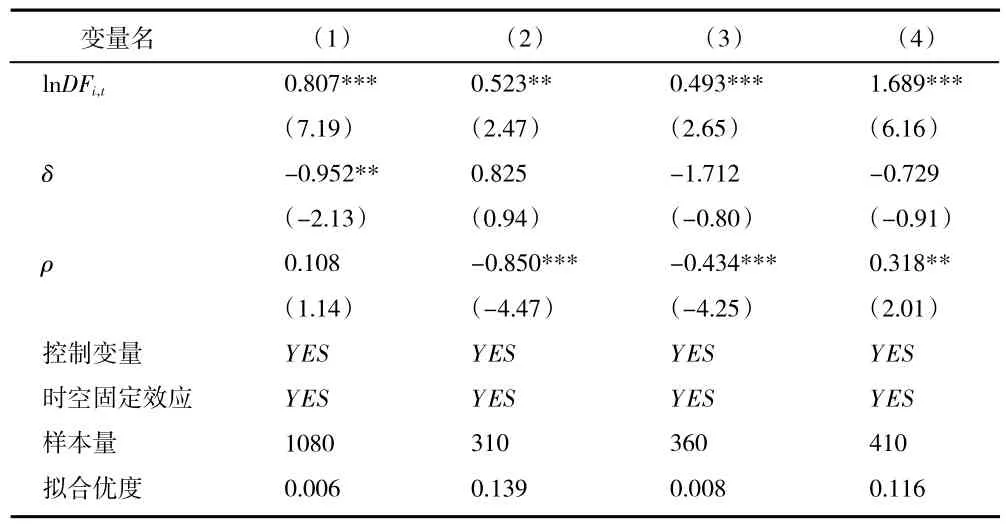
表2 基準回歸結果

（二）絕對β 收斂分析

表3 中模型（5）～模型（8）分別報告了長江經濟帶整體、上游、中游、下游地區綠色創新效率的絕對β收斂檢驗結果。首先，長江經濟帶整體及各區域收斂系數β均顯著為負，說明長江經濟帶整體及內部各區域綠色創新效率水平存在絕對β收斂趨勢。其次，在長江經濟帶整體層面，空間系數λ在1%水平顯著為正，表明長江經濟帶內部城市之間綠色創新效率的空間正向關聯較強，即鄰近城市的綠色創新效率越高，本城市的綠色創新效率越高，反之亦然，因此，長江經濟帶整體各城市間的互動合作有利于提升長江經濟帶整體綠色創新效率。最后，對比長江經濟帶上游、中游、下游地區綠色創新效率的收斂速度和半衰期，可以發現下游地區的收斂速度最慢，中游地區次之、上游地區的收斂速度較快。

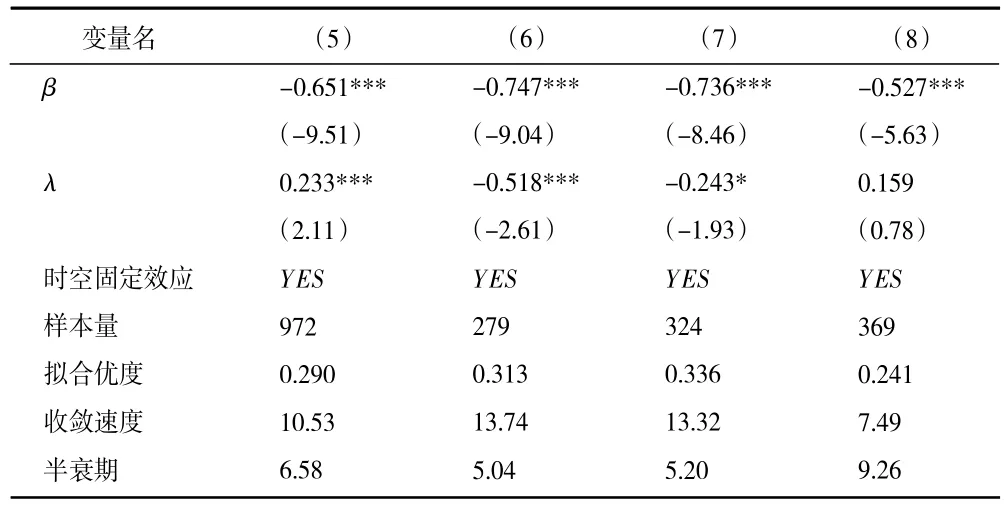
表3 絕對β 收斂回歸結果

（三）條件β 收斂分析

借鑒層次回歸和逐步回歸的思想[16]，將表4、表5 的模型分為三類，第一類模型（9）～模型（12）只加入核心的數字金融指標，驗證長江經濟帶整體、上游、中游、下游綠色創新效率條件收斂β是否存在；第二類模型（13）～模型（16）加入核心變量和其他控制變量；第三類模型（17）～模型（20）只加入其他控制變量。本文主要通過對比第二類和第三類模型的收斂速度，識別數字金融對綠色創新效率β收斂的影響；通過第二類模型的解釋變量的系數來說明數字金融發展及其他控制變量對綠色創新效率收斂性的影響。

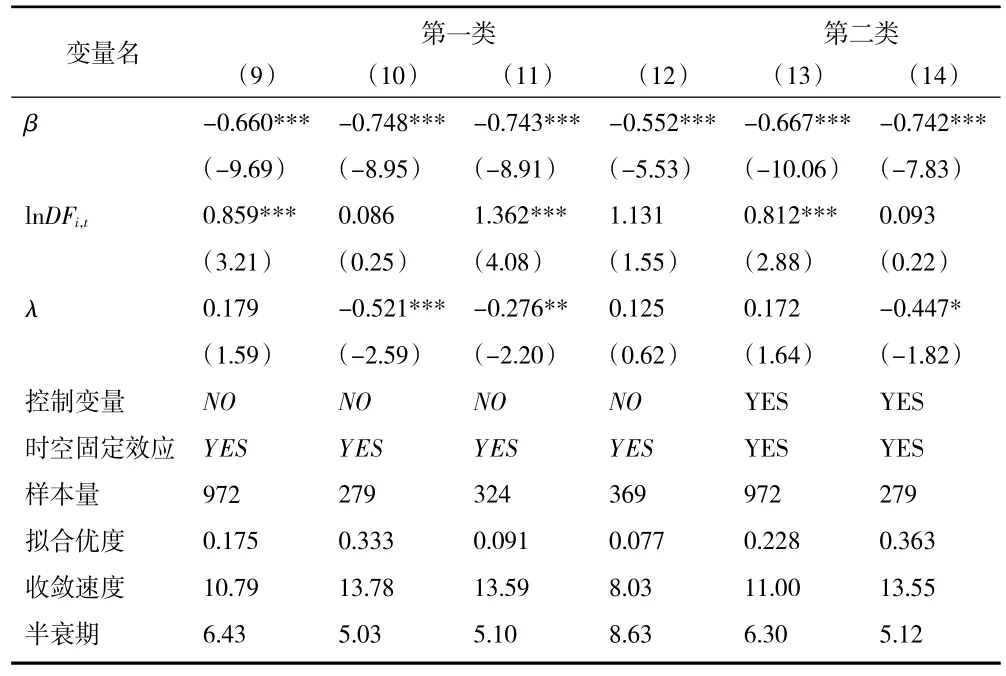
表4 條件β 收斂回歸結果

表5 條件β 收斂回歸結果

第一，根據表4、表5 的三類模型結果可以看出，2011—2020 年長江經濟帶整體及內部各區域綠色創新效率均存在顯著的條件β收斂趨勢，即各區域綠色創新效率會隨時間推移趨于各自的穩態水平。另外，條件收斂的收斂速度均大于絕對收斂的速度。這是由于條件收斂考慮了地區間社會經濟條件、技術水平等的異質性，加快了綠色創新效率的收斂速度，并縮短了半衰期，從而使得收斂性檢驗更加準確可靠。

第二，根據第二類、第三類模型結果之間的對比可知，第二類模型相比于第三類模型，長江經濟帶整體、上游、中游、下游綠色創新效率的收斂速度更快，半衰期更短，但速度提高值有限，半衰期縮短時間不超過1 年，其中，下游地區收斂速度提升效應最明顯，說明數字金融發展水平正向促進綠色創新效率的β收斂性，即各城市可以通過發展數字金融加速綠色創新效率趨于各自的穩態水平。因此H2得以驗證。

第三，在區域層面，三類模型均顯示長江經濟帶上游、中游地區收斂速度較快，半衰期相對較短；下游地區收斂速度較慢，半衰期相對較長的現象。這說明在長江經濟帶上游、中游、下游三大地區的數字金融對綠色創新效率的促進作用存在一定的差異性。出現的原因可能在于長江經濟帶整體經濟基礎良好，但區域內差異較大，其中長江經濟帶下游地區憑借優越的地理位置，經濟總量和技術水平處于長江經濟帶“龍頭”地位，基礎設施建設和資源稟賦都優于上游、中游地區，技術與資本的投入對綠色創新效率提升的邊際效應在遞減，使得綠色創新效率的收斂速度相對略慢，相比之下，長江經濟帶上游、中游地區的綠色創新效率水平提升空間大，“后發趕超”優勢明顯。

（四）穩健性檢驗

為了保證研究結論的可靠性，本文通過構造經濟地理嵌套矩陣替代地理距離矩陣進行穩健型檢驗。經濟地理嵌套矩陣同時蘊含了經濟和地理因素，將地理距離權重矩陣和經濟距離權重矩陣有機結合起來。

結果顯示，采用新的空間權重以后，長江經濟帶綠色創新效率收斂系數和數字金融驅動系數的方向和顯著性并沒有發生明顯變化。這表明模型空間權重的變化并沒有改變前文的基本結論。結果具有穩定性。限于篇幅，僅展現長江經濟帶整體層面回歸結果，其余回歸結果備索（見表6）。

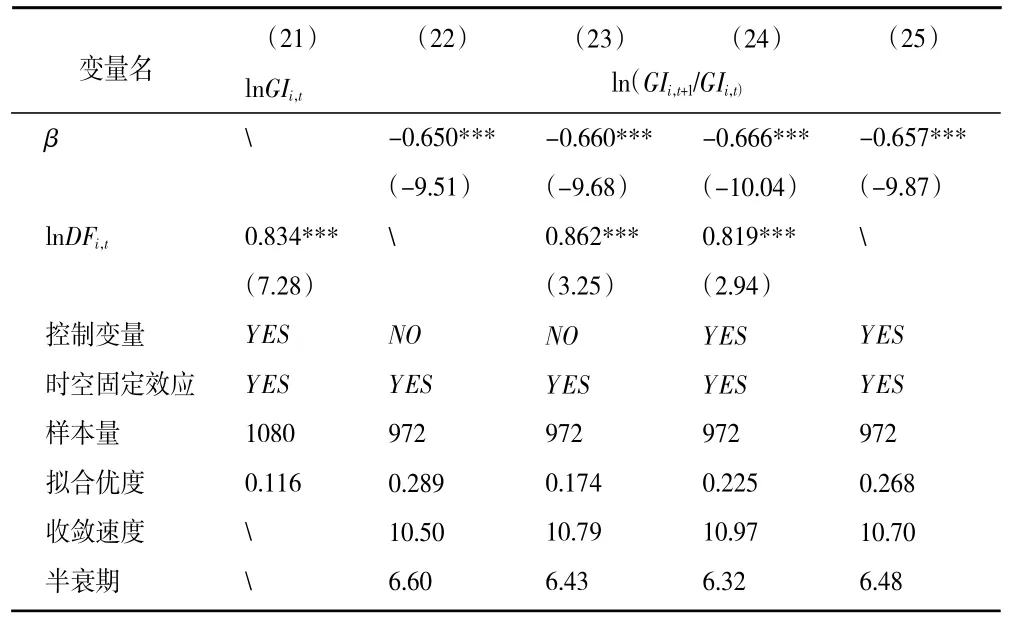
表6 穩健性回歸結果

五、結論與建議

本文運用基于非期望產出的超效率SBM 模型對長江經濟帶各城市綠色創新效率進行測度，通過構建空間面板模型，實證考察了數字金融對長江經濟帶區域綠色創新效率及其收斂性的影響。研究結果表明：

第一，長江經濟帶數字金融與綠色創新效率呈正相關關系。數字金融的發展有利于綠色創新效率的提升。第二，使用空間絕對β收斂模型和空間條件β收斂模型探討長江經濟帶地區的綠色創新效率收斂特征，發現長江經濟帶整體及各區域綠色創新效率均存在顯著的絕對β收斂和條件β收斂特征，其中，上游地區和中游地區收斂速度較快、下游地區的收斂速度較慢。第三，進一步借鑒層次回歸和逐步回歸的思想，比較加入和未加入數字金融的空間條件β收斂模型，對比兩類模型的收斂速度和半衰期的變化發現數字金融發展加快了長江經濟帶整體及各區域綠色創新效率的收斂速度，有利于綠色創新效率的收斂。

基于上述結論，本文提出以下建議。第一，積極探索建立長江經濟帶各區域之間的協調發展機制，搭建區域合作平臺，增強區域間的交流與合作，爭取早日實現長江經濟帶綠色協同發展。第二，以數字金融為契機，努力推動數字金融對綠色創新效率的促進作用和收斂作用。針對數字金融高創新性、強滲透性、廣覆蓋性的特點，加強建設經濟金融市場生態環境，全面推進長江經濟帶數字金融的深層次建設，讓數字金融成為實現長江經濟帶綠色協同發展的重要引擎。