考慮季節性氣候因子的配電網可中斷負荷預測方法探析

【關鍵詞】配電網；可中斷負荷；季節性氣候因子；支持向量機；最優函數

引言

可中斷負荷作為一種靈活的電力需求側管理措施，可以在系統負荷高峰時段通過中斷部分非關鍵負荷供電[1-2]，緩解電網供電壓力，保障重要負荷的供電需求。因此，對配電網可中斷負荷進行優化研究，能夠為電力系統優化調度和能源管理提供支持。

劉佳等（2023）提出考慮停電損失及可中斷負荷的有源配網魯棒孤島劃分策略[3]，但是，該方法未考慮季節性氣候因子對分布式能源出力的影響。趙智忠等（2022）提出考慮可中斷負荷接入的主動配電網魯棒優化模型[4]，但是，該方法模型求解過程中容易產生數據冗余。Sajjad等（2023）基于負荷控制需求響應的主動配電系統規劃，構建主動配電系統規劃模型，并采用多目標優化算法進行求解[5]。

季節性氣候因子是指隨著季節變化而變化的氣候要素，如溫度、濕度、日照時間等。不同季節的氣候條件會直接影響用戶用電行為，同時還會影響供電系統的穩定性，導致供電中斷風險增加。因此，通過考慮季節性氣候因子進行可中斷負荷預測，能夠有效保障供電系統穩定性。基于此，本文引入季節性氣候因子，提出一種新的配電網可中斷負荷預測方法。

一、配電網可中斷負荷預測方法

（一）季節性氣候因子數據收集與預處理

假設t時刻的歷史配電網可中斷負荷序列為Y（t），計算第p種日類型t時刻的平均負荷如式（1）所示：

式（1）中，m為第p種日類型的總數量，Yp（j，t）為第j日中t時刻的可中斷負荷值。

將可中斷負荷數據維度固定在［0，1］之間，設定歸一化過程中原始可中斷負荷數據為Ays，歸一化處理如式（2）所示[6]：

式（2）中，Amin和Amax分別為原始可中斷負荷數據最小值和最大值。

依據可中斷負荷數據的歸一化結果，建立可中斷負荷特征向量集Bi，獲取第i個可中斷負荷數據的第j個季節性氣候因子對應的灰色關聯值，如式（3）所示：

式（3）中，Y為季節性氣候因子的時間序列平均值，rj為第j個季節性氣候因子的權重，Hpq負荷影響系數，n為季節性氣候因子的總數。

使用降序排列法對不同季節性氣候因子Bij實施排列處理，選擇1ijB≥的數據作為季節性氣候因子數據集。

使用最小二乘算法推斷季節性氣候因子數據集中殘缺數據，如式（4）所示：

式（4）中，Di為平均日照率，w為氣溫季節性變動系數，b為逼近不確定缺失值的偏差值。

利用二次指數平滑法修正季節性氣候因子數據，消除數據中的異常值，如式（5）所示：

式（5）中，α為平均氣溫，St1為原始季節性氣候因子數據序列中的t1項，St2為原始季節性氣候因子數據序列中的t2項。

（二）季節性氣候因子特征提取

根據修正后的季節性氣候因子數據，研究選擇與配電網可中斷負荷預測相關性較高的氣候因子作為特征，分析每個季節性氣候因子對應的時間序列F，如式（6）所示：

二、測試與分析

（一）測試環境

甘肅武威位于我國西北地區，不同季節的用電行為存在明顯差異：夏季空調、制冷設備使用頻次較多，容易增加電力負荷；冬季取暖設備再次增加地區用電量。因此，研究利用PSCAD仿真軟件構建包含架空線路、纜線混合線路和電纜線路的110 kV配電網仿真模型。

（二）測試數據

訓練樣本數據為國網武威供電公司電力調度中心2022年1月至12月的實際電力數據記錄。選擇50組可中斷負荷數據作為測試數據，每組數據集包括2000個電力數據，共計100，000個，采樣頻率為1 M/s，共獲得測試數據約35 GB。

（三）測試結果與分析

將劉佳等（2023）方法（考慮停電損失及可中斷負荷的有源配網魯棒孤島劃分策略）、趙智忠等（2022）方法（考慮可中斷負荷接入的主動配電網魯棒優化模型）和Sajjad等（2023）方法（基于負荷控制需求響應的主動配電系統規劃）作為對照方法，與本文方法在相同測試環境和測試數據條件下進行對比測試。

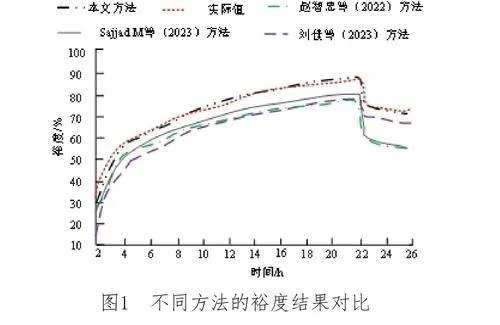
1.可中斷負荷裕度測試

可中斷負荷裕度是指在一定時間段內，配電網系統能夠承受的最大負荷波動范圍；即電力系統在承擔某一時段內的最大負荷時，與該最大負荷之間的剩余能力比例。在負荷高峰或突發情況下，可中斷負荷裕度不足，可能會導致配電網無法及時響應。較高的可中斷負荷裕度表明配電網具有更大的備用容量和靈活性，可以更好地應對可中斷負荷波動。可中斷負荷預測的準確性直接影響可中斷負荷裕度計算，若可中斷負荷裕度計算結果與實際結果吻合，表明算法對可中斷負荷預測的精度較高。不同方法的可中斷負荷裕度結果如圖1所示。

根據測試結果，本文方法的可中斷負荷裕度與實際結果基本吻合，而對照方法的可中斷負荷裕度均低于實際值。這是因為本文方法使用最小二乘算法推斷季節性氣候因子的數據集中殘缺數據；通過映射函數將已知數據與缺失季節性氣候因子數據建立聯系，補充缺失值，提高數據集的準確性和可靠性；利用二次指數平滑法對季節性氣候因子數據進行平滑處理，消除數據中的異常值，使數據更加平滑和穩定，進而提高可中斷負荷預測準確性。

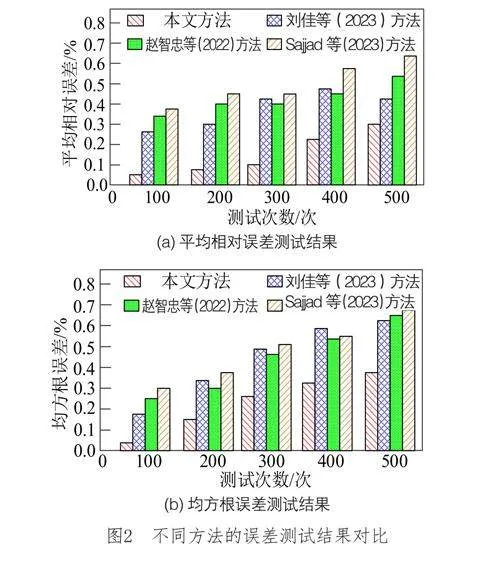
2.可中斷負荷誤差測試

平均相對誤差是各個預測值與實際值之差的絕對值的平均數，反映了模型預測值與實際值之間的平均偏差程度。均方根誤差是各個預測值與實際值之差的平方值的平均數的平方根，能衡量模型預測值與實際值之間的離散程度。研究選擇平均相對誤差和均方根誤差作為測試指標，衡量不同方法的可中斷負荷預測性能，具體測試結果如圖2所示。

通過分析圖2可以看出，在相同測試次數下，不同方法的平均相對誤差和均方根誤差均存在明顯差異，所提方法的誤差結果明顯低于對照方法。這是因為本文方法通過整合不同季節性氣候因子相似度，更全面地捕捉與可中斷負荷相關的季節性變化規律；同時，對季節性氣候因子相似度進行降維，去除冗余信息后提取季節性氣候因子特征，使模型更專注于最重要特征，提高模型泛化能力。由此證明，采用本文方法可以獲取高精度的可中斷負荷預測結果。

結語

本文提出的考慮季節性氣候因子的配電網可中斷負荷預測方法，通過一系列數據處理和優化手段，有效提升了可中斷負荷預測的準確性。該方法不僅為配電網的安全穩定運行提供了保障，也為電力市場的供需平衡和資源配置優化提供了有力支持。