利用長短期記憶神經(jīng)網(wǎng)絡(luò)的改進POD-Galerkin降階模型及其在流場預(yù)測中的應(yīng)用

張譯文,王志恒,邱睿賢,席光

(西安交通大學(xué)能源與動力工程學(xué)院,710049,西安)

由Navier-Stokes (N-S)方程所描述的流體流動具有非線性和多尺度特征,其固有的復(fù)雜性使得預(yù)測流體流動十分困難。計算流體動力學(xué) (computational fluid dynamics,CFD) 方法可以通過基于偏微分方程的全階模型 (full order model,FOM) 提供對流體流動的準確預(yù)測,但是計算量可能較大,無法做到實時預(yù)測。因此,構(gòu)建低成本流場降階模型 (reduced order model,ROM) 有很高的應(yīng)用潛力[1]。流場降階模型是指從CFD 或?qū)嶒灥玫降臄?shù)據(jù)集而構(gòu)建的低維數(shù)學(xué)模型,可以預(yù)測流場參數(shù)。與基于CFD 的分析相比,ROM 可以在很短的時間內(nèi)準確預(yù)測線性和非線性空氣動力學(xué)過程,速度能夠加快1～2個數(shù)量級[2],因而在流場快速預(yù)測與實時控制中具有重要的應(yīng)用價值。

根據(jù)是否將流動控制方程加入至模型,降階模型可分為侵入式降階模型和非侵入式降階模型兩類。侵入式降階模型將本征正交分解(proper orthogonal decomposition,POD)得到的正交基通過伽遼金(Galerkin)投影的方式投影至流動控制方程上,以此得到由模態(tài)時間系數(shù)構(gòu)建的低維模型,因此也稱為Galerkin投影式降階模型[3]。由于考慮了控制方程,侵入式降階模型能夠?qū)-S方程中各物理項進行解釋,進而定量分析出各項的作用大小。近年來,對POD-Galerkin降階模型有較多應(yīng)用研究。康偉等[4]提出了一種利用POD的非線性Galerkin方法,用于復(fù)雜流體動力系統(tǒng)的低維建模,并以雷諾數(shù)為200、攻角為20°時的NACA0012翼型繞流流動問題為例進行了低維建模分析。Aubry等[5]對湍流邊界層過渡流動進行了建模,結(jié)果表明降階模型捕捉到了實驗觀察到的流向渦對運動形態(tài)。Deane等[6]重構(gòu)了周期性凹槽通道中的流動和孤立圓柱體的尾流,研究了模型的短期和長期精度,并對構(gòu)建降階模型所用工況之外的工況點進行了測試,結(jié)果表明周期性凹槽中流動降階模型在Re附近能夠進行合理的外推。Noack等[7-8]對 Galerkin 模型進行了改進,引入了一種移位模態(tài),使得POD-Galerkin降階模型能夠重構(gòu)瞬態(tài)動力學(xué)過程,并以3階動力學(xué)系統(tǒng)重構(gòu)了Re=100的孤立圓柱繞流。張鴻志等[9]以AGARD 445.6機翼為對象,研究了ROM建立過程中不同參數(shù)對于模型精度的影響,并將ROM應(yīng)用于顫振邊界的預(yù)測。李靜等[10]以低雷諾數(shù)下圓柱繞流為對象,構(gòu)建失穩(wěn)初期的流動ROM,該模型可以復(fù)現(xiàn)流場發(fā)散初期的發(fā)生趨勢。馮俞楷[11]和梁鈺[12]對非穩(wěn)態(tài)導(dǎo)熱問題構(gòu)建ROM,給出了渦輪葉片瞬態(tài)非線性熱傳導(dǎo)問題的求解結(jié)果,該模型大大提高了計算速度,實現(xiàn)了快速預(yù)測。非侵入式降階模型又稱為數(shù)據(jù)驅(qū)動式降階模型,它不需要給出明確的控制方程,直接從流場的高維流動數(shù)據(jù)中構(gòu)建。非侵入式降階模型可以通過輸入、輸出量直接建立線性或非線性黑盒模型[13],也可以通過對流場測量數(shù)據(jù)建立簡化流動模型,如代理模型[14]、人工神經(jīng)網(wǎng)絡(luò)[15]、非線性系統(tǒng)辨識[16]等。非侵入式降階模型憑借其模塊化的優(yōu)勢[17],在流場降階模型研究中越來越受到研究者們的關(guān)注。Duraisamy等[18]、Saeed等[19]和Reddy等[20]使用機器學(xué)習(xí)方法提高CFD模擬的準確性,以神經(jīng)網(wǎng)絡(luò)來預(yù)測流場不同流動條件和幾何形狀下的速度和壓力場,相較于CFD能夠更快地估計流場變化情況。

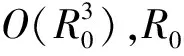
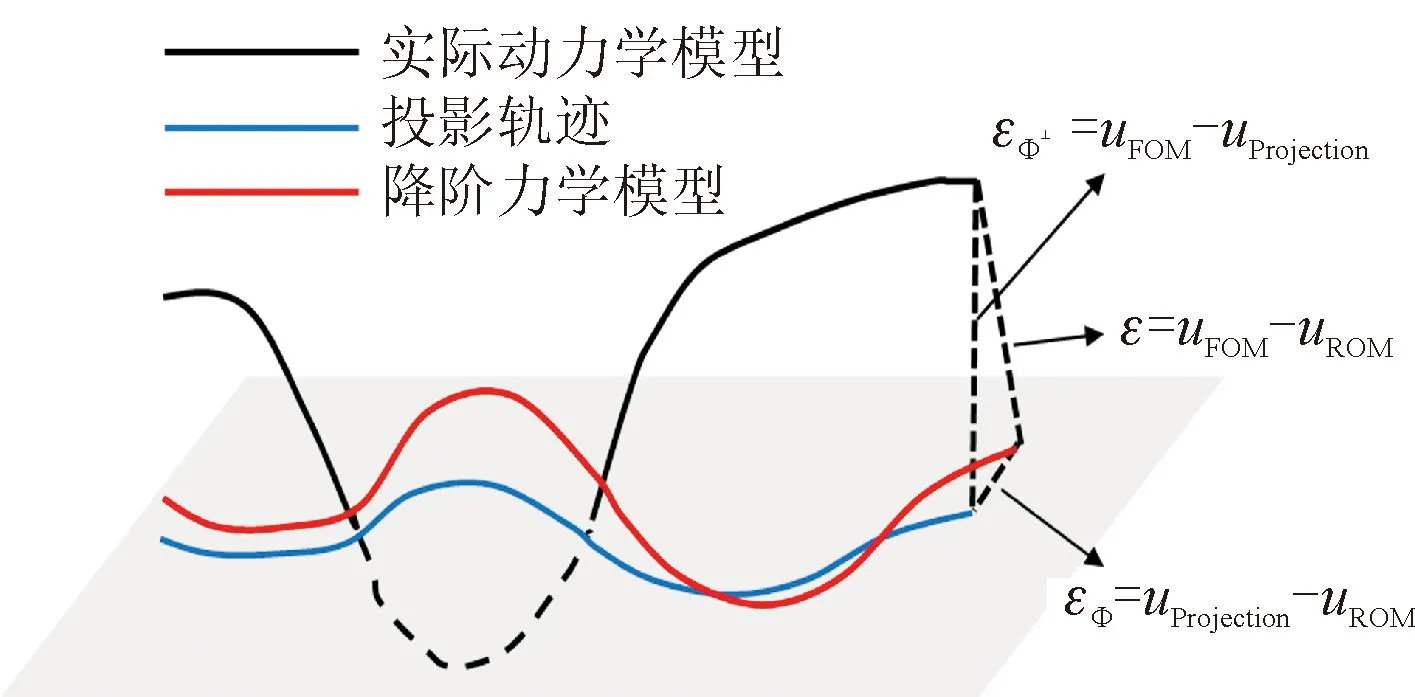
圖1 降階模型中誤差來源Fig.1 Error sources in reduced order models

針對上述POD-Galerkin降階模型存在的誤差,通過對模型進行修正,添加額外的作用項使得降階模型預(yù)測軌跡與實際軌跡相符,是切實可行的方法[24-25]。鑒于機器學(xué)習(xí)方法在提取特征方面的優(yōu)勢,其與流場降階方法結(jié)合有更大的潛力。基于此,本文提出一種引入長短期記憶神經(jīng)網(wǎng)絡(luò)(long short-term memory,LSTM)[26]的改進POD-Galerkin降階模型。該模型通過Galerkin投影來提高降階模型的可解釋性,并通過兩個不同的長短期記憶神經(jīng)網(wǎng)絡(luò)分別進行大尺度模態(tài)的誤差修正和小尺度模態(tài)的階數(shù)擴展。將改進的POD-Galerkin降階模型應(yīng)用于典型的二維圓柱繞流問題的流動預(yù)測,通過與標準POD-Galerkin降階模型的對比,以驗證改進降階模型的有效性和可靠性。

1 引入神經(jīng)網(wǎng)絡(luò)的改進POD-Galerkin降階模型

1.1 POD-Galerkin降階模型

POD-Galerkin降階模型可將高階的偏微分方程組轉(zhuǎn)化為低階的常微分方程組,其在流場降階中應(yīng)用的基本思路是:將數(shù)值模擬或?qū)嶒灥玫降牧鲌鰠?shù)作為樣本數(shù)據(jù),采用 POD方法[27]得到描述流場的一組最佳正交模態(tài),并對低能量模態(tài)進行截斷,然后將 N-S 方程投影到主要模態(tài)上,得到關(guān)于模態(tài)系數(shù)的一組常微分方程組,從而將高階問題轉(zhuǎn)化為低階非線性動力學(xué)問題。具體建模過程如下。

對于流場數(shù)據(jù)U(x,t),將每個時刻的流場構(gòu)成一列數(shù)據(jù),選取樣本庫中N個時刻的數(shù)據(jù)作為樣本,構(gòu)建流場快照矩陣

(1)

(2)

式中:ai為第i階POD模態(tài)時間系數(shù)。

對于不可壓N-S方程,在截取的前階特征模態(tài)上作Galerkin投影。投影通過N-S方程與POD模態(tài)內(nèi)積得到,表示為

(3)

式中:u為速度矢量;p為壓力;ν為運動黏度;(,)為內(nèi)積運算符。由此可得m個常微分方程構(gòu)成的常微分方程組

(4)

式中:Ak、Bk、Ck均為常數(shù)項,可以由速度場、速度場梯度項、壓力場、壓力場梯度項的組合求得。由格林定理和無散度的性質(zhì)可知,在出口邊界p=0的情況下,壓力項可以消去。通過求解上述常微分方程組,即可獲得各階模態(tài)時間系數(shù)的變化趨勢,與POD空間模態(tài)結(jié)合,可以重構(gòu)原始流場。

1.2 神經(jīng)網(wǎng)絡(luò)的引入

針對標準POD-Galerkin降階模型存在的兩個主要誤差來源,可以分別添加神經(jīng)網(wǎng)絡(luò)項來提高降階模型的精度。對于第一個誤差來源,對流場進行POD后,對高階模態(tài)進行截斷忽略了高階模態(tài)在流場中的耗散作用,保留的低階模態(tài)失去了與高階模態(tài)的耦合項,使得耗散誤差不斷累積,會影響構(gòu)建的動力系統(tǒng)的長期穩(wěn)定性。因此,可以通過POD分解得到的時間系數(shù)與構(gòu)建的降階動力學(xué)系統(tǒng)誤差引入長短期記憶神經(jīng)網(wǎng)絡(luò)[28],建立輸入-輸出關(guān)系,以此修正降階模型與實際預(yù)測值之間的偏差。

定義實際的動力學(xué)系統(tǒng)模型

(5)

從實際動力學(xué)系統(tǒng)中可以求得變量ak隨時間變化的離散值ak(t1),ak(t2),…,ak(tn)等。

假設(shè)降階動力學(xué)系統(tǒng)模型為

(6)

對此動力學(xué)模型,通過求解線性微分方程組可以得到下一時刻的時間系數(shù)

(7)

(8) 式中:ck為降階模型預(yù)測值和真實投影之間的誤差。為修正此誤差,可以利用LSTM架構(gòu)來學(xué)習(xí)矯正項,在每個時間步內(nèi),LSTM神經(jīng)網(wǎng)絡(luò)將模態(tài)系數(shù)從降階模型的預(yù)測值引導(dǎo)至真實值上。

(9)

(10)

綜上所述可知,整個神經(jīng)網(wǎng)絡(luò)修正過程包括兩個階段,首先通過第一個LSTM神經(jīng)網(wǎng)絡(luò)映射來減小第一部分誤差,然后通過第二個LSTM神經(jīng)網(wǎng)絡(luò)擴展模態(tài)階數(shù)來減小第二部分誤差。引入神經(jīng)網(wǎng)絡(luò)的改進POD-Galerkin降階模型的計算流程如圖2所示。

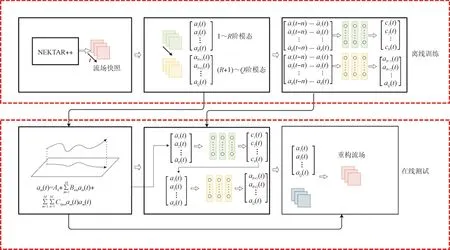
圖2 改進POD-Galerkin降階模型流程Fig.2 Flowchart of improved POD-Galerkin reduced order model

離線訓(xùn)練期間,模型在不同時間節(jié)點獲得真實的流場信息,進而可以計算得到真實的POD模態(tài)時間系數(shù)。首先通過標準POD-Galerkin降階模型逐步計算每個時間步長的模態(tài)系數(shù),然后計算f和g兩個LSTM項。

在線測試期間,首先從時間零點開始,將當前時刻的流場快照投影到前R階模態(tài)上獲得初始時刻的模態(tài)時間系數(shù),然后通過標準POD-Galerkin降階模型進行第一個時間步長的計算。得到第一個時間步長上的模態(tài)時間系數(shù)后,通過LSTM修正項f計算得到預(yù)期的誤差ck,再進行第一次的修正,隨后通過LSTM擴展項g計算得到擴展模態(tài)時間系數(shù),利用兩個部分得到的模態(tài)時間系數(shù)以及保留的前Q階靜態(tài)空間流場模態(tài),即可得到高精度的預(yù)測流場。

2 改進POD-Galerkin降階模型的應(yīng)用

將提出的引入神經(jīng)網(wǎng)絡(luò)修正的改進POD-Galerkin降階模型應(yīng)用于典型二維圓柱繞流問題的流場預(yù)測。研究對象為Re=100條件下圓柱繞流,其來流馬赫數(shù)較小(Ma<0.1),可以視作不可壓縮流動,且傳熱較小可以忽略,因此在進行數(shù)值模擬時僅考慮質(zhì)量守恒方程和動量方程

(11)

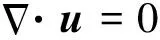
(12)

本文利用 NEKTAR++軟件對圓柱繞流進行直接數(shù)值模擬,利用 hp 型譜元法直接對流場控制方程組進行求解,求解方法采用經(jīng)典伽遼金公式與譜元離散相結(jié)合的高階有限元方法,對每個網(wǎng)格單元內(nèi)部的節(jié)點值通過 Gauss-Lobatto-Legendre多項式的拉格朗日展開來近似。

圓柱繞流的計算區(qū)域如圖3所示。將圓柱直徑D作為無量綱處理的特征長度,取D=1,圓柱圓心位于原點,入口和出口邊界位于x=-10D和x=20D處,垂直于流向方向長度為-10D～10D。進口速度采用無窮遠來流速度進行無量綱處理。

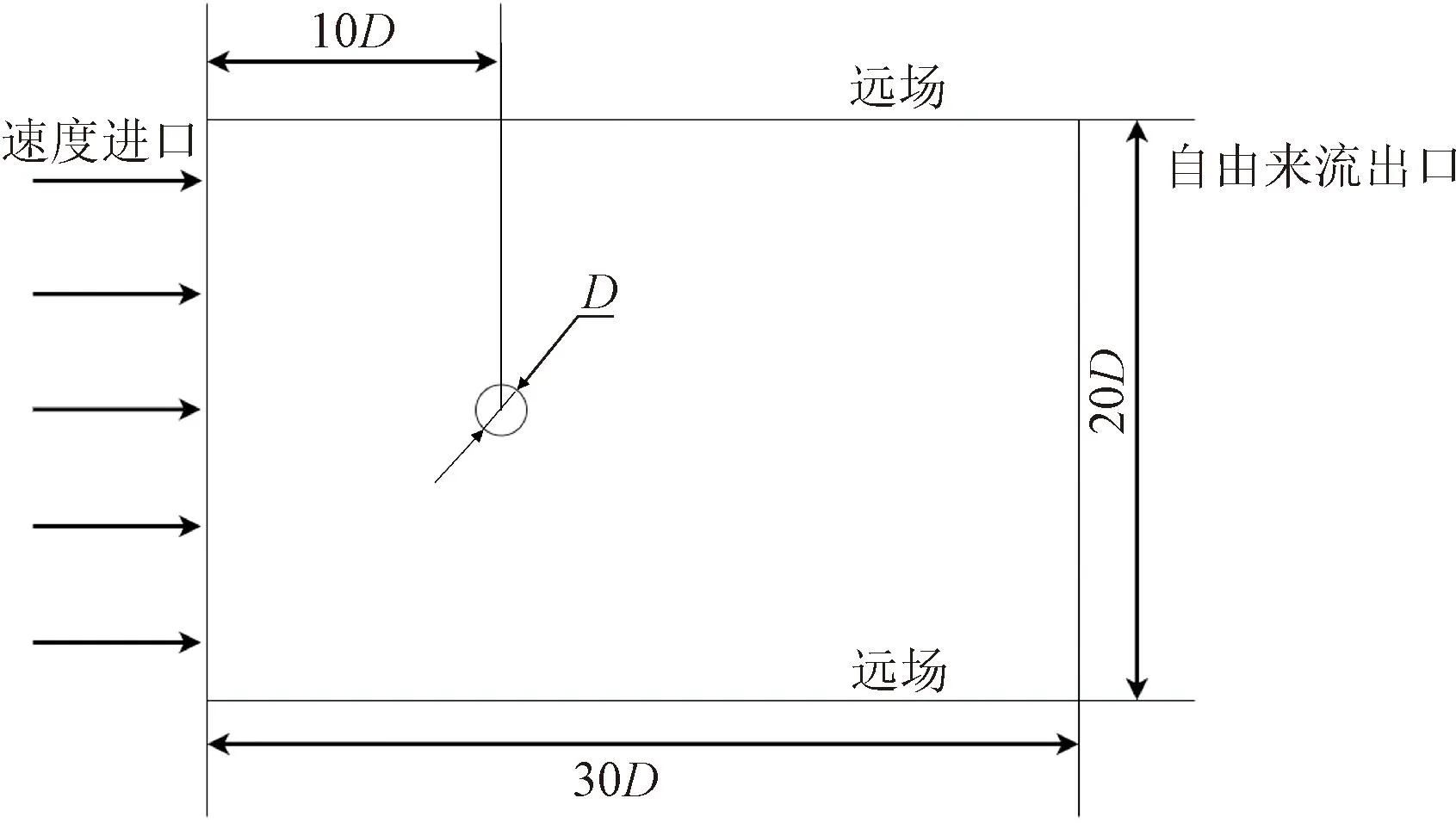
圖3 圓柱繞流計算域Fig.3 Computational domain of flow around a cylinder

圓柱繞流的流場網(wǎng)格如圖4所示,進口采用均勻速度進口,出口采用自由流出口,用以消除尾跡的影響,圓柱壁面采用無滑移邊界。上下邊界采用對稱邊界,以避免壁面對圓柱的影響。在圓柱附近進行網(wǎng)格加密處理,最終的網(wǎng)格節(jié)點總數(shù)為31 360。

圖4 圓柱繞流的流場網(wǎng)格劃分及局部加密圖 Fig.4 Computational mesh and grid refinement near the cylinder surface

根據(jù)邊界條件進行非定常計算,待尾跡穩(wěn)定振蕩后采樣20個周期的流場數(shù)據(jù)。定義升力系數(shù)Cl、阻力系數(shù)Cd及斯特勞哈爾數(shù)St為

(13)

(14)

(15)

式中:Fl為圓柱所受到的升力;Fd為圓柱所受到的阻力;ρ為流體密度;Uinlet為進口速度。

將本文數(shù)值模擬得到的Cl、Cd及St與文獻數(shù)據(jù)進行對比,結(jié)果如表1所示。可以看出,本文數(shù)值模擬結(jié)果與文獻結(jié)果吻合較好,本文所采用的數(shù)值方法的準確性得到了驗證。

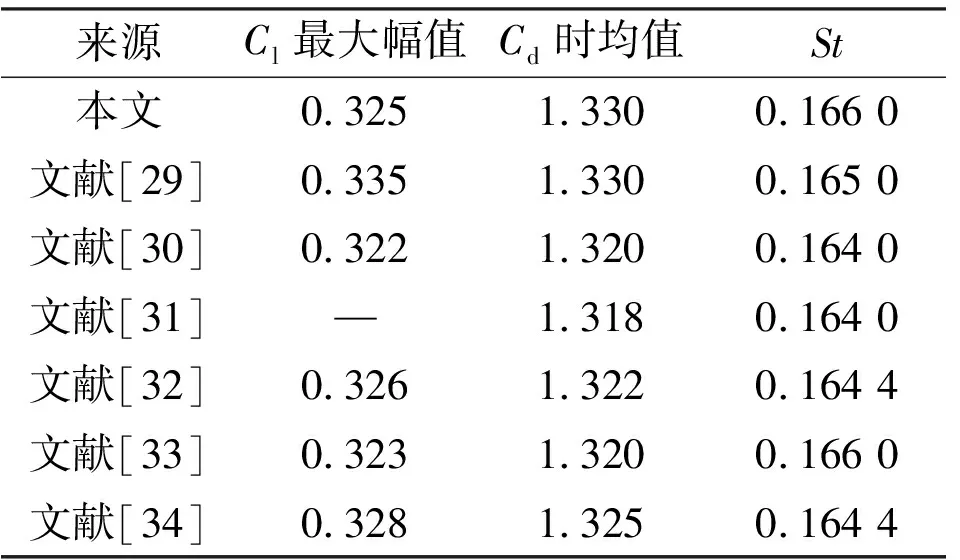
表1 升、阻力系數(shù)及St與文獻數(shù)據(jù)對比

3 結(jié)果與討論

對周期性流場中1 000個流場快照進行POD,并分別構(gòu)建4、6、8階流場降階模型。不同階數(shù)下的預(yù)測前兩階POD模態(tài)時間系數(shù)(a1、a2)及預(yù)測系數(shù)a1與POD的絕對誤差如圖5所示。

(a)a1

(b)a2

(c)a1與POD的絕對誤差

從圖5可以看出,起初隨著階數(shù)增大,各階模態(tài)時間系數(shù)的預(yù)測精度逐漸提高。但是,提高至8階后,誤差反而有所增大。這是由于構(gòu)建的動力學(xué)系統(tǒng)中,微分方程中多項式系數(shù)由模態(tài)投影得到。由于對空間進行離散,數(shù)值誤差隨著多項式系數(shù)矩陣大小不斷增加,數(shù)值誤差積累超過了提高階數(shù)帶來的改進,因此不斷提高降階模型的階數(shù)并不能使得精度一直增大。此外,對比誤差隨時間變化的趨勢可以看出,對于2、4階的降階模型,模態(tài)時間系數(shù)隨時間逐漸增大,有無限發(fā)散的趨勢,且由于預(yù)測周期與實際周期有差別,導(dǎo)致相位誤差逐漸累積。對于6、8階的降階模型,模態(tài)時間系數(shù)沒有逐漸增大,但是相位誤差同樣在不斷累計,這都導(dǎo)致了誤差隨時間不斷增大。

分別以2、4、6、8階模型為基準,對POD模態(tài)時間系數(shù)進行修正,LSTM神經(jīng)網(wǎng)絡(luò)的參數(shù)如表2所示。

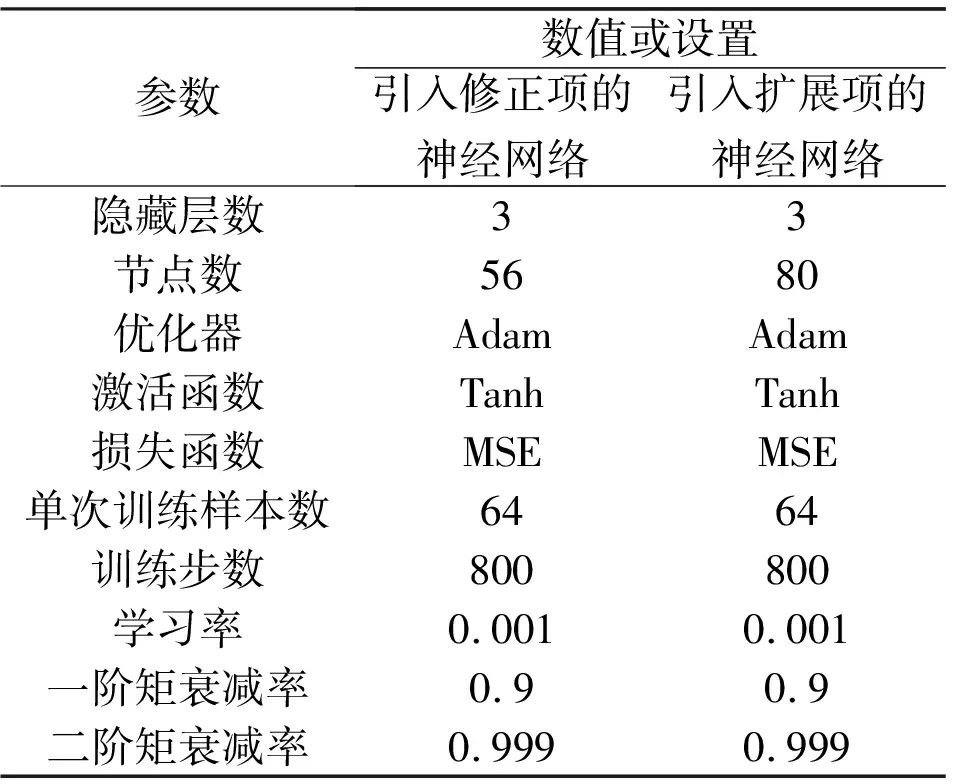
表2 LSTM超參數(shù)列表

將訓(xùn)練好的模型添加到POD-Galerkin降階模型當中,重新進行模態(tài)時間系數(shù)的計算,即可得到通過神經(jīng)網(wǎng)絡(luò)修正的降階模型數(shù)據(jù)。圖6～9展示了4個不同修正模型和原始POD-Galerkin降階模型的前兩階POD模態(tài)時間系數(shù)的對比情況。可以看出,通過神經(jīng)網(wǎng)絡(luò)修正后,降階模型預(yù)測的模態(tài)時間系數(shù)基本與實際值一致,誤差也沒有逐漸增大的趨勢。圖8中,第5階模態(tài)相較其他各階模態(tài)誤差較大。這是由于給定神經(jīng)網(wǎng)絡(luò)訓(xùn)練的均方根誤差目標是使得各階模態(tài)的誤差之和最小,第5階模態(tài)的修正項并未收斂到局部最優(yōu)的修正參數(shù)。

(a)a1

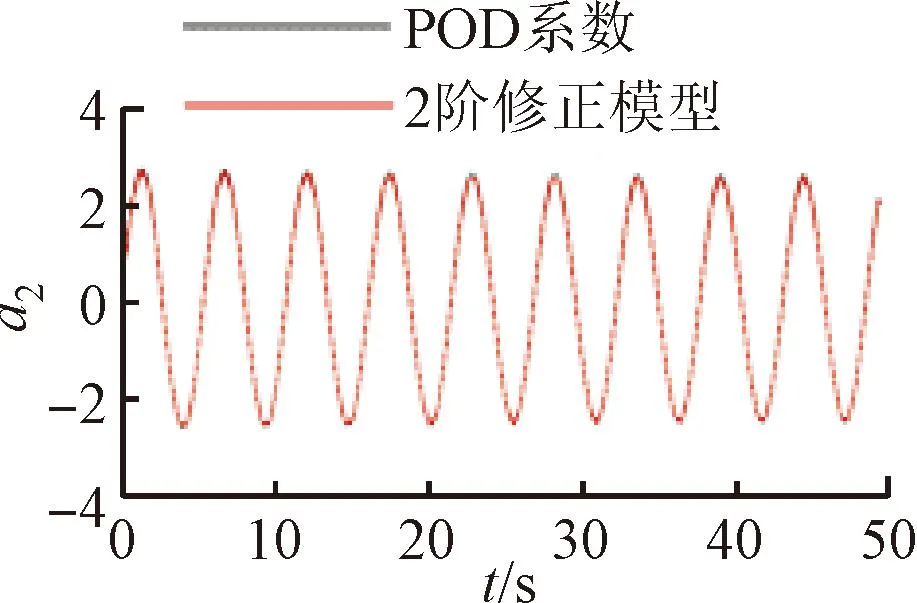
(b)a2

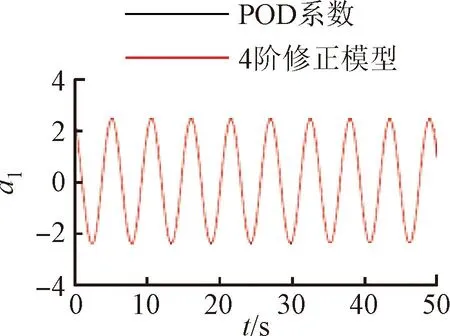
(a)a1

(b)a2

(c)a3

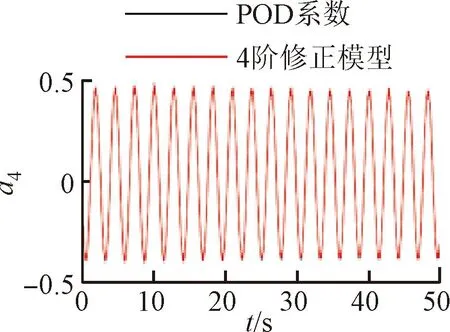
(d)a4

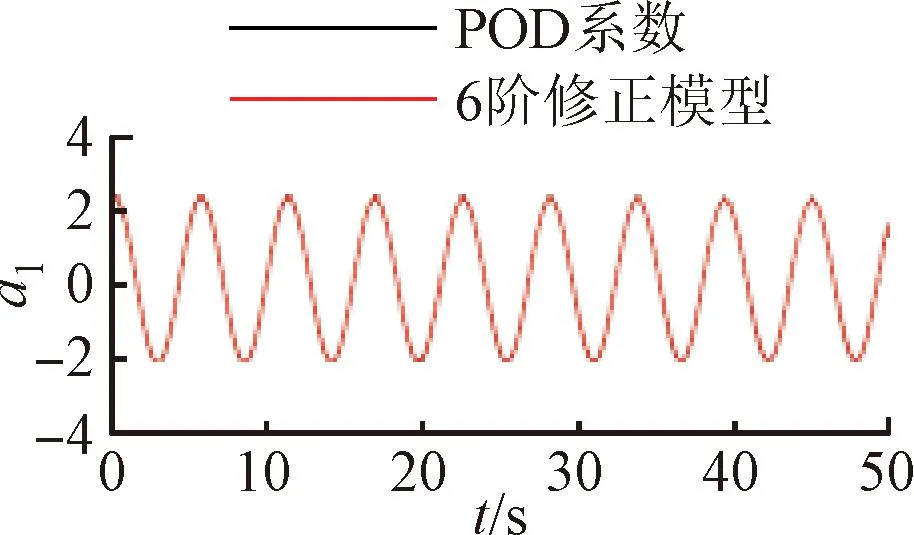
(a)a1

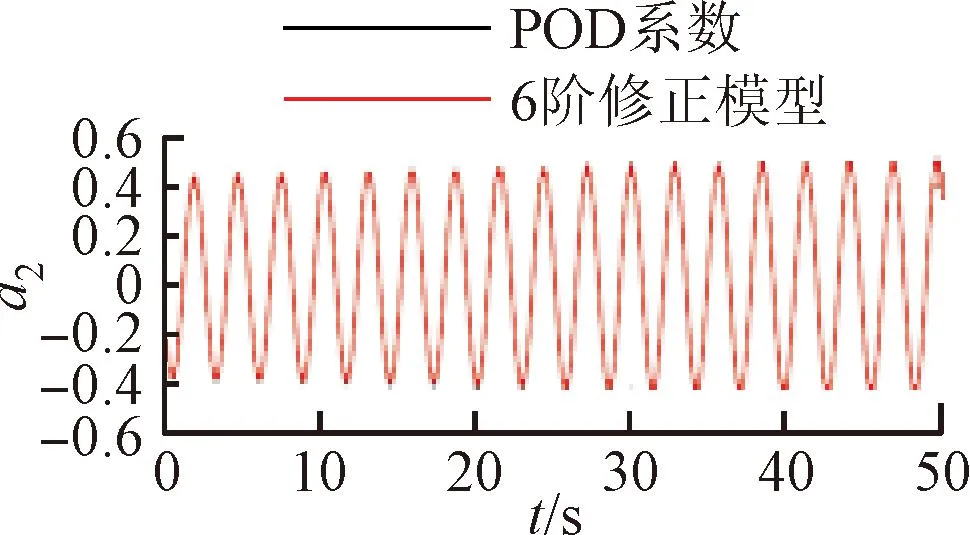
(b)a2

(c)a3

(d)a4

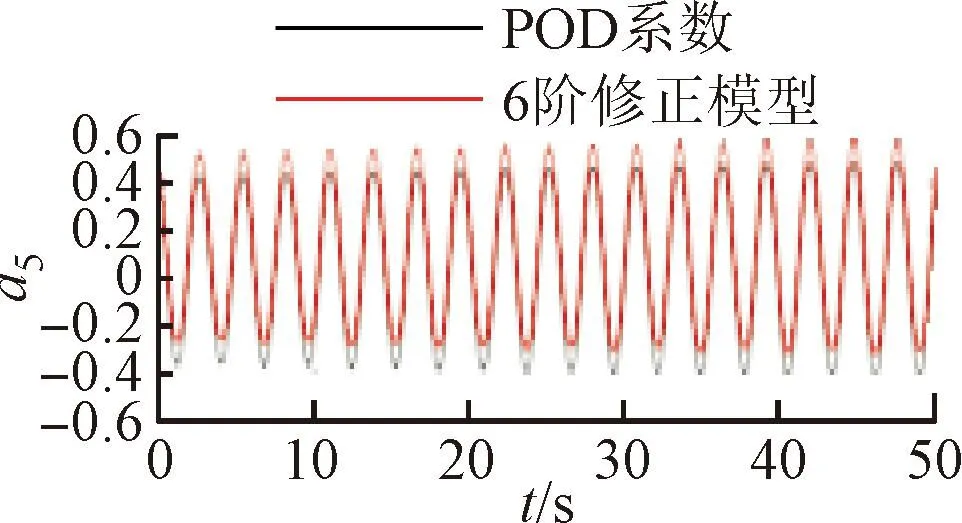
(e)a5

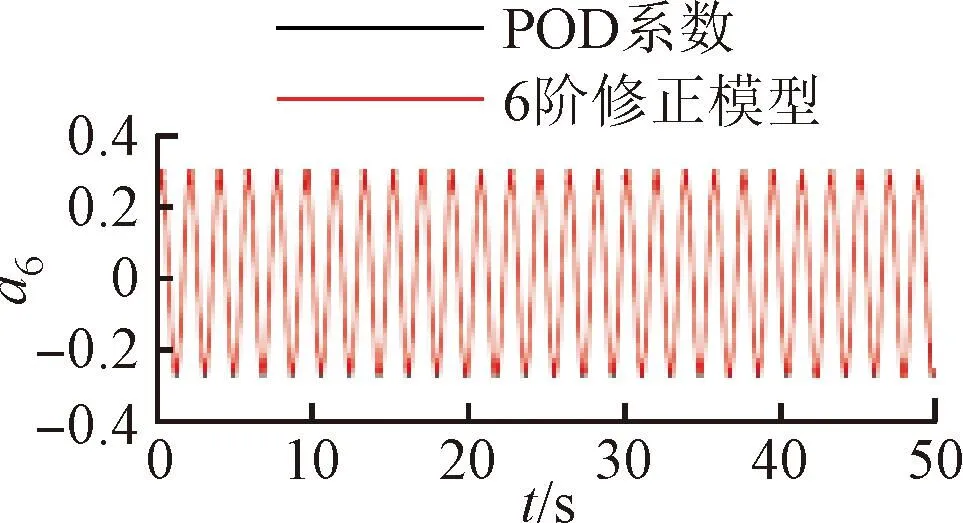
(f)a6

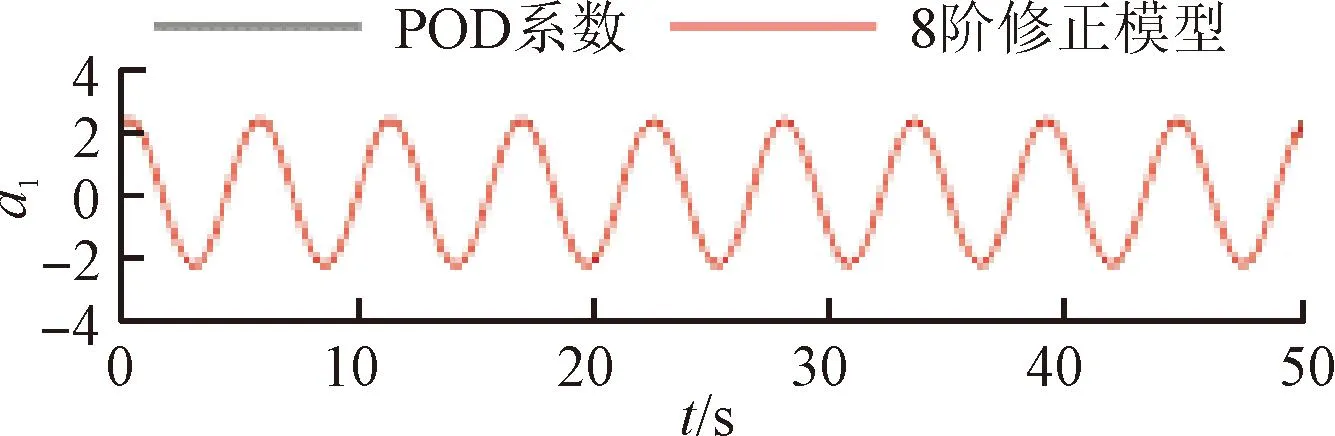
(a)a1

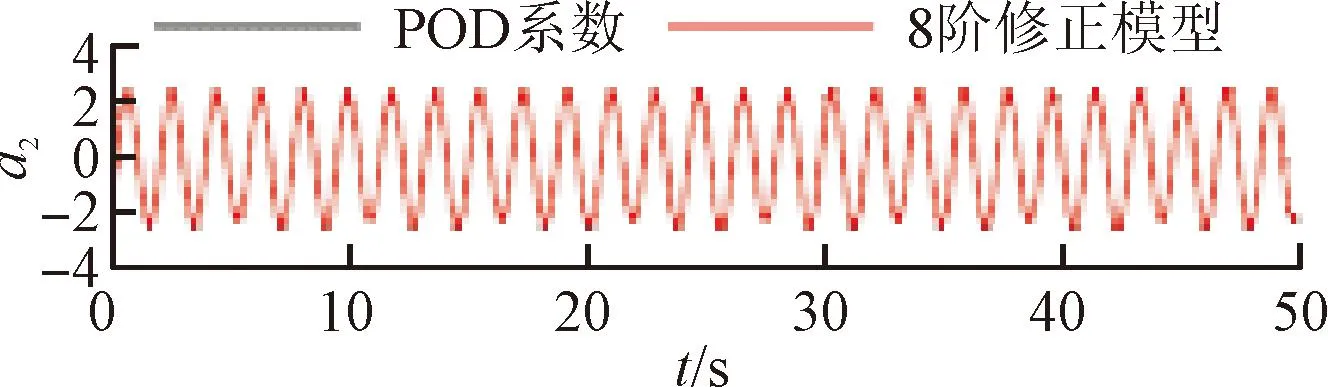
(b)a2

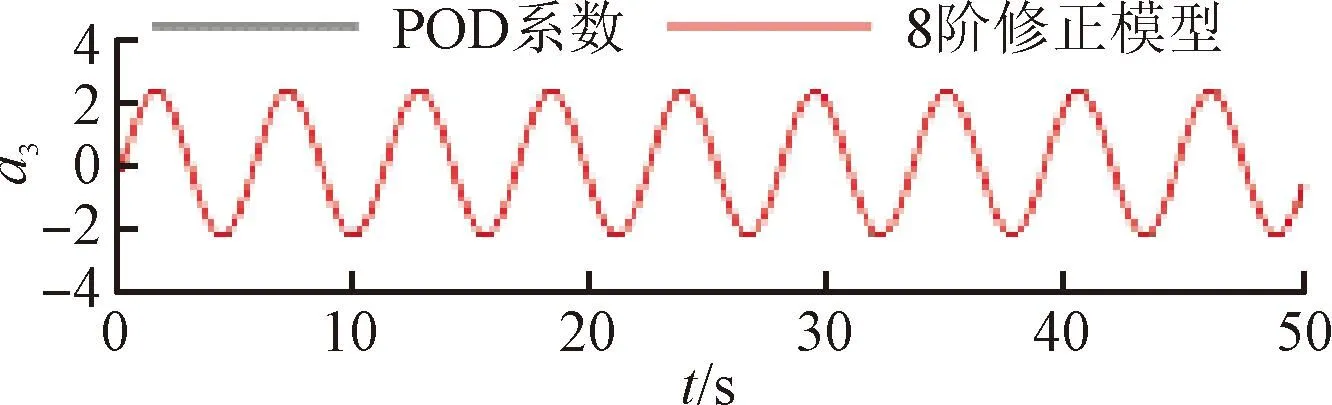
(c)a3

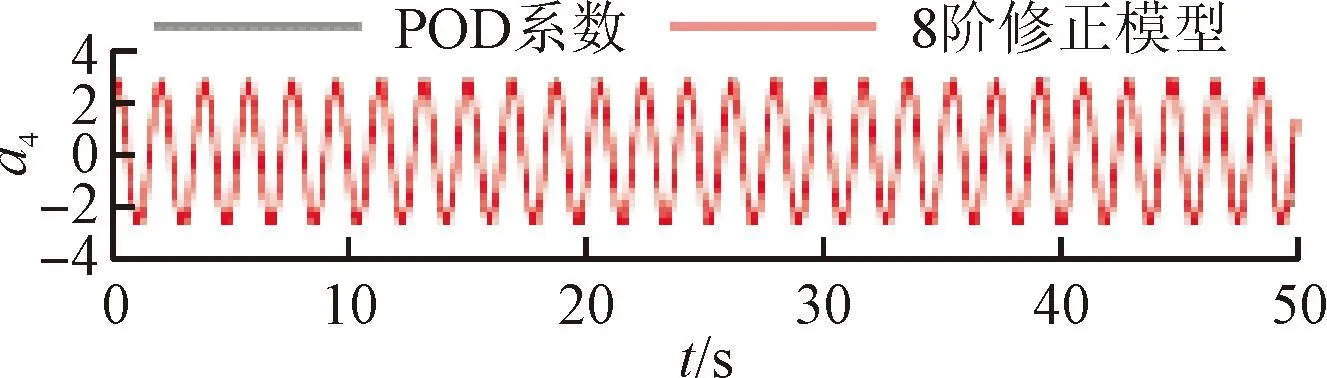
(d)a4

(e)a5

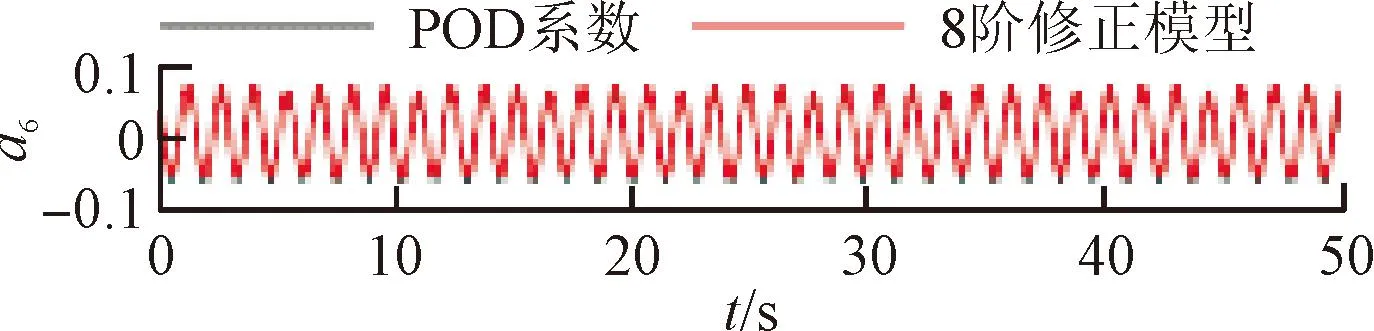
(f)a6

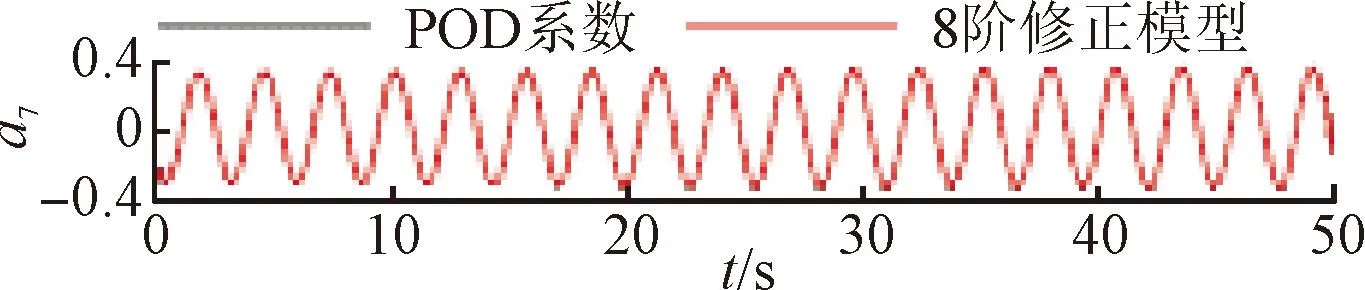
(g)a7

(h)a8

對通過神經(jīng)網(wǎng)絡(luò)修正后的降階模型進行擴展,將2、4、6階降階模型分別擴展至8階。將預(yù)測的高階模態(tài)時間系數(shù)加入流場重構(gòu)當中,不同擴展階數(shù)的改進降階模型預(yù)測流場與原始流場的渦量(經(jīng)過無量綱化處理)對比如圖 10所示。可以看出,將2階模態(tài)擴展至8階,預(yù)測流場誤差較大,而4階模態(tài)擴展與6階模態(tài)擴展至8階幾乎沒有差別,得到的預(yù)測流場與原始流場基本一致。

(a)原始流場

(b)2階擴展

(c)4階擴展

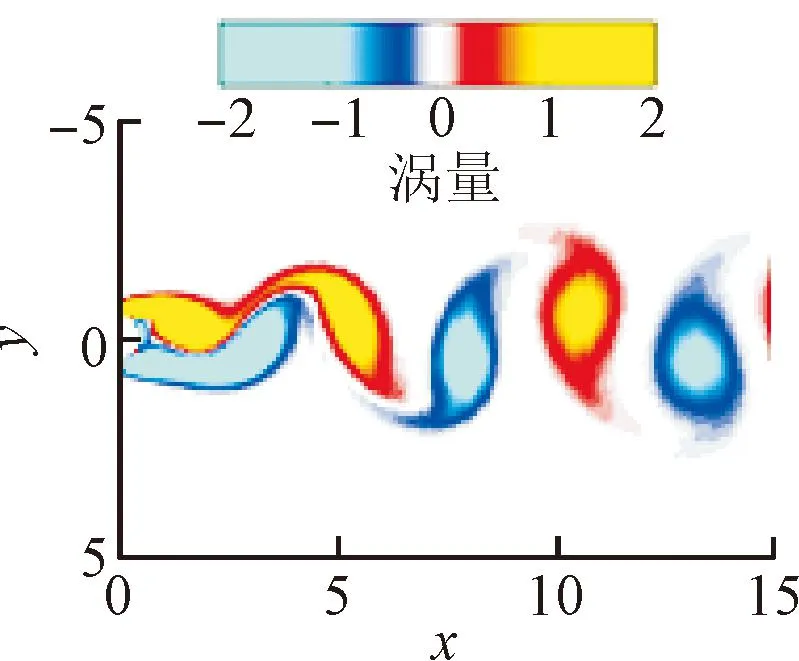
(d)6階擴展

定義各階模態(tài)時間系數(shù)的均方根誤差為

(16)

各階模態(tài)時間系數(shù)均方根誤差如表3所示。各階模態(tài)的時間系數(shù)預(yù)測與原始數(shù)據(jù)相比,POD-Galerkin降階模型在前6階模態(tài)的預(yù)測精度較高,而第7階模態(tài)的時間系數(shù)有較大的相位誤差。改進后模型各階模態(tài)的均方根誤差均較POD-Galerkin降階模型要小1～2個數(shù)量級。相較于引入修正項的神經(jīng)網(wǎng)絡(luò),引入擴展項的神經(jīng)網(wǎng)絡(luò)預(yù)測效果較差,但隨著階數(shù)的增大,引入擴展項神經(jīng)網(wǎng)絡(luò)模型的預(yù)測精度逐漸提高。

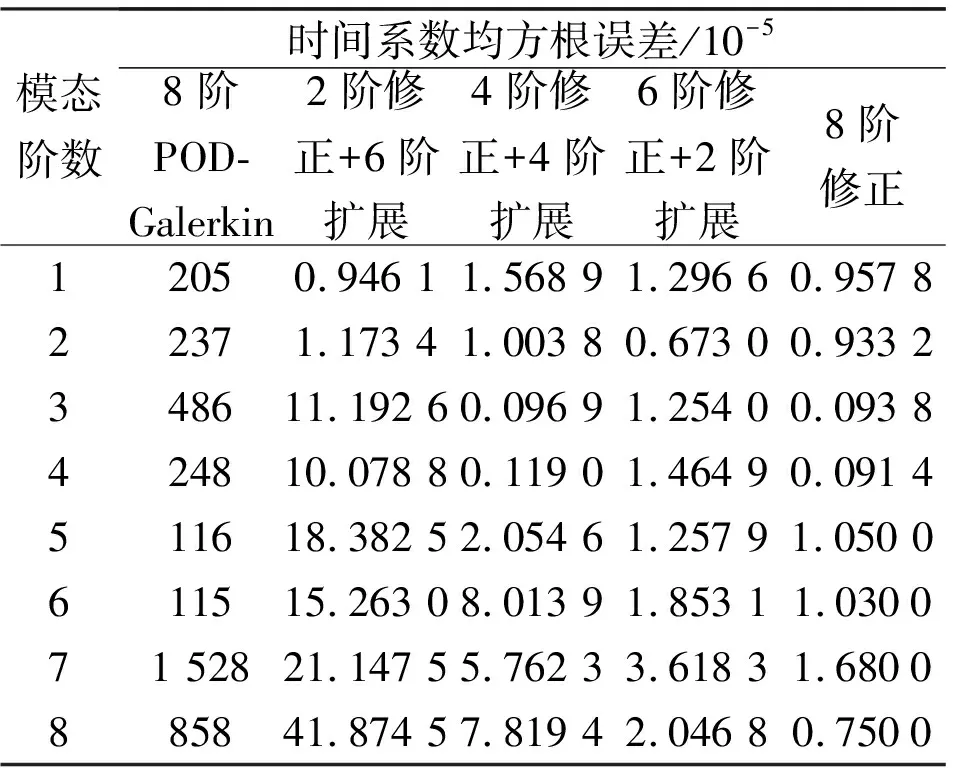
表3 各階模態(tài)時間系數(shù)均方根誤差

表4展示了不同降階模型計算迭代一個時間步耗費的時間。可以看出,標準POD-Galerkin降階模型的計算時間隨模態(tài)階數(shù)的增大而顯著增大。由于改進模型已經(jīng)在訓(xùn)練階段構(gòu)建完成,所以添加不同的改進模型帶來的時間增長近乎一致。4階和6階改進降階模型相較于原始8階POD-Galerkin模型速度分別提高了約56%和25%。

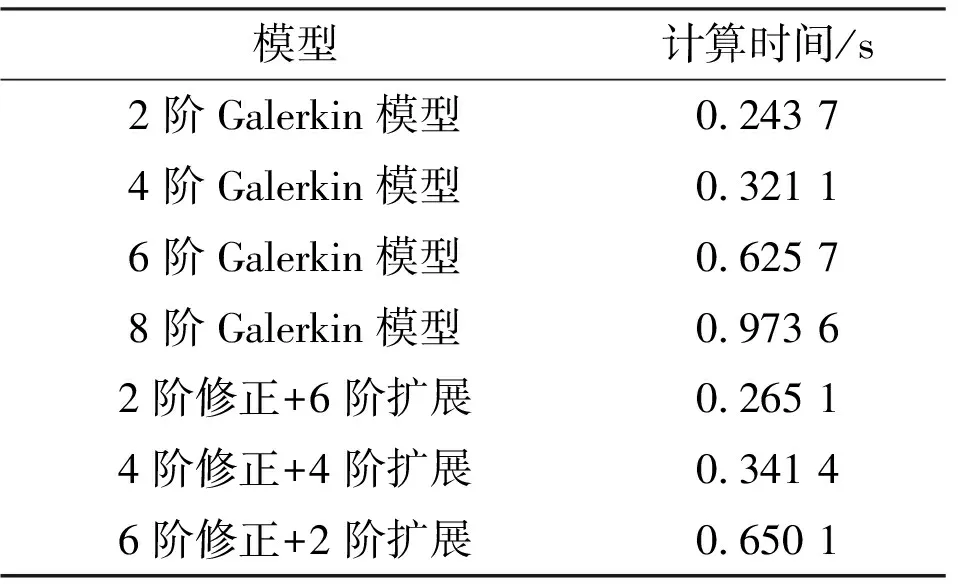
表4 不同模型計算時間對比

4 結(jié) 論

本文利用兩個長短期記憶神經(jīng)網(wǎng)絡(luò)建立了從POD-Galerkin降階模型到實際POD模態(tài)時間系數(shù)之間的修正映射以及低階模態(tài)時間系數(shù)與高階模態(tài)時間系數(shù)之間的擴展映射,通過修正映射和擴展映射分別消除標準POD-Galerkin降階模型誤差累積和擴展降階模型階數(shù),構(gòu)建了改進的POD-Galerkin降階模型。將改進模型應(yīng)用于二維圓柱繞流的流場預(yù)測,對模型的精度和計算時間進行了對比分析。本文主要研究結(jié)論如下。

(1)改進的POD-Galerkin降階模型是數(shù)據(jù)驅(qū)動和物理驅(qū)動的混合模型,其在保留侵入式降階模型的物理背景及可解釋性的情況下,利用長短期記憶神經(jīng)網(wǎng)進行修正和擴展,通過Galerkin投影框架、LSTM修正和LSTM擴展共3個層次準確描述流場變化。

(2)添加長短期記憶神經(jīng)網(wǎng)絡(luò)修正后的降階模型與標準POD-Galerkin降階模型相比更為準確。在相同階數(shù)的降階模型中,修正后的降階模型更貼近實際POD結(jié)果,修正后模型各階模態(tài)的均方根誤差均較標準POD-Galerkin降階模型要小1～2個數(shù)量級。

(3)添加長短期記憶神經(jīng)網(wǎng)絡(luò)擴展項后的改進降階模型在與高階POD-Galerkin降階模型預(yù)測精度相近的情況下,改進降階模型的計算時間要顯著小于原始相同階數(shù)的標準POD-Galerkin降階模型。在精度基本不變的情況下,4階和6階改進降階模型的計算速度相較于8階標準POD-Galerkin降階模型分別提高了約56%和25%。