含固氧顆粒的液氫傳輸管路中靜電積聚仿真研究

田雪皓,劉柏文,王磊,馬原,厲彥忠,雷剛,陳強

(1. 西安交通大學制冷與低溫工程系,710049,西安;2. 航天低溫推進劑技術國家重點實驗室,100028,北京)

液氫具有高比沖、無污染等特點,在航天和能源領域的應用日益廣泛[1]。但是,液氫易燃易爆且高度電絕緣,在輸送過程中易產生靜電起電,造成安全隱患[2]。同時,液氫作為深冷介質,其工作溫度遠低于空氣凝固點。在進行液氫加注、排空等操作時,空氣易滲入并形成固空顆粒[3]。由于氮在液氫中的溶解度更高,積累的固空多為富氧或固氧顆粒[4-5]。固體顆粒與管壁碰撞產生靜電電荷,即摩擦荷電。當電荷累積到一定程度時,可能導致火花放電引發爆炸[6-7],若固空顆粒中氧比例較高,甚至可能發生爆轟[8-9]。因此,明確固空顆粒在液氫管流中的靜電積聚規律與邊界對液氫輸送系統的靜電防護尤為重要。

目前,液氫的靜電特性已引起學者關注。Cassutt等[10]通過實驗證明了液氫在儲存和輸運中會產生顯著的靜電積聚,且液氫極低的電導率導致電荷難以耗散。Liu等[11]建立了電場與流場耦合理論模型,仿真得到液氫中電荷密度約為10-12C·m-3。攜帶固空顆粒的液氫管流中,固液兩相流動特性對研究靜電積聚具有重要影響。目前,固-液兩相流的研究對象包括工業領域的管道流、流化床等,常用數值方法有連續法和離散法[12]。其中,連續法較典型的為雙流體模型,而離散法則包括拉格朗日顆粒軌道(Lagrangian particle tracking, LPT)方法和離散單元法(discrete element method, DEM)[12]。在研究稀疏顆粒的運動,即顆粒相體積分數小于5%時,多采用LPT方法[12]。在處理密相顆粒運動時,通常采用DEM方法。Tsuji等[13]利用LPT法對提升管內顆粒的聚團行為進行了研究,并與Tsuo等[14]用雙流體模型得到的結果做了對比,結果表明:兩種模型得到的氣體速度等影響因素對模擬結果的影響趨勢相同,但LPT法得到的結果中顆粒聚團更頻繁,更符合實際過程。上述方法對相間耦合作用和顆粒間作用均有相關描述,但要實現對顆粒荷電的仿真預示仍面臨較大挑戰[15]。

摩擦荷電的本質是兩種不同材料接觸表面電荷的轉移,包括電子、離子和材料轉移等[16]。對于氣力輸送過程中的顆粒荷電問題,Harper[17]指明,因材料功函數的不同而產生的接觸電勢差是電荷轉移的驅動力。Murata[18]、Mehrani等[19]提出了光電發射、表面態等不同的荷電機理。但是,在顆粒碰撞與分離過程中,電荷傳遞微觀過程與荷電機理仍不明確。電子轉移機制認為,金屬間的接觸荷電理論與費米能級和功函數相關,電子通過量子力學的隧道效應進行轉移,金屬-絕緣體的荷電理論與絕緣材料的等效功函數有關,但絕緣體間的荷電理論尚無定論。離子和材料轉移機制分別認為,物質表面水分子層中的離子和物體碰撞摩擦造成的表面磨損導致了電荷交換[16,20]。根據電荷交換載體不同,所建立的荷電模型包括:電容器模型[16],外加電場下的電荷轉移模型[21],水合離子電荷轉移模型[22]和表面狀態模型等[16]。微觀尺度的研究有助于揭示電荷的內在轉移規律,完善顆粒荷電機理,而宏觀尺度的研究對顆粒流動帶電行為的監測和控制具有價值。兩相流動中顆粒群的電荷積聚過程并非單顆粒碰撞的簡單疊加,流場不僅起到動力源作用,也通過雙向耦合影響顆粒行為,使顆粒群的荷電過程更為復雜。在實驗層面,Watano[23]發現,隨著輸送氣流速度增加,顆粒電荷在達到飽和前會持續增加,而Nifuku等[24]的結果顯示,顆粒比電荷(單位質量顆粒帶電量)隨流速增加存在極值。實驗結果的不可重復性歸因于顆粒電荷對環境因素的敏感性,實驗初始和邊界條件難以控制。在理論層面,Tanoue等[25]的結果顯示,顆粒電荷隨Re增加而減少,但Grosshans等[26]的結論與之相反,說明不同荷電模型對應的電荷交換載體對荷電過程的影響不同。Lim等[27]發現,靜電力對顆粒行為的影響不大,而Grosshans等[28]的研究表明,靜電力主導顆粒的渦旋運動。Li等[29]的結果顯示,St數高的顆粒更易受到靜電的影響。理論計算結果同樣不具備廣泛的一致性,這是因為單個荷電模型無法涵蓋所有作為電荷交換的載體,潛在的荷電機理仍沒有被完全揭示。其中,由電容器模型得到的理論數據與實驗的驗證性較好,也被多數學者采納。

兩相流動電荷積聚研究中,對于液氫這種低黏度、低密度、低電導率的低溫流體研究較少,固氧/固空顆粒等低溫物質的電學性質難以測量,而液氫加注工藝流程的靜電防護對運行安全性尤為重要。因此,研究低溫液氫中固氧顆粒在輸送過程中產生靜電的積聚效應及分布特點,建立靜電積聚的數理模型,并獲得定量的積聚規律特性,為提出抑制或消除管內顆粒靜電積聚的方法和措施提供理論依據,減小由于顆粒輸運過程中靜電積聚產生的危險性,對于控制監測顆粒電荷積聚具有重要指導作用。本文研究湍流、顆粒和管道間復雜的相互作用及液氫管路靜電積聚規律與邊界,通過參數化研究分析固氧顆粒電荷演化過程的積累效應以及電荷積聚的影響因素和分布規律。

1 數值模型建立

本文建立了拉格朗日顆粒軌道法與計算流體動力學(computational fluid dynamics, CFD)的耦合模型,并采用電容器模型對液氫管路中固氧顆粒的起電過程開展仿真研究。含固氧顆粒的液氫管內固液兩相流物理模型示意圖如圖1所示。其中,水平傳輸管長為L,半徑為R,液氫攜帶固氧顆粒以流速uinlet流入,從右側排出。固氧顆粒速度為up,帶電量為Q。

圖1 含固氧顆粒的液氫管流示意 Fig.1 Schematic diagram of liquid hydrogen pipe flow with solid oxygen particles

1.1 流體-顆粒動力學模型

將液氫視為不可壓連續介質。在歐拉坐標系框架下,采用Navier-Stokes方程描述液氫流動過程,并通過相間相互作用與顆粒相耦合。由于液氫管路中滲入空氣量較少,固氧顆粒量較少[5],顆粒體積分數與流體相比可忽略,因此在控制方程中不引入顆粒相體積分數。流體質量和動量方程表示為

(1)

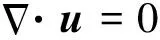
(2)

式中:u、p、ρ、ν、Fs分別為流體速度、壓力、密度、運動黏度和顆粒對流體體積力。

假設顆粒由相同材料、剛性、單分散、單組分的稀疏球形顆粒組成,選用LPT法對固液兩相流開展仿真[12]。其中,每一個固氧顆粒均可被示為一個質點,運動方程通過牛頓第二定律[30]得出

(3)

式中:fg、fcoll分別表示由重力和碰撞引起的加速度;∑fp包括顆粒所受曳力、浮力、靜電力、壓力梯度力、虛擬質量力、Saffman力、Basset力等引起的加速度,但與顆粒本身慣性相比,靜電力、Basset力對顆粒行為的影響很小,通常可以忽略[30]。

單個固氧顆粒所受曳力[26]為

(4)

式中:Cd為曳力系數;urel表示滑移速度。曳力系數與顆粒雷諾數Rep=2|urel|rp/ν的關系[26](rp為顆粒半徑)如下

(5)

顆粒間碰撞為完全彈性碰撞,不考慮碰撞造成的速度、能量損失。顆粒與壁面間是不完全彈性碰撞,碰撞后顆粒法向速度改變

u′p,n=-keup,n

(6)

式中:ke為恢復系數。

1.2 顆粒荷電模型

對于金屬-絕緣體碰撞,通常采用電容器模型[16]。該模型假設電子轉移是電荷交換的主要方式,并將顆粒與壁面的接觸區視為電容器,如圖2所示。

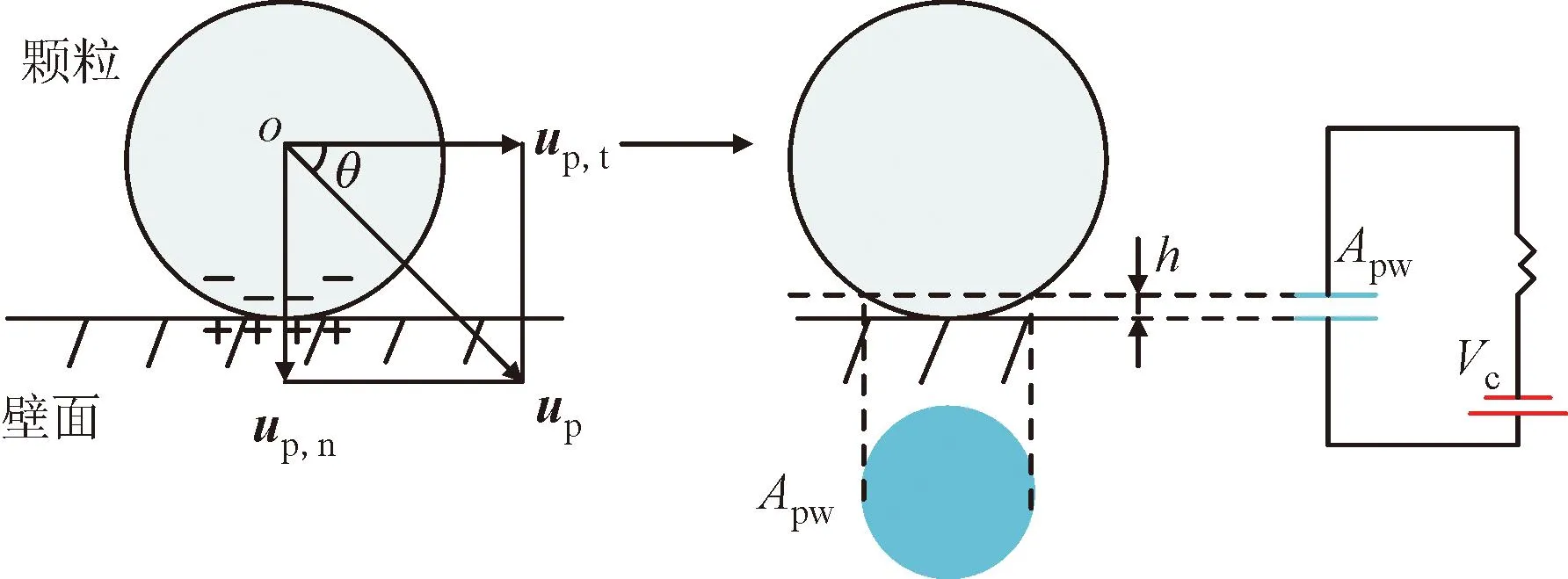
圖2 粒壁碰撞示意Fig.2 Schematic diagram of particle-wall collision

電容器模型采用接觸體表面功函數差Vc驅動電子轉移,與接觸體幾何因素相關的電容間隙h由電子轉移的臨界距離決定,接觸面積Apw用于計算電荷交換面積以及接觸電容。顆粒與壁面分離后,得到電子的顆粒帶負電,交換的電荷從碰撞區域均勻擴散至整個顆粒表面。液氫管路中固氧顆粒與管壁的碰撞視為金屬-絕緣體碰撞,并且液氫系統溫度恒定為20 K,溫度對材料物性及電荷交換的影響可忽略[16]。因此,本文可采用電容器模型計算兩相流中顆粒的電荷積聚。

固液兩相輸送過程發生兩類電荷交換,包括顆粒間碰撞引起的電荷擴散和顆粒-壁面碰撞引發的電荷轉移。顆粒i和顆粒j接觸期間,各自電荷交換量ΔQi和ΔQj[26]為

(7)

式中:Ci、Cj、τpp、Δtpp分別為顆粒i、j的電容、顆粒電荷弛豫時間和接觸時間,可按照下列公式確定

Ci=4πε0rp,i

(8)

(9)

(10)

(11)

αij=

(12)

其中,ε0為真空介電常數,Aij為顆粒接觸面積,φp為顆粒電阻率,up,ij為顆粒間相對速度,αij為顆粒接觸系數,vp和Ep分別表示顆粒泊松比和楊氏模量。

有別于顆粒間碰撞,顆粒與壁面碰撞的電荷交換量ΔQpw由動態電荷轉移ΔQc和預電荷貢獻ΔQt組成[26,31],ΔQc和ΔQt分別與材料和顆粒電荷有關。ΔQpw的定義為

ΔQpw=ΔQc+ΔQt

(13)

ΔQc=CVc(1-e-Δtpw/τpw)

(14)

(15)

式中:C、Vc、Δtpw、τpw和αpw分別為接觸電容、接觸電位差、粒壁接觸時間、電荷弛豫時間和碰撞系數,可按照下列公式確定

(16)

(17)

τpw=εε0φp

(18)

(19)

Apw=πrpαpw

(20)

其中,Apw為接觸面積,vw和Ew分別為壁面泊松比和楊氏模量,ε為壁面相對介電常數。

顆粒間相互碰撞不會產生新的電荷,僅會交換原有電荷;顆粒與壁面碰撞產生新的電荷,并且由于顆粒-流體、流體-壁面之間的電荷交換可忽略,粒-壁碰撞也是固液兩相流中顆粒帶電的唯一來源[32]。

粒壁間電荷交換由不同材料間的接觸電位差Vc驅動[16],其表達式為

(21)

式中:Vp、Vw分別為顆粒和壁面材料的表面功函數,等號右側第3項表示由顆粒荷電后引起的附加電勢差。

顆粒和壁面材料的功函數決定了電荷積聚程度。功函數是將電子從固體內部轉移到表面外一點所需的最小能量。對于固氧顆粒,可利用Materials Studio軟件計算其物性。本文通過比較固氧晶體費米能級與遠離晶體表面的靜電勢計算固氧功函數。由于固氧凝固后隨溫度降低形成不同的晶體結構,導致晶格參數(a～Vm)發生改變,本文根據表1數據構建20 K液氫系統中固氧α-O2晶胞[33]。由于功函數對晶體結構和表面取向具有較大依賴性,首先需要依據能量守恒對固氧晶胞進行分子、幾何優化以忽略晶體表面松弛的影響。隨后,切割晶胞形成單面分子層并構建間隔20×10-10m真空層的堆積陣列,以忽略真空層兩側分子層的靜電相互作用。最后,根據堆積體系靜電勢的空間分布可得到固氧α-O2的功函數約6.37 eV。此外,本文通過上述方法得到金屬鉻Cr的功函數為4.46 eV,與標準值(4.5 eV)的誤差不到1%。因此,該方法能夠準確計算材料功函數。

表1 20 K下固氧α-O2的晶胞結構[33]

1.3 模型設置

本文取管長為2 m、管徑為10 mm的水平管為參考工況,研究含固氧顆粒液氫管流的靜電積聚規律。采用COMSOL Multiphysics軟件建立水平管三維模型。設置速度入口、壓力出口,無滑移壁面邊界條件,管壁接地以導出壁面電荷,該處理不影響顆粒電荷積聚飽和值。顆粒以與流體相同速度注入,顆粒數由顆粒質量確定。

在固液兩相流模擬中,時間步長Δtp通常取Rayleigh時間步長ΔtR的10%～40%以滿足精度要求[34]。本文采用Rayleigh時間步長的30%,即8×10-7s進行仿真計算。其中,Rayleigh時間步長根據最小顆粒尺寸計算,計算公式為

(22)

式中:Gp為顆粒剪切模量。

1.4 模型驗證

本文建立了網格單元數分別為21萬、84萬、119萬和166萬的4套模型,根據顆粒比電荷Qsc和平均沖擊電荷ΔQpw(電荷交換量)評價網格的適用性,結果如圖3所示。可以看出,采用119萬網格單元模型滿足要求。

圖3 網格數對數值計算結果的影響Fig.3 Influence of grid number on numerical results

圖4給出了單個聚四氟乙烯(PTFE)顆粒與黃銅板碰撞帶電過程預測結果,并與Grosshans等[35]和Matsuyama等[36]的數據進行了比較。圖4(a)顯示了顆粒電荷Q和沖擊電荷ΔQpw的演變過程,平均誤差分別為1.59%、4.76%。圖4(b)顯示了沖擊電荷ΔQpw隨顆粒初始電荷的變化規律,計算結果遵循Matsuyama等[36]提出的線性曲線,與實驗數據的平均誤差為13.18%。

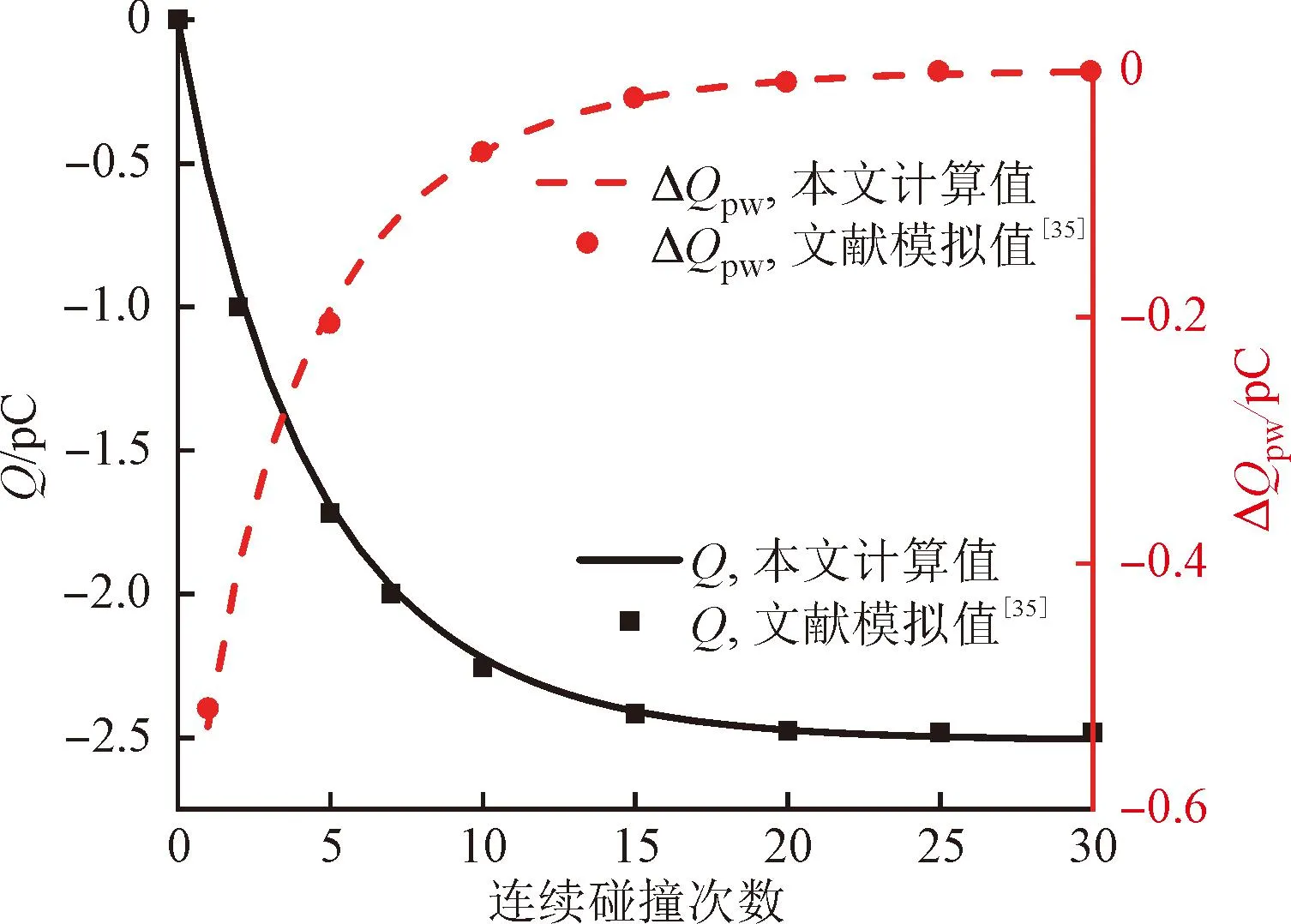
(a)顆粒電荷和沖擊電荷的演變過程

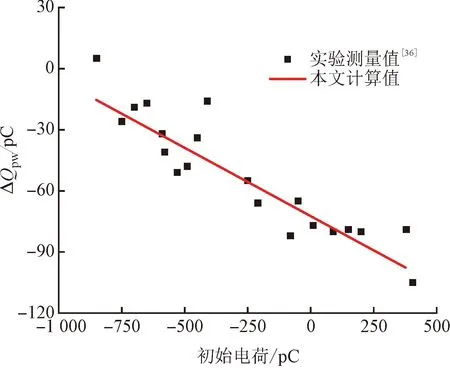
(b)初始電荷對沖擊電荷的影響

針對固液兩相流電荷積聚,本文選用Watano[23]數據作為比較依據,結果如圖5所示,研究對象為氣力輸運水平管道中2.5 g聚甲基丙烯酸甲酯(PMMA)顆粒的電荷積聚過程,顆粒帶負電。可以看出,顆粒比電荷Qsc隨Re增加存在極大值。數據平均誤差為7.22%,最大誤差為18.40%。綜合來看,本文所構建模型能夠表征固氧顆粒的電荷積聚規律。

圖5 顆粒比電荷隨雷諾數的變化規律Fig.5 Variation of particle specific charge with Re

2 結果與討論

本文模擬流體相為液氫、固體相為α-O2的固氧顆粒,溫度為20 K。表2提供了用于模擬含稀相固氧顆粒的液氫水平管參數。由于顆粒表面電位極性不確定,本節顆粒電荷以絕對值給出[35]。其次,本研究中顆粒相體積分數最大值為4.9%,小于5%,滿足LPT法的使用條件[12]。

表2 模擬所用的含稀相固氧顆粒的液氫水平管參數

2.1 固液兩相流動電荷積累效應

圖6(a)展示了帶電顆粒在液氫管流中的分布。可以看出,進口處多數顆粒不帶電,經過與壁面碰撞起電和顆粒間電荷交換后,出口處帶電顆粒增多,帶電量增強。圖6(b)展示了不同位置4個徑向截面的顆粒電荷分布,圖中r為顆粒距管道中心軸的距離,R為管道半徑。可以看出,壁面區域顆粒電荷遠高于流動核心區域,并通過顆粒間碰撞向核心區傳遞電荷,且隨著流動距離增加,整體帶電量上升。此外,顆粒電荷隨流動距離增加逐漸達到飽和,近壁區的顆粒由于頻繁的粒壁碰撞率先飽和。由圖6(b)可知,固氧顆粒積聚飽和電荷量約為84 pC。

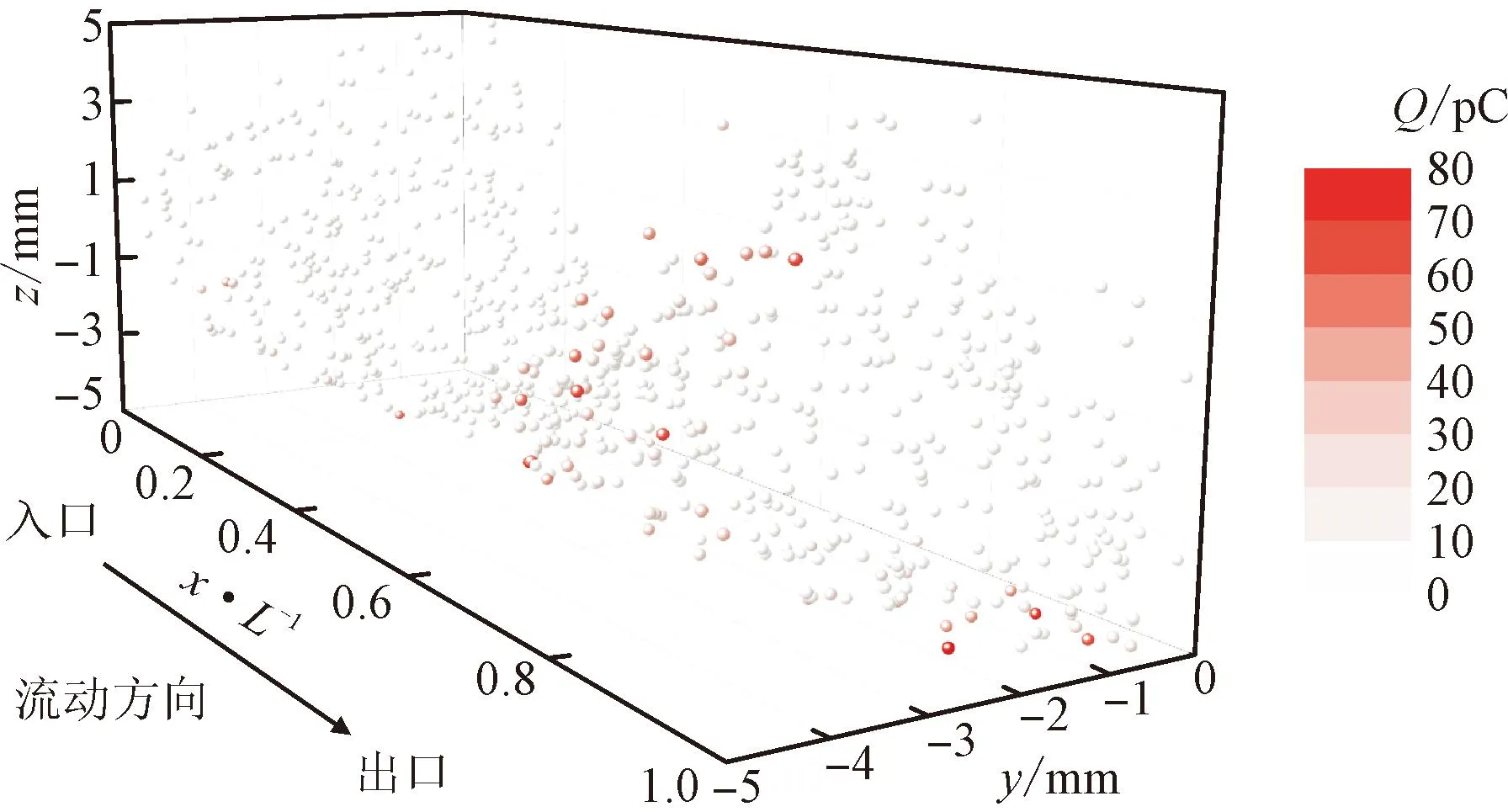
(a)帶電顆粒幾何分布

(b)顆粒電荷隨徑向分布情況

當液氫流速為10 m·s-1時,大部分顆粒攜帶電荷較少,液氫管流中稀相固氧顆粒的平均電荷Qav約為10 pC。將穩態下管內顆粒電量和與管路總體積相比[37]可知,單位體積液氫中固氧顆粒電荷量為2.84×10-4C·m-3,較純液氫大8個數量級[11]。因此,含固氧顆粒液氫管流的靜電防護面臨更嚴峻的挑戰。

靜電電荷隨時間和位移不斷積累[38],當出口顆粒總電荷Qout達到安全閾值時,可能引發靜電危害。圖7展示了不同管長的出口電荷Qout隨時間變化規律。可以看出,出口電荷Qout隨顆粒群的流動逐漸增加并趨于穩定。管道越長,粒壁碰撞次數越多,出口電荷Qout越大,穩定后的出口總電荷Qout分別約為551、1 204、2 233 pC,與管長近似成正比。因此,長管道的安全威脅更大。另外,曲線在入口段的斜率較小,這是由于顆粒釋放后需經歷隨機擴散才能與壁面碰撞。

圖7 不同管長的出口電荷隨時間變化規律Fig.7 The change of outlet charge of different tube lengths with time

2.2 固液兩相電荷積聚影響因素

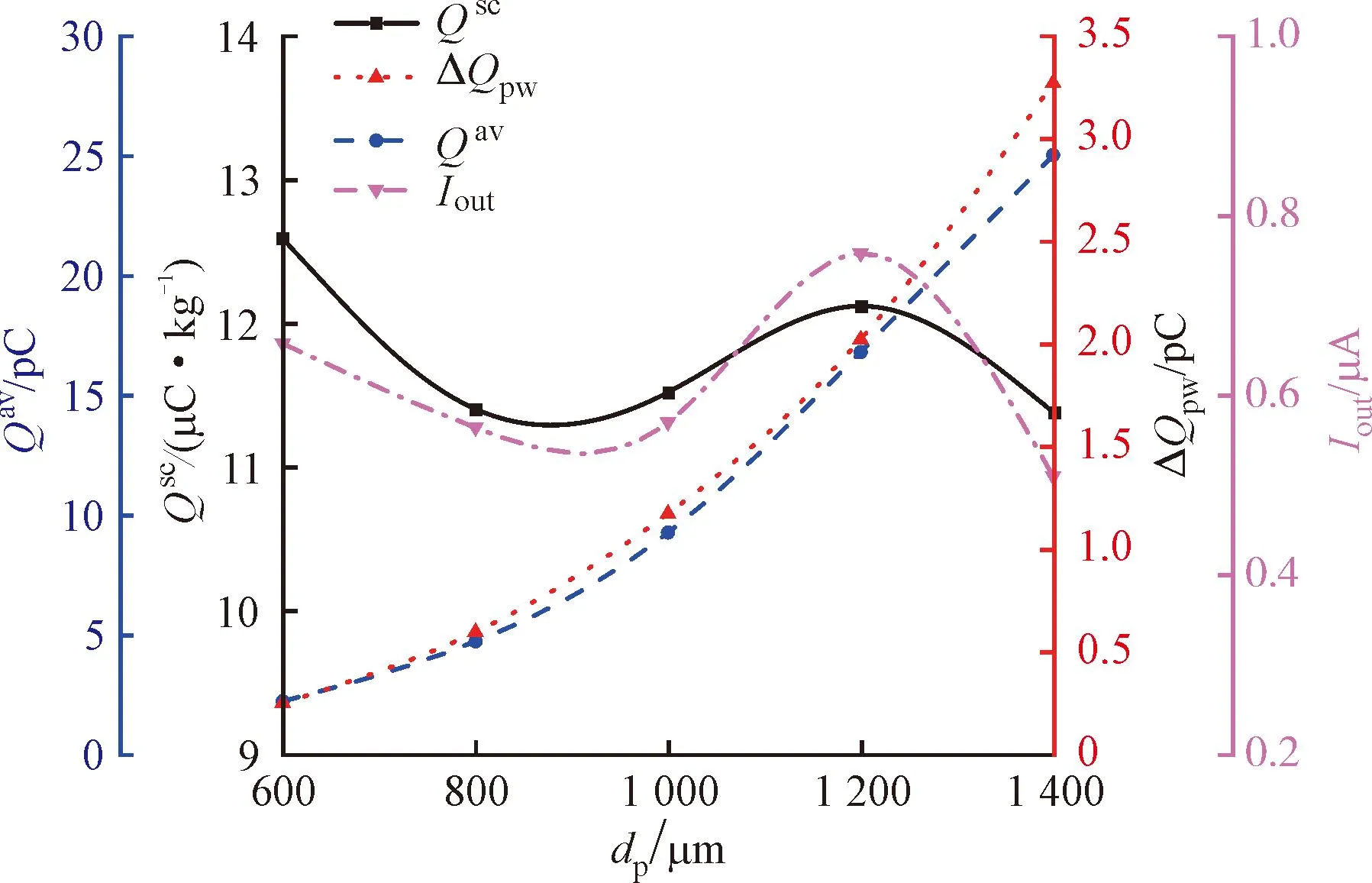
圖8 粒徑對電荷積聚的影響Fig.8 Effect of particle diameter on charge accumulation

圖8顯示了出口比電荷Qsc、平均沖擊電荷ΔQpw、出口粒子平均電荷Qav、出口電流Iout4種統計參數隨固氧粒徑的變化規律。可以看出,隨著粒徑增大,顆粒電荷Qav和沖擊電荷ΔQpw增大,比電荷Qsc和電流Iout存在極小值和極大值。由圖可知,顆粒電荷Qav對粒徑非常敏感,且隨著粒徑增加,顆粒電荷增長趨勢加快。由式(17)、(20)可知,粒徑與接觸面積、時間正相關,故沖擊電荷ΔQpw和顆粒電荷Qav隨粒徑增大而增大。同時,當顆粒質量流量一定時,粒子數隨粒徑增大逐漸減少,所以比電荷Qsc和電流Iout存在極小值和極大值。比電荷Qsc的極小值、極大值分別為11.29、12.12 μC·kg-1,電流Iout的極小值、極大值分別為0.54、0.76 μA。此外,靜電危害通常源于顆粒放電能量過高[39],所以靜電安全性往往由顆粒電荷Qav決定。綜上可知,大尺寸固氧顆粒電荷Qav更大,建議通過布置濾網減小顆粒粒徑的方法提高運行安全性。

圖9展示了沿程沖擊電荷ΔQ(即整個管道內粒壁碰撞所產生的電荷交換)和顆粒出口電荷Q的概率密度函數(probability density function,PDF)。PDF反映了所求數值統計次數與總數的比值。

圖9(a)為沿程沖擊電荷ΔQ的概率密度分布。可以看出,每條曲線均呈現左低右高的趨勢,且粒徑增大,曲線右移。據圖4(a)可知,沖擊電荷隨碰撞次數增多逐漸降低。所以,圖9(a)中每條曲線右側較大的沖擊電荷對應初期碰撞所發生的電荷交換,左側則對應后期碰撞。并且,限于管長,粒壁碰撞大多屬于初期碰撞,故曲線右側PDF更大。同時,粒徑越大,接觸面積、時間越大,沖擊電荷越大,曲線越接近右側。

圖9(b)為出口電荷Q的概率密度分布。可以看出,曲線存在波峰,且粒徑增大,波峰右移,即顆粒電荷Qav增大,與圖8趨勢相符。并且,限于管長,顆粒普遍發生0～20次碰撞,如圖10所示,使得大多顆粒電荷處于相同范圍,故圖9(b)存在波峰。

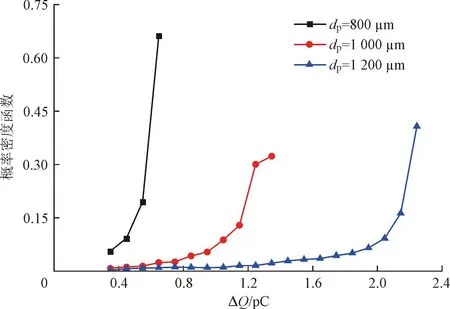
(a)沿程沖擊電荷的概率密度分布

(b)顆粒出口電荷的概率密度分布

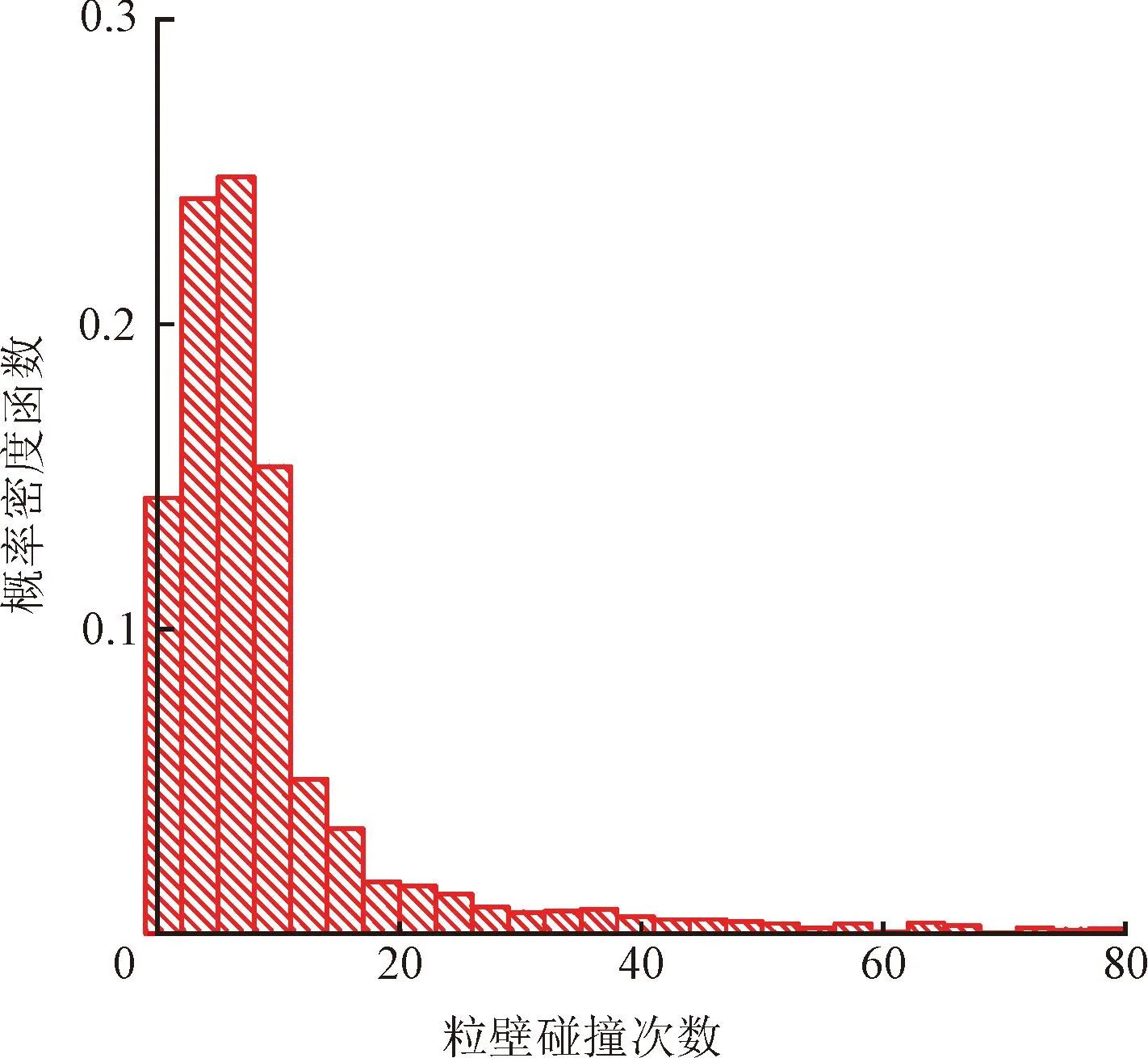
圖10 粒壁碰撞次數直方圖Fig.10 Histogram of the number of grain wall collisions

圖11顯示了4種統計參數隨顆粒質量流量的變化規律。可以看出,隨著顆粒質量流量增加,比電荷Qsc和顆粒電荷Qav略有減小,這是由于粒子數增多導致顆粒間碰撞更頻繁,顆粒軌跡被限制,難以與壁面碰撞。同時,平均沖擊電荷ΔQpw幾乎不變,因為粒子數增加不會影響碰撞劇烈程度。另外,出口電流Iout增加與單位體積粒子數的變化有關。綜上可知,需做好防漏和靜電防護,密切關注固氧顆粒的形成與電荷積聚。

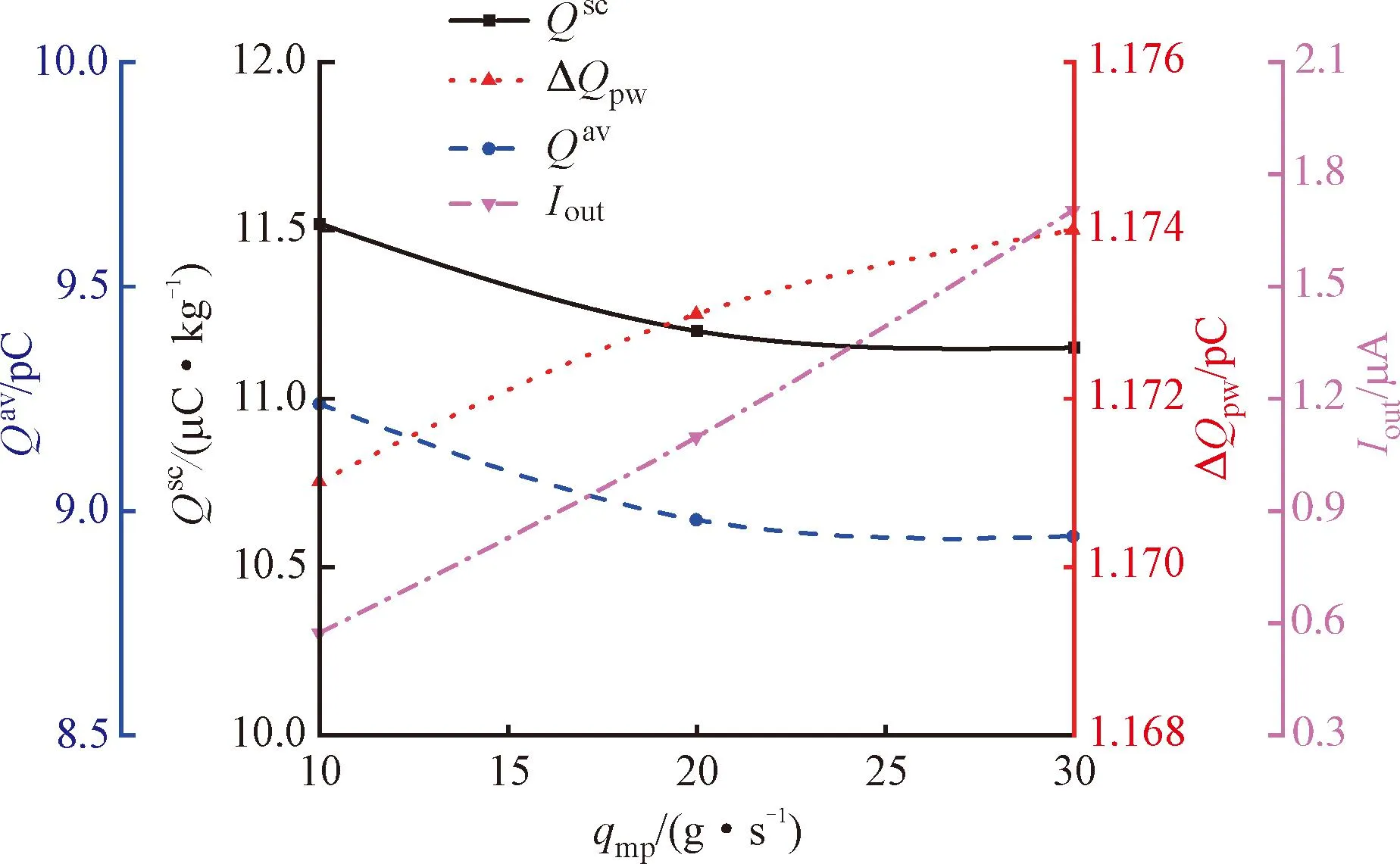
圖11 顆粒質量流量對電荷積聚的影響Fig.11 Effect of particle mass flow on charge accumulation

圖12顯示了4種統計參數隨管長的變化規律。可以看出,隨著管長增加,比電荷Qsc、顆粒電荷Qav和出口電流Iout逐漸增大,且增幅逐漸降低,與圖4(a)趨勢類似。隨著粒壁碰撞次數增多,顆粒電荷逐漸飽和,沖擊電荷ΔQpw降低。因此,長管道電荷積聚更為嚴重。為提高運行安全性,實現降低顆粒電荷Qav的目的,可增設導電銀網、接地線等裝置導出電荷,以降低導電裝置間的管道長度。

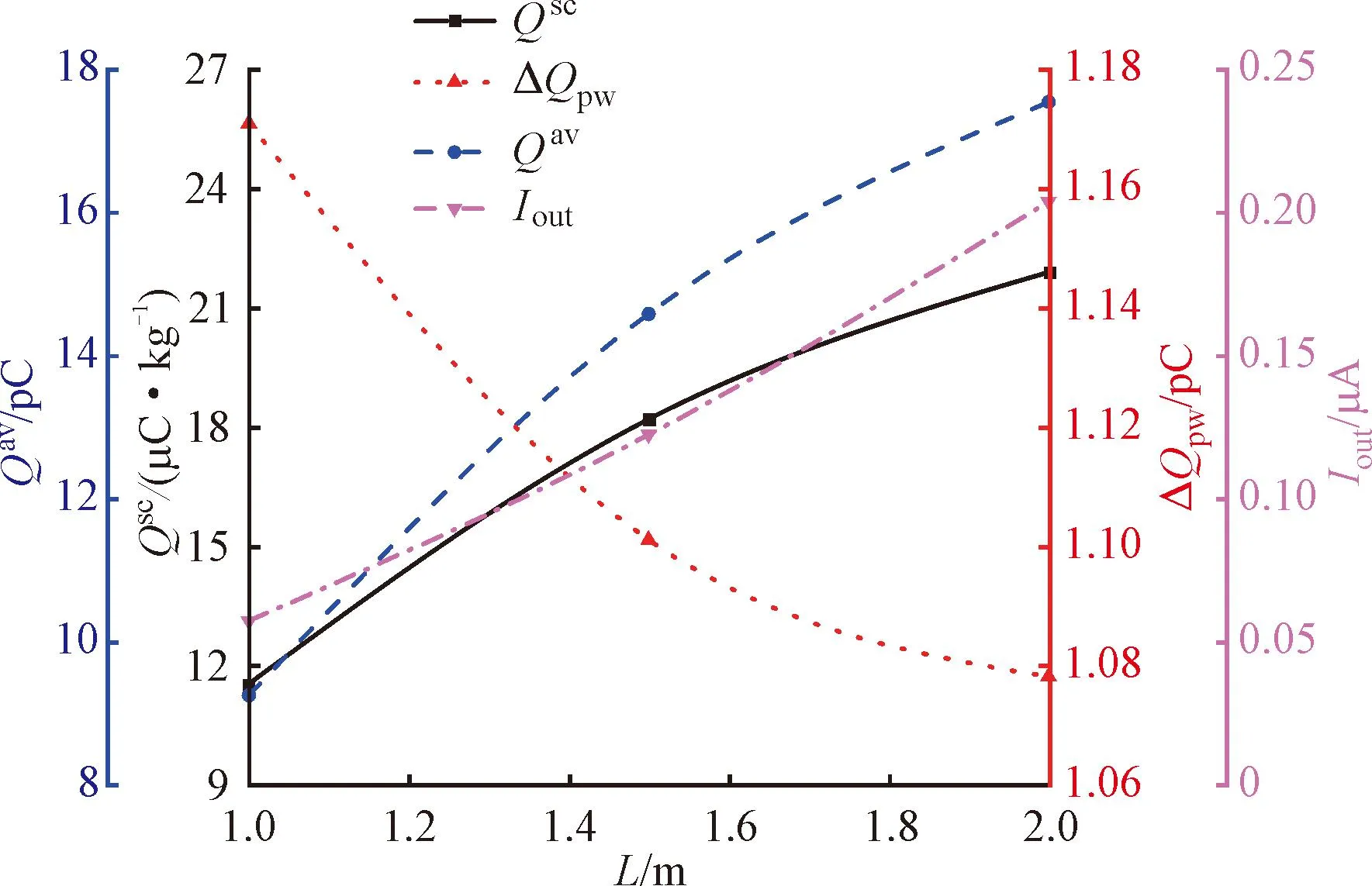
圖12 管長對電荷積聚的影響Fig.12 Effect of tube length on charge accumulation

圖13顯示了4種統計參數隨管徑的變化規律。可以看出,隨著管徑增加,比電荷Qsc、顆粒電荷Qav和出口電流Iout減小,平均沖擊電荷ΔQpw基本不變。根據理論分析可知,隨著管徑增加,顆粒由于重力沉降并與壁面碰撞的速度增大,沖擊電荷隨之增大,但粒壁碰撞概率和電荷交換次數隨之降低。然而,圖13顯示沖擊電荷變化并不大。這是由于本文采用的電容器模型中,沖擊電荷僅取決于顆粒速度。顆粒軸向速度遠大于徑向速度,沉降帶來的影響可忽略。因此,管徑對碰撞速度的影響較小,管徑主要通過碰撞次數影響電荷積聚。

圖13 管徑對電荷積聚的影響Fig.13 Effect of pipe diameter on charge accumulation

圖14顯示了4種統計參數隨流速的變化規律。可以看出,隨著流速增加,比電荷Qsc和顆粒電荷Qav存在極小值,沖擊電荷ΔQpw單調增加,出口電流Iout單調減小。當流速從10 m·s-1增至20 m·s-1時,粒壁碰撞更劇烈,顆粒電荷Qav增加;流速降至5 m·s-1時,顆粒在管道內停留時間和碰撞次數增多,顆粒電荷Qav同樣增加。因此,顆粒電荷Qav和比電荷Qsc隨流速增加存在極小值,分別為9.15 pC、11.41 μC·kg-1。此外,出口電流Iout=nqv0s,其中,n、q、v0、s分別指單位體積粒子數、顆粒電荷、顆粒速度及管道截面積。當顆粒質量流量一定時,隨著流速增加,顆粒群更分散,n值降低,出口電流Iout隨之降低。

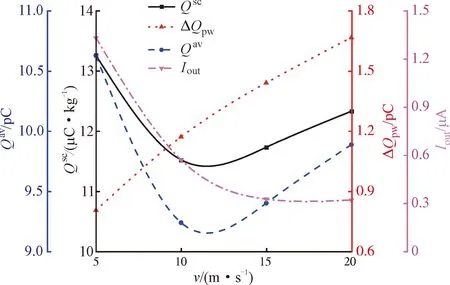
圖14 流速對電荷積聚的影響Fig.14 Effect of velocity on charge accumulation

表3展示了顆粒物性對電荷積聚規律的影響。通過靜電模型可以推斷,楊氏模量Ep、電阻率φp、密度ρp對荷電過程影響最大。當楊氏模量增大時,材料形變減小,接觸時間縮短,顆粒電荷降低;當電阻率增大時,電荷交換受到抑制,顆粒電荷降低;當密度增大時,顆粒由于重力作用與壁面的碰撞更劇烈,顆粒電荷增大。PTFE、固氧、PMMA的楊氏模量和電阻率依次增大,密度依次減小,能夠對上述分析進行驗證。表3中的模擬結果顯示,顆粒電荷隨楊氏模量、電阻率的增加和密度的降低逐漸減少,與上述分析完全相符。

表3 顆粒物性對電荷積聚的影響

3 結 論

本文針對含固氧顆粒的液氫管路中靜電積聚規律及影響因素開展了仿真預示,所得結論如下。

(1)在固氧顆粒-壁面的碰撞與分離過程中,電荷傳遞的微觀過程是電子在接觸電勢差驅動下進行轉移。在液氫流速為10 m·s-1的工況下,液氫管流中稀相固氧α-O2顆粒的積聚比電荷Qsc約為10 μC·kg-1,顆粒電荷Qav約為10 pC,出口電流Iout約為0.5 μA。同時,兩相流的電荷密度為2.84×10-4C·m-3,較純液氫流大8個量級。

(2)固液兩相流動中,電荷積累效應包括顆粒電荷隨時間和位移的變化規律。管道出口處的顆粒總電荷Qout隨顆粒群的流動逐漸增加并趨于穩定。另外,壁面區域的顆粒電荷遠高于流動核心區,并通過顆粒間碰撞向核心區傳遞電荷。顆粒電荷隨流動距離增加逐漸飽和,在固氧顆粒粒徑為1 000 μm的工況下,顆粒積聚飽和電量約為84 pC。

(3)當顆粒質量流量一定時,比電荷Qsc隨著粒徑的增加存在極小、大值,分別為11.29、12.12 μC·kg-1;當粒徑一定時,比電荷Qsc隨著顆粒質量流量的增加略有降低;當顆粒物性一定時,比電荷Qsc隨管長增加和管徑降低逐漸增大,且隨流速的增加存在極小值,為11.41 μC·kg-1;顆粒物性對電荷積聚的影響主要體現在顆粒楊氏模量、電阻率和密度上。