融合多策略的改進黏菌算法及工程應用

李夢真,莫愿斌

(廣西民族大學 人工智能學院,廣西 南寧 530006)

0 引 言

近年來,隨著科學技術的不斷發展,計算復雜性的增強,優化問題在現階段受到廣泛關注,利用元啟發式算法求解多種復雜優化問題也是當下研究的熱點。常見的元啟發式算法有粒子群算法(Particle Swarm Optimization,PSO)[1]、布谷鳥算法(Cuckoo Search,CS)[2]、差分進化算法(Differential Evolution,DE)[3]、灰狼優化算法(Grey Wolf Optimizer,GWO)[4]、鯨魚優化算法(Whale Optimization Algorithm,WOA)[5]、海鷗優化算法(Seagull Optimization Algorithm,SOA)[6]、麻雀優化算法(Sparrow Search Algorithm,SSA)[7]、阿基米德優化算法(Archimedes Optimization Algorithm,AOA)[8]、斑點鬣狗優化算法(Spotted Hyena Optimization,SHO)[9]等等。

黏菌算法是2020年Li等人[10]根據黏菌個體振蕩捕食行為提出的,建立了由黏菌行為模式啟發的數學模型,實驗證明該算法具有良好的尋優能力,并廣泛應用于解決優化問題;文獻[11]提出了一種基于成敗歷史存檔的融合龍格庫塔黏菌算法,改進后算法的求解精度和魯棒性更具競爭力;文獻[12]利用精英反向學習和二次插值提升算法全局尋優性能、收斂精度及局部開發能力,幫助算法跳出局部極值;文獻[13]提出了一種融合精英策略的SMA,在有固定頻率約束的桁架結構尺寸優化問題中取得較好結果。該文提出的融合多策略的改進黏菌算法包含三個改進策略,能針對原算法存在的缺點進行整合性提升。首先,采用Sine映射初始化種群,提高種群多樣性;其次,引入自適應變異t分布策略,改進原算法容易陷入局部最優的缺點;最后,引入黃金正弦機制來改進算法在迭代后期收斂速度慢、收斂精度低的問題。通過基準測試函數及CEC2021測試函數對改進后的黏菌算法進行性能測試,測試結果明顯優于其他對比算法,然后將其應用于工程應用問題,GTSMA都取得了理想的結果。

1 黏菌算法

黏菌算法生物背景新穎,結構清晰,主要利用黏菌覓食的潛力與特性來解決復雜的優化問題。黏菌覓食的潛力最初體現在路徑規劃中,該算法主要模擬黏菌靠近食物、包圍食物和獲得食物三個階段。首先,黏菌根據空氣中的氣味濃度去接近食物,黏菌個體會根據公式1的規則進行更新移動:

(1)

其中,X表示黏菌的當前位置,LB與UB表示搜索范圍的上下邊界,XA與XB表示從所有黏菌個體中隨機挑選的兩個個體,Vb是介于[-a,a]的參數,迭代次數越多,Vb的值越趨于0,Vc從1-0呈線性變化,t表示黏菌個體當前的迭代次數,權重參數W表示黏菌的質量,Xb(t)表示第t次迭代適應度最優的個體位置,r表示[0,1]區間的隨機值,其中控制變量p和參數a的函數表達式如式2、式3:

p=tanh|S(i)-DF|

(2)

(3)

其中,S(i)代表黏菌個體X的適應度,而DF表示最佳適應度值,tmax代表個體更新的最大迭代次數。而W的表達式如式4:

W(smellIndex)=

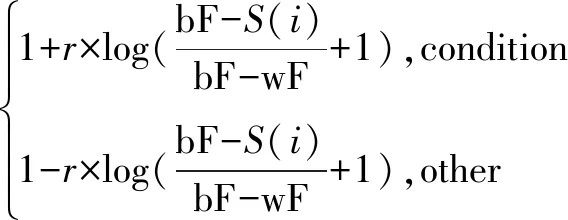
(4)

其中,condition表示適應度排在前一半的個體,other表示余下的種群個體,r表示[0,1]區間內的隨機值,bF和wF分別表示當前種群中的最好和最差適應度值。

2 融合多策略的改進黏菌算法

2.1 Sine混沌映射

豐富的初始種群,對于算法的收斂速度和尋優精度都十分重要。黏菌在初期的位置具有隨機性和不確定性,可能會出現種群分布不均勻,容易陷入局部最優。而混沌序列可以用來解決上述問題[14]。常見的混沌映射有logistic映射、kent映射等,該文采用Sine混沌映射,選取式5產生的初始變量值利用式6映射到黏菌個體上,產生多樣性較好的初始種群。

Yi+1=ρsin(πi)

(5)

(6)

其中,Yi∈[-1,1]為混沌序列;i=1,2,…,N表示種群規模;ρ為控制參數;Ud和Ld分別為黏菌個體在第d維的上限和下限。

2.2 自適應t分布變異策略

t分布最早被命名為“Student’s distribution”,高斯分布(Gaussian Distribution,GD)和柯西分布(Cauchy Distribution,CD)是t分布的兩個特殊邊界分布,該策略融合了高斯分布和柯西分布的優點,初期參數t取較小值,符合柯西分布;迭代進行到中后期時,t取值就會變大,t分布無限接近高斯分布。具體的黏菌位置更新方式如式7:

X(t+1)=

(7)

其中,ts是以SMA迭代次數為自由度的t分布,隨著S增加,t也會增加,t分布由開始的柯西分布逐漸轉變為高斯分布。

2.3 黃金正弦策略

黃金正弦算法(golden Sine Algorithm,goldenSA)[15]是引用黃金分割系數加入正弦函數設計來提升尋優性能的一種新型智能算法。算法開始時通過隨機生成N個個體來更新初始空間,在個體位置更新過程中,利用黃金分割系數來縮小個體的搜索空間。其位置更新公式如下:

(8)

3 GTSMA優化算法

3.1 算法流程

針對基本SMA的缺點,該文提出融合多策略的改進黏菌算法(GTSMA)。首先,引入Sine混沌映射提高迭代初期種群的多樣性;其次,隨著迭代次數的增加,自適應t分布變異策略中自由度參數t取值也會隨之變大,可以增加算法跳出局部最優的概率;最后與黃金正弦算法相結合。在算法迭代后期利用黃金分割系數對整個過程進行優化,改進算法在迭代后期收斂精度較低的問題。GTSMA流程如圖1所示。

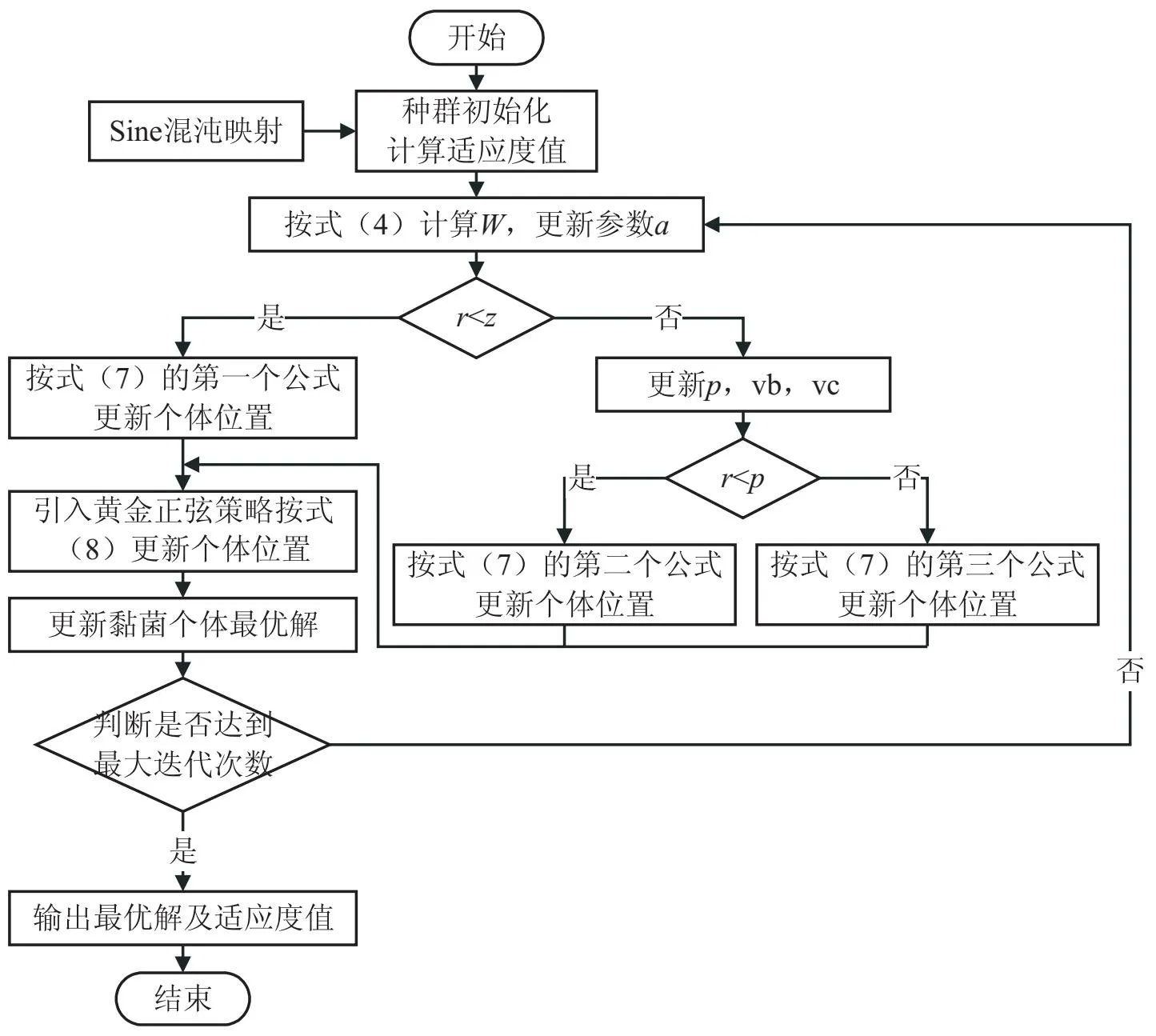
圖1 算法流程

3.2 算法的時間復雜度分析

設黏菌種群規模為N,問題維度為D,最大迭代次數為T,目標函數復雜度為Oobj。則GTSMA在Sine混沌映射初始化種群階段的時間復雜度為O(N×M),適應度值評估和排序的復雜度為O(T×N×(1+logN)),權重參數W更新時間復雜度為O(T),迭代后期融合黃金正弦更新最優位置的時間復雜度為O(T×M),最后階段位置更新的時間復雜度為O(T×N×M)。綜上所述,GTSMA的時間復雜度為O(T×N×(M+Oobj+1+logN))。

4 實驗仿真與結果分析

4.1 實驗環境

所有實驗代碼均在Matlab R2018a上運行,以保證公平的比較。

4.2 基準測試函數

選取單峰、多峰函數等不同類型的基準測試函數對GTSMA進行測試來驗證GTSMA的性能,函數的維數、范圍和理論最優值如表1所示。

表1 基準測試函數

4.3 GTSMA與其他算法對比

論文通過對WOA,PSO,GWO,CS,SMA,GTSMA分別在6個測試函數獨立運行30次的結果進行對比來檢驗文中改進策略是否有效,運行結果見表2。

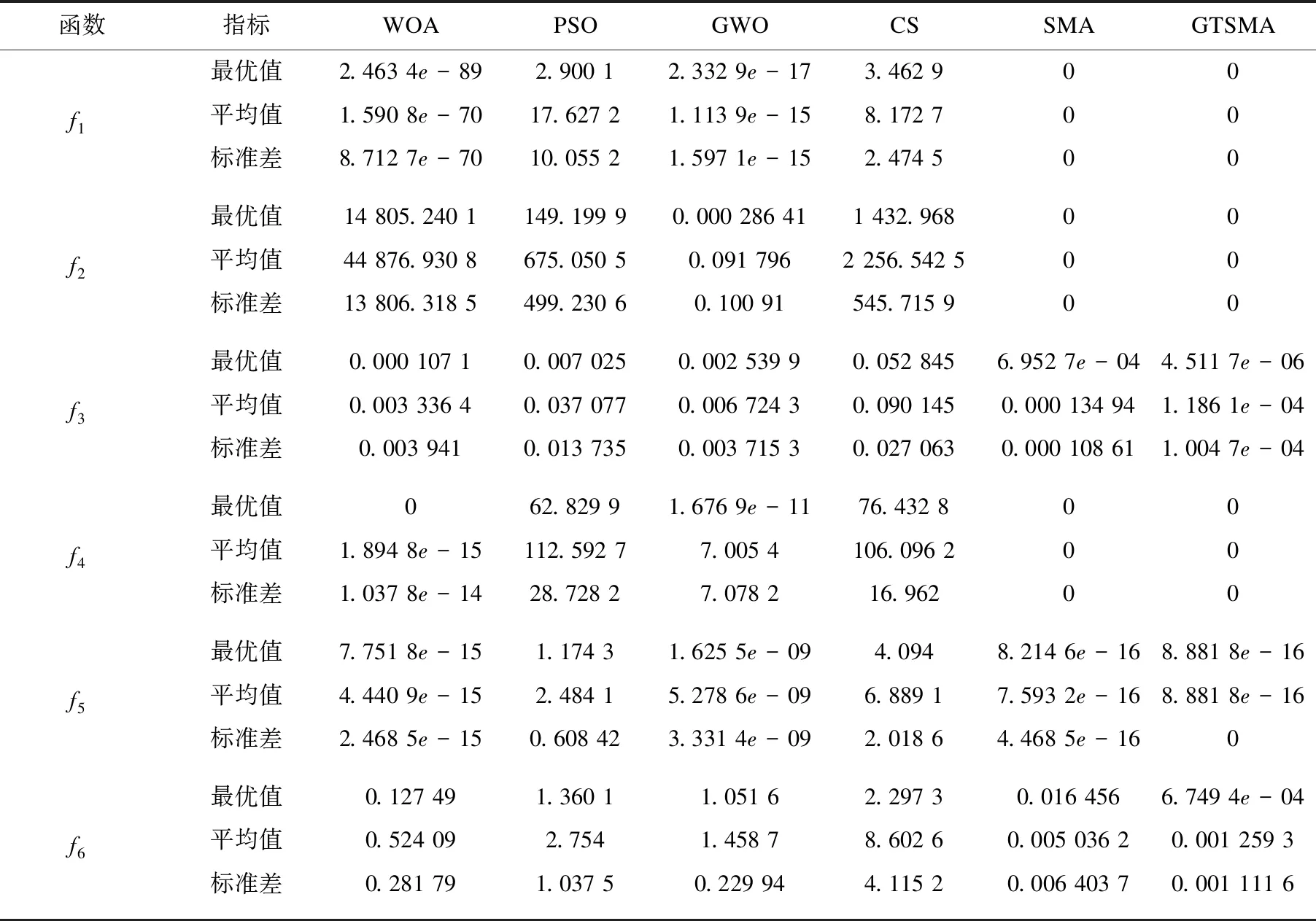
表2 所有比較算法的運行結果

由表2數據可知,針對不同類型的函數,GTSMA的綜合性能最強。對于函數f3,f5,f6,GTSMA的三項指標均優于原始SMA。由圖2可以更直觀看出GTSMA效果更理想。對于函數f1,f2, 其他比較算法收斂精度較低,GTSMA相對于原始SMA收斂到最優值所需迭代次數更少。對于函數f4,算法迭代初期該函數的收斂曲線下降明顯、收斂速度快。對于函數f5,GTSMA只需五十多次迭代即可獲得理論上最優值。對于f3,f6,從圖中可以看出函數拐點次數明顯增多,說明該算法不僅能夠快速收斂,而且還能在后期的迭代過程中快速逃離局部最優,提高了算法的勘探能力。

(a)f1比較算法收斂曲線 (b)f2比較算法收斂曲線 (c)f3比較算法收斂曲線

4.4 CEC2021測試集實驗分析

在CEC2021測試集上與其他同類型算法進行對比,檢驗GTSMA的綜合性能,CEC2021測試函數見表3。

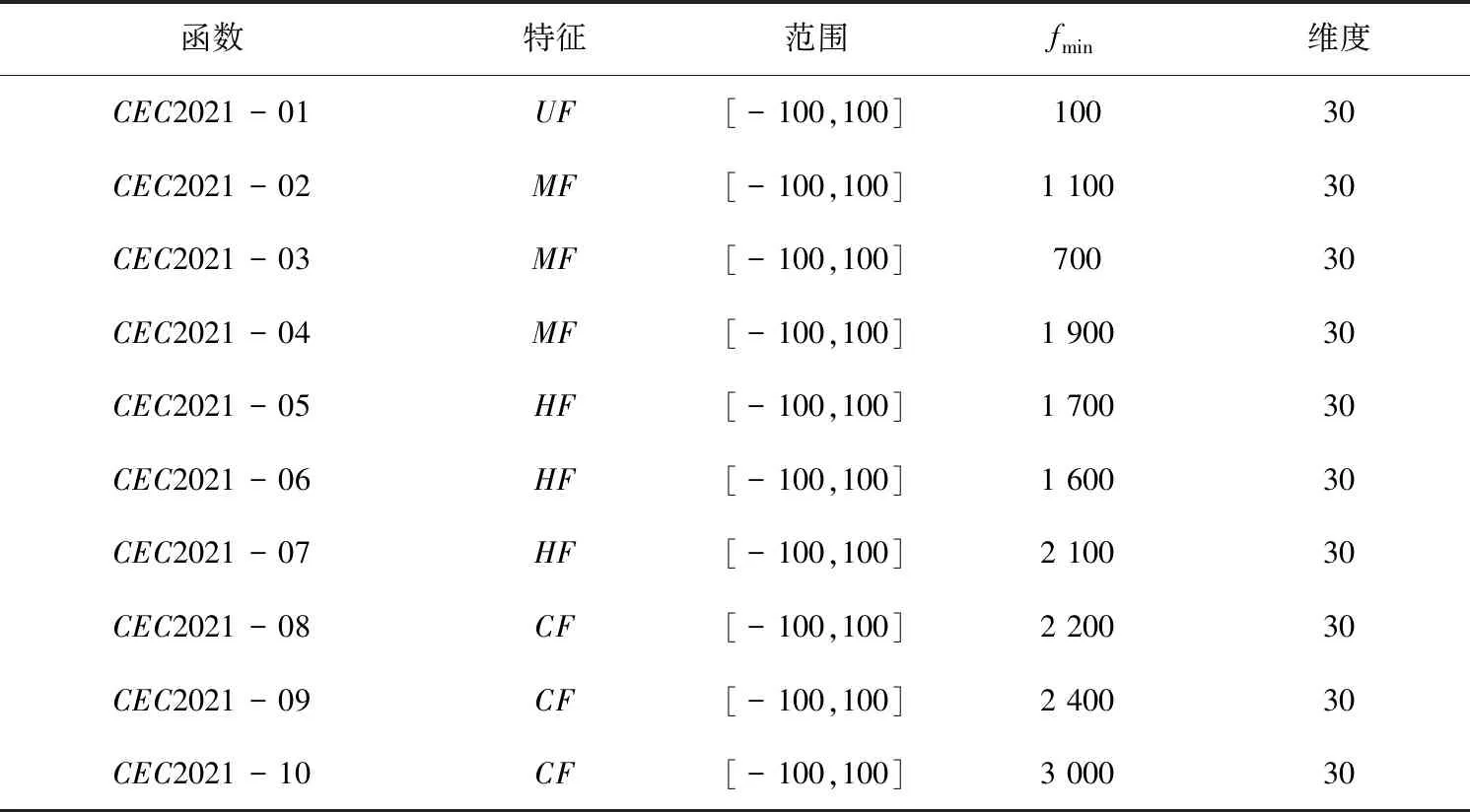
表3 CEC2021測試集

將GTSMA與標準SMA,SOA,WOA,DE以及GWO進行對比。實驗參數取種群規模為N=30,維度d=30,最大迭代次數為500。表4展示了算法在運行過程中取得的最優平均值和標準差。由表4中算法的運行結果可知,GTSMA在10個測試函數中平均值和標準偏差均為0,根據上述實驗結果分析,GTSMA相比同類算法優勢更大。

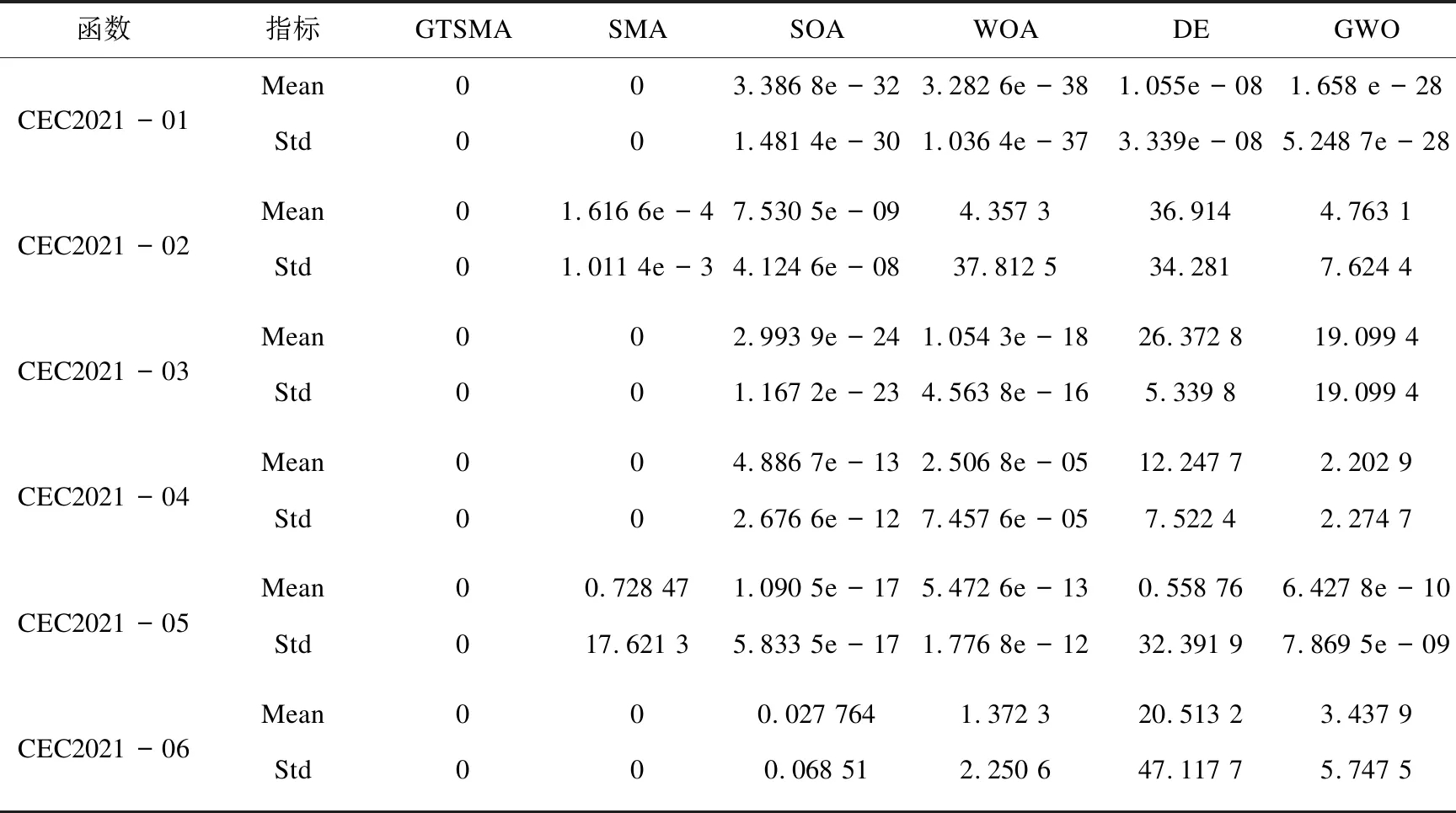
表4 所有比較算法CEC2021測試集實驗結果

5 GTSMA在工程優化問題的應用

拉壓彈簧設計問題作為優化工程應用問題中的經典案例,結構模型如圖3所示,它的目標是在滿足一定約束條件下令彈簧質量f(x)最小。該問題主要包括彈簧金屬絲直徑D(x1)、彈簧圈平均直徑D(x2)以及彈簧的有效圈數N(x3)三個設計變量以及最小撓度、剪切應力、振蕩頻率以及外徑限制四個不等式約束。其數學模型如式9所示。

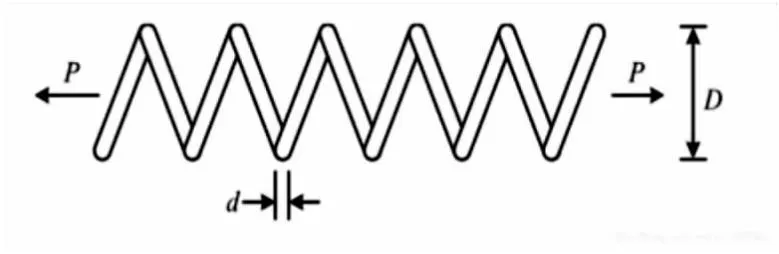
圖3 壓力彈簧模型

約束條件為:

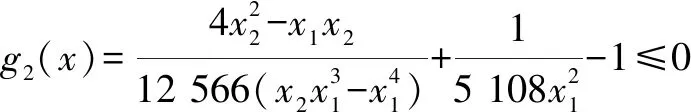
(9)

其中,變量x1,x2,x3的取值范圍如下:

0.05≤x1≤2,0.25≤x2≤1.3,2≤x3≤15

用GTSMA和標準SMA求解拉壓彈簧設計問題,并與WOA[5],SSA[7],AOA[8],混沌粒子群算法(Chaos particle swarm optimization algorithm,CPSO)[16]取得的最優值進行對比。為確保數據的準確性,用于比較算法的數據均取自于對應的參考文獻。其中對比結果如表5所示。

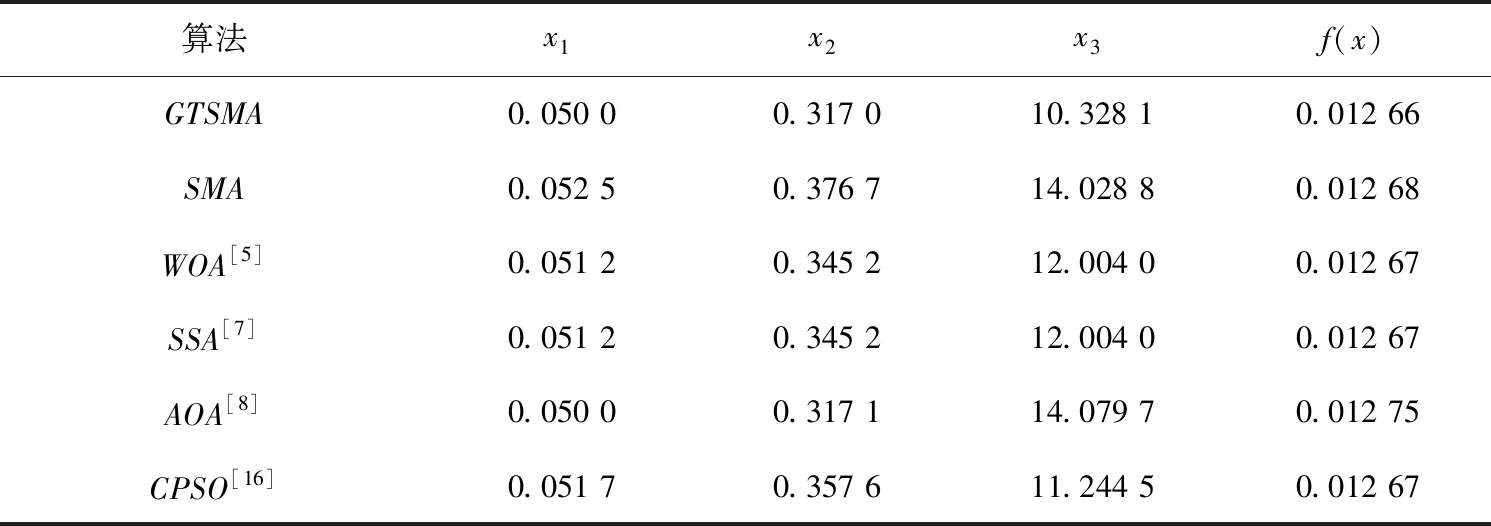
表5 拉壓彈簧設計問題優化結果

從表5的數據可知,在拉壓彈簧設計問題尋優結果中,GTSMA的尋優結果為0.012 66,結果均優于其他四種優化算法。因此,GTSMA的尋優能力更強,可以有效地處理拉壓彈簧工程問題。

6 結束語

在原始SMA的基礎上,提出了一種融合多策略的改進黏菌算法,迭代初期在種群初始化過程中引入Sine混沌序列提高種群多樣性;然后引入自適應t分布策略避免黏菌個體陷入局部最優;最后融合黃金正弦算法思想更新個體位置,提高算法的收斂精度及運行速度。在基準測試函數、CEC2021測試集以及實際工程設計優化問題上均取得了滿意效果,表明了GTSMA的可操作性和適用性。今后的工作將繼續研究改進的優化策略,提高該算法的運行速度并將其應用到更復雜的優化問題中。