禁用兩個子圖的圖的全控制數

楊樹承, 胡夫濤, 張昶旭

(安徽大學 數學科學學院,合肥 230601)

1 研究背景

本文中的圖G=(V(G),E(G))是頂點集為V(G),邊集為E(G)的無環且無重邊的簡單無向圖,圖G的任一頂點v,其開鄰域N(v)為在G中和點v相鄰的所有點的集合,閉鄰域記為N[u]=N(u)∪{u}.頂點v的度是指與v相鄰點的數目,記為d(v)=|N(v)|.如果頂點v的度為0,則稱它為孤立點.圖G中點的度的最小值和最大值為圖G的最小度和最大度, 分別用δ(G)和Δ(G)表示.如果圖的頂點數目|V(G)|=n, 則稱圖G為n階圖.通常用e=uv表示G中的一條邊,其中u和v是e的兩個端點, 稱u和v是鄰接的, 記為u～v.如果圖G的任意兩個點都有路相連,則稱圖G為連 通圖.設S?V,稱頂點集為S, 邊集為G中兩個端點都在S中的圖為由S生成的導出子圖,記為〈U〉.沒有給出定義的基本符號和圖論術語[1].把n個頂點順次連接起來形成的圖稱為路, 記為Pn.含有n個點的完全圖, 記為Kn, 是指任意兩個頂點都鄰接的簡單圖.如果一個圖G的頂點集可以被劃分成兩個子集X,Y, 并且每條邊一端點在X中另一個端點在Y中, 那么G稱為二部圖, 記作G[X,Y].如果圖G[X,Y]在集合X中的每一個頂點都和Y中的每一個頂點鄰接,則稱G為完全二部圖, 設|X|=s,|Y|=t, 完全二部圖G表示為Ks,t.特別的K1,3稱為爪圖, 見圖1.

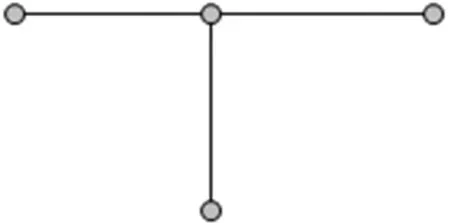
圖1 爪圖K1,3.Figure1 Claw graph K1,3

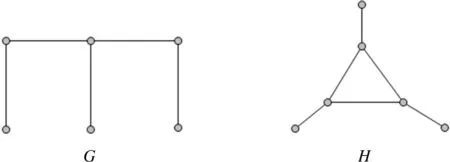
圖2 圖G是E圖,圖H是網圖Figure 2 Graph G was E graph,graph H was net graph

圖3 D圖Figure 3 D graph

設D是V的子集.若不在D中的每個點都至少和D中一點相鄰, 則稱D為G的控制集.最小控制集所含的頂點數稱為圖G的控制數,記為γ(G).根據實際需要, 還引申出很多其他變形的控制.如果不含孤立點的圖G的控制集D的導出子圖〈D〉不含孤立點, 則稱D為G的全控制集.圖G的最小全控制集含有的頂點數稱為全控制數, 記為γt(G).Pfaff等[2]證明了求解圖的全控制數是NP-完備的.

圖的控制數的研究可以追溯到1850年.圖的控制問題和相關子集問題的研究是圖論研究中心熱點,引起了人們廣泛的研究, 相關研究成果有幾千篇論文[3-6].在圖的控制論中,圖的全控制是研究比較多的.Henning于2009年撰寫了一篇圖的全控制問題的綜述[7].

對于無爪圖的全控制數的研究有很多[8-9].對于禁用兩個子圖的圖的全控制數研究暫時還未見到.本文考慮了禁用爪圖和D圖的N≥2階連通圖G全控制數得到γt(G)≤2「n/4?.

2 主要結論

設G=(V,E)是一個簡單無向圖,u是V中任一點和X是不包含u的頂點子集.記d(u,X)是G[X∪{u}]中最長的以u為端點的路的長度.設S?V,記

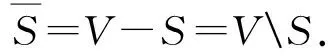
引理2.1 如果P=v1v2…vl是G中的一條最長路,則對任意i∈[l-1],

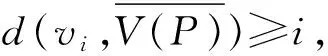
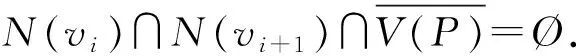
對于禁用兩個子圖的圖的成對控制數研究暫時還未見到.本文得到了無爪圖和無D圖時全控制數的上界.

定理2.1 設G是n≥2階連通無爪和無D的圖,則γt(G)≤2「n/4?.

證明：首先考慮n≤6的情形.設u是G中的一個最大度點.當Δ(G)≤n-2時,G至多有一個點v不與u相鄰,此時這樣的點v一定與u的某個鄰點w相鄰,則{u,w}是G的一個全控制集,所以γt(Pn)≤2.當Δ(G)=2時,G是階數為n的路Pn,此時γt(Pn)≤2「n/4?.剩余的情況為n=6且d(u)=3.設G不與u相鄰的兩個點為s,t.若s～t,則{u,w,s,t}是G的一個全控制集,所以γt(G)≤4.若點s與點t不相鄰,則{u,s′,t′,t}是G的一個全控制集,其中s′∈N(s)∩N(u),t′∈N(t)∩N(u),所以γt(G)≤4.

下面設n>6.下證總是存在U?V(G),|U|=m且4≤m≤6,〈U〉是連通的,使得γt(〈U〉)≤「m/2?且〈V-U〉是連通的.此時根據歸納法原理γt(G)≤γt(〈U〉)+γt(〈V-U〉)≤2「m/4?+2「n-m/4?≤2「n/4?.

N(v1)?S,

N(v2)?S.

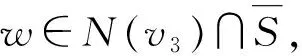
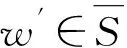
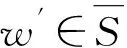
情形1v1～v3.N(w)∩{v1,v2,…,v6}=?且N(v1)∩{v4,v5,v6}=?.

取U={v1,v2,v3,v4,w},〈U〉是連通的,γt(〈U〉)=2且〈V-U〉是連通圖.

情形2v1～v7.N(w)∩{v1,v2,…,v6}=?且N(v1)∩{v3,v4,v5,v6}=?.

取U={v2,v3,v4,w},〈U〉是連通的,γt(〈U〉)=2且〈V-U〉是連通圖.

情形3v2～v4.N(w)∩{v1,v2,…,v6}=?且N(v1)∩{v3,v4,v5,v6,v7}=?.

取U={v1,v2,v4,w},〈U〉是連通的,γt(〈U〉)=2且〈V-U〉是連通圖.

情形4v2～v5.N(w)∩{v1,v2,…,v6}=?,N(v1)∩{v3,v4,v5,v6,v7}=?,N(v2)∩{v4}=?.

由于〈v2,v4,v5,v6〉不是爪圖,一定有v2～v6或v4～v6.分以下2種情形考慮.

1)v2～v6

2)v4～v6

情形5v2～v6.N(w)∩{v1,v2,…,v6}=?,N(v1)∩{v3,v4,v5,v6,v7}=?,N(v2)∩{v4,v5}=?.

情形6v2～v7.N(w)∩{v1,v2,…,v6}=?,N(v1)∩{v3,v4,v5,v6,v7}=?,N(v2)∩{v4,v5,v6}=?.

情形7v3～v6.N(w)∩{v1,v2,…,v6}=?,N(v1)∩{v3,v4,v5,v6,v7}=?,N(v2)∩{v4,v5,v6,v7}=?.

情形8v3～v7.N(w)∩{v1,v2,…,v6}=?,N(v1)∩{v3,v4,v5,v6,v7}=?,N(v2)∩{v4,v5,v6,v7}=?,N(v3)∩{v6}=?.

情形9v4～v6.N(w)∩{v1,v2,…,v6}=?,N(v1)∩{v3,v4,v5,v6,v7}=?,N(v2)∩{v4,v5,v6,v7}=?,N(v3)∩{v6,v7}=?.

情形10v4～v7.N(w)∩{v1,v2,…,v6}=?,N(v1)∩{v3,v4,v5,v6,v7}=?,N(v2)∩{v4,v5,v6,v7}=?,N(v3)∩{v6,v7}=?,N(v4)∩{v6}=?.

由于〈w,v3,v4,v7〉不是爪圖,所以v3～v7.由于v3～v7已經在情形8中進行了詳細的討論,這里不再贅述.

情形11v5～v7.N(w)∩{v1,v2,…,v6}=?,N(v1)∩{v3,v4,v5,v6,v7}=?,N(v2)∩{v4,v5,v6,v7}=?,N(v3)∩{v6,v7}=?,N(v4)∩{v6,v7}=?.

3 結 語

注意到,對于至少含兩個點的路Pn,γt(Pn)≤2「n/4?.顯然路是不含爪和D的圖,因此定理2.1給出的上界是緊的.

對于n階無爪連通圖G的全控制數的研究非常多,2000年,Favaron和Henning[10]證明了:若δ(G)≥3, 則γt(G)≤n/2.2007年, Stephan和Anders[11]證明了:δ(G)≥4,則γt(G)≤3n/7.對于有兩個禁用子圖的全控制數研究還比較少,本文給出了無爪圖和不含D圖的全控制數的上界.此后可以考慮禁用其他兩個子圖的全控制數的上界問題,比如禁用一些比D圖更大一點的子圖.