公交車移動荷載作用下淺埋電力隧道結構動力響應分析

田 崗，金春峰，侯代敏，張海軍，郭起林，段艷芳

（1.中國電子工程設計院有限公司，北京 100142；2.中電投工程研究檢測評定中心有限公司，北京 100142）

0 引言

近年來，隨著我國社會經濟的不斷進步，城市基礎設施得到快速發(fā)展，電力隧道作為一種城市中較為常見的電力基礎設施，其埋深相對較淺，廣泛分布于城市的

各個區(qū)域，并與城市道路網相互交叉或并行，不可避免地會受到城市交通荷載的影響。城市交通荷載是一種可變動的荷載，其作用效應與車輛軸重密切相關，不斷激勵著道路地下土體和電力隧道，極易引起周邊土體和電力隧道出現(xiàn)振動破壞效應，導致土體結構弱化，甚至誘發(fā)電力隧道工程災變現(xiàn)象，因此，開展城市交通荷載對電力隧道動力響應研究，具有十分重要的工程現(xiàn)實意義。

目前，針對外部荷載作用對隧道及周邊環(huán)境的影響效應研究，國內外學者開展了多方面的探索與討論。如皮映星［1］利用 ADINA8.5 有限元軟件建立了二維隧道分析模型，分析了圍巖和襯砌受交通荷載影響下的位移、應變的變化規(guī)律；羅紅星等［2］發(fā)現(xiàn)在隧道開挖施工且無初支的情況下，公路車輛荷載對隧道整體變形影響較大，路面也易產生裂縫；魏綱等［3］利用 Midas GTS 軟件對沉管隧道路床網格節(jié)點添加線性變化的荷載，來模擬分析車輛行駛對管節(jié)及接頭產生的動力響應；白旭峰等［4］通過建立管廊隧道的三維有限元分析模型，并將車輛荷載簡化為靜力荷載，分析車輛荷載作用下軟土地基上綜合管廊的受力變形特征；趙健等［5］運用 ANSYS 軟件建立道路三維動力分析模型，分析了不同車輛荷載工況下道路的動力響應；Omar Chaallal 等［6］通過三維有限元模型，模擬汽車荷載作用下對路面以下埋管的影響；徐健等［7］通過建立綜合管廊-路基土-車輛荷載有限元模型，探討了行車速度、車輛荷載加載位置對綜合管廊頂板位移的影響規(guī)律；李磊［8］利用 ABAQUS 有限元軟件對車輛荷載、管廊結構-土體和樁的相互作用、綜合管廊的動靜響應進行研究。

總之，上述研究主要集中在交通荷載對隧道結構受力特性和變形特征的影響方面，且大多將交通荷載進行了靜力簡化，亦或是建立了動力分析模型，但考慮的或是車輛在隧道內部運行時的結構響應特征，或是車輛運行對道路的影響等。鮮有學者對車輛-道路-電力隧道這種組合形式進行深入分析，研究其內在的結構動力響應特征。基于此，本文以某既有電力隧道為例，利用Midas NX 有限元軟件，建立考慮公交車荷載-道路-電力隧道多元耦合的動力分析模型，重點分析電力隧道及周邊土體受公交車荷載作用下的動力響應特征和振動規(guī)律，以期為后續(xù)電力隧道運營安全提供技術參考。

1 工程概況

1.1 工程背景

某城市既有電力隧道始建于 20 世紀 70 年代，現(xiàn)狀良好，埋深約 0.5 m，其結構形式為矩形磚混隧道（頂、底板為預制混凝土結構，左、右邊墻為砌體磚墻結構），建筑尺寸寬×高為 2.2 m×2.2 m，隧道頂、底板厚 0.2 m，混凝土強度等級為 C25，鋼筋強度等級為Q235；左、右邊墻厚 0.37 m，磚強度等級為 MU10，砂漿強度等級為 M5。電力隧道正交下穿城市主干道路，該主干道路路面面層為瀝青路面，厚約 0.2 m，基層為石灰粉煤灰穩(wěn)定碎石土，厚約 0.5 m，該段道路車流密集，交通流量較大。

1.2 地質條件

根據(jù)隧址段區(qū)域勘察資料顯示，本場區(qū)除表層為人工填土（Qs）外，其余主要由第四系全新統(tǒng)（Q4al-pl）和上更新統(tǒng)（Q3al-pl）沖洪積地層組成，具體如下。

1）人工填土層（Qs）。

場區(qū)表層主要以堆積粉土、黏性土填土及雜填土為主，局部為種植土，該層揭露層厚一般 2.5～4.5 m。

2）第四系全新統(tǒng)沖洪積地層（Q4alp）。

粉質黏土②層:該層土質不均，以粉質黏土、粉土互層形式分布，局部有機質含量較高，夾少量粉砂層透鏡體，該層層厚一般 6～8 m。

中細砂③層:以細砂為主，褐黃色，濕，偶見礫，密實，局部中密，揭露層厚一般 2～4 m，局部約 5 m。

卵石④層:局部為圓礫，雜色，濕～飽和，多為密實，上部局部呈中密狀，一般粒徑 2～5 cm，勘探揭露最大粒徑約 16 cm，亞圓形，中砂充填，偶含漂石，級配良好，卵石含量多為 58 %～69 %，局部夾薄層中細砂透鏡體及黏性土薄層，該層層厚 10～15 m。

3）第四系上更新統(tǒng)沖洪積地層（Q3alp）。

黏土⑤層與中細砂⑤1層互層:土質不均，該層層厚一般 2～3 m，局部約 4 m。

卵石⑥層:雜色，飽和，密實，一般粒徑 4～6 cm，鉆探揭露最大粒徑＞10 cm，亞圓形，局部含漂石，級配良好，中砂充填為主，卵石含量為 44 %～63 %。局部含密實狀砂層透鏡體，該層層厚 7～10 m。

2 數(shù)值模擬

2.1 模型建立

結合電力隧道結構特征和區(qū)域地層情況，建立考慮“公交車荷載-道路-電力隧道”多元耦合的動力分析模型，模型長×寬×高為 16 m×16 m×8 m，自上而下分別為道路面層、基層、填土層、粉質黏土層，均為三維實體單元，面層厚為 0.2 m，基層厚為 0.5 m，填土層為 2.8 m，粉質黏土層厚為 4.5 m。此外，電力隧道位于模型中部，距離面層以下 0.5 m 處，頂、底板為三維實體單元，厚度為 0.2 m，左、右邊墻為二維板單元，厚度為 0.37 m。其中，頂板設置有直徑為 0.014 m 的鋼筋，間距為 0.1 m，距離頂板底面 0.02 m，鋼筋為一維梁單元。底層模型與隧道及頂板鋼筋模型如圖1 所示。

圖1 三維分析模型

2.2 參數(shù)設置

根據(jù)隧址區(qū)域現(xiàn)場地質狀況、電力隧道及道路設計資料，對模型材料參數(shù)進行賦值。其中，面層、基層、頂?shù)装濉⒆笥疫厜弯摻畈捎脧椥员緲嫞钔翆雍头圪|黏土層采用摩爾庫倫本構。具體模型參數(shù)設置如表1 所示。

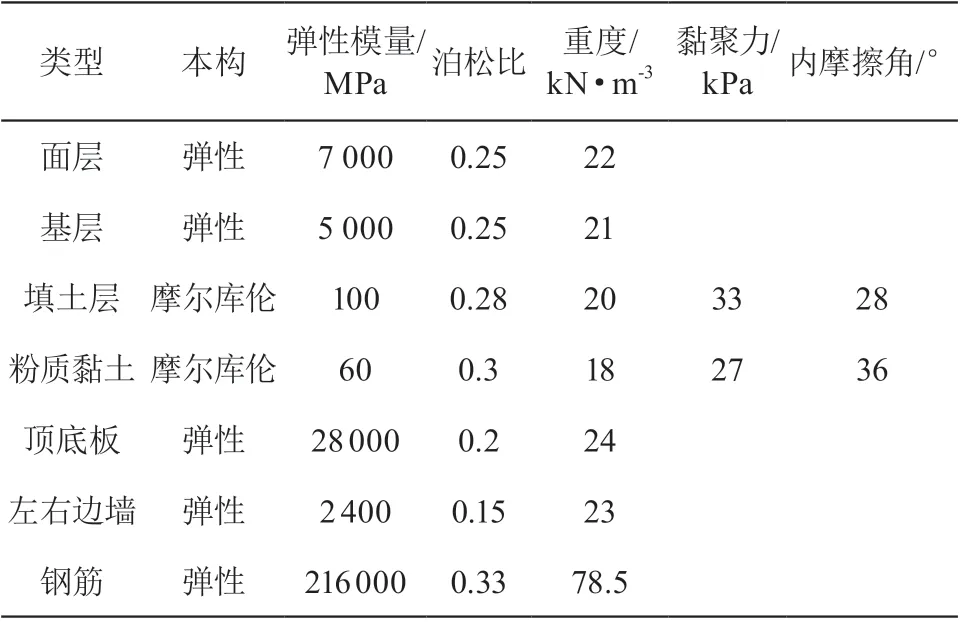
表1 模型材料參數(shù)

2.3 邊界條件

本文中模型主要受公交車移動荷載作用的影響，當模型受到外荷載激勵時，將會產生一定的振動響應，為了吸收振動反射波在模型邊界的影響，本文將該模型邊界設置為粘彈性邊界。即在 Midas NX 軟件中對模型前、后、左、右四個側面以及底面設置地面曲面彈簧，以實現(xiàn)粘彈性邊界的施加，如圖2、3 所示。

圖2 粘彈性邊界

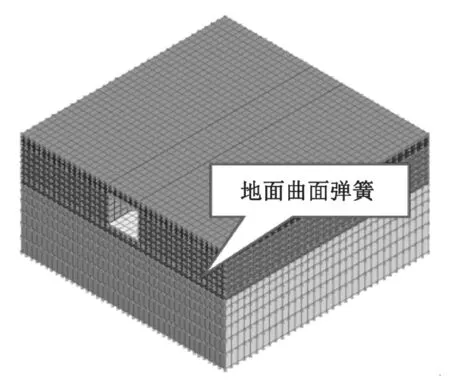
圖3 地面曲面彈簧

2.4 荷載施加

本文中模型主要考慮了自重荷載和公交車荷載的作用，其中，自重荷載作用可直接在模型中施加為豎直向下的重力；公交車荷載作用則考慮到路面的不平順性，導致車輛行駛過程中會產生一定頻率的振動，公交車荷載隨時間變化值可表示為車輛恒載+附加動載的形式［9］，如式（1）、（2）所示。

式中:Ph為車輛恒載，kN；Pd（t）為車輛附加動載，kN；Pdmax為車輛附加動載最大幅值，kN；T為車輛附加動載作用周期，s；t為時間，s。

此外，工程上一般常將Pdmax取 0.2Ph［10］，同時本文考慮到電力隧道跨度較小，為了保證得到最大車輛荷載狀況下對電力隧道的影響，本文將式（1）進行簡化，即只考慮最大車輛荷載作用的影響，如式（3）所示。

由于城市公交車多為兩軸車輛，其空載重量為120 kN，滿載重量為 180 kN，本文取半載重量 150 kN 進行計算，同時考慮 1.2 的放大系數(shù)，則模型需施加的車輛荷載為 180 kN，即單軸軸重為 90 kN。同時，對其施加 36、54、72 km/h 三種車速，分析不同車速情況下公交車移動荷載對電力隧道及周邊道路的影響（如圖4、5 所示）。

圖4 模型車輛荷載設置

圖5 荷載施加形式

3 結果分析

為了便于分析討論 36、54、72 km/h 三種不同車速下，公交車移動荷載作用對電力隧道及其周邊道路的影響，本文于模型中分別選取路面節(jié)點 29347#、隧道頂板節(jié)點 108334# 以及鋼筋單元 90316# 作為結果監(jiān)測位置（見圖6），分析公交車分別以 36、54、72 km/h 三種車速通過時，電力隧道及其周邊路面的振動響應情況。

圖6 振動效應監(jiān)測位置

3.1 沉降分析

如圖7～9 可以看出，在 36、54、72 km/h 三種車速的情況下，路面的最大沉降量分別為 0.176、0.175、0.182 mm，隧道頂板最大沉降量分別為 0.155、0.155、0.161 mm，路面最大沉降量高于隧道頂板最大沉降量。在 36km/h 和 54km/h 車速下，路面和隧道頂板的最大沉降量基本沒有變化，而當車速提高到 72km/h 時，路面和隧道頂板的最大沉降量均略有增長。

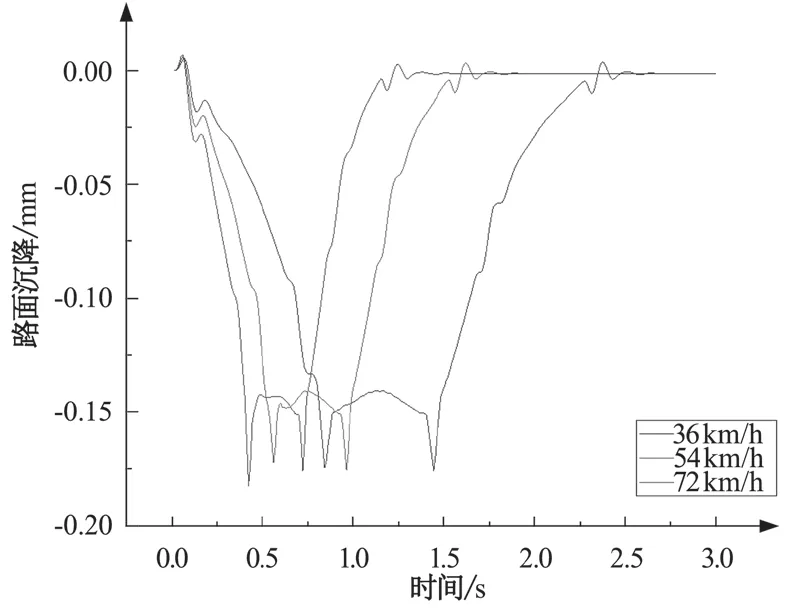
圖7 路面沉降時程曲線

圖8 隧道頂板沉降時程曲線

圖9 不同車速下的沉降量

3.2 振動速度分析

由圖10～12 可以看出，在 36、54、72 km/h 三種車速情況下，路面最大振動速度幅值分別為 1.673、2.565、3.080 mm/s，隧道頂板最大振動速度幅值分別為 0.773、1.129、1.270 mm/s，路面最大振動速度幅值高于隧道頂板最大振動速度幅值。整體上路面和隧道頂板的最大振動速度幅值均呈現(xiàn)出隨車速提高而增大的趨勢，但隨著車速提高，路面和隧道頂板的最大振動速度幅值增長量逐漸減小。

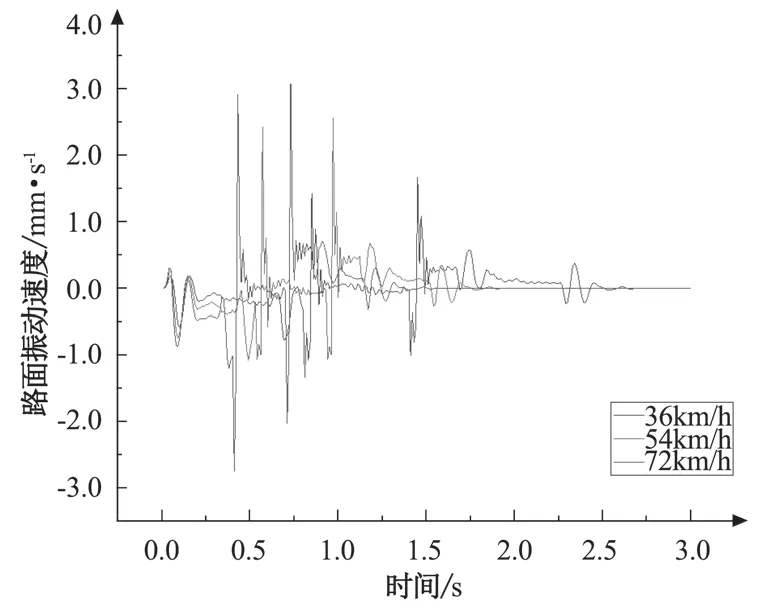
圖10 路面振速時程曲線

圖11 隧道頂板振速時程曲線

圖12 不同車速下的振動速度

3.3 振動加速度分析

由圖13～圖15 可以看出，在 36、54、72 km/h 三種車速情況下，路面最大振加動速度幅值分別為 441.513、1 024.843、631.159 mm/s2，隧道頂板最大振動加速度幅值分別為 59.595、99.890、152.619 mm/s2，路面最大振動加速度幅值高于隧道頂板最大振動加速度幅值。其中，路面最大振動加速度幅值隨著車速提高先增大后減小，而隧道頂板最大振動加速度幅值隨著車速提高逐漸增大。

圖13 路面振動加速度時程曲線

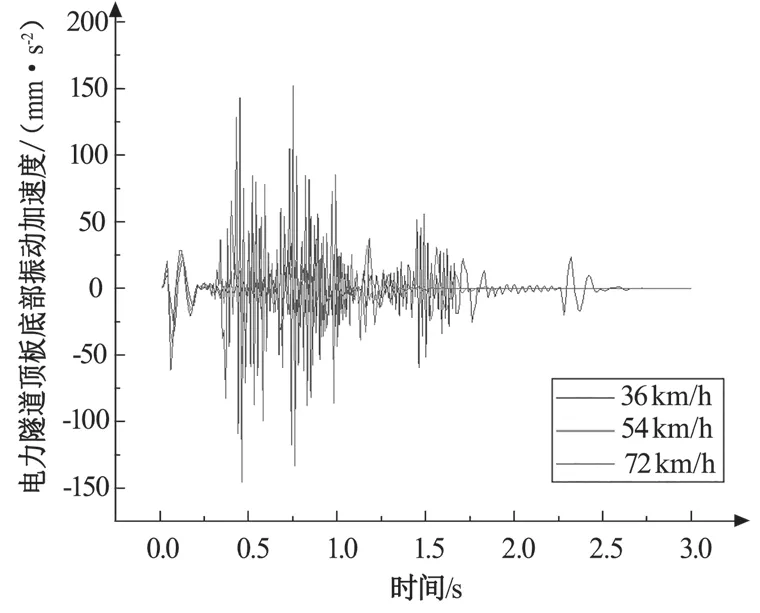
圖14 隧道頂板振動加速度時程曲線

圖15 不同車速下的振動加速度

3.4 振動應力分析

由圖16～18 可以看出，在 36、54、72 km/h 三種車速情況下，路面最大振動應力幅值分別為 370.253、359.444、365.752 kPa；隧道頂板最大振動應力幅值分別為792.446、792.725、793.629 kPa，路面最大振動應力幅值低于隧道頂板最大振動應力幅值。其中，路面最大振動應力幅值隨著車速提高先減小后增大，而隧道頂板最大振動加速度幅值隨著車速提高逐漸增大，但整體上車速對路面和隧道頂板的最大振動應力幅值的影響不大。此外，由于本文電力隧道混凝土強度等級為 C25，其抗拉強度標準值為 1 780 kPa，因此，在公交車 36、54、72km/h 三種車速情況下，隧道頂板底部最大拉應力幅值分別達到抗拉強度的 44.52 %、44.54 % 和 44.59 %，均滿足正常使用要求。

圖16 路面應力時程曲線

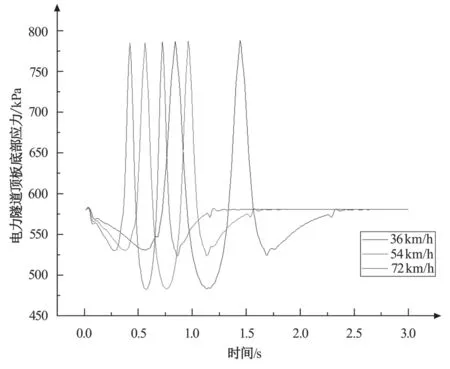
圖17 隧道頂板應力時程曲線

圖18 不同車速下的振動應力

3.5 鋼筋軸向應力分析

由圖19 和圖20 可以看出，在 36、54、72 km/h 三種車速情況下，隧道頂板鋼筋軸向振動應力幅值分別為4 592.778、4 591.907、4 598.286 kPa。車速對鋼筋軸向振動應力幅值的影響不是太明顯，整體上略微呈現(xiàn)出隨車速提高先降低后增長的趨勢。此外，由于本文鋼筋強度等級為 Q235，其屈服強度為 235 MPa，因此，在公交車36、54、72 km/h 三種車速情況下，鋼筋拉應力遠低于其屈服強度，均滿足正常使用要求。

圖19 鋼筋軸向應力時程曲線

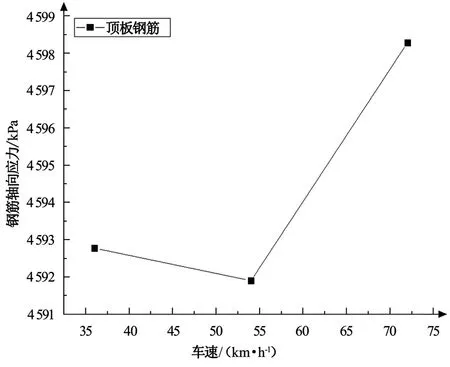
圖20 不同車速下的鋼筋軸向應力

4 結語

本文以某城市既有淺埋電力隧道為例，結合隧道區(qū)域地質狀況、隧道及道路設計資料，建立“公交車荷載-道路-電力隧道”三維耦合動力分析模型，研究分析了公交車在 36、54、72 km/h 三種不同車速下對電力隧道及道路結構產生的激勵效應和影響規(guī)律，結論如下。

1）隨著公交車車速的提高，路面和隧道頂板的振動效應總體上呈現(xiàn)出增大的趨勢，其中，最大沉降量和最大振動應力幅值隨車速變化的幅度較小，最大振動速度幅值和最大振動加速度幅值隨車速變化的幅度較大，路面最大振動加速度幅值出現(xiàn)在車速 54 km/h 時，而隧道頂板最大振動加速度幅值出現(xiàn)在車速 72 km/h 時。

2）在公交車 36、54、72 k m/h 三種車速情況下，隧道頂板最大拉應力幅值為 792.446、792.725、793.629 kPa，分別達到其抗拉強度的 44.52 %、44.54 %和 44.59 %，均滿足正常使用要求。

3）在公交車 36、54、72 km/h 三種車速情況下，鋼筋最大拉應力幅值為 4 592.778、4 591.907、4 598.286kPa，遠低于其屈服強度，均滿足正常使用要求。

針對路面和電力隧道在公交車移動荷載下的動力響應情況，建議如下。

1）加強對電力隧道周邊土體及道路的填筑質量的檢測與監(jiān)測，避免周邊土體及道路出現(xiàn)壓實度過低或松散現(xiàn)象，導致電力隧道結構振動響應過大出現(xiàn)結構破壞。

2）在進行磚混電力隧道建設時，應盡量采用預應力鋼筋混凝土預制板，以充分發(fā)揮鋼筋材料的抗拉性能，降低受拉區(qū)混凝土拉應力。