概率計算中數據思維的應用
陳壽文
概率計算中數據思維的應用
陳壽文
(滁州學院 數學與金融學院,安徽 滁州 239000)
概率計算是概率統計理論的重要組成部分.針對傳統概率統計教學重知識傳授輕數據思維引導現象,闡述了古典模型、全概率、獨立和事件、小概率事件、條件概率和幾何模型等概率計算中如何應用數據思維進行分析.教學實踐表明,運用數據思維的整體性、量化性、互聯性、價值性、動態性和圖像化等特征來計算概率,可以降低概率計算的復雜度,有利于理解隨機試驗過程和發現概率潛藏價值,還能夠促進學生數據思維意識形成和數據分析技能提升.
概率計算;數據思維;課程教學
概率統計是推動數據科學與大數據技術發展的主干學科.概率計算是概率統計理論的重要組成部分.數據驅動價值和數據思維成為大數據時代人們思考問題、解決問題的重要手段[1].傳統的概率統計教學過程往往只關注理論傳授和學生邏輯思維能力的培養,而忽視了內容的實際應用以及學生數據思維的訓練,致使學生盡管掌握大量的定義、定理和公式,在問題分析求解中卻不會運用[2],理論與實踐脫節,影響了實際教學效果和人才培養質量.本文運用數據思維對古典模型、全概率、獨立和事件、小概率事件、條件概率和幾何模型等概率計算進行教學探討,以期培育學生數據思維意識和數據分析技能.
1 概率計算方法與數據思維
概率計算需要不斷探索和實踐,理解事件的概率模型有助于求解概率問題.概率計算主要包括古典模型、幾何模型、全概率和條件概率的相關計算.古典模型的概率(古典概率)計算可分三步:確定所研究的對象為古典模型、計算樣本點數以及利用公式計算概率[3];幾何模型的概率(幾何概率)是一種“無限等可能”的概率模型,可借助幾何圖形(線段長度等)的測度計算概率[4];利用全概率公式可求得復雜事件的概率,關鍵在于找到適當的完備事件組對樣本空間進行分割[5];條件概率利用在已知信息限定的條件下研究事件發生的可能性,由它可推出全概率公式和貝葉斯公式.
數據思維是一種基于多源異構和跨域關聯的海量數據分析產生的數據價值挖掘思維,是收集、生產、處理數據,發現數據價值,并用數據來觀察世界、思考問題、分析問題、解決問題的一種量化思維模式,呈現出整體性、量化性、互聯性、價值性、動態性和圖像化等特征.一方面,運用數據思維特征計算概率,利于降低概率計算的復雜度;另一方面,計算概率過程中有意識地培養數據敏感度,發現數據的隱藏信息,利于促進數據思維的形成.
2 概率計算中數據思維的應用
為了引導學生用數據思維解決概率計算問題,提升其專業素養和數據分析能力,列舉以下計算情形.
2.1 古典概率計算中利用數據思維的整體性特征
數據思維主要特征為整體性.窮舉古典模型隨機試驗所有結果,將其作為整體,統計所關注試驗結果中包含的樣本個數,利用公式即可計算概率.
例1 彩票36選6+1方案:不考慮號碼順序,從號碼1~36中選出6個基本號,再從剩下的30個號碼中選出1個特別號,各個獎項的號碼分布及其獎金見表1.計算中獎概率并判斷購買彩票的收益情況.
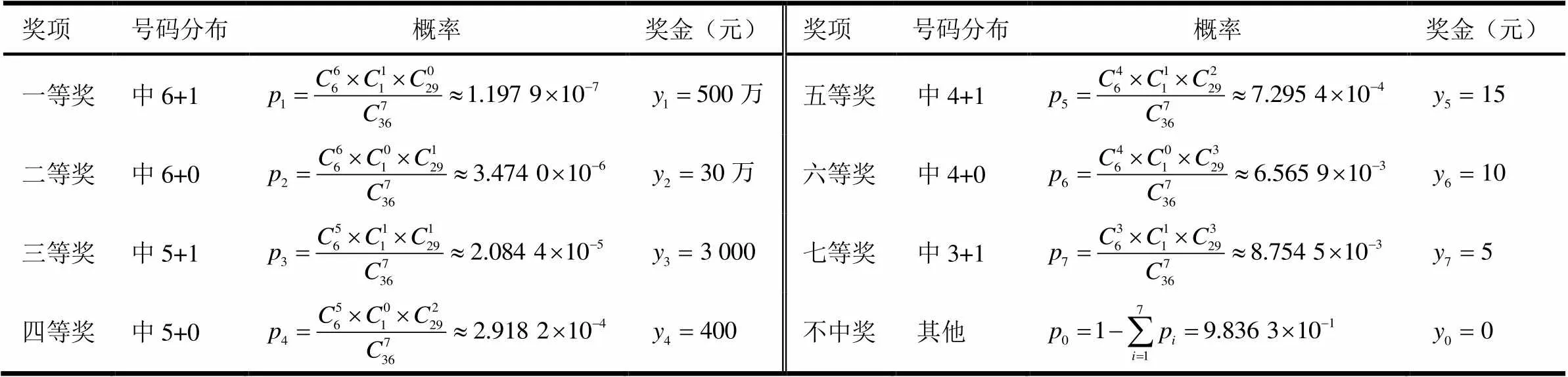
表1 彩票36選6+1方案的獎項及其概率分布
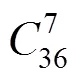
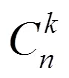
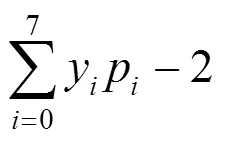
2.2 全概率計算中利用數據思維的量化性特征
數據思維表現出量化性特征.量化是具體或明確目標的一種表達,是解釋客觀世界的一種有效方式.其中,概率樹圖[6]是一種描述隨機試驗過程的工具.
例2 有兩只碗,碗1中裝有5粒綠豆和3粒紅豆,碗2中綠豆和紅豆數量分別為1粒和4粒.試驗中,先從兩碗中隨機抽取一只,接著在該碗中任意抽取一粒豆,試求取得綠豆和紅豆的概率.
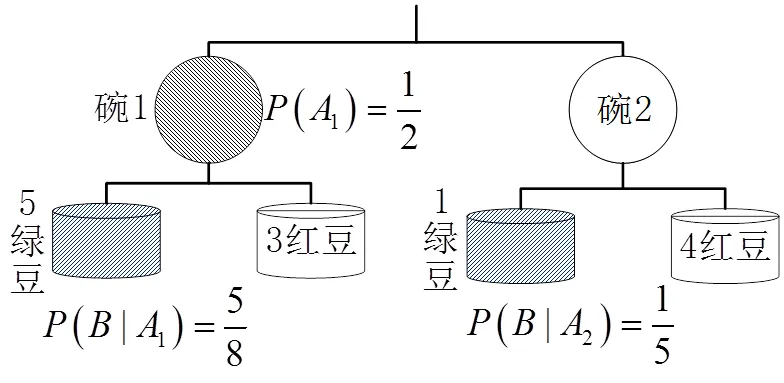
圖1 概率樹
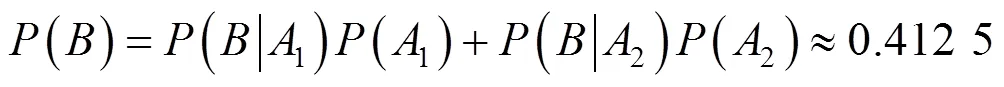
從數據可視化角度來看,利用概率樹圖展示隨機試驗的數據特征,增強了試驗過程的可理解性,數形合一,較傳統的計算概率方法,降低了計算難度.
2.3 獨立和事件概率計算中利用數據思維的互聯性特征
數據思維的互聯性源于事物泛在的相關關系.運用互聯思維可以發現不同事物之間的關聯,同樣在概率計算中,也可以運用互聯思維來挖掘概率潛藏規則.
例3 “三個臭皮匠,賽過諸葛亮”的數量化解釋.
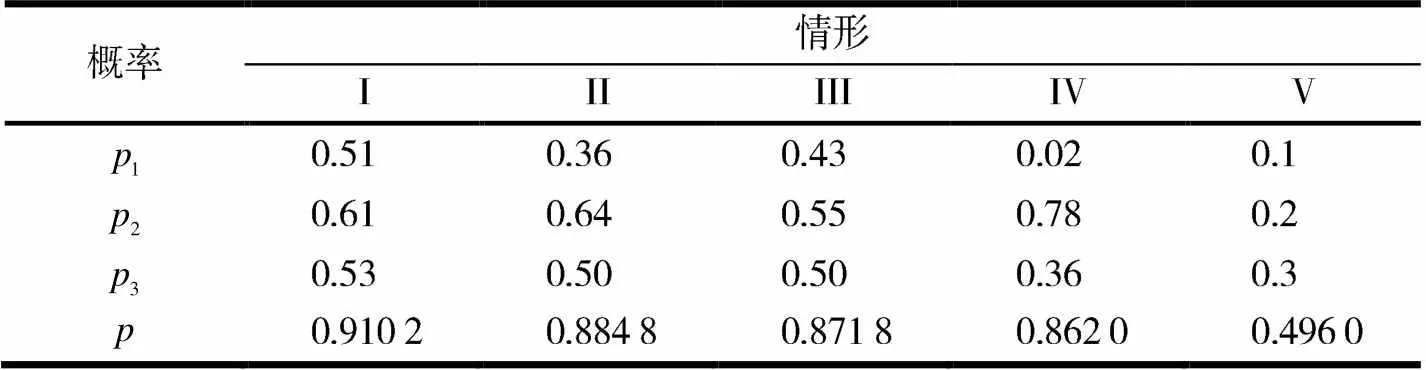
表2 五種情形下的數量化解釋
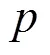
2.4 小概率事件概率計算中體會數據驅動決策的價值性
數據思維具有價值化特征,發掘數據潛藏價值是數據思維的本質,體現著大數據發展的直接目的.運用數據思維,能夠高效地處理數據分析任務,并對事件做出概率性的分析結果和預測.通過計算概率,基于“小概率事件在一次試驗中一般是不可能發生的”小概率事件原理來做推斷,啟發了人們的數據思維及思考模式.在對數據進行收集、整理和分析后,從中獲得洞察力,基于數據驅動決策,以支持決策具有更高的準確性,這體現著數據思維的價值性特點.
例4 大學英語四級考試包括聽力、語法結構、閱讀理解、綜合填空、寫作等,其中85分為單項選擇題,寫作15分.少數學生認為碰運氣有可能猜對選擇題.試從概率角度考察靠運氣能否通過英語四級考試.
分析 小概率事件原理是概率論中利用概率進行統計推斷的理論基石.單選題作答時從四個選項中隨機挑選一項,通過計算答題結果中不同答對數量發生的可能性大小,結合小概率事件原理來做推斷.
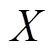
function t = tongguolv()
t=0;
for k=51:85
t = t + nchoosek(85,k)*0.25^k*0.75^(85-k);
end
sprintf('t=%f ',t);
end
2.5 條件概率計算中運用動態思維發現數據價值
數據思維擺脫了靜態思維的束縛,從動態視角來認識數據的價值.結合歷史數據記錄,運用樸素貝葉斯分類方法[7],依據最大后驗概率準則,可對動態數據記錄實施分類.
例5 商店購物數據庫中顧客表的部分記錄見表3,利用樸素貝葉斯分類方法分析零售數據.

表3 是否購買兒童早教機的顧客樣本
注: 該表在數據庫中被命名為“ZDJ”; 數據預處理(如年齡分段:18~44周歲為青年等)后,表中顧客編號為整數類型,其他字段均為字符串.
分析 樸素貝葉斯分類方法能夠基于客戶數據,識別出潛在顧客,這利于實現精準營銷,降低商業成本并增加企業利潤.
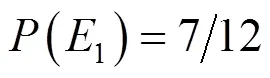
select (select count(*)from ZDJ where 類別 = '是' )/(select count(*)from ZDJ)
2.6 幾何概率計算中運用圖像展現數據的思維
在數據思維的應用中,通過數據的圖像化展現,可以使數據處理的目的和數據分析結論更易于被理解.
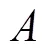
分析 幾何概率[9]計算需要確定樣本點和樣本空間所在的區域,從等可能參數值的含義入手,先找出相應的區域并確定它們的測度,再代入幾何概率公式來求解.
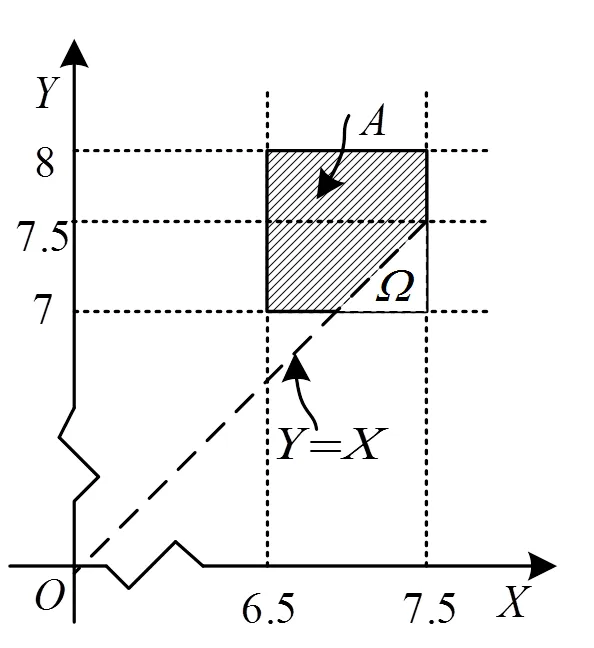
圖2 圖解隨機事件
3 結語
大數據時代,以數據的深度挖掘和融合應用為主要特征的智能化進程不斷被推演,培養本科生數據思維的重要性日益凸顯,專業學習應與數字化轉型、工業數字化戰略、人工智能發展規劃相結合,概率計算中尚需采用更多新措施去培養大學生的數據分析思維.
[1] 胡廣偉.數據思維[M].北京:清華大學出版社,2020:24-44.
[2] 石凱,劉洪江.地方高等院校概率統計課程教學改革模式探析[J].大學教育,2022(10):127-130.
[3] 曾宏偉.古典概型的概率計算方法與應用[J].信陽農業高等專科學校學報,2005,15(4):91-93.
[4] 段克峰.幾何概率的計算技巧與應用[J].甘肅聯合大學學報(自然科學版),2010,24(6):32-35.
[5] 李佳炎,張玉婷.全概率公式在復雜事件概率計算中的應用[J].中學數學研究,2023(1):35-38.
[6] 王榮.用概率樹圖法求解事件發生的概率[J].天津成人高等學校聯合學報,2004,6(5):18-20.
[7] 張步良.基于分類概率加權的樸素貝葉斯分類方法[J].重慶理工大學學報(自然科學版),2012,26(7):81-83.
[8] 韓兵,王照清,廖聯軍.基于MySQL多表分頁查詢優化技術[J].計算機系統應用,2016,25(8):171-175.
[9] 劉崇林.幾何概率計算中參數及測度的選取[J].中學數學雜志,2010(5):28-30.
[10] 王靜.量子蒙特卡洛方法的發展與應用[D].上海:華東師范大學,2022.
Application of data thinking in probability calculation
CHEN Shouwen
(School of Mathematics and Finance,Chuzhou University,Chuzhou 239000,China)
Probability calculation is an important component of probability statistics theory.In view of the phenomenon that traditional probability and statistics teaching pays more attention to knowledge teaching than data thinking guidance,it is explored that how to apply data thinking in probability calculations such as classical models,total probability,independent sum events,small probability events,conditional probability and geometric models.Teaching practice has shown that,using the holistic,quantitative,interconnected,valuable,dynamic,and visual characteristics of data thinking to calculate probability,the complexity of probability calculation can be reduced,the process of random experiments is beneficial to being understanded,and the hidden value of probability is conducive to being discovered and it can also promote the formation of students′ data thinking awareness and the improvement of data analysis skills.
probability calculation;data thinking;course teaching
O211∶G642.0
A
10.3969/j.issn.1007-9831.2024.02.016
2023-08-01
安徽省高校質量工程項目(2020jyxm1353,2021kcszsfkc292);滁州學院質量工程項目(2019jyz011,2020kcsz022)
陳壽文(1979-),男,安徽懷寧人,副教授,博士,從事統計學研究.E-mail: cshouwen@163.com

