Effective dynamics for a spin-1/2 particle constrained to a curved layer with inhomogeneous thickness

Guo-Hua Liang(梁國(guó)華) and Pei-Lin Yin(尹佩林)

School of Science,Nanjing University of Posts and Telecommunications,Nanjing 210023,China

Keywords: curved surface,inhomogeneous thickness,spin-1/2 particle,effective Hamiltonian

1.Introduction

Research of quantum motion in curved spacetime is a fundamental and captivating subject in physics, particularly when examining quantum phenomena occurring in the early universe and near black holes.Although astronomical observations provide valuable insights, experimental investigations on the effects of such large curvature are seemingly impossible.However, with advancements in micro and nanofabrication technology, laboratories are now able to manufacture nanostructures with various geometries.[1–5]Some of these low-dimensional nanostructures exhibit significant curvature,offering excellent platforms for studying the impact of curvature on quantum particles.With the aid of analog models,experiments involving different dynamics on a curved surface are expected to shed light on how space curvature influences the corresponding evolution processes.Optical experiments,for instance, have observed curvature effects on the correlation length of a beam,[6]the phase and group velocities of a wavepacket[7]and speckle patterns.[8]In the realm of quantum many-body systems, the observation of ultracold atomic bubbles[9]and Bose–Einstein condensate[10]in shell-shaped gases has been achieved.

Theoretically, the thin-layer procedure (TLP) was introduced as an appropriate method to describe the quantum dynamics on a curved surface.[11,12]This method naturally incorporates a scalar potential determined by the surface curvature in the effective two-dimensional (2D) equation, which is known as the geometric potential.Subsequently, the predicted potential was experimentally demonstrated in photonic crystals.[13]The geometric potential is attractive and leads to the formation of bound states, opening up new possibilities for constructing quantum dots[14,15]and quantum waveguides.[16–18]Inspired by these applications,numerous researchers have extended this method to other scenarios, including a charge particle in electric and magnetic fields,[19–21]a Dirac particle,[22–24]a spin-1/2 particle,[25–30]higher-dimensional induced gauge potential,[31–35]quantum scattering,[36]photons,[37–39]magnetism,[40,41]and quantum many-body systems.[42,43]It has been revealed that the effective dynamics exhibit additional geometric effects associated with the internal degrees of freedom and properties of the confined particle.Specifically,for spin-1/2 particles,the curvature induces pseudo-magnetic fields and effective spin–orbit interactions.

Most studies on the effective dynamics on curved surfaces have focused on motions within a thin layer of constant thickness, assuming that the ground state in the normal direction is independent of the surface coordinates.However, in reality, it is inevitable for low-dimensional structures to have an inhomogeneous thickness.Therefore, it is necessary to develop theoretical approaches that take into account the effect of varying thickness.In a previous work,[44]we extended TLP and derived the effective dynamics for a scalar particle confined to a curved surface with inhomogeneous thickness.It is found that the inhomogeneous confinement could induce an effective potential which is determined by the morphology of the thickness function, and is proportional to the ground state energy.This raises questions regarding spin-1/2 particles: Does the varying thickness induce additional spin–orbit interaction? Is the spin-dependent process affected by thickness fluctuations?Here,the extra spin–orbit interaction is supposed to be originated from the spin connection which can be viewed as anSU(2) gauge field generated by local Lorentz transformation.[45]With this study we wish to clarify the problems and give the explicit Hamiltonian for a spin-1/2 particle constrained to a curved surface with inhomogeneous thickness.

The article is organized as follows.In Section 2, we derive the effective Hamiltonian for a spin-1/2 particle constrained to an arbitrary curved surface by an inhomogeneous confinement.Then we discuss the case of asymmetric confining potential in Section 3 and summarize our result in Section 4.

2.Effective dynamics

A curved surfaceSin three-dimensional(3D)Euclidean space can be described by a position vectorr(q1,q2), where(q1,q2)are the curvilinear coordinates,as illustrated in Fig.1.We assume that a spin-1/2 particle is bounded to a thin layer with varying thickness by a confining potentialVc.The thickness of the layer is symmetric aboutS.Considering the inhomogeneity of the thickness, we use the adapted coordinate system (q1,q2,Q3) to parameterize the portion of space nearS,

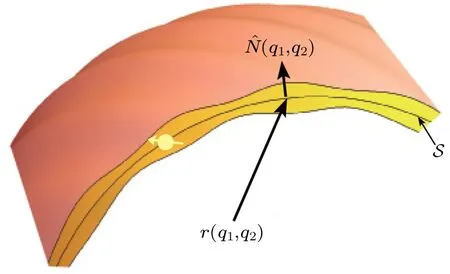
Fig.1.Schematic diagram of a curved thin-layer with inhomogeneous thickness.Surface S is in the middle of the layer.A spin-1/2 particle is confined to the layer(yellow region).

To constrain the particle toS, the confining potentialVcshould have a deep minimum at the surface(Q3=0),thus being expanded as a power series inQ3,

andgab=?ar·?bris the 2D metric tensor for the surfaceS.Here, ?GABcorresponds to the case of constant thickness,whileKABis obviously originated from the thickness fluctuation.The determinant ofGABis found to beG=|γ|/s.

It is also necessary to deduce the exact form of the inverse of the metric tensor,which turns out to be

In Eq.(20),H0describes a particle bounded by the harmonic oscillator potential in the transverse direction and takes a lead role inH,whileH1+H′1seemingly gives the quantum dynamics in the tangential direction onS.Specifically,H′1arises from the variation in thickness, a term not observed in the case of constant thickness.To get the effective 2D Hamiltonian we must separate the wavefunction in the Schr?dinger equationHΨ=EΨ,whereEdenotes the total energy.In this paper,we focus on the energy range where the state in the normal direction is always the ground state.Making the ansatzΨ=∑β uβ(q1,q2)χβ(Q3), whereβlabels the spin degeneracy forH0,we obtain

whereE1=E-E0.Note thatE0in Eq.(24) is of the order 1/ε,which is supposed to be the ground state energy and also the dominant part of the total energyE.Equation (25) describes the 2D effective dynamics onSunder the transverse mode energyE0.Taking into accountE0～ε-1in Eq.(25),we must keep (s-1)～ε, which gives the application range of our method.

As the spin degeneracy, the effective 2D Hamiltonian should be a 2×2 matrix,with the elements

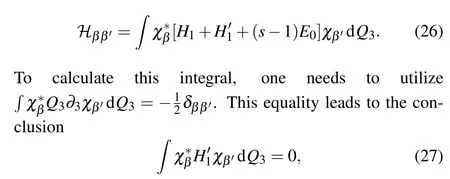
indicating that, to the order ofε0, the thickness variation of curved thin-layer does not give rise to an extra spin–orbit interaction in the 2D effective Hamiltonian.It should be noted that,although no physical effect exhibits from the 2D information,the combination of curvature and thickness gradient does result in a non-zero spin connection component ˉ?3,which may affect the spin density distribution in the direction of thickness.

Performing the integral in Eq.(26)we eventually find that the effective Hamiltonian matrix is diagonal and the explicit form is

In this effective Hamiltonian,Vgand(s-1)E0are two scalar potentials, which are due to the surface curvature and the thickness variation, respectively.Compared to the geometric potentialVg, the effective potential (s-1)E0depends on the ground state energy in the normal direction of the surface.It has been clarified that ˉ?acontained in the gauge derivative is composed of?aandAso, which lead to the pseudo-magnetic field with intensityKand the effective spin–orbit interaction with coupling tensor determined by the Weingarten matrix.

A key conclusion we draw here is that the thickness variation of the curved thin-layer does not bring an extra spin–orbit interaction in the effective dynamics.The reason for this is that obtaining the 2D tangential dynamics requires freezing and integrating the state perpendicular to the surface, which inherently neutralizes the detailed information in the thickness direction.This conclusion suggests that,despite the scalar potential (s-1)E0, the energy splitting dependent on spin remains unaffected by thickness imperfection in thin-layer systems with arbitrary geometries, highlighting the reliability of spin interference measurements in relevant experiments.

3.Asymmetric confinement

The effective Hamiltonian (28) is obtained under the condition of symmetric confinement in the normal direction,namelyVc(Q3) is an even function.In reality, many 2D systems are under the confining potential with inversion asymmetry.In the following,we study the case of asymmetric confinement to figure out whether the Hamiltonian(28)is still applicable.The system to be considered is shown in Fig.2(a),with the modification that one of the layer side is a hard-wall potential[see Fig.2(b)], which could totally reflect the wave function.The corresponding confining potential can be expressed as

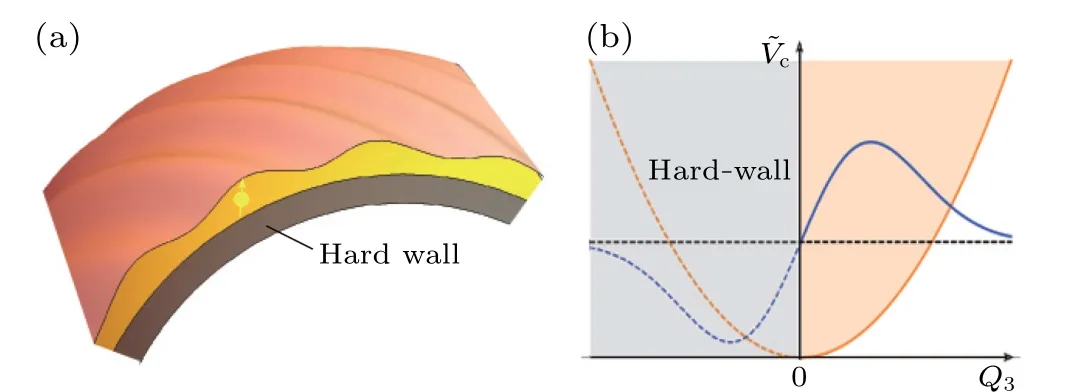
Fig.2.(a) Schematic picture of a curved thin-layer with asymmetric confinement.One side is the same as Fig.1 and the other side is a hardwall potential.(b)The confining potential and bound state as a function of Q3.The dashed lines correspond to the symmetric confinement.

The Hamiltonian(20)still holds in this condition after replacing the confining potential in Eq.(21).As before,we make the assumptionΨ=∑β uβ(q1,q2)ˉχβ(Q3), where ˉχ(here we ignore the degenerate index)satisfies the 1D equation

4.Conclusion

In conclusion, we obtain an effective Hamiltonian for a spin-1/2 particle constrained to an arbitrary curved thin layer with varying thickness by using the confining potential approach.It is shown that the pseudo-magnetic field and effective spin–orbit interaction of constant thickness case are still applicable and thickness variation does not lead to an extra spin–orbit interaction.This result implies a robustness of spin-dependent energy splitting to the thickness fluctuations in curved thin-layer systems.Our result is also proved to be valid for both symmetric and asymmetric confinement cases.The latter can be utilized to describe one-side etching structures, which are more common in fabrication of waveguides and metamaterials.By providing a theoretical tool, this effective Hamiltonian allows for a quick assessment of the geometric effects on properties of low-dimensional nanostructures and aids in design processes.

Appendix A: Calculation details in the separation of dynamics

Acknowledgments

This work was supported in part by the National Natural Science Foundation of China (Grant No.12104239),National Natural Science Foundation of Jiangsu Province of China (Grant No.BK20210581), Nanjing University of Posts and Telecommunications Science Foundation (Grant Nos.NY221024 and NY221100), the Science and Technology Program of Guangxi, China (Grant No.2018AD19310),and the Jiangxi Provincial Natural Science Foundation(Grant No.20224BAB211020).